Корни квадратного уравнения независимые случайные величины

Какова вероятность того, что корни этого уравнения будут действительными числами?

Коэффициенты р и q квадратного уравнения х 2 + рх + q = 0 выбирают наудачу на отрезке [0; 2]. Какова вероятность того, что корни этого уравнения будут действительными числами?

Решение. Обозначим событие: А – корни данного уравнения бу­дут действительными числами. Найдем вероятность события А, применив формулу р(А) = mesD / mesΩ. Пусть коэффициенты р и q квадратного уравнения ‒ наудачу взятые числа. Их воз­можные значения: 0 2 – 4q > 0, откуда следует, что q ≤ р 2 / 4.

Построим границы области, которой принадлежат точки плоскости, удовлетворяющие условиям:

Граничные прямые р = 0, р = 2, q = 0, q = 2 являются сторонами квадрата, ограничивающего область возможных значений р и q. Граничная кривая q = р 2 /4 представляет собой параболу. Решениями состав­ленной системы неравенств являются координа-ты всех точек плоскости, расположенных на рис. 1.14 заштрихованной области, то есть между граничными линиями р = 0, q = 2, q = р 2 /4 и на самих этих линиях. Точки плоскости, принадлежащие заштрихованной области, характеризуют исхо­ды испытания, благоприятст-вующие событию А. Площадь заштрихованной области равна

Таким образом, вероятность события А равна р(А) = S_g / S_G = 1 / 6.

Случайное квадратное уравнение

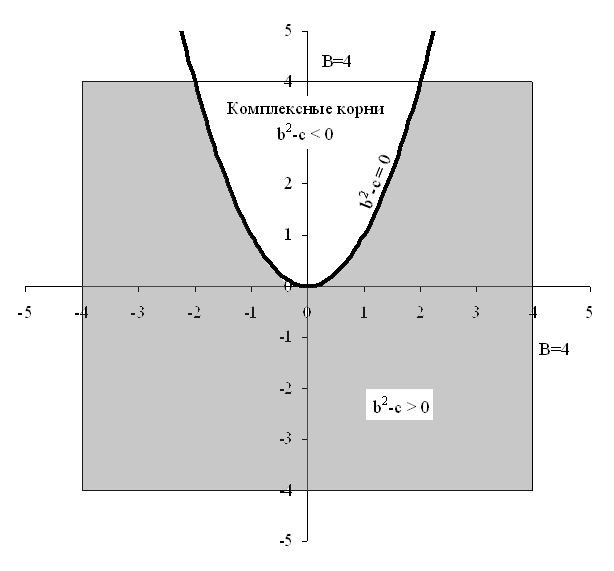
Какова вероятность того, что корни квадратного уравнения x 2 + 2bx + c = 0 вещественны?

Для того чтобы вопрос задачи имел смысл, предположим, что точка (b, c) равномерно распределена на квадрате с центром в начале координат и стороной 2B (рис. 1). Решим задачу при фиксированном B, а затем устремим B к бесконечности, так что b и c могут принимать любые значения.

Рис. 1. Серая область отвечает случаю вещественных корней

Для того чтобы уравнение имело вещественные корни, необходимо и достаточно, чтобы
b 2 — c ≥ 0.

На приведенном рисунке изображена парабола b 2 = c и показана область, где наше уравнение имеет вещественные корни для B = 4.

Нетрудно подсчитать, что площадь незаштрихованной области равна 4/3∙B 3/2 (при B ≥ 1), а площадь всего квадрата, конечно, равна 4B 2 . Следовательно, вероятность того, что корни комплексные, равна 1/3∙√ B . При B = 4 ответ равен 1/6. С ростом B 1/√ B стремится к нулю, так что вероятность того, что корни вещественные, стремится к 1.

Следует заметить, что эта задача отличается от такой же задачи, связанной с уравнением ax 2 + 2bx + c = 0. Конечно, можно разделить на a, но если a, b и c были независимы и равномерно распределены в некотором кубе, то b/a и c/a уже зависимы и распределены неравномерно.

Публикуется по работе: Пятьдесят занимательных вероятностных задач с решениями. Ф.Мостеллер, перев. с англ., издание второе. М. Наука, 1975, 112 с.

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди «Не укради»

Нахождение законов распределения двумерных случайных величин

Найти условный закон распределения случайной величины Х, при условии Y=4, если закон распределения двумерной дискретной случайной величины представлен таблицей 11. Являются ли величины Х и Y независимыми?

Таблица 11 – Закон распределения случайной величины (Х,Y)

Найдём безусловные законы распределения случайных величин Х и Y. Для этого, дополним таблицу 11 столбцом и строкой, в которой будем находить суммы вероятностей соответственно в строках и в столбцах (см. таблицу 5). Получим таблицу 12.

Таблица 12 – Отыскание безусловных вероятностей случайных величин Х и Y по данным задачи 2.6.1

Безусловные законы распределения случайных величин Х и Y оформим в виде таблиц (таблицы 13 и 14 соответственно).

Таблица 13 – Безусловный закон распределения случайной величины Х

Таблица 14 – Безусловный закон распределения случайной величины Y

Используя обозначения таблиц 5 и 6, а также формулу (39), найдём :

При этом выполняется

Условный закон распределения случайной величины Х, при условии Y = 4, можно представить таблицей 15.

Таблица 15 – Закон распределения случайной величины Х/(Y = 4) к задаче 2.6.1

Х	0,1	0,2	0,3

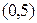Сравним вероятности значений случайной величины X в условном (табл. 15) и безусловном (табл. 13) законах распределения. Если бы величины Х и Y были независимы, распределение величины X не зависело бы от условий, а вероятности в обоих законах были бы одними и теми же.

Таким образом, сравнивая законы, можно сделать вывод о наличии зависимости между величинами Х и Y.

Замечание: в случае, если условный закон распределения Х при некотором условии совпадёт с её безусловным законом распределения, вывод о независимости величин Х и Y сделать будет нельзя: потребуется проверка всех остальных условий.

Ответ: условный закон распределения случайной величины Х, при условии Y=4, представлен в таблице 15; величины Х и Y зависимы.

Найти плотности распределения величин Х и Y, если известна их совместная плотность распределения (плотность распределения двумерной случайной величины (Х и Y)):

Используя формулы (41) и (42), а также с учётом условий: , получим:

Ответ: плотности распределения величин Х и Y соответственно равны и

СПИСОК РЕКОМЕНДУЕМЫХ ИСТОЧНИКОВ

1 Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст]: учебное пособие / В.Е. Гмурман. — М.: Высшее образование, 2010. — 479 с.

2 Гнеденко, Б.В. Курс теории вероятностей [Текст]: учебное пособие / Б.В.Гнеденко. — М.: Издательская группа URSS, 2001. — 320 с.

3 Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике [Текст]: учебное пособие / В.Е. Гмурман. — М.: Юрайт, 2010. — 404 с

4 Вентцель, Е.С. Задачи и упражнения по теория вероятностей [Текст]: учебное пособие / Е.С. Вентцель, Л.А. Овчаров. — М.: Кнорус, 2010. — 480 с.

5 Ивашев-Мусатов, О.С. Теория вероятностей и математическая статистика [Текст]: учебное пособие / О.С. Ивашев-Мусатов. — М.: Издательская группа URSS, 2003. — 224 с.

Интернет-ресурсы

Перечень интернет-ресурсов по теории вероятностей и математической статистике [Электронный ресурс] / Режим доступа: http://zyurvas.narod.ru/resursy.html.

Полный курс лекций по Теории вероятностей [Электронный ресурс]/ НГУ, ред. Н.И. Чернова. – Режим доступа: http://www.nsu.ru/mmf/tvims/chernova/tv99.html.

Готовый учебник по теории вероятностей на русском и английском языках, подготовлен группой ученых ОФИМ СО РАН, интеракивный режим работы, подсказки. – Режим доступа: http://newasp.omskreg.ru/probability.

Сотникова, Н.Я. Первоапрельский задачник по теории вероятностей для студентов нематематиков [Электронный ресурс]/ Режим доступа: http://www.astro.spbu.ru/staff/nsot/Teaching/tver/zadachi.html.

Манита, А.Д. Теория вероятностей и математическая статистика [Электронный ресурс]/ электронная версия учебника. – Режим доступа: http://teorver-online.narod.ru.

ПРИЛОЖЕНИЕ А. Варианты заданий для контрольной работы

1.1 Известно, что события А и В произошли, а событие С не произошло. Определите, произошло или нет событие .

1.2 На шести карточках написаны буквы «А», «А», «Б», «Б», «Б», «О». Какова вероятность того, что расположенные в ряд наудачу эти карточки составят слово «БАОБАБ»?

1.3 Из урны, в которой находятся десять красных и пять синих шаров, наугад вынимаются три шара. Какой состав шаров по цвету извлечь наиболее вероятно?

1.4 Из интервала [1; 3] наугад выбираются 2 вещественных числа. Найти вероятность того, что их сумма больше 5.

1.5 Известно, что 96% выпускаемых деталей удовлетворяют стандарту. При упрощенном контроле стандартная деталь признается стандартной с вероятностью 98%, а бракованная деталь признается стандартной с вероятностью 5%. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.

1.6 В урне находятся 10 шаров, среди которых половина черных, а остальные белые. 10 раз производится случайная выборка шара из урны с возвратом. Рассчитать вероятность того, что ровно 5 раз был выбран черный шар.

1.7 В партии из 6 деталей имеется 4 стандартные. Наудачу отобраны 3 детали. Составить закон распределения дискретной случайной величины Х – числа стандартных деталей среди отобранных. Найти математическое ожидание и дисперсию случайной величины Х.

1.8 Система (X,Y) имеет плотность распределения , если и , в остальных случаях 0. Найти функцию распределения и вероятность попадания случайной точки (x, y) в прямоугольник , .

2.1 Докажите, что для событий А и В выполняется равенство .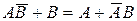

2.2 На шахматную доску произвольным образом поставили две ладьи. Какова вероятность того, что ладьи находятся под ударом друг друга?

2.3 Восемь команд спортсменов разбиваются случайным образом на две группы по четыре команды в каждой группе. Найти вероятность того, что две наиболее сильные команды окажутся в одной группе.

2.4 Определить вероятность того, что корни квадратного уравнения x 2 +2ax+b = 0 являются вещественными, если коэффициенты a и b выбираются наугад из интервала от 0 до 1.

2.5 В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,95. Для винтовки без прицела вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведёт один выстрел из наудачу взятой винтовки.

2.6 Вероятность брака равна 0,01. Найти вероятность того, что среди 200 деталей не более двух бракованных.

2.7 Найти дисперсию и среднее квадратичное отклонение случайной величины Х, заданной законом распределения:

2.8 Независимые случайные величины Х и Y равномерно распределены на промежутках и соответственно. Найти их плотности распределения и , функции распределения и , совместную плотность распределения .

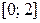
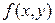
3.1 Докажите, что для событий А и В выполняется равенство .

3.2 Вероятность отказа каждого прибора при испытании равна 1%. Сколько таких приборов надо испытать, чтобы с вероятностью не менее 90% получить хотя бы один отказ?

3.3 Из колоды карт (52 листа) наудачу извлекаются три карты. Найти вероятность того, что будут вынуты последовательно тройка, семерка и туз.

3.4 В точке С, положение которой на телефонной линии АВ длины L равновозможно, произошёл разрыв. Определить вероятность того, что точка С удалена от точки А на расстояние, не меньшее l (l