Корни квадратного уравнения отрицательные числа

Корни квадратного уравнения отрицательные числа

Из содержания предыдущих уроков можно сделать вывод: для развития алгебры отправными точками были, во-первых, использование удобной символики, а во-вторых, операции с отрицательными числами (или, если угодно, величинами). Введение отрицательных чисел помогало свести множество различных частных случаев к общему правилу. Но в то же время отрицательные числа составляли и определенную проблему: они не наглядны, и непонятно, как обосновать действия с ними. Прежде всего, неясно, что за объекты им соответствуют. Постепенное введение отрицательных чисел в математику поэтому должно было состоять, с одной стороны, в развитии операций с этими числами, а с другой стороны – в уяснении их природы.

На «западной» почве (точнее говоря, в эллинистическом Египте) введение отрицательных величин впервые произошло у Диофанта. Он даже использовал специальный символ для них (сейчас мы в этом качестве используем знак «минус»). Правда, ученые спорят, обозначал ли символ Диофанта именно отрицательное число или просто операцию вычитания, потому что у Диофанта отрицательные числа не встречаются изолированно, а только в виде разностей положительных; и в качестве ответов в задачах он рассматривает только рациональные положительные числа. Но в то же время Диофант употребляет такие обороты речи, как «Прибавим к обеим сторонам отрицательное», и даже формулирует правило знаков: «Отрицательное, умноженное на отрицательное, дает положительное, тогда как отрицательное, умноженное на положительное, дает отрицательное» (то, что сейчас обычно формулируют: «Минус на минус дает плюс, минус на плюс дает минус»).

Термин «лейпсис», используемый Диофантом для отрицательного числа, дословно означает «нехватка», «отсутствие», в то время как термин «гюпарксис» (положительное число) значит «существование», «достояние», «имущество»: получается, что отрицательное – то, чего в «имуществе» не хватает; это, возможно, связано с трактовкой отрицательного числа как задолженности.

Диофант жил в III в. н. э., а в Китае отрицательные числа использовались уже во II в. до н. э., а может быть, и раньше. Возникли они в связи с решением систем линейных уравнений, которым посвящена VIII книга трактата «Математика в девяти книгах» (его окончательная редакция которого относится ко II в. до н. э.). При сложении и вычитании уравнений для исключения неизвестных коэффициенты при тех или иных неизвестных нередко становились отрицательными. Китайцы выполняли преобразования этих систем уравнений на счетной доске, при этом числа выкладывали палочками. Для отрицательных чисел использовались палочки другого цвета или другой формы, чем для положительных (при записи для этого использовали другие чернила или же числа отмечались косой чертой). Отрицательные числа назывались «фу», а положительные – «чжэн». Существовали правила арифметических действий с числами «фу». Вначале эти числа, видимо, понимались как удобная фикция, которая позволяет применять один и тот же алгоритм вычитания уравнений друг из друга, не заботясь при этом о знаках коэффициентов. Впоследствии отрицательные числа стали интерпретироваться как задолженность, недостача.

Индийские математики используют отрицательные числа с VII в. н. э.: Брахмагупта сформулировал правила арифметических действий с ними и, как мы видели, применял их при рассмотрении квадратных уравнений. Магавира (IX в.) не только обсуждал два значения квадратного корня – положительное и отрицательное, но и ставил вопрос о возможности извлечения корня из отрицательного числа. При этом он пришел к отрицательному выводу: «Квадрат положительного или отрицательного – числа положительные. Так как отрицательное число по своей природе не является квадратом, то оно не имеет квадратного корня». Индийцы называли положительные числа «дхана» или «сва» (имущество), а отрицательные – «рина» или «кшайя» (долг). Впрочем, и в Индии с пониманием и принятием отрицательных чисел были связаны проблемы. Обсуждая двойное значение корня, Бхаскара (XII в.) писал: «Люди не одобряют отвлеченных отрицательных чисел».

В арабской математике отрицательные числа почти не нашли применения. В одном тесте математик Абу-л-Вафа (X в.) рассматривает умножение –2 на 10. Для отрицательного числа он использует слово «дайн» (долг): число –2 называется «долг два», а –20 – «долг двадцать». Позже некоторые европейские математики, например, Леонардо Пизанский (Фибоначчи, XIII в.), тоже будет использовать для отрицательных чисел термин «долг» (лат. debitum). Самаркандский математик XV в. Али Кушчи, бывший послом Улугбека при китайском императоре, «перевел» на арабский китайские термины «чжэн» и «фу» как «мусбат» и «манфи»; эти «мусбат» и «манфи» европейские математики, познакомившиеся с сочинением Али Кушчи благодаря византийцам, передали словами positivus и negativus (положительный и отрицательный), а также, иногда, affirmativus и privativus (утвердительный и «отнимательный»).

Хотя многие европейские математики эпохи Возрождения так или иначе пользовались отрицательными числами, их считали «ложными», «фиктивными», «мнимыми». Но, тем не менее, идея отрицательных чисел постепенно завоевывала умы и, главное, оказалась весьма полезной. Так, благодаря им удалось свести методы решений квадратных уравнений к одному случаю. В Индии это впервые произвел, как мы видели, еще Брахмагупта в VII в.; в Европе же это произошло в XVI в. в сочинении М. Штифеля «Полная арифметика», сведшего все квадратные уравнения к одному виду: в современных обозначениях, . При этом Штифель систематически изложил теорию операций с отрицательными числами. По поводу этих чисел он пишет: «Ты видишь, конечно, что все это с первого взгляда очень похоже на самый пустой вздор, и, однако же, выполненные в соответствии с этим алгебраические действия приводят к выражениям поистине удовлетворительным. Итак, подобно тому, как мы представляем себе различные числовые корни у чисел, не имеющих таких корней (т. е. иррациональные числа), и это представление оказывается в высшей степени полезным для математики, так же не без пользы представляем себе и число ниже 0, то есть ниже, чем ничего».

Почти одновременно со Штифелем защищал идею отрицательных чисел Р. Бомбелли, переоткрывший сочинение Диофанта. Бомбелли не только установил правила обращения с отрицательными числами, но и выдвинул идею использования квадратных корней из отрицательных чисел – это были бы особые числа (сейчас мы называем их комплексными числами), не положительные и не отрицательные, но при этом, как было показано, очень полезные для математики, в том числе для решения многих конкретных задач, связанных с действительными числами. Введение комплексных чисел также позволяет «унифицировать» множество различных случаев. Например, удобно считать, что любое квадратное уравнение всегда имеет решение: уравнения, дискриминант которых отрицателен и которые поэтому не имеют действительных корней, имеют, тем не менее, два комплексных, поскольку в множестве комплексных чисел всегда можно извлечь квадратный корень, даже из отрицательного числа.

Выражение «ниже, чем ничего» показывает, что Штифель и некоторые другие мысленно воображали положительные и отрицательные числа точками на вертикальной шкале (вроде шкалы термометра). Развитое затем математиком А. Жираром представление об отрицательных числах как о точках на некоторой прямой, располагающихся по другую сторону от нуля, чем положительные, оказалось решающим в обеспечении этим числам прав гражданства, особенно в результате развития метода координат у П. Ферма и Р. Декарта.

Некоторые математики все же пытались, подражая древним, строить науку без отрицательных количеств. Среди этих «консерваторов» был и Ф. Виет, открывший и обосновавший (на уравнениях степеней от второй до пятой) замечательный факт, ныне называемый теоремой Виета. В уравнении -ой степени с коэффициентом 1 при старшем члене коэффициенты при , , и т. д. суть взятые с чередующимися знаками суммы корней, пар корней, троек корней и т. д. В школе теорему Виета проходят для (впрочем, при этот факт был известен уже Дж. Кардано).

Так вот, Виет все это писал только для уравнений, все корни которых положительны. Скажем, для уравнения вида:

имеющего два положительных корня и один отрицательный, Виет, чтобы не рассматривать отрицательный корень , вместо равенств:

(эти формулы получаются из предыдущих, если заменить на –(), поскольку ).

Сам Декарт, называя отрицательные числа (например, корни уравнения) «ложными», все же именовал и положительные, и отрицательные числа «действительными» (reelles) в отличие от комплексных – «мнимых» (imaginaires).

Все же некоторые свойства отрицательных чисел долго оставались неясными, особенно отношения порядка (больше-меньше). Например, удивляло, что в пропорции

слева первый член больше второго, а справа меньше: получалось как будто бы, что большее отношение равно меньшему (это недоумение высказывал, в частности, А. Арно, друг Б. Паскаля и автор книги «Логика, или Искусство мыслить»). Споры о том, что же все таки представляют собой отрицательные числа, как обосновать правило знаков, по какому праву можно переносить правила арифметических действий с положительными числами на числа отрицательные, продолжались и в XVII, и в XVIII вв., что, однако, не мешало использованию этих чисел. Так, математик и философ д’Аламбер писал в середине XVIII в. в «Энциклопедии»: «Правила алгебраических действий с отрицательными количествами в общем приняты всеми и считаются точными независимо от того, что подразумевается под этими количествами».

Дискриминант

Дискриминантом квадратного трехчлена называют выражение \(b^<2>-4ac\), где \(a, b\) и \(c\) – коэффициенты данного трехчлена.

Например, для трехчлена \(3x^2+2x-7\), дискриминант будет равен \(2^2-4\cdot3\cdot(-7)=4+84=88\). А для трехчлена \(x^2-5x+11\), он будет равен \((-5)^2-4\cdot1\cdot11=25-44=-19\).

Дискриминант обозначается буквой \(D\) и часто используется при решении квадратных уравнений . Также по значению дискриминанта можно понять, как примерно выглядит график квадратичной функции (см. ниже).

Дискриминант и корни квадратного уравнения

Значение дискриминанта показывает количество корней квадратного уравнения:
— если \(D\) положителен – уравнение будет иметь два корня;
— если \(D\) равен нулю – только один корень;
— если \(D\) отрицателен – корней нет.

Это не надо учить, к такому выводу несложно прийти, просто зная, что квадратный корень из дискриминанта (то есть, \(\sqrt\) входит в формулу для вычисления корней квадратного уравнения: \(x_<1>=\) \(\frac<-b+\sqrt><2a>\) и \(x_<2>=\) \(\frac<-b-\sqrt><2a>\) . Давайте рассмотрим каждый случай подробнее.

Если дискриминант положителен

В этом случае корень из него – это некоторое положительное число, а значит \(x_<1>\) и \(x_<2>\) будут различны по значению, ведь в первой формуле \(\sqrt\) прибавляется, а во второй – вычитается. И мы имеем два разных корня.

Пример: Найдите корни уравнения \(x^2+2x-3=0\)
Решение:

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Найдем корни уравнения

Получили два различных корня из-за разных знаков перед \(\sqrt\)

На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение \(x^2+2x-3=0\) имеет корни \(x_<1>=1\) и \(x_<1>=-3\), значит при подстановке \(1\) и \(-3\) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию \(y=x^2+2x-3\) получим \(y=0\). То есть, функция \(y=x^2+2x-3\) проходит через точки \((1;0)\) и \((-3;0)\) (подробнее смотри статью Как построить график функции ).

Если дискриминант равен нулю

А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.

Формулы корней выглядят так: \(x_<1>=\) \(\frac<-b+\sqrt><2a>\) и \(x_<2>=\) \(\frac<-b-\sqrt><2a>\) . И если дискриминант – ноль, то и корень из него тоже ноль. Тогда получается:

То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.

Пример: Найдите корни уравнения \(x^2-4x+4=0\)
Решение:

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Находим корни уравнения

Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.

На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция \(y=x^2-4x+4\) будет выглядеть вот так:

Если дискриминант отрицателен

В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.

Пример: Найдите корни уравнения \(x^2+x+3=0\)
Решение

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Находим корни уравнения

Оба корня содержат невычислимое выражение \(\sqrt<-11>\), значит, и сами не вычислимы

То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение \(x^2+x+3\) получился ноль.

Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.

Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!

Решение квадратных уравнений с отрицательным дискриминантом

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:

Пример №42.4.

Решить уравнение: .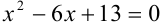

Решение:

Найдем дискриминант: .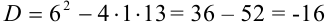

Тогда .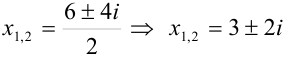

Ответ: .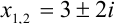

Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.

Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение -й степени имеет комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Другие лекции по высшей математике, возможно вам пригодятся:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института