Корни уравнения это точки пересечения

Графический способ решения уравнений в среде Microsoft Excel 2007

Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.

Цели и задачи урока:

• повторение изученных графиков функций;
• повторение и закрепление графического способа решения уравнений;
• закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
• формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
• формирование мышления, направленного на выбор оптимального решения;
• формирование информационной культуры школьников.

Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.

Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).

Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).

Объявление темы урока.

1. Устная работа (актуализация знаний).

Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):

у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; .

Слайд 3 Графический способ решения уравнений вида f(x)=0.

Корнями уравнения f(x)=0 являются значения х₁, х₂, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).

Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).

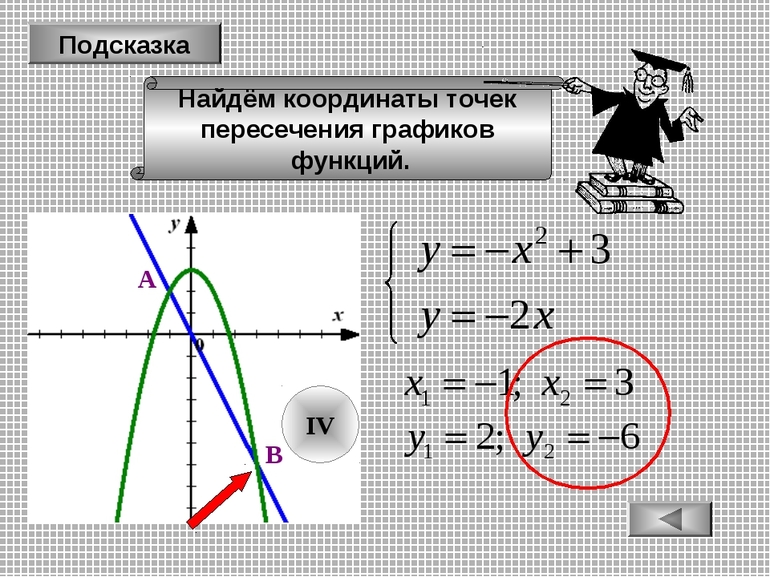
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).

Корнями уравнения f(x)=g(x) являются значения х₁, х₂, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):

Слайд 6 Найдите корни уравнения , используя графический способ решения уравнений (Рис. 5).

2. Объяснение нового материала. Практическая работа.

Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).

I. Графический способ решения уравнений вида f(x)=0 в Excel.

Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.

Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.

Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; \найти значения х точек пересечения графика функции с осью абсцисс.

Выполнение задания можно разбить на этапы:

1 этап: Представление функции в табличной форме (рис. 6):

• в ячейку А1 ввести текст Х, в ячейку A2 — Y;
• в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
• выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).

При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.

После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):

• скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.

2 этап: Построение диаграммы типа График.

• выделить диапазон ячеек B2:V2;
• на вкладке Вставка|Диаграммы|График выбрать вид График;
• на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;

• на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:

Интервал между делениями: 4;

Интервал между подписями: Единица измерения интервала: 4;

Положение оси: по делениям;

Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);

• самостоятельно изменить ширину и цвет линии для вертикальной оси;
• на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.

Примерный результат работы приведен на рис. 10:

3 этап: Определение корней уравнения.

График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х₁=1; х₂=4.

II. Графический способ решения уравнений вида f(x)=g(x) в Excel.

Пример 2: Решить графическим способом уравнение .

Для этого: в одной системе координат построить графики функций у₁= и у₂=1-х на промежутке [ -1; 4 ] с шагом 0,25; найти значение х точки пересечения графиков функций.

1 этап: Представление функций в табличной форме (рис. 1):

Аналогично Примеру 1, применив приемы копирования, заполнить таблицу. При табулировании функции у₁=воспользоваться встроенной функцией Корень (Рис. 11).

2 этап: Построение диаграммы типа График.

Примерный результат работы приведен на Рис. 12:

3 этап: Определение корней уравнения.

Графики функций у₁= и у₂=1-х пересекаются в одной точке (0;1) и, следовательно, уравнение имеет один корень – абсцисса этой точки: х=0.

III. Метод Подбор параметра.

Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.

Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.

Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.

1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.

Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.

• выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
• с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.

Все изменения сразу отобразятся на графике.

Примерный результат работы приведен на Рис. 13:

2 этап: Определение приближенных значений корней уравнения.

График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.

По графику приближенно можно определить, что х₁≈0,7; х₂≈4,3.

3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.

1) Начать с поиска более точного значения меньшего корня.

По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.

• Выделить ячейку Е2;
• перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;

В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.

В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).

Щелкнуть по кнопке ОК.

• В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
• В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).

Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).

Итак, первый корень уравнения определен с заданной точностью: х₁≈0,6972.

2) Самостоятельно найти значение большего корня с той же точностью. (х₂≈4,3029).

IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).

При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.

3. Закрепление изученного материала. Самостоятельная работа.

Задание: Используя метода Подбор параметров, найти корни уравнения с точностью до 0,001.

• ввести функцию у=и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):

• найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
• найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).

4. Итог урока.

Слайд 12 Проверка результатов самостоятельной работы.

Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.

Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).

5. Домашнее задание.

Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.

Решение квадратных уравнений

Квадратное уравнение – это математическое уравнение, которое в общем виде выглядит так:

Это многочлен второго порядка с 3 коэффициентами:

• a – старший (первый) коэф., не должен быть равен 0;
• b – средний (второй) коэф.;
• c – свободный элемент.

Решением квадратного уравнения является нахождение двух чисел (его корней) – x₁ и x₂.

Формула для вычисления корней

Для нахождения корней квадратного уравнения используется формула:

Выражение внутри квадратного корня называется дискриминантом и обозначается буквой D (или Δ):

Таким образом, формула для вычисления корней может быть представлена разными способами:

1. Если D > 0, у уравнения есть 2 корня:

2. Если D = 0, уравнение имеет всего один корень:

3. Если D Решений квадратных уравнений

Пример 1

Решение:

Пример 2

Решение:

Пример 3

Решение:

В данном случае нет вещественных корней, а решением являются комплексные числа:

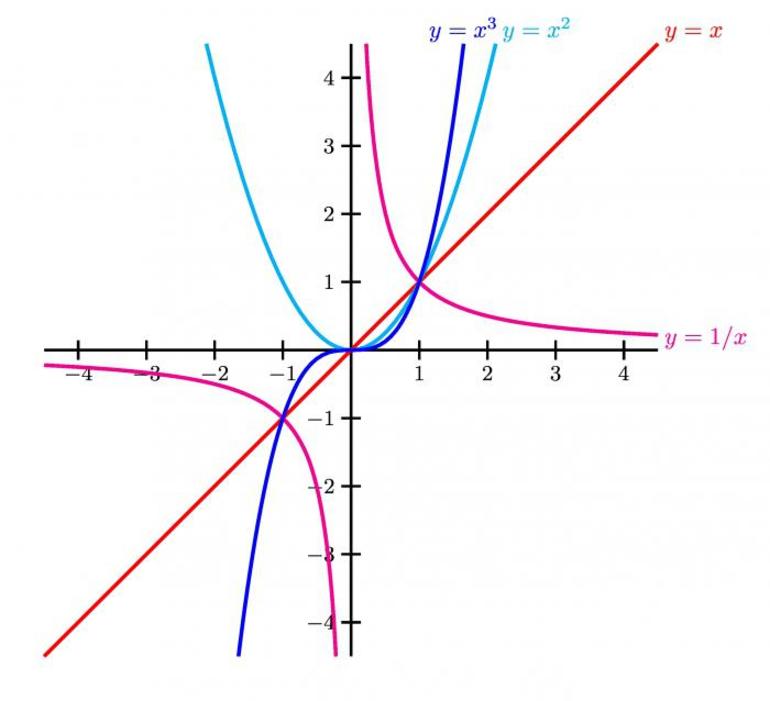
График квадратичной функции

Графиком квадратичной функции является парабола.

• Корни квадратного уравнения – это точки пересечения параболы с осью абцисс (X).
• Если корень один – парабола касается оси в одной точке, не пересекая ее.
• При отсутствии вещественных корней (наличии комплексных), график с осю X не соприкасается.

Как найти точки пересечения графиков функций — алгоритмы и примеры правила и методики

Общие сведения

Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.

Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.

Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.

Классификация уравнений

Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:

Линейными являются уравнения, содержащие единичную степень, т. е. 2t=4. Квадратные — тождества, у которых переменная возведена в квадрат. Они имеют следующий вид: Pt^2+St+U=0, где Р и S — коэффициенты при неизвестных, а U — свободный член.

Кубическое — уравнение вида Ot^3+Pt^2+St+U=0, где O, Р и S — коэффициенты при переменных, а U — константа. Последний вид — равенства, в которых при переменной присутствует четвертая степень (Nt^4+Ot^3+Pt^2+St+U=0).

Равносильные тождества

При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.

Формулировка первого: когда I уравнение равносильно II, то значит, и II равносильно I. Суть транзитивности состоит в том, что если I равносильно II, а II — III, то значит I эквивалентно III. Второе свойство имеет такую формулировку: произведение двух элементов, содержащих переменные, равное нулевому значению, эквивалентно двум выражениям, которые можно приравнять к 0. Математическая запись утверждения имеет такой вид: R(t)*S(t)=0 .

Математические преобразования

Для решения уравнения необходимо выполнить некоторые математические преобразования. Они должны выполняться грамотно, поскольку любая ошибка приводит к образованию ложных корней. Допустимыми операциями являются следующие:

1. Правильное раскрытие скобок с учетом алгебраической операции и знаков.
2. Упрощение выражения (приведение подобных величин).
3. Перенос элементов в любые части равенства с противоположным знаком.
4. Возможность прибавлять или вычитать эквивалентные величины.
5. Деление и умножение на любые эквивалентные значения, не превращающие тождества в пустое множество.

Специалисты рекомендуют избегать операций, при которых сокращаются неизвестные величины. Следствием этого могут стать ложные корни. Кроме того, делитель не должен иметь значения, при которых его значение равно 0. Последнее условие следует всегда проверять, а при решении ни один корень уравнения не должен соответствовать значению переменной при нахождении окончательных корней.

Иными словами, в выражении (t+2)^2=0 для упрощения можно разделить обе части на (t+2) при условии, что t не равно -2, т. к. [(t+2)^2]/(t+2)=0/(t+2).

Однако при решении (t+2)=0 получается, что t=-2, а это недопустимо. Следовательно, вышеописанный метод не всегда подходит.

Разложение на множители

Для решения уравнений при выполнении математических преобразований могут потребоваться специальные формулы разложения на множители. Их еще называют тождествами сокращенного умножения. К ним относятся следующие:

1. Квадрат суммы и разности: (p+r)^2=p^2+2pr+r^2 и (p-r)^2=p^2-2pr+r^2 соответственно.
2. Разность квадратов: p^2-r^2=(p-r)(p+r).

В некоторых случаях можно воспользоваться сразу двумя соотношениями, т. е. выделить квадрат суммы, а затем из первого — разность квадратов. Выделение первого осуществляется группировкой посредством скобок в выражении, а затем введение положительного и отрицательного элементов, т. е. s^2+4s-5=s^2+4s+4-4-5=(s^2+4s+4)-4-5=(s+2)^2 -9. Для получения всех элементов формулы «p+r)^2=p^2+2pr+r^2» нужно прибавить, а затем отнять 4. При этом значение равенства не изменится, поскольку 4-4=0.

Следует отметить, что математические преобразования выражения (s+2)^2 -9 не заканчиваются, поскольку его можно представить в виде разности квадратов, т. е. (s+2-9)(s+2+9)=(s-7)(s+11). Кроме того, формулы сокращенного умножения рекомендуется применять при понижении степени.

Методики нахождения точек

Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.

Первой и второй степени

Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные — в другую сторону. Методика решения имеет следующий вид:

1. Раскрыть скобки и привести подобные коэффициенты.
2. Выполнить перенос известных в одну, а неизвестных — в другую часть равенства.
3. Произвести необходимые математические преобразования.
4. Найти корень.

Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:

1. Разложить на множители.
2. Выделить полный квадрат.
3. Найти дискриминант.
4. По теореме Виета.

Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).

Однако не всегда можно быстро решить квадратное уравнение при помощи первых двух методов. Еще один вариант — нахождение корней через дискриминант (Д), т. е. дополнительный параметр, позволяющий сразу находить решения. Он находится по следующей формуле: Д=(-S)^2 -4PU.

Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д 3 +St 2 +Ut+V=0 существует еще одна методика нахождения корней. Она имеет следующий вид:

1. Уравнение требуется разделить на P.
2. Осуществить замену: t=m-(S/(3P)). При этом получается тождество вида m^3 +km+l=0.
3. Найти значение коэффициентов по формулам: k=[2S 3 -9PSU+27(P 2 )V] / (27P 3 ) и l=[(3PU-S 2 )/(3P 2 )]. Подставить их во второй пункт и найти промежуточные корни, при помощи которых найти основные значения переменных.

Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.

Пример решения

Для закрепления знаний необходимо перейти к практическому решению заданий.Одной из простых задач является следующая: найдите координаты точки пересечения графиков линейных функций z=2t+7 и z=t-1. Решается задача по такому алгоритму:

1. Приравнять уравнения: 2t+7=t-1.
2. Перенести переменные влево, а константы — вправо: 2t-t=-1-7.
3. Привести подобные коэффициенты: t=-8.
4. Найти координаты второй составляющей: z=-8-1=-9.
5. Искомая точка пересечения: (-8;-9).

В четвертом пункте нужно подставить координату по оси абсцисс в любое из уравнений для получения второй составляющей, необходимой для точки. Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.

Таким образом, для определения точки пересечения графиков необходимо уметь находить корни уравнения, а также выполнять алгебраические преобразования.