Корни уравнения в тригонометрической форме

Тригонометрическая форма комплексного числа

Рассмотрим комплексное число, заданной в обычной (алгебраической) форме:

Задача заключается в представлении комплексного числа (1) в тригонометрической форме. Для этого на комплексной плоскости введем полярные координаты. Примем за полюс начало координат, а за полярную ось вещественную ось R.

Как известно, полярными координатами точки z являются длина r ее радиус-вектора, равной расстоянию от точки z до полюса, и величина ее полярного угла, т.е. угла, образованного между полярной осью и вектором-радиусом точки z. Отметим, что направление отсчета угла берется от полярной оси до вектора-радиуса против часовой стрелки (Рис.1, Рис.2).

На Рис.3 изображено комплексное число z. Координаты этого числа в декартовой системе координат (a, b). Из определения функций sin и cos любого угла, следует:

.

.

(2)

Подставляя (2) в (1), получим:

.

(3)

Эта форма записи называется тригонометрической формой записи комплексного числа.

Уравнения (2) возведем в квадрат и сложим:

.

(4)

r−длина радиус-вектора комплексного числа z называется модулем комплексного числа и обозначается |z|. Очевидно |z|≥0, причем |z|=0 тогда и только тогда, когда z=0.

Величина полярного угла точки, соответвующей комплексному числу z, т.е. угла φ, называется аргументом этого числа и обозначается arg z. Заметим, что arg z имеет смысл лишь при z≠0. Аргумент комплексного числа 0 не имеет смысла.

Аргумент комплексного числа определен неоднозначно. Если φ аргумент комплексного числа, то φ+2πk, k=0,1. также является аргументом комплексного числа, т.к. cos(φ+2πk)=cosφ, sin(φ+2πk)=sinφ.

Приведение комплексного числа из алгебраической формы в тригонометрическую

Пусть комплексное число представлено в алгебраической форме: z=a+bi. Представим это число в тригонометрической форме. Вычисляем модуль комплексного числа: . Вычисляем аргумент φ комплексного числа из выражений или . Полученные значения вставляем в уравнение (3).

Пример 1. Представить комплексное число z=1 в тригонометрической форме.

Решение. Комплексное число z=1 можно представить так: z=1+0i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=1/1. Откуда имеем φ=0. Подставляя значения модуля и аргумента в (3), получим: z=1(cos0+isin0).

Пример 2. Представить комплексное число z=i в тригонометрической форме.

Решение. Комплексное число z=i можно представить так: z=0+1i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=0/1. Откуда имеем φ=π/2. Подставляя значения модуля и аргумента в (3), получим: .

Ответ. .

Пример 3. Представить комплексное число z=4+3i в тригонометрической форме.

Решение. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=4/5. Откуда имеем φ=arccos(4/5). Подставляя значения модуля и аргумента в (3), получим: .

Ответ. , где φ=arccos(4/5).

Умножение комплексных чисел в тригонометрической форме записи

В результате умножения комплексных чисел в тригонометрической форме мы получили комплексное число в тригонометрической форме, следовательно |z₁z₂|=r₁r₂, или

т.е. модуль произведения комплексных чисел равен произведению модулей сомножителей .

т.е. аргумент произведения комплексных чисел равен сумме аргументов сомножителей .

Пример 4. Умножить комплексные числа и .

Решение. Воспользуемся формулой (5):

Ответ. .

Деление комплексных чисел в тригонометрической форме записи

(8)

Отсюда следует, что или

(9)

Далее , или

(10)

Следовательно, модуль частного двух комплексных чисел равен модулю делимого, деленному на модуль делителя, а аргумент частного двух комплексных чисел получается вычитанием аргумента делителя от аргумента делимого .

Пример 5. Делить комплексные числа и .

Решение. Воспользуемся формулой (8):

Ответ. .

Извлечение корня из комплексного числа

Третий урок по комплексным числам. В этом уроке вы узнаете:

Начнём с ключевого определения.

1. Определение комплексного корня

Определение. Корнем $n$-й степени из комплексного числа $z$, где $n\in \mathbb$, $n \gt 1$, называется такое комплексное число $\omega $, что

т.е. $n$-я степень числа $\omega $ равна $z$.

Таких корней на множестве комплексных чисел всегда будет ровно $n$ штук. Все они обозначаются привычным знаком радикала:

Пример. Вычислить $\sqrt[3]<-1>$ на множестве комплексных чисел.

Очевидно, привычная нам единица является таким корнем, потому что $<<\left( -1 \right)>^<3>>=-1$. Но есть ещё два корня:

Итого три корня. Как и предполагалось.

Теорема. Для любого комплексного числа $z\ne 0$ существует ровно $n$ комплексных чисел, каждое из которых является корнем $n$-й степени из числа $z.$

Все эти корни считаются по следующей формуле.

2. Формула корней

Теорема. Пусть комплексное число записано в тригонометрической форме:

\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]

Тогда все корни степени $n$ из этого числа можно найти по формуле:

По сути, эта теорема является обратной к формуле Муавра:

Почему степень всегда одна, а корней несколько — об этом в конце урока. Сейчас для нас главное — алгоритм извлечения корня из комплексного числа. Он состоит из четырёх шагов:

1. Перевести комплексное число в тригонометрическую форму;
2. Записать общую формулу корня степени $n$;
3. Подставить в эту формулу $k=0$, затем $k=1$ и так до $k=n-1$.
4. Получим $n$ комплексных корней. Вместе они и будут ответом.

В ответе всегда будет набор из $n$ чисел. Потому что невозможно однозначно извлечь корень из комплексного числа $z\ne 0$.

Представим число $-8i$ в тригонометрической форме:

\[\begin -8i &=0+\left( -8 \right)\cdot i= \\ & =8\cdot \left( 0+\left( -1 \right)\cdot i \right)= \\ & =8\cdot \left( \cos \left( -\frac<\pi > <2>\right)+i\sin \left( -\frac<\pi > <2>\right) \right) \end\]

Запишем формулу корней в общем виде:

\[\sqrt[3]<-8i>=2\cdot \left( \cos \left( -\frac<\pi > <6>\right)+i\sin \left( -\frac<\pi > <6>\right) \right)=\sqrt<3>-i\]

В ответе нужно указать все три числа: $-2i$; $\sqrt<3>-i$; $-\sqrt<3>-i$.

Ещё раз: подставляя разные $k$, мы будем получать разные корни. Всего таких корней будет ровно $n$. А если взять $k$ за пределами диапазона $\left\< 0,1. n-1 \right\>$, то корни начнут повторяться, и ничего нового мы не получим.

3. Геометрическая интерпретация

Если отметить на комплексной плоскости все значения корня $n$-й степени из некоторого комплексного числа $z\ne 0$, то все они будут лежать на окружности с центром в начале координат и радиусом $R=\sqrt[n]<\left| z \right|>$. Более того: эти точки образуют правильный $n$-угольник.

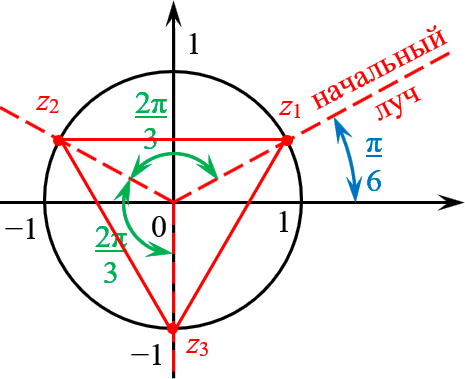
Отметить на комплексной плоскости все числа вида $\sqrt[3]$.

Представим число $z=i$ в тригонометрической форме:

\[\begin z & =1\cdot \left( 0+i\cdot 1 \right)= \\ & =1\cdot \left( \cos \frac<\pi ><2>+i\sin \frac<\pi > <2>\right) \end\]

Формула комплексных корней:

\[\sqrt[3]=1\cdot \left( \cos \left( \frac<\pi ><6>+\frac<2\pi k> <3>\right)+i\sin \left( \frac<\pi ><6>+\frac<2\pi k> <3>\right) \right)\]

Это три точки $<_<1>>$, $<_<2>>$ и $<_<3>>$ на окружности радиуса $R=1$:

Получили правильный треугольник. Его первая вершина лежит на пересечении окружности радиуса 1 и начального луча, который образован поворотом оси $OX$ на угол $<\pi >/<6>\;$.

Рассмотрим более сложный пример:

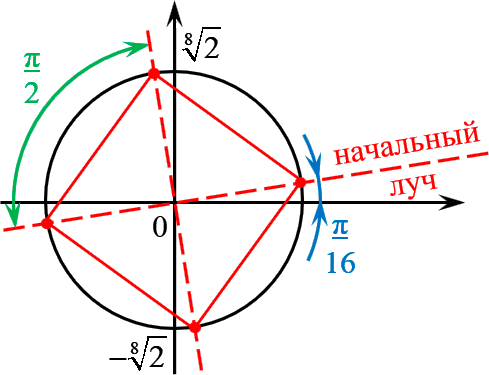
Отметить на комплексной плоскости все числа вида $\sqrt[4]<1+i>$.

Сразу запишем формулу корней с выделением начального луча:

\[\sqrt[4]=\sqrt[8]<2>\cdot \left( \cos \left( \frac<\pi ><16>+\frac<\pi k> <2>\right)+i\sin \left( \frac<\pi ><16>+\frac<\pi k> <2>\right) \right)\]

Отмечаем эти точки на комплексной плоскости. Радиус окружности $R=\sqrt[8]<2>$, начальный луч $<\pi >/<16>\;$:

И вновь всё чётко: четыре точки — правильный четырёхугольник, т.е. квадрат. С отклонением начального луча $<\pi >/<16>\;$.

Ну и ещё один пример — вновь без промежуточных вычислений. Только формулировка задачи, формула корней и окончательный чертёж:

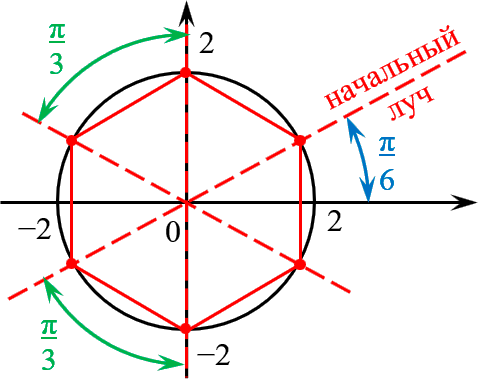
Отметить на комплексной плоскости все числа вида $\sqrt[6]<-64>$.

Формула корней с выделением начального луча:

\[\sqrt[6]=2\cdot \left( \cos \left( \frac<\pi ><6>+\frac<\pi k> <3>\right)+i\sin \left( \frac<\pi ><6>+\frac<\pi k> <3>\right) \right)\]

Получили правильный шестиугольник со стороной 2 и начальным лучом $<\pi >/<6>\;$.

Таким образом, мы получаем «графический» алгоритм извлечения корня $n$-й степени из комплексного числа $z\ne 0$:

1. Перевести число в тригонометрическую форму;
2. Найти модуль корня: $\sqrt[n]<\left| z \right|>$ — это будет радиусом окружности;
3. Построить начальный луч с отклонением $\varphi =<\arg \left( z \right)>/\;$;
4. Построить все остальные лучи с шагом $<2\pi >/\;$;
5. Получим точки пересечения лучей с окружностью — это и есть искомые корни.

Такой алгоритм прекрасно работает, когда аргумент исходного числа и отклонение начального луча $\varphi $ — стандартные «табличные» углы вроде $<\pi >/<6>\;$. На практике чаще всего именно так и бывает. Поэтому берите на вооружение.:)

4. Почему корней всегда ровно n

С геометрической точки зрения, всё очевидно: если мы будем последовательно зачёркивать вершины правильного $n$-угольника, то ровно через $n$ шагов все вершины будут зачёркнуты. И для дальнейшего зачёркивания придётся выбирать вершину среди уже зачёркнутых.

Однако рассмотрим проблему с точки зрения алгебры. Ещё раз запишем формулу корня $n$-й степени:

Последовательно подставим в эту формулу указанные значения параметра $k$:

Очевидно, последняя строка получена при $k=n-1$. Подставим теперь $k=n$:

Поскольку синус и косинус — периодические функции с периодом $2\pi $, $<<\omega >_>=<<\omega >_<0>>$, и далее корни будут повторяться. Как мы и заявляли в самом начале урока.

5. Выводы

Ключевые факты из урока.

Определение. Корень степени $n$ из комплексного числа $z$ — это такое число $\omega $, что $<<\omega >^>=z$.

Обозначение. Для обозначения комплексных корней используется знакомый знак радикала: $\omega =\sqrt[n]$.

Замечание. Если $z\ne 0$, таких чисел корней будет ровно $n$ штук.

Алгоритм нахождения корней состоит из двух шагов.

Шаг 1. Представить исходное число в тригонометрической форме:

\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]

Шаг 2. Воспользоваться формулой Муавра для вычисления корней:

Все полученные корни лежат на окружности радиуса $\sqrt[n]<\left| z \right|>$ с центром в начале координат и являются вершинами правильного $n$-угольника. Первая вершина лежит на т.н. «начальном луче», который отклонён от положительной полуоси $OX$ на угол $<\varphi >/\;$. Остальные вершины обычно легко находятся из соображений симметрии с помощью циркуля и линейки.

Геометрическую интерпретацию можно использовать для быстрого «графического» извлечения корней. Но это требует практики и хорошего понимания, что именно и зачем вы делаете. Технология такого извлечения корней описана выше в разделе «Геометрическая интерпретация».

Всё. В следующем уроке начнём решать уравнения в комплексных числах.:)

Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.

Рассматривать будем на таком примере:

Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:

Выполним проверку того, что эти корни и права оказываются решением уравнения:

Что и требовалось доказать.

Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: .

Такие корни являются сопряженными комплексными корнями.

Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:

, ,

,

,

В каждом случае получаем 2 сопряженных комплексных корня.

Решим квадратное уравнение .

Первым шагом определим дискриминант уравнения:

В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:

Как известно из формул дискриминанта у нас образуется 2 корня:

– сопряженные комплексные корни

Т.о., у уравнения есть 2 сопряженных комплексных корня:

,

Теперь можно решить любое квадратное уравнение!

У любого уравнения с многочленом n-ой степени есть ровно n корней, некоторые из них могут быть комплексными.

Как извлечь корень из произвольного комплексного числа?

Рассмотрим уравнение z n = w, либо, записав в другом виде: . Здесь n может принимать всякое натуральное значение, которое больше 1-цы.

В частности, при n = 2 получаем квадратный корень .

У уравнения типа есть ровно n корней ­z₀, z₁, z₂, … z_n-1, которые можно вычислить с помощью формулы:

,

где – это модуль комплексного числа w,

φ – его аргумент,

а параметр k принимает значения: .

Найдем корни уравнения: .

Перепишем уравнение как: .

В этом примере , , поэтому у уравнения будет 2 корня: z₀ и z₁. Детализируем общую формулу:

, .

Далее найдем модуль и аргумент комплексного числа :

Число w находится в 1-ой четверти, значит:

Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.

Детализируем еще немного общую формулу:

, .

Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.

Подставляем в формулу значение k = 0 и получаем 1-й корень:

.

Подставляем в формулу значение k = 1 и получаем 2-й корень:

.

Ответ: ,

Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.

Часто вычисленные корни нужно изобразить геометрически:

Как выполнить чертеж?

Для начала на калькуляторе вычисляем, чему равен модуль корней и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.

Далее берем аргумент 1-го корня и вычисляем, чему равен угол в градусах:

.

Отмеряем транспортиром 45° и ставим на чертеже точку z₀.

Берем аргумент 2-го корня и переводим его тоже в градусы: . Отмеряем транспортиром 165° и ставим на чертеже точку z₁.

По этому же алгоритму ставим точку z₂.

Видно, что корни располагаются геометрически правильно с интервалом между радиус-векторами. Чертеж обязательно делать при помощи транспортира.