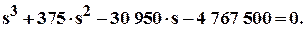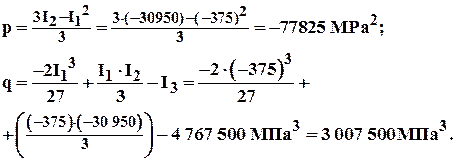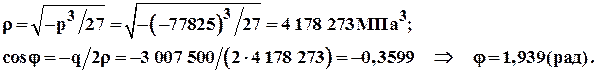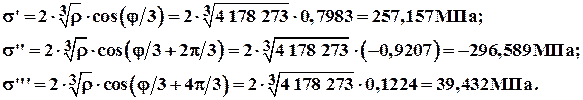Корнями какого уравнения являются значения главных напряжений
Тензор напряжений обладает свойством симметрии. Для доказательства этого свойства рассмотрим приведенный в лекции 5 элементарный параллелепипед с действующими на его площадках компонентами тензора напряжений. Так как тело находится в равновесии, следовательно, находится в равновесии любая его часть, в том числе и элементарный объем. Запишем одно из шести уравнений равновесия этого объема, а именно сумму моментов всех сил относительно оси Ох. Все силы, кроме двух, либо не создают момента относительно ocи Ох, либо взаимно уничтожаются. Отличные от нуля моменты создают компоненты 

После сокращения на элемент объема dV=dxdydz получим
Аналогично, приравнивая нулю сумму моментов всех сил относительно осей Оу и Ог, получим еще два соотношения
Эти условия симметрии и тензора напряжений называются также условиями парности касательных напряжений: касательные напряжения, действующие по двум взаимно перпендикулярным площадкам в направлениях, ортогональных ребру, образованному пересечением этих площадок, равны по величине. С учетом этих свойств из девяти компонент тензора напряжений независимыми оказываются шесть компонент.
Покажем теперь, что компоненты тензора напряжений определенные для трех взаимно перпендикулярных площадок, полностью характеризуют напряженное состояние в точке, т. е. позволяют вычислить компоненты вектора напряжений на площадках, произвольно ориентированных относительно выбранной системы координат. Для этого рассмотрим элементарный объем, образованный сечением параллелепипеда, изображенного на рис. 1, плоскостью, пересекающей координатные оси и имеющей единичный вектор нормали
Рис.1. Элементарный четырехгранник с компонентами напряженного состояния.
п с компонентами nx, ny, nz. На гранях полученного таким образом бесконечно малого тетраэдра действуют напряжения, показанные на рис. 1. При этом вектор напряжений pn на наклонной площадке разложен па составляющие рx, рy, рz вдоль координатных осей. Площади граней, ортогональных координатным осям и вектору нормали, обозначим соответственно dFx, dFy, dFz, dF. Эти площади связаны между собой соотношениями
вытекающими из того, что грани, ортогональные координатным осям, есть проекции наклонной площадки на соответствующую координатную плоскость.
Проектируя силы, действующие на гранях элементарного тетраэдра, на координатные оси, получим уравнения равновесия для рассматриваемого объема. Например, проекции всех поверхностных сил на ось Ох дают
С учетом соотношений (1) после сокращения на dF получим уравнение, связывающее проекцию рx вектора напряжений с соответствующими компонентами тензора напряжений. Объединяя это уравнение с двумя аналогичными уравнениями, полученными проектированием сил на оси Оy и Оz, приходим к следующим соотношениям
носящим название формул Коши. Эти формулы определяют вектор напряжений на произвольно выбранной площадке с вектором п через компоненты тензора напряжений.
Формулы (2) позволяют вычислить через компоненты тензора напряжений
Корнями какого уравнения являются значения главных напряжений
Определение главных напряжений


Главными напряжениями называются нормальные напряжения, действующие по площадкам, где отсутствуют касательные напряжения. Координатные оси, являющиеся нормалями к таким площадкам, называются главными осями тензора напряжений, а сами площадки – главными площадками.
Главные напряжения определяются из кубичного уравнения:

Подставляя численные значения инвариантов тензора напряжений из (2.1), получаем:
Кубические уравнения общего вида могут иметь комплексные корни, уравнения для определения главных напряжений и главных деформаций всегда имеют три действительных корня. Решать их можно по-разному.
1. Можно сначала определить подбором один из корней уравнения, а затем разложить левую часть уравнения (2.2) на два сомножителя: линейный двучлен и квадратный трехчлен. После этого из решения квадратного уравнения определяются два оставшиеся корня.
2. Существует и аналитический способ решения, для этого используются формулы Кардано.
Воспользуемся вторым способом.
Пусть задано кубическое уравнения:


получим кубичное уравнение (приведенное):

Здесь 


Формулы Кардано для случая уравнения с тремя действительными корнями имеют вид:


Далее с помощью подстановки (2.4) в (2.3) находим корни исходного уравнения.

Подстановка (2.4) с новыми обозначениями получает вид:

Здесь изменен знак второго слагаемого подстановки потому, что 
Подставляя (2.10) в (2.9) получим уравнение аналогичное (2.5):

Здесь коэффициенты 

Далее по формулам (2.7) находим:
По формулам (2.8) находим корни уравнения (2.5):
Учитывая (2.10), находим корни исходного уравнения (2.9), являющимися главными напряжениями:

В соответствии с правилом индексации главных напряжений введены обозначения: 

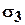
Величины 


Тензор напряжений в главных осях имеет вид:

Определение главных напряжений


Главными напряжениями называются нормальные напряжения, действующие по площадкам, где отсутствуют касательные напряжения. Координатные оси, являющиеся нормалями к таким площадкам, называются главными осями тензора напряжений, а сами площадки – главными площадками.
Главные напряжения определяются из кубичного уравнения:
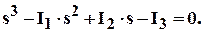
Подставляя численные значения инвариантов тензора напряжений из (2.1), получаем:
Кубичное уравнение всегда имеет три корня. При этом встретиться два случая:
1) уравнение имеет один действительный корень и два комплексно сопряженных;
2) уравнение имеет три действительных корня.
Уравнения для определения главных напряжений и главных деформаций всегда имеют три действительных корня. Решать их можно по-разному.
1. Можно сначала определить подбором один из корней уравнения, а затем разложить левую часть уравнения (2.2) на два сомножителя: линейный двучлен и квадратный трехчлен. После этого из решения квадратного уравнения определяются два оставшиеся корня.
2. Существует и аналитический способ решения, для этого используются формулы Кардано.
Воспользуемся вторым способом.
à Решение кубичного уравнения по формулам Кардано
Пусть задано кубическое уравнения:
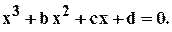
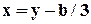
получают приведенное кубичное уравнение:
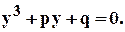
Здесь 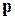
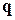
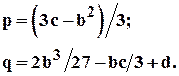
Формулы Кардано для случая уравнения с тремя действительными корнями имеют вид:
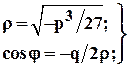
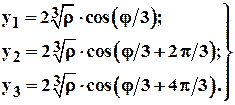
Далее с помощью подстановки (2.4) в (2.3) находят корни исходного уравнения.
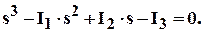
Подстановка (2.4) с новыми обозначениями получает вид:
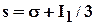
Здесь изменен знак второго слагаемого подстановки потому, что 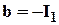
Подставляя (2.10) в (2.9) получим уравнение аналогичное (2.5):
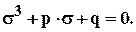
Здесь коэффициенты 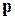
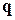
Далее по формулам (2.7) находим:
По формулам (2.8) находим корни уравнения (2.11):
Учитывая (2.10), находим корни исходного уравнения (2.9), являющимися главными напряжениями:
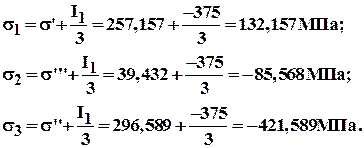
В соответствии с правилом индексации главных напряжений введены обозначения: 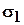
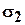
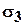
Величины 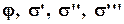
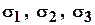
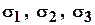
Тензор напряжений в главных осях имеет вид:
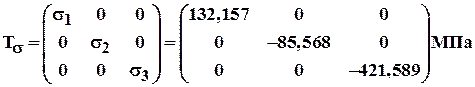
Корнями какого уравнения являются значения главных напряжений
В каждой точке твердого деформируемого тела всегда существуют такие три взаимно ортогональные площадки, на которых касательные напряжения равны нулю. Они называются главными. Направления нормалей к главным площадкам образуют главные оси тензора напряжений, не зависящие от исходной системы координат. Напряжения, действующие на главных площадках, называются главными. Главные оси нумеруем так, чтобы выполнялись неравенства
Главные напряжения являются действительными корнями кубического уравнения [196]:
Коэффициенты этого уравнения,
не зависят от выбора системы координат и называются первым (линейным), вторым (квадратичным) и третьим (кубическим) инвариантами тензора напряжения. Выражения для инвариантов в главных напряжениях имеют вид
Инварианты тензора напряжений (1.16) и (1.17) являются основными характеристиками напряженного состояния в точке твердого деформируемого тела.
Аналогично записываются выражения для инвариантов шарового тензора и девиатора напряжения:
С учетом зависимостей (1.8) выражение (1,19) преобразуется к виду
Инварианты девиатора напряжения можно выразить через главные компоненты девиатора напряжений:
где 
Определение главных напряжений и главных площадок
Если по граням выделенного элементарного параллелепипеда действуют одни только нормальные напряжения, то они называются главными напряжениями , а площадки, на которых они действуют, называются главными площадками . Можно доказать, что в каждой точке напряженного тела существуют три главные взаимно перпендикулярные площадки (рис.3.6.). Главные напряжения обозначают s 1 , s 2 , s 3 . При этом большее (с учетом знака) главное напряжение обозначается s 1 , а меньшее (с учетом знака) обозначается s 3 . Различные виды напряженного состояния классифицируются в зависимости от числа возникающих главных напряжений. Если отличны от нуля все три главных напряжения, то напряженное состояние называется трехосным или объемным (рис. 3.6). Если равно нулю одно из главных напряжений, то напряженное состояние называется двухосным или плоским . Если равны нулю два главных напряжения, то напряженное состояние называется одноосным или линейным .
Рис. 3.6. Главные напряжения
Для определения главных напряжений предположим, что площадка abc (рис. 3.5) является главной площадкой. Тогда на ней будут действовать только нормальные напряжения, то есть главные напряжения будут равны полным напряжениям p . В этом случае компоненты вектора полного напряжения p 1 , p 2 , p 3 можно рассматривать как проекции главных напряжений на оси координат:

Подставив это условие в уравнение (3.9), получим

Эти уравнения можно рассматривать как систему линейных однородных уравнений относительно направляющих косинусов. В силу известного соотношения:
направляющие косинусы не могут одновременно иметь нулевые значения. В этом случае определитель, составленный из коэффициентов системы (3.16) должен быть равен нулю:
Раскрыв определитель, получим характеристическое уравнение третьего порядка:


называются инвариантами напряженного состояния в точке, так как они не изменяют своей величины при изменении направления исходной системы прямоугольных координат. Можно доказать существование трех действительных корней уравнения (3.19). На основании этого можно считать, что в каждой точке тела, независимо от его формы и размеров, места приложения, вида и характера нагрузок, существует не более трех взаимно ортогональных главных напряжения.
Для определения положения главных площадок необходимо знать направляющие косинусы нормали к этой площадке. Для их определения следует воспользоваться системой уравнений (3.16). Однако равенство нулю определителя этой системы указывает на то, что не все уравнения системы являются линейно независимыми; одно из них есть следствие двух других. Чтобы сделать систему определенной, надо добавить к ней равенство (3.17). После этого число независимых уравнений становится достаточным для однозначного определения направляющих косинусов.
http://plastep.ru/kornyami-kakogo-uravneniya-yavlyayutsya-znacheniya-glavnyh-napryazheniy/
http://mysopromat.ru/uchebnye_kursy/sopromat/napryazheniya_deformatsii/opredelenie_glavnyh_napryazhenii_i_glavnyh_ploschadok/