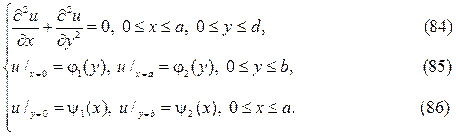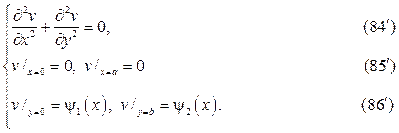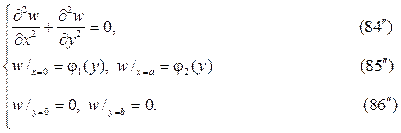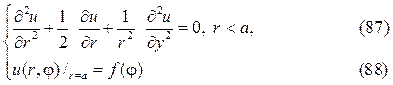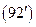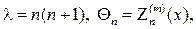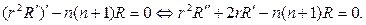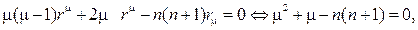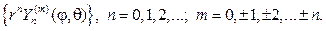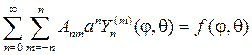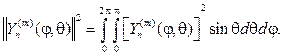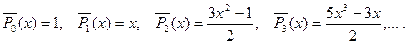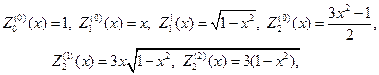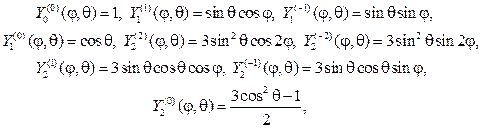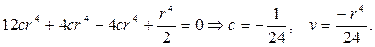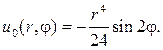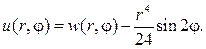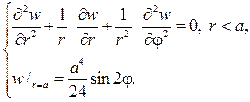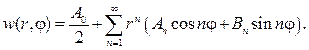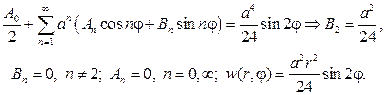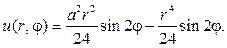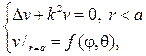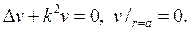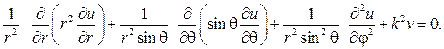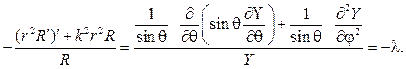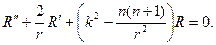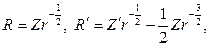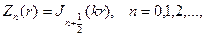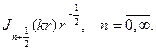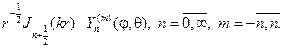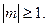Методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных» Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Ахметова Фания Харисовна, Чигирёва Ольга Юрьевна
В статье предлагается методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных » в курсе «Уравнения математической физики». Приведены краткие теоретические сведения, связанные с применением метода разделения переменных . Показана общая схема решения краевых задач для уравнения Лапласа для указанных областей. Основные этапы решения сведены в таблицы. Подробно разобраны типовые задачи домашнего задания. Содержание статьи будет полезно студентам, а также преподавателям соответствующих курсов.
Похожие темы научных работ по математике , автор научной работы — Ахметова Фания Харисовна, Чигирёва Ольга Юрьевна
Текст научной работы на тему «Методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных»»
Ахметова Ф. Х., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных» // Научно-методический электронный журнал «Концепт». -2018. — № V10. — 0,3 п. л. — URL: http://e-koncept.ru/2018/186094.htm.
ART 186094 УДК 378.147
Ахметова Фания Харисовна,
кандидат физико-математических наук, доцент ФГБОУ ВО «Московский государственный технический университет им. Н. Э. Баумана», г. Москва dobrich2@mail.ru
Чигирёва Ольга Юрьевна,
кандидат физико-математических наук, доцент ФГБОУ ВО «Московский государственный технический университет им. Н. Э. Баумана», г. Москва k fn12@bmstu.ru
Методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных»
Аннотация. В статье предлагается методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных» в курсе «Уравнения математической физики». Приведены краткие теоретические сведения, связанные с применением метода разделения переменных. Показана общая схема решения краевых задач для уравнения Лапласа для указанных областей. Основные этапы решения сведены в таблицы. Подробно разобраны типовые задачи домашнего задания. Содержание статьи будет полезно студентам, а также преподавателям соответствующих курсов.
Ключевые слова: метод разделения переменных, задача Штурма — Лиувилля, уравнение Лапласа, краевая задача. Раздел: (01) отдельные вопросы сферы образования.
Математическая физика — это наука о математических моделях физических процессов. Она является важной частью образования выпускника технического университета, поскольку носит междисциплинарный характер. Одни и те же дифференциальные уравнения в частных производных описывают процессы различной природы: физические, химические, экологические, биологические и экономические. Методы математической физики также находят применение при моделировании различных технических устройств. Поэтому при подготовке студентов ставится методическая задача преподавания данной дисциплины в такой форме, которая позволит будущим специалистам не только овладеть математическим аппаратом, но и научиться применять его при решении прикладных задач.
Особое место среди методов решения задач математической физики занимают аналитические методы: метод разделения переменных, метод функции Грина и метод интегральных преобразований [1, 2]. В данной работе рассматривается применение метода разделения переменных при решении краевых задач для уравнения Лапласа для круга и кольца. Используя многолетний опыт преподавания данной дисциплины, авторы систематизировали необходимый теоретический материал [3, 4] и представили общую схему решения краевых задач для указанных областей в наиболее компактной форме. Рассмотренные в работе примеры решения краевых задач содержат подробные пояснения. Такой структурированный подход к изложению материала поможет студентам при самостоятельном изучении данной темы.
научно-методический электронный журнал
issn 2304-120Х Ахметова Ф. Х., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных» // Научно-методический электронный журнал «Концепт». -2018. — № V10. — 0,3 п. л. — URL: http://e-koncept.ru/2018/186094.htm.
научно-методический электронный журнал
Для описания стационарных процессов в физике обычно используют уравнения эллиптического типа. Наиболее распространенным уравнением этого типа является уравнение Лапласа:
где А — дифференциальный оператор 2-го порядка, называемый оператором Лапласа.
К уравнению Лапласа приводят задачи о стационарном тепловом состоянии однородного тела, равновесном распределении электрических зарядов на поверхности проводника, об установившемся движении несжимаемой жидкости и многие другие [5].
Постановка краевых задач для уравнения Лапласа
Краевая задача для уравнения Лапласа состоит в нахождении функции и (М),
удовлетворяющей в области О уравнению Лапласа и некоторому условию, заданному на границе Е этой области. Такое условие называют граничным и в зависимости от его вида рассматривают следующие краевые задачи:
— первую краевую задачу, или задачу Дирихле, если задано граничное условие 1 -го рода
вторую краевую задачу, или задачу Неймана, если задано граничное условие 2-го рода
третью краевую задачу, если задано граничное условие 3-го рода
где у (Р), I = 1,3 и к (Р )> 0 (к (Р 0) — функции, заданные на границе Е области О;
Я — внешняя нормаль к границе Е.
Если область, в которой поставлена краевая задача, ограничена, то такая задача называется внутренней.
Если область, в которой поставлена краевая задача, является частью пространства, лежащей вне некоторой ограниченной области, то краевая задача называется внешней [6, 7].
При постановке внешней краевой задачи помимо граничного условия необходимо задать условие, описывающее поведение искомой функции на бесконечности. Для задач на плоскости таким условием является ограниченность искомой функции на бесконечности.
Основные свойства 1-й и 2-й внутренних и внешних краевых задач на плоскости
1. Решение внутренней (внешней) задачи Дирихле на плоскости единственно.
2. Внутренняя (внешняя) задача Дирихле на плоскости разрешима при любой непрерывной функции у (Р).
3. Решение внутренней (внешней) задачи Неймана на плоскости определяется с точностью до произвольной аддитивной постоянной.
issn 2304-120X Ахметова Ф. Х., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных» // Научно-методический электронный журнал «Концепт». -2018. — № V10. — 0,3 п. л. — URL: http://e-koncept.ru/2018/186094.htm.
научно-методический электронный журнал
4. Внутренняя (внешняя) задача Неймана на плоскости разрешима при любой непрерывной функции / (Р), удовлетворяющей условию
где Ь — граница области О (замкнутый контур).
Общая схема решения краевых задач для уравнения Лапласа для круга методом разделения переменных
Введем полярную систему координат (г,ф) с полюсом, совпадающим с центром
круга радиусом Я.
Учитывая, что оператор Лапласа в полярных координатах имеет вид
запишем 3-ю краевую задачу для круга (см. табл. 1).
Постановка 3-й краевой задачи для уравнения Лапласа
Внутренняя краевая задача Внешняя краевая задача
Для значения 0 получаем дифференциальное уравнение
d f dX, ^ r— r—- 1 = 0, dr^ dr )
интегрируя которое находим
X0 (r ) = A + B0 !n r ,
где A и B — произвольные постоянные.
Так как функция lnr при r ^ 0 и r ^ да не ограничена, то для внутренней и внешней краевых задач константу B0 следует положить равной нулю. Таким образом, X0 (r) = A.
При Хп= п2, п е N приходим к следующему дифференциальному уравнению:
r2X„'(r) + rX’n (r)-и2Xn (r) = 0 . Частными решениями этого уравнения являются две линейно независимые функции: X^(r) = rn (ограничена при r ^ 0 и не ограничена на бесконечности) и
Xf)(r) = -1 (ограничена на бесконечности и не ограничена при r ^ 0).
В результате получены решения уравнения (1) в следующем виде:
— для внутренней краевой задачи:
U0 (r,р) = X0 (r )Ф0 (р) = A ,
un (r, р) = Xn (r) Фn (р) = rn (An cos пр + Bn sin пр), и е N;
— для внешней краевой задачи:
U0 (r,р) = X0 (r )Ф0 (р) = A0 ,
un (r,v) = Xn (r) 1Фп (
issn 2304-120X Ахметова Ф. Х., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных» // Научно-методический электронный журнал «Концепт». -2018. — № V10. — 0,3 п. л. — URL: http://e-koncept.ru/2018/186094.htm.
научно-методический электронный журнал
В силу линейности и однородности уравнения (1) сумма всех таких решений
также будет удовлетворять этому уравнению.
В табл. 2 приведена форма записи решения (9) для различных типов краевых задач.
Вид решения краевой задачи для уравнения Лапласа для круга
Тип краевой задачи Форма записи решения краевой задачи (1), (2)
Внутренняя краевая задача u (r,p) = A + ¿ f Г j (An cos np + Bn sin np) (10)
Внешняя краевая задача x frY u (r,p) = A) +Xf R \ (An cos np + Bn sin np) (11)
Замечание. Для 1 -й и 2-й краевых задач форма записи решений имеет тот же вид, что и для 3-й краевой задачи.
Определим коэффициенты A, A и Bn таким образом, чтобы решение, записанное в виде ряда (10) для внутренней краевой задачи и в виде ряда (11) для внешней краевой задачи, удовлетворяло граничному условию (2).
В результате подстановки (10) и (11) в граничное условие (2) приходим к следующим равенствам:
для внутренней краевой задачи:
Х-г (An cos np + Bn sin np) + h A cos —p + Bn sin np 1 = f (p);
— для внешней краевой задачи:
¡; l(An cosnp + Bn sinnp) + h A0 + ^ An cosnp + Bn sinnp 1 = f (p).
n=1 V R J V n=1 J
Таким образом, для внутренней и внешней краевых задач получаем соотношение
A0h + ¿ (h + n^ (An cos nP + Bn sin nP) = f (p) —
которое представляет собой разложение функции f (p) в ряд Фурье по системе собственных функций <1,cosnp,sinnpf задачи Штурма - Лиувилля. Коэффициенты
Фурье C0 = Ah , C = h + —J A и Dn = h + —| Bn этого разложения вычисляются по формулам
Co =— j f (р)dP. Cn = — j f (p)cosnp¿/p;
Dn = » j f (P) SÍn nPdP ■
issn 2304-i20x Ахметова Ф. Х., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных» // Научно-методический электронный журнал «Концепт». -2018. — № V10. — 0,3 п. л. — URL: http://e-koncept.ru/2018/186094.htm.
научно-методический электронный журнал
Примеры решения краевых задач для уравнения Лапласа для круга Пример 1 (внутренняя задача Дирихле). Найти решение следующей краевой задачи:
r2 dp2 U0 (2 sin2 p + sin 3p).
= 0, 0 Я, 0 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
После подстановки этого ряда в граничное условие получаем:
A + ^ A cos np + B sin np = U0 (sin p + cos 2p),
откуда находим значения коэффициентов Фурье:
A = 0; A = U0; An = 0, n e N \ <2>;
B = Uo; Bn = 0, n e N \ <1>.
В результате решение краевой задачи (13) примет вид:
Пример 3 (внутренняя задача Неймана). Найти значение параметра а , при котором разрешима внутренняя задача Неймана, и решить эту задачу:
issn 2304-120X Ахметова Ф. Х., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных» // Научно-методический электронный журнал «Концепт». -2018. — № V10. — 0,3 п. л. — URL: http://e-koncept.ru/2018/186094.htm.
научно-методический электронный журнал
= 0, 0 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
n 1 n Dn V R1 У
CnRT1-D» —»»71- sin np = f2 (p). (18)
Для каждой функции fk (р), к = 1,2 запишем разложение в ряд Фурье на отрезке [0,2^] по системе функций <1,cosnp,sinnp>^ :
fk (р) = «0к) + J ■) cos nP + РП) sin nP- (19)
где а(к), af) и рк) — коэффициенты Фурье этих функций, вычисляемые по формулам:
«о) = ^ f f (p) dP — «) = — f fk (p) cos «PdP;
߻k)=- f fk (p)sin npdp. n i
Замечая, что соотношения (17) и (18) представляют собой разложения функций / (р) и / (р) соответственно в ряды Фурье по системе собственных функций
<1,^ ир^т ир>^ задачи Штурма — Лиувилля, приравняем коэффициенты Фурье в разложениях (17) и (19) для функции / (р), а также в разложениях (18) и (19) для функции / (р). В результате получим системы уравнений относительно неизвестных коэффициентов А0, В0, А, Вп, Сп и Вп:
МЕТОД РАЗДЕЛЕНИЯ ДЛЯ УРАВНЕНИЙ
ЭЛЛИПТИЧЕСКОГО ТИПА
Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма 
следует искать в виде суммы u(x,y)=v(x,y)+w(x,y),где v(x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач
Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.
Рассмотрим задачу Дирихле для круга
где f(j)кусочно-непрерывная функция.
Следуя схеме метода Фурье полагаем
подставляем в (87) и разделяем переменные. В результате получим ра -венство
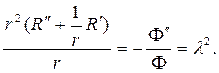
Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма 
откуда следует, что
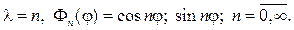
Возвращаясь к (80), решаем уравнение для радианальной функции. При
r 2 R² + rR¢ 
решение следует искать в виде степенной функции R=r m . Для определе- ния m получим соотношение
m(m 
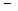
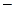
Если же n=0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции
R0(r) = 1; lnr.
С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге
Если предположить, что ряд
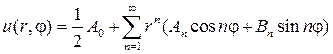
можно дифференцировать почленно дважды по r и j , то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем
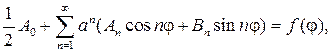
откуда с учетом формул коэффициентов Фурье следует
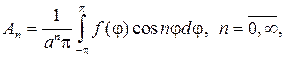
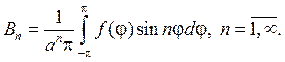

Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r — n и lnr, поскольку они разрывны в
центре круга r=0.
Напротив, если рассматривать область r>a, то нельзя привлекать r — n и lnr, и общий вид гармонической функции для внешности круга будет да- ваться рядом
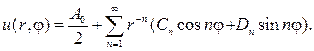
В случае кругового кольца a 2 q= 1-x 2 , найдем
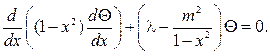
Соответственно и граничные условия (105) перейдут после замены в неравенства
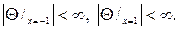
Задача (104¢) 
и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):
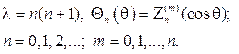
Составив произведения функций (106) на найденные выше функции Fm(j), получим множество решений уравнения (102)
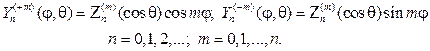
Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.
Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m1¹m2 или n1¹n2
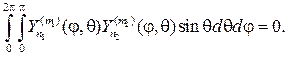
Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции
Оно имеет решение в виде степенной функции R=r m . Действительно, после подстановки
откуда находим значения m=n; 
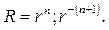
Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:
Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами
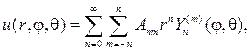
который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.
Для нахождения коэффициентов Аnm подставим (110) в (100), тогда
и с учетом (108) найдем
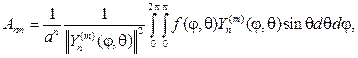
Последний интеграл вычисляется и при m=0 :
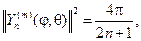
если же |m| ³ 1, то имеем

Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).
Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам
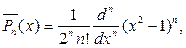
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.
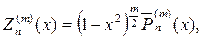
в частности будем иметь
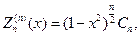
где Сn определенная константа.
С учетом (107), (115) и (116) выпишем несколько сферических функций:
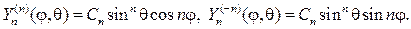
Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд
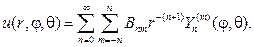
Общий вид гармонической функции в шаровом слое a 4 , и получим
Таким образом, частным решением будет функция
Вводим новую неизвестную функцию w(r,j) , полагая
Тогда относительно w(r,j) нужно решать задачу Дирихле для урав- нения Лапласа
Согласно (93), решение этой задачи дается формулой
Подставляя ее в граничное условие, получим
Ответом в задаче будет функция
254. Найдите решение первой краевой задачи для уравнения Гельмгольца
предполагая, что k не является собственным значением задачи
Р е ш е н и е. Запишем уравнение в сферических координатах
Беря u(r,j,q,)=R(r)Y(j,q), после разделения переменных придем к дифференциальным уравнениям:
Функция 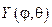
Относительно радиальной функции R(r) нужно решать дифференци- альное уравнение
Выполняя в этом уравнении замену
придем к соотношению относительно новой функции Z(r):
Последнее уравнение в качестве ограниченных в окрестности нуля
r=0 решений имеет бесселевы функции
соответственно будем иметь набор радиальных функций
Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:
Составляем ряд с числовыми коэффициентами
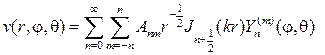
и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a
где d = 4 при m = 0 и d =2 при
При найденных коэффициентах Anm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.
255. Найдите такую гармоническую u(r,j,q) функцию внутри шарового слоя 1
http://lektsii.org/8-63359.html