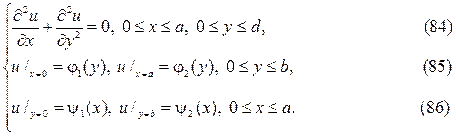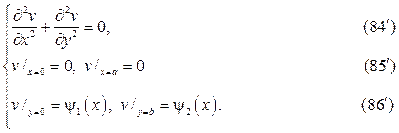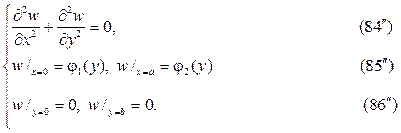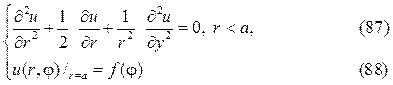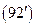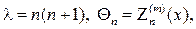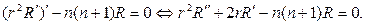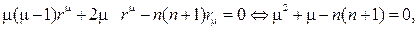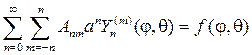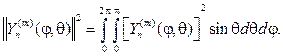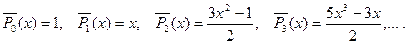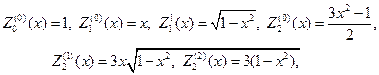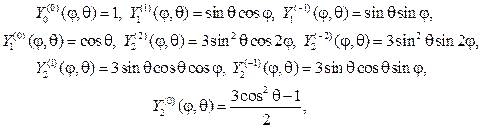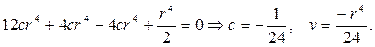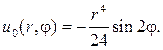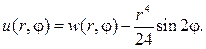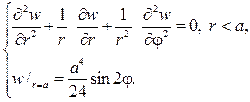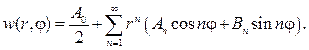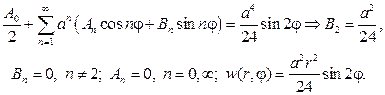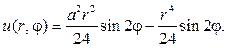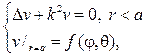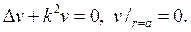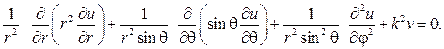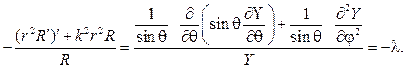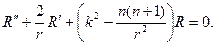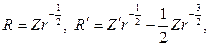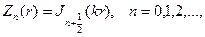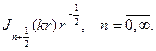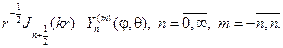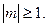Краевая задача для уравнения лапласа в треугольнике

МЕТОД РАЗДЕЛЕНИЯ ДЛЯ УРАВНЕНИЙ

ЭЛЛИПТИЧЕСКОГО ТИПА

Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма Лиувилля своеобразны, их граничные ус- ловия определяются спецификой областей:

следует искать в виде суммы u(x,y)=v(x,y)+w(x,y),где v(x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач

Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.

Рассмотрим задачу Дирихле для круга

где f(j)кусочно-непрерывная функция.

Следуя схеме метода Фурье полагаем

подставляем в (87) и разделяем переменные. В результате получим ра -венство

(90)

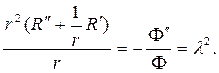
Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма Лиувилля

откуда следует, что

(91)

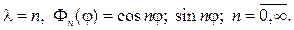
Возвращаясь к (80), решаем уравнение для радианальной функции. При

r 2 R² + rR¢ n 2 R = 0,

решение следует искать в виде степенной функции R=r m . Для определе- ния m получим соотношение

m(m 1)r m +m r m n 2 r m =0Û m 2 n 2 =0,

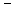
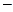
Если же n=0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции

R₀(r) = 1; lnr.

С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге

Если предположить, что ряд

(93)

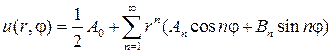
можно дифференцировать почленно дважды по r и j , то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем

(94)

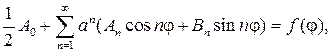
откуда с учетом формул коэффициентов Фурье следует

(95)

(96) Итог состоит в том, что решение задачи (87 88) дается рядом (93), коэффициенты которого определены равенствами (95-96).

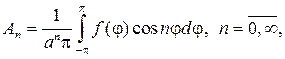
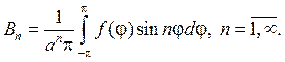
Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r — n и lnr, поскольку они разрывны в

центре круга r=0.

Напротив, если рассматривать область r>a, то нельзя привлекать r — n и lnr, и общий вид гармонической функции для внешности круга будет да- ваться рядом

(97)

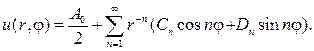
В случае кругового кольца a 2 q= 1-x 2 , найдем

(104¢)

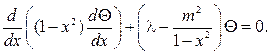
Соответственно и граничные условия (105) перейдут после замены в неравенства

(105′)

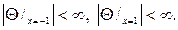
Задача (104¢) (105¢) есть известная задача для присоединенных функций Лежандра, ее решение (см., например, [3], стр. 115)

и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):

(106)

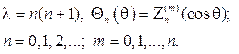
Составив произведения функций (106) на найденные выше функции F_m(j), получим множество решений уравнения (102)

(107)

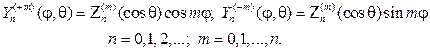
Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.

Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m₁¹m₂ или n₁¹n₂

(108)

Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции

Оно имеет решение в виде степенной функции R=r m . Действительно, после подстановки

откуда находим значения m=n; (n+1) и соответственно решения

(109)

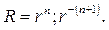
Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:

Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами

(110)

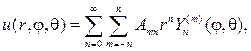
который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.

Для нахождения коэффициентов А_nm подставим (110) в (100), тогда

и с учетом (108) найдем

(111)

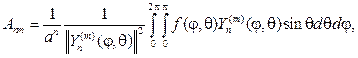
Последний интеграл вычисляется и при m=0 :

(112)

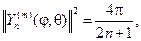
если же |m| ³ 1, то имеем

(113)

Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).

Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам

(114)

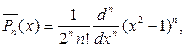
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.

(115)

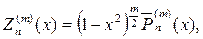
в частности будем иметь

(116)

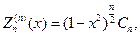
где С_n определенная константа.

С учетом (107), (115) и (116) выпишем несколько сферических функций:

(117)

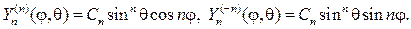
Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд

(118)

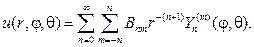
Общий вид гармонической функции в шаровом слое a 4 , и получим

Таким образом, частным решением будет функция

Вводим новую неизвестную функцию w(r,j) , полагая

Тогда относительно w(r,j) нужно решать задачу Дирихле для урав- нения Лапласа

Согласно (93), решение этой задачи дается формулой

Подставляя ее в граничное условие, получим

Ответом в задаче будет функция

254. Найдите решение первой краевой задачи для уравнения Гельмгольца

предполагая, что k не является собственным значением задачи

Р е ш е н и е. Запишем уравнение в сферических координатах

Беря u(r,j,q,)=R(r)Y(j,q), после разделения переменных придем к дифференциальным уравнениям:

Функция 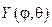будет решением уравнения (72), которое нужно решать при условии ограниченности и 2p-периодичности по j. В результате при- дем к сферическим функциям при l=n(n+1):

Относительно радиальной функции R(r) нужно решать дифференци- альное уравнение

Выполняя в этом уравнении замену

придем к соотношению относительно новой функции Z(r):

Последнее уравнение в качестве ограниченных в окрестности нуля

r=0 решений имеет бесселевы функции

соответственно будем иметь набор радиальных функций

Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:

Составляем ряд с числовыми коэффициентами

(119)

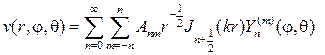
и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a

где d = 4 при m = 0 и d =2 при

При найденных коэффициентах A_nm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.

255. Найдите такую гармоническую u(r,j,q) функцию внутри шарового слоя 1

Краевые задачи для уравнения Лапласа

Автор работы: Пользователь скрыл имя, 17 Ноября 2011 в 18:30, курсовая работа

Краткое описание

Рассмотрение понятия краевой задачи для уравнений эллиптического типа. Как частный случай — уравнение Лапласа (простейшее уравнение эллиптического типа). Для уравнения Лапласа краевая задача I рода — задача Дирихле; краевая задача II рода — задача Неймана. Краевое условие III рода — смешанная краевая задача. Рассматриваются также задача Дирихле в пространств/на плоскости, решение задачи Дирихле (первой краевой задачи) для уравнения Лапласа в круге, решение задачи Неймана (второй краевой задачи) для уравнения Лапласа в круге, решение задачи Дирихле для кольца.

Содержание

Введение
Понятие краевой задачи для обыкновенного дифференциального уравнения. Краевые задачи для уравнений эллиптического типа
Уравнение Лапласа и понятие гармонической функции.
Корректность краевой задачи.
Первая и вторая краевые задачи для уравнения Лапласа.
Задача Дирихле в пространстве
Задача Дирихле на плоскости
Задача Неймана
Уравнение Лапласа в цилиндрических координатах.
Решение задачи Дирихле (первой краевой задачи) для уравнения Лапласа в круге.
Решение задачи Неймана для уравнения Лапласа в круге.
Примеры.
Решение задачи Дирихле для кольца.

Вложенные файлы: 1 файл

Понятие краевой з.doc

ПЕНЗЕНСКИЙ ПЕДАГОГИЧЕСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ В. Г. БЕЛИНСКОГО

Кафедра «Математического анализа»

«Краевые задачи для уравнения Лапласа»

1. Введение
2. Понятие краевой задачи для обыкновенного дифференциального уравнения. Краевые задачи для уравнений эллиптического типа
   1. Уравнение Лапласа и понятие гармонической функции.
   2. Корректность краевой задачи.
3. Первая и вторая краевые задачи для уравнения Лапласа.
   1. Задача Дирихле в пространстве
   2. Задача Дирихле на плоскости
   3. Задача Неймана
4. Уравнение Лапласа в цилиндрических координатах.
   1. Решение задачи Дирихле (первой краевой задачи) для уравнения Лапласа в круге.
   2. Решение задачи Неймана для уравнения Лапласа в круге.
   3. Примеры.
   4. Решение задачи Дирихле для кольца.

Уравнениями математической физики называются уравнения, описывающие математические модели физических явлений. Среди них процессы, изучаемые в теории упругости, гидродинамике, электродинамике, квантовой физике и т. д. Во многих случаях их изучение приводит к уравнениям с частными производными второго порядка.

Дифференциальным уравнением с частными производными (в частных производных) называется уравнение, связывающее функцию , независимые переменные и частные производные от функции , то есть соотношение

где известная функция и .

При этом предполагается, что в области, где рассматривается данное уравнение, функция имеет частные производные порядка

Порядок старшей из частных производных, входящих в уравнение (1), называется порядком этого уравнения. Например, уравнение второго порядка для функции, имеющей непрерывные частные производные второго порядка, в общем случае может быть записано в виде

Уравнение (1) называется линейным, если данное уравнение линейно относительно этой функции и ее производных.

Решением уравнения (1) называется всякая функция , которая, будучи подставлена в указанное уравнение, обращает его в тождество по всем переменным.

Для полного описания физических процессов помимо уравнений необходимо указать некоторые дополнительные условия. В частности, может быть задана картина процесса в фиксированный момент времени, т.е. начальные условия. Кроме того, задают значения изучаемых величин на границе рассматриваемой области – граничные (или краевые) условия. Дифференциальное уравнение вместе с соответствующими краевыми (и начальными) условиями называется краевой задачей математической физики.

К основным уравнениям математической физики относятся следующие дифференциальные уравнения в частных производных второго порядка.

Это уравнение является простейшим уравнением гиперболического типа. К его исследованию приводит изучение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводах и т.д.

1. Уравнение теплопроводности, или уравнение Фурье:

Это уравнение является простейшим уравнением параболического типа. К его исследованию приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде, изучение некоторых вопросов теории вероятностей и т.д.

Это уравнение относится к простейшим уравнениям эллиптического типа. К его исследованию приводит изучение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики и т.д.

В выписанных уравнениях искомая функция u зависит от двух переменных t, x или x, y. Рассматриваются также уравнения и для функций с большим числом переменных. Например, волновое уравнение с тремя независимыми переменными имеет вид

и уравнение Лапласа

Исключительную роль в математической физике играет уравнение Лапласа

Для уравнения Лапласа обычно считают, что необходимо найти функцию , удовлетворяющую этому уравнению внутри некоторой области , ограниченной поверхностью (кривой) , или вне этой области. Если при этом функция должна удовлетворять краевому условию

то говорят, что необходимо решить соответственно внутреннюю или внешнюю задачу Дирихле.

Если краевые условия имеют вид

где есть производная по внешней нормали к границе области , то говорят, что требуется решить задачу Неймана (внутреннюю или внешнюю).

Если краевые условия записываются в форме

то это – третья краевая задача для уравнения Лапласа.

Здесь M текущая точка границы ; , заданные функции.

Если какая-то из последних трех функций тождественно равна нулю, то соответствующее условие называется однородным.

Для уравнения теплопроводности и волнового уравнения во многих случаях приходится решать так называемую смешанную задачу, то есть задачу с начальными и граничными условиями. Если при этом на границе пространственной (плоской) области задано значение искомой функции, то говорят, что поставлена первая смешанная задача.

Если в качестве краевого условия задано значение производной от искомой функции в направлении внешней нормали к границе, то говорят, что решается вторая смешанная задача. Если задана линейная зависимость между значениями функции на границе и ее производной по нормали, то это – третья смешанная задача.

Описание многих физических явлений требует использования интегральных уравнений. Они появляются также при изучении свойств уравнений с частными производными.

Понятие краевой задачи для обыкновенного дифференциального уравнения. Краевые задачи для уравнений эллиптического типа.

Чтобы полностью описать тот или иной физический процесс, необходимо, кроме самого уравнения, описывающего этот процесс, задать начальное состояние этого процесса (начальные условия) и режим на границе той области, в которой происходит этот процесс (граничные условия). Математически это связано с не единственностью решения

дифференциальных уравнений. Действительно, даже для обыкновенных д. у. n-го порядка общее решение зависит от n-произвольных постоянных. Для уравнений же в частных производных решение, вообще говоря, зависит от произвольных функций; например, общее решение уравнения в классе функций, зависящих от переменных и , имеет вид , где — произвольная функция класса . Поэтому, чтобы выделить решение, описывающее реальный физический процесс, необходимо задавать дополнительные условия. Такими дополнительными условиями и являются краевые условия. Соответствующая задача называется краевой задачей.

Краевые условия (граничные условия)— условия, которым должно удовлетворять искомое решение заданного дифференциального уравнения на границе (или ее части) области, где это решение ищется.

Краевые условия обычно задаются с помощью дифференциальных операторов, однако встречаются краевые условия и других типов.

Различают, таким образом, следующие три основных типа краевых задач для дифференциальных уравнений:

1. Задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область совпадает со всем пространством , граничные условия отсутствуют.
2. Краевая задача для уравнений эллиптического типа: задаются граничные условия на границе , начальные условия, естественно, отсутствуют.
3. Смешанная задача для уравнений гиперболического и параболического типов: задаются и начальные и граничные условия, .

— область, где происходит процесс, — ее граница, которую считаем кусочно-гладкой поверхностью. Таким образом, есть область изменения аргументов в уравнении, описывающем стационарный процесс – область задания уравнения.

Уравнения эллиптического типа возникают обычно при исследовании стационарных процессов. Время t в эти уравнения не входит, и обе независимые переменные являются

координатами точки. Для задач такого типа ставятся только краевые условия, т. е.

указывается поведение неизвестной функции на контуре области. Для эллиптического уравнения характерно то, что краевые условия задаются на всей границе. Простейшим уравнением эллиптического типа является уравнение Лапласа.

Уравнение Лапласа является основным представителем дифференциальных уравнений с частными производными 2-го порядка эллиптического типа, на котором вырабатывались и вырабатываются основные методы решения краевых задач для эллиптических уравнений.

– уравнение Лапласа для случая функций двух независимых переменных.

–уравнение Лапласа с тремя независимыми переменными, называют оператор Лапласа или лапласиан.

Уравнение Лапласа играет важную роль в приложениях.

Например, ему должно удовлетворять всякое стационарное распределение температуры в теле.

Действительно, если температура не зависит от времени t, то и

уравнение теплопроводности , где — коэффициент

теплопроводности, сводится к уравнению Лапласа.

Применение уравнения Лапласа выходит далеко за рамки вопроса стационарного распределения температуры. Однако при изучении этого уравнения представление функции как температуры очень удобно и наглядно.