Краевые условий для параболическое уравнение

Постановка задачи для уравнения параболического типа

Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). Как отмечалось выше, в одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид:

, 0 0 (15)

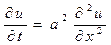
Уравнение (15), например, может описывать распространение тепла в тонком стержне длиной l, теплоизолированном по боковой поверхности. При этом функция u(x, t) задаёт значение температуры в любой точке стержня в произвольный момент времени t, при условии, что известно распределение температуры в стержне в начальный момент времени t = 0 и известна температура на концах стержня x = 0 и x = l в любой момент времени t. Таким образом, постановка задач для уравнения теплопроводности имеет следующий вид.

Первая начально-краевая задача. Если на границах стержня x = 0 и x = l заданы краевые условия первого рода, т.е. для любых моментов времени на концах стержня x = 0 и x = l заданы значения искомой функции u(x,t) (т.е. температуры):

и, кроме того, для функции u(x, t) заданы начальные условия, т.е. задано распределение температуры в любой точке стержня в момент времени t = 0:

то задачу (15) – (17) называют первой начально-краевой задачей для уравнения теплопроводности.

В терминах теории теплообмена функция u(x,t) описывает распределение температуры в пространственно-временной области W´T = <0 £ x £ l, 0 £ t £ T>, параметр а 2 – является коэффициентом температуропроводности, а краевые условия (16), (17) с помощью функций j ₁(t) и j ₂(t) задают температуру на границах
x = 0, x = l для различных моментов времени.

Вторая начально-краевая задача. Если на границах x = 0 и x = l заданы краевые условия второго рода, т.е. для x = 0 и x = l заданы значения производных искомой функции по пространственной переменной:

= j ₁(t), x = 0, t >0, (19)

= j ₂(t), x = l, t >0, (20)

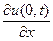
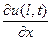
и, кроме того, для функции u(x, t) заданы начальные условия (21), то задачу (15), (19) – (21) называют второй начально-краевой задачей для уравнения теплопроводности. В терминах теории теплообмена граничные условия (19), (20) задают тепловые потоки на концах стрежня для различных моментов времени.

Третья начально-краевая задача. Если на границах x = 0 и x = l заданы краевые условия третьего рода, т.е. для x = 0 и x = l заданы линейные комбинации искомой функции и её частной производной по пространственной переменной:

+ a u(0, t) = j ₁(t), x = 0, t >0, (22)

+ b u(l, t) = j ₂(t), x = l, t >0, (23)

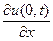
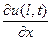
и, для функции u(x, t) заданы начальные условия (21), то задачу (15), (22), (23) называют третьей начально-краевой задачей для уравнения теплопроводности.

В терминах теории теплообмена граничные условия (22), (23) задают теплообмен между газообразной и жидкой средой (которые располагаются с разных «торцов» стержня) и границами расчётной области (т.е. внутренней частью стержня). Из-за теплообмена, температуры u(0, t) и u(l, t) на торцах стержня не известны, а известно, что температуры газообразной и жидкой среды соответственно равны
j ₁(t)/a и j ₂(t)/b. Параметры a и b являются коэффициентами теплообмена между газообразной или жидкой средой и соответствующей границей стержня.

Дата добавления: 2015-09-14 ; просмотров: 1248 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

О разрешимости краевой задачи с нелокальным граничным условием для линейных параболических уравнений Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Кожанов А. И.

Исследуется разрешимость начально-краевой задачи для линейных параболических уравнений с заданием на боковой границе условия, связывающего значения решения со значениями некоторого линейного оператора от него. Доказывается существование и единственность регулярного решения .

Текст научной работы на тему «О разрешимости краевой задачи с нелокальным граничным условием для линейных параболических уравнений»

УДК 517.9 А.И. Кожанов

О РАЗРЕШИМОСТИ КРАЕВОЙ ЗАДАЧИ С НЕЛОКАЛЬНЫМ ГРАНИЧНЫМ УСЛОВИЕМ ДЛЯ ЛИНЕЙНЫХ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ

Задача, исследуемая в настоящей работе, относится к числу нелокальных краевых задач; по своей постановке она представляет собой обобщение некоторых задач с интегральными краевыми условиями. Отметим, что задачи с интегральными условиями активно изучаются в последнее время, но при этом рассматривается в основном лишь одномерный по пространственным переменным случай — см. работы 4. В многомерном же случае можно отметить лишь работу [10], в которой рассматривалась краевая задача с граничным условием

и(Х, 0|(x,t)e3Wx(0,г) = j K(Х, У, tУ, tН ()e3Wx(0,T) (*)

(W — область изменения пространственных переменных, (0,Т) — интервал изменения временной переменной) и в которой изучались лишь свойства решений.

Перейдем к содержательной части работы.

Пусть W есть ограниченная область пространства Rn с гладкой (для простоты бесконечно- дифференцируемой) границей Г, Q есть цилиндр W х (0, Т) (0 к0 X , к0 > 0, (x, t) є Q, Х є Rn;

a(x, t) > a0 > 0, (x, t) є Q ;

— A(x, t, v) = A(x, t, vt) + Ai (x, t, v), ||A(x, t, v)|| l2(q,)

0, 1,1 = 1,_, n, (x, t) є Q, v є V1,

|^(x, t, j Vx, ^2©) 0, 1 = 1,-, n,

j e C\Q), (x, t) e Q, v e Vx; если последовательность слабо сходится в пространстве W\ (Q) к функции v(x, t), то имеет место слабая в пространстве L 2 (Q) сходимость A(x, t, jvmx ) ________® A(x, t, jvx ),

i = 1,_, n, для любой функции j(x, t) из пространства Cl(Q). (9)

Тогда для любых функций f(x, t) и u 0(x) таких, что f(x, t) e L2(Q), ft (x, t) e L2(Q), u 0(x) e W22 (W), u0(x) — A(x,0, u0) = 0 при x er, краевая задача (1)-(3) имеет решение u(x, t), принадлежащее пространству V1, и это решение единственно.

Доказательство. Введем обозначения

F(x, t, v) = Aj (x, t, v) — a11 (x, t)-A(x, t, v) + a1 (x, t)-A(x, t, v) + a(x, t) A(x, t, v) +

+ A(x, t, a11 vxx ) — A(x, t, a’vx ) — A(x, t, av), LBv = LBv + F(x, t, v).

Пусть g(x, t) есть заданная функция из пространства L 2 (Q). Рассмотрим краевую задачу: найти функцию u(x, t), являющуюся в цилиндре Q решением уравнения

и такую, что для нее выполняются условия

Bu|S = 0, Bu|(=0 = B(x, 0, u 0),. x e W. (11)

Докажем, что при выполнении условий (4)-(9) данная краевая задача имеет решение u(x, t) такое, что u(x, t) e V, Bu(x, t) e V для любой функции g(x, t), принадлежащей вместе с производной gt (x, t) пространству L 2(Q), и для любой функции u 0(x), принадлежащей пространству W2(W) и удовлетворяющей условию согласования u 0(x) — A (x,0, u0) = 0 при x e Г. Воспользуемся методом регуляризации и методом продолжения по параметру. Именно, для чисел 1 и e , l e [0,1], e > 0, определим семейство операторов : LB e ku = LBu +

+ ЯФ(x, t, u) — ea11 (x, t)(Bu)x x t.

Рассмотрим краевую задачу: найти решение уравнения

для которого выполняются условия (11).

Прежде всего покажем, что краевая задача (10еЯ), (11) имеет решение и(х, і) такое, что

и(х, і) є У2, Ви(х, і) є У2 для любого фиксированного значения числа е и для всех чисел X из

отрезка [0, 1] при принадлежности функции g(x, 0 лишь пространству Ь 2 О) . Обозначим через Л множество тех чисел X из отрезка [0, 1], для которых краевая задача (10 е л), (11) разрешима в классе функций (V : V е У2, Бу е У2 > для любых функций g(x, ^ из пространства Ь 2 О) и и 0(х), удовлетворяющей условиям теоремы. Если мы докажем, что это множество не пусто, открыто и замкнуто, то оно, как известно, будет совпадать со всем отрезком [0, 1].

Краевая задача (10е0), (11) представляет собой первую начально-краевую задачу относительно функции w = Би для линейного псевдопараболического уравнения третьего порядка. Заметим, что при принадлежности функции и 0 (х) пространству Ж2 (О) функция Б(х, 0, и0) также будет принадлежать тому же пространству — это следует из условия (7). Принадлежность начальной функции пространству Ж2 (О), функции g(x, 0 пространству Ь 2(0) и условия (4)-(6) гарантируют нам разрешимость данной задачи в пространстве V 2

[11, 12]. Далее, из условия взаимной однозначности оператора Б и вновь из условия (7)

вытекает, что функция и(х, 0 однозначно находится как решение уравнения

и что она будет принадлежать пространству V2. Следовательно, число 0 является элементом множества Л — то есть множество Л не пусто.

Доказательство открытости и замкнутости множества Л проводится с помощью априорной оценки решений краевой задачи (10 е л), (11) в пространстве V 2.

Анализируя последовательно равенства

\ \ ЬБ е лУ • wdxdт = II g • wdxdт , (12)

| | ЬБ,е, 1и • ^^Т = II g • wтdxdт , (13)

11 ЬБ,е, 1и • = II g • , (14)

I I ЬБ,е,1и • )т ^Т = Ц £ • (аХ^ )т ^Т (15)

и используя при этом условия (4)-(8), неравенство Юнга и второе основное неравенство для эллиптических операторов [13], получим, что для решений рассматриваемой краевой задачи будет выполняться неравенство

N1 ^ £ К1 [11,?1|Ь2(е) + l|B(x,0,u 0 11 Ж22(О) + N^(0,t;Ж22(О) + 11и11 Ь2(0,t;Ж22(О)], в котором постоянная К1 зависит лишь от области О, коэффициентов оператора Ь и от чисел а1з а2 и е . Вновь вследствие условия (7) от данного неравенства можно перейти к неравенству

и1 ^2 £ К2 [||8||Ь2(6) + ||У 0^ Ж22(О) + |М|Ь2(0, ПЖ22(О)];

используя же далее лемму Гронуолла, мы получим, что для функции w(x, 0 имеет место априорная оценка

v2 £ К0[|У ь2(о) + || и0 || Ж.?(О)] (16)

с постоянной К0 , зависящей от тех же величин, от которых зависит постоянная К1 , а также от

числа Т. Наконец, еще раз используя условие (7), мы придем к аналогичной оценке для

||и|^2 £ К0 [||8Ц Ь2(0) + К11ж22(О)]. (17)

С помощью оценок (16) и (17) мы и докажем открытость и замкнутость множества Л.

Пусть 10 есть элемент множества Л, 1 = 10 + 1. Покажем, что при малой величине 111 число 1 также будет принадлежать множеству Л.

Для произвольной функции у(^ 0 из пространства V 2 рассмотрим краевую задачу: найти решение уравнения

1Б,е,1 и = ^(Х’ 1) » ЯФ(Х’ *’ ^ (10е,Яо)

для которого выполняются условия (11). Из условий (4), (7) и (8) следует, что функция

Ф(х, I, V) будет принадлежать пространству Ь2 (0). Но тогда согласно определению множества Л краевая задача (10^), (11) будет иметь решение и(х, г), принадлежащее

пространству V2. Другими словами, данная краевая задача порождает оператор О,

переводящий пространство V2 в себя: О^) = и. Из оценки (17) и из условий (4), (7) и (8) следует, что для любых двух функций V 1(х, г) и v2(х, г) из пространства V2 имеет место неравенство

№ ,) — О^ 2)|| V, Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Au = II K(х, y, t, t)u(y, t)dtdy,

Au = | K1(х, y, t)u(y, t)dy + || K2(х, y, t, t)u(y, r)drdy .

Нетрудно привести и другие примеры.

1. Carlson D.E. Linear Thermoelas Ticity // Encyclopedia of Physics. Berlin, Springer, 1972.

2. Cannon J.R. The solution of the heat equation subject to the specification of energy // Quart. Appl. Math. 1963, V. 21,

3. Камынин Л.И. Об одной краевой задаче теории теплопроводимости с неклассическими граничными условиями // Журнал вычисл. матем. и мат. физики. 1964. Т. 4. № 6. С. 1006 — 1024.

4. Ионкин Н.И. Решение одной краевой задачи теории теплопроводимости с неклассическим краевым условием // Дифференц. уравнения. 1977. Т. 13. № 2. С 294 — 304.

5. Cannon J.R., Van der Hoek J. The classical solution of the one-dimensional two-phase Stefan problem with energy specification // Ann. Math. Pura ed Appl. 1982. V. 130. P. 385 — 398.

6. Cannon J.R., Van der Hoek J. The one — phase Stefan problem subject to the spesification of energy // J. Math. Anal.

and Appl. 1982. V. 86. N 1.P. 281 — 291.

7. Муравей Л.А., Филиновский А.В. Об одной нелокальной краевой задаче для параболического уравнения // Мат. заметки. 1993. Т. 54. № 4. С. 98 — 116.

8. Bouziani A., Benouor N.-E. Problem mixte avec conditions integrals pour une classe d’equations paraboliques // C. R. Acad. Sci. Paris. 1995. V. 321. Ser. I. P. 1177 — 1182.

9. Иванчов Н.И. Краевые задачи для параболического уравнения с интегральными условиями // Дифференц. уравнения. 2004. Т. 40. № 4. С. 547 — 564.

10. Fridman A. Monotonic decay of solutions of parabolic equations with nonlocal boundary conditions // Quat. of Appl. Math. 1986. V. XLIV. N 3. P. 401 — 407.

11. Якубов С.Я. Линейные дифференциально-операторные уравнения и их приложения. Баку: Элм, 1995.

12. Kozhanov A.I. Composite Type Equations and Inverse Problems // Utrecht: VSP, 1999.

13. Ладыженская О.А., Уральцева Н.Н. Линейные и квазилинейные уравнения эллиптического типа. М.: Наука, 1973.

14. Ладыженская О.А., Солонников В.А., Уральцева Н.Н. Линейные и квазилинейные уравнения параболического типа. М.: Наука, 1967.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, код проекта 03-01-00819.

Краевая задача с интегродифференциальным граничным условием для линейных параболических уравнений Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Кожанов Александр Иванович

Для параболических уравнений второго порядка рассматривается начально-краевая задача с граничным условием, сочетающим в себе условия задачи с «косой» производной и задачи с нелокальным граничным условием интегрального вида. Доказывается существование и единственность регулярных решений .

Текст научной работы на тему «Краевая задача с интегродифференциальным граничным условием для линейных параболических уравнений»

РАЗРЕШИМОСТЬ ЗАДАЧИ ТРИКОМИ ДЛЯ НЕКОТОРЫХ КЛАССОВ МНОГОМЕРНЫХ СМЕШАННО ГИПЕРБОЛО-ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ Н, А, Оршубеков

Теория краевых задач для гиперболо-параболических уравнений на плоскости хорошо изучены [1]. Насколько нам известно, их многомерные аналоги исследованы мало [2]. Пусть De — конечная область евклидова пространства Em+i точек (x, • • •, xm, t), ограниченная в полупространстве t > 0 конусами Ke : |x| = t + е, K ■ |x| = 1— t, 0 0 и t 0,

Axu — ut + J2 Mx,t)uXi + e(x,t), t 0, 0 m — 1, то ряд

а также ряды, полученные из него дифференцированием порядка p ^

Через akn(r,t), akn(r,t), ЪЩr,t), сЩr,t), dkn(r,t), то — 1 >.

Пусть сч(х,г), ь(х, г), с(х,г) е т+ 1, при этом ¿г<х, 0) = е(х, 0) = 0, £ 1.

Известно [3], что спектр оператора 6 состоит из собственных чисел = п(п + т — 2), п = ОД. каждому го которых соответствует кп ортонормированных собственных функций УП,т(в). При £ ^ —0 на £е получим функциональное соотношение между т(т, в) и Дт, в) вида

Искомое решение задачи Т в области будем искать в виде

«мд) = ^]ТиП( мжкт в), (в)

где т, ¿) — функции, подлежащие определению. Подставив (6) в (4), умножив затем полученное выражение на Дв) ф 0 и проинтегрировав по единичной сфере Н, для пП получим 5

Роии + I г Ро + 2-Ао ) м0г + ьоиог + сомо

Е Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

N^ — нормаль к прямой £ = п в точке £1 = пъ направленная в сторону полуплоскости п ^ £• Далее, из (2), (16) получим

Решение уравнения (15) записывается в виде [9] «

§ 1 = п+ ■Цг11, 5*2 = -П — С£п, С|„ — произволь-

ные независимые постоянные. Подставляя (18) в (19), для Скп, С|п получим систему уравнений

из которой найдем

(Q)- -Sv£(£Д d^ = АП = const.

Из (17), (19), учитывая условие (16), будем иметь 5

источники:

http://cyberleninka.ru/article/n/o-razreshimosti-kraevoy-zadachi-s-nelokalnym-granichnym-usloviem-dlya-lineynyh-parabolicheskih-uravneniy

http://cyberleninka.ru/article/n/kraevaya-zadacha-s-integrodifferentsialnym-granichnym-usloviem-dlya-lineynyh-parabolicheskih-uravneniy