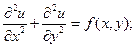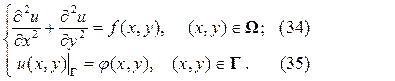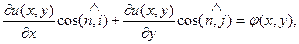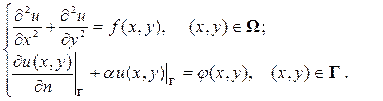Краевые задачи для эллиптических уравнений

Постановка задачи для уравнения эллиптического типа

Классическим примером уравнения эллиптического типа является уравнение Пуассона

или уравнение Лапласа, 0,

которое получается из уравнения Пуассона при f(x, t) º 0.

Здесь функция u(x, t) может иметь различный физический смысл, например, описывать стационарное, независящее от времени распределение температуры, скорость потенциального (безвихревого) течения идеальной (без трения и теплопроводности) жидкости, распределение напряжённостей электрического и магнитного полей, распределение потенциала поля тяготения и т.п.

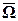
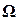
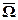
Первая краевая задача. Если на границе Г расчётной области = + Г (в данном случае расчётная область – это сама область , включая её границу Г) задана искомая функция, то соответствующая первая краевая задача для уравнения Лапласа или Пуассона называется задачей Дирихле:

Вторая краевая задача. Если на границе Г расчётной области 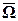задаётся нормальная производная искомой функции, то соответствующая вторая краевая задача называется задачей Неймана для уравнения Лапласа или Пуассона:

здесь n — направление внешней к границе Г нормали.

Иногда краевое условие (37) записывают в более удобном виде:

где 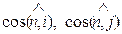— направляющие косинусы внешнего вектора единичной нормали к границе Г, i и j орты базисных векторов.

Третья краевая задача для уравнения Пуассона (Лапласа) имеет вид:

Замечание. Следует отметить, что в вышеперечисленных постановках задач математической физики число начальных условий равно порядку дифференциального уравнения по времени, а старший порядок производной по времени в начальных условиях на единицу меньше порядка дифференциального уравнения по времени.

Старший порядок производной по пространственной переменной в краевых условиях равен порядку дифференциального уравнения по пространственной переменной минус единица.

В одномерных задачах с одной пространственной переменной количество граничных условий точно равно порядку дифференциального уравнения по пространственной переменной.

Количество краевых условий для многомерных задач не ограничено, поскольку на разных участках границы могут быть заданы граничные условия различного рода.

Заключение (план — аннотация лекции №27).

Лекция 27 посвящена введению в приближённые методы решения дифференциальных уравнений с частными производными.

Отмечено, что при математическом анализе физических процессов, когда исследуемые свойства объекта описываются функциями не одной, а несколькими переменными, то при составлении математических моделей изучаемых явлений вместо обыкновенных дифференциальных уравнений возникают уравнения с частными производными.

В качестве примеров уравнений математической физики, наиболее востребованных на практике, рассмотрены уравнение Лапласа, уравнение Пуассона, уравнение теплопроводности (Фурье), волновое уравнение, уравнение Гельмгольца, телеграфное уравнение, уравнение переноса, уравнение акустики.

Приведена классификация уравнений с частными производными второго порядка, в основу которой положен анализ знака дискриминанта обобщённого уравнения второго порядка с частными производными.

Дана классификация методов решения уравнений с частными производными.

Обсуждаются подходы к постановке задач для уравнений математической физики. При этом корректность постановки задач связываемая с требованиями разрешимости; однозначности; непрерывной зависимости от исходных данных (иначе, устойчивости).

Рассмотрены примеры постановки задач для уравнений математической физики гиперболического, параболического и эллиптического типов.

1. И.С. Березин, Н.П. Жидков. Методы вычислений. Т. 2. – М.: Физматгиз, 1962. – 620 с.

2. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.

3. В.Ф. Формалёв, Д.Л. Ревизников. Численные методы. – М.: Физматлит, 2004. 400 с.

4. Б.П. Демидович, И.А. Марон, Э.З. Шувалова. Численные методы анализа.
– М.: Наука, 1967. – 368 с.

5. Н.В. Копчёнова, И.А. Марон. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 368 с.

Численные методы решения уравнений эллиптического типа

Введение

Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.

Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения опреде­ляется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]

Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.

Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:

(1)

где x – координата; u(x) – искомая функция; A(x), f(x) – некоторые непрерывные функции координаты.

Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:

(2)

Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:

(3)

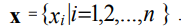
Граничные условия первого рода (условия Дирихле) для рассматривае­мой задачи могут быть представлены в виде:

(4)

где х1, xn – координаты граничных точек области [xmin, xmax]; g1, g2 – некоторые
константы.

Граничные условия второго рода (условия Неймана) для рассматривае­мой задачи могут быть представлены в виде:

(5)

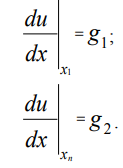
Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, по­лучим:

(6)

где u1, un – значения функции u(x) в точках x1, xn соответственно.

Проводя дискретизацию граничных условий Неймана на сетке (3), по­лучим:

(7)

Проводя дискретизацию уравнения (2) для внутренних точек сетки, по­лучим:

(8)

где ui, fi – значения функций u(x), f(x) в точке сетки с координатой xi.

Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n – 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].

Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) – (5) на координатной сетке (3).

Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve(a,b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице . Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:

Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии

(9)

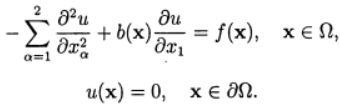
Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:

(10)

Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:

(10)

Метод релаксации соответствует использованию итерационного метода:

(11)

При \ говорят о верхней релаксации, при — о нижней релаксации.

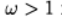
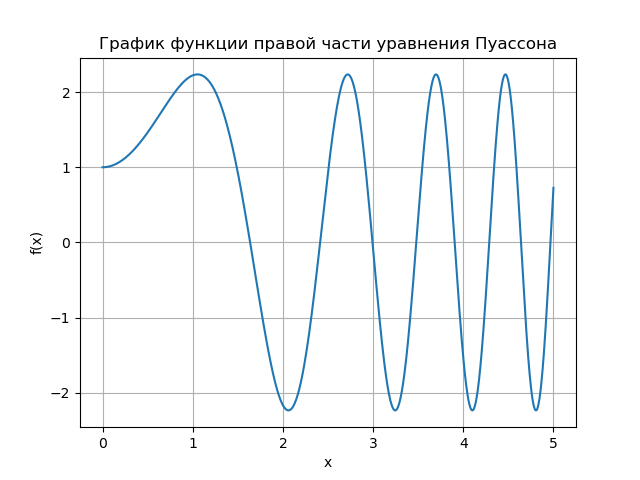
На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b(х) = 0) и уравнения конвекции-диффузии (b(х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при .

1. Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
2. Показано что метод релаксации имеет оптимальный диапазон () параметра релаксации.

Ссылки:

1. Рындин Е.А. Методы решения задач математической физики. – Таганрог:
   Изд-во ТРТУ, 2003. – 120 с.
2. Вабищевич П.Н.Численные методы: Вычислительный практикум. — М.: Книжный дом
   «ЛИБРОКОМ», 2010. — 320 с.

РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ОДНОГО ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Акимов А.А., Юраш Ю.С., Сафаргалина Э.И.

В статье рассматриваются краевая задача для сингулярного эллиптического уравнения . Доказывается теорема существования решения поставленной краевой задачи в классе гладких функций.

Похожие темы научных работ по математике , автор научной работы — Акимов А.А., Юраш Ю.С., Сафаргалина Э.И.

SOLUTION OF THE BOUNDARY-VALUE PROBLEM FOR SOME ELLIPTIC EQUATION

The article deals with a boundary value problem for a singular elliptic equation . An existence theorem is proved for the solution of the stated boundary value problem in the class of smooth functions.

Текст научной работы на тему «РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ОДНОГО ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ»

РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ОДНОГО ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ

Стерлитамакский филиал Башкирского государственного Университета

Юраш Ю.С. Сафаргалина Э.И.

Стерлитамакский филиал Башкирского государственного Университета

SOLUTION OF THE BOUNDARY-VALUE PROBLEM FOR SOME ELLIPTIC EQUATION

Ph.D., associate professor Sterlitamak branch Bashkir State University

Yurash Yu., Safargalina E. students

Sterlitamak branch Bashkir State University

В статье рассматриваются краевая задача для сингулярного эллиптического уравнения. Доказывается теорема существования решения поставленной краевой задачи в классе гладких функций. Abstract

The article deals with a boundary value problem for a singular elliptic equation. An existence theorem is proved for the solution of the stated boundary value problem in the class of smooth functions.

Ключевые слова: краевая задача, эллиптическое уравнение, функция Бесселя, функция Грина. Keywords: boundary value problem, elliptic equation, Bessel function, Green function.

В данной работе рассмотрено уравнение эллиптического типа

Su + Яu = U + U, + PU + Я = 0, (1)

где p,XeR , в области эллиптичности D — бесконечной полосе, ограниченной прямыми x = 0, x = 1 и y = 0 .

Для уравнения (1) при p > 1, Я 1

Я 1 r(x) е C[0;1]n C2 (0;1), г(1)= 0, то существует решение задачи (2) — (6) при

p > 1, Я 1. Л 1 и Л 0 и ограниченной

линией X = 0. Была построена теория потенциала уравнения (1) при X = 0 и получена формула решения через функцию Грина. Для полукруга построена функция Грина и в явном виде выписано решение задачи.

В работе [3] для уравнения (7) при 0 0, y > 0> построено решение краевой задачи с нелокальным условием на

линии y = 0 в виде суммы биортогонального ряда. Решение этой задачи использовалось при построении решения задачи Трикоми.

В данной работе используется спектральный метод для решения задачи (8) — (12) при p ^ 1 и

X Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

z2Z» + zZ’+ (z2 — v2)Z = 0,

где V = ^V(1 — P)2 = 1P — 1 = 1 (P — 1) при P > 1 Записывая общее решение уравнения Бесселя в виде

Z = C Jv (z) + C2^v (z),

где J — функция Бесселя первого рода, Yv — функция Бесселя второго рода, С и С2 — постоянные, получим общее решение уравнения (17) в виде

X (x) = x-v [CJV (ox) + C2Yv oo], v = P-1 (19)

Так как функция Y (o) при X —>■ 0 обращается в бесконечность, то ограниченным на [0;l] решением уравнения (17) будет функция (19) при С2 = 0 , то есть

X(X) = С1X 2 JP-1 (ox) • (20)

Найдём общее решение уравнения (18). Составим характеристическое уравнение, соответствующее уравнению (18):

к2 + (Л-о2) = 0 ^ к = ±д/(о2 -Л),

где О — Л > 0 , т.к. Л 0 положительны и счетны [9, с. 266], то обозначим

через /Лп, п е N — П -ый положительный корень функции

Итак, система функций

где Мп — положительный вещественный корень бесселевой функции ^ р_\ () , является системой твенн

собственных функций спектральной задачи (17), (21), соответствующей множеству собственных значений

Из вышеизложенных результатов следует, что функция

Un(x,У) = x 2 Jp_i(M„x)e-М

удовлетворяет условиям (9) — (11).

Решение задачи (8) — (12) будем искать в виде суммы ряда

u(x,У) = XCnun(x,У)=XCnx 2 Jp-1 (finx)e-Mn

где С — неизвестные пока коэффициенты.

Покажем, что функция u(x; y), определяемая формулой (23), удовлетворяет условию (12) и принадлежит классу (8) краевой задачи.

Удовлетворяя (23) граничному условию (12), имеем

т(x) = xcnx 2 jp-1 (Мп*), 0 —. В нашем случае V =-> 0 при р ^ 1.

Обоснуем равномерную сходимость ряда в правой части (24′) к функции f (х) на [0;1]. Имеет место утверждение [9, с. 288]

Утверждение. Если f (х) определена и дважды дифференцируема на [0;1], /(0) = f (0) = 0, f (1) = 0, f (х) ограничена, то

|С1 1. Очевидно, в этом случае У(о) = 0,

■x 2 t(x) + x 2 Т (x)

——1 limT(x) = ——1 limT (x) • x

2 x—0 3-P 3 — Px—0 V 7

если г(x) дифференцируемая функция на [0;1).

Лемма 2. Если р > 1. г(x)е С[0;1]п С2 (0;1). г(1)= 0 , то коэффициенты (19) удовлетворяют неравенству (26).

При наличии оценки (26) ряд в правой части формулы (24′) сходится абсолютно и равномерно на [0;1] [9, с. 282]. Следовательно, при выполнении условий лемм 1 и 2 относительно г(X) имеет место равенство (24), значит, функция и(X; у), определяемая формулой (23), удовлетворяет краевому условию (12).

,(x, у) 1 г(х)е С[0;1]^ С2 (0;1), т(1)= 0, то существует решение задачи (8) — (12) при р > 1, Я Надоели баннеры? Вы всегда можете отключить рекламу.