Постановка задачи для уравнения параболического типа
Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). Как отмечалось выше, в одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид:
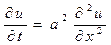
Уравнение (15), например, может описывать распространение тепла в тонком стержне длиной l, теплоизолированном по боковой поверхности. При этом функция u(x, t) задаёт значение температуры в любой точке стержня в произвольный момент времени t, при условии, что известно распределение температуры в стержне в начальный момент времени t = 0 и известна температура на концах стержня x = 0 и x = l в любой момент времени t. Таким образом, постановка задач для уравнения теплопроводности имеет следующий вид.
Первая начально-краевая задача. Если на границах стержня x = 0 и x = l заданы краевые условия первого рода, т.е. для любых моментов времени на концах стержня x = 0 и x = l заданы значения искомой функции u(x,t) (т.е. температуры):
и, кроме того, для функции u(x, t) заданы начальные условия, т.е. задано распределение температуры в любой точке стержня в момент времени t = 0:
то задачу (15) – (17) называют первой начально-краевой задачей для уравнения теплопроводности.
В терминах теории теплообмена функция u(x,t) описывает распределение температуры в пространственно-временной области W´T = <0 £ x £ l, 0 £ t £ T>, параметр а 2 – является коэффициентом температуропроводности, а краевые условия (16), (17) с помощью функций j 1(t) и j 2(t) задают температуру на границах
x = 0, x = l для различных моментов времени.
Вторая начально-краевая задача. Если на границах x = 0 и x = l заданы краевые условия второго рода, т.е. для x = 0 и x = l заданы значения производных искомой функции по пространственной переменной:
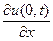
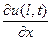
и, кроме того, для функции u(x, t) заданы начальные условия (21), то задачу (15), (19) – (21) называют второй начально-краевой задачей для уравнения теплопроводности. В терминах теории теплообмена граничные условия (19), (20) задают тепловые потоки на концах стрежня для различных моментов времени.
Третья начально-краевая задача. Если на границах x = 0 и x = l заданы краевые условия третьего рода, т.е. для x = 0 и x = l заданы линейные комбинации искомой функции и её частной производной по пространственной переменной:
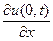
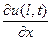
и, для функции u(x, t) заданы начальные условия (21), то задачу (15), (22), (23) называют третьей начально-краевой задачей для уравнения теплопроводности.
В терминах теории теплообмена граничные условия (22), (23) задают теплообмен между газообразной и жидкой средой (которые располагаются с разных «торцов» стержня) и границами расчётной области (т.е. внутренней частью стержня). Из-за теплообмена, температуры u(0, t) и u(l, t) на торцах стержня не известны, а известно, что температуры газообразной и жидкой среды соответственно равны
j 1(t)/a и j 2(t)/b. Параметры a и b являются коэффициентами теплообмена между газообразной или жидкой средой и соответствующей границей стержня.
Дата добавления: 2015-09-14 ; просмотров: 1245 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Безусловная разрешимость краевых задач для параболических уравнений с разрывными коэффициентами Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Е. Ф. Шарин
Исследована безусловная разрешимость решений параболических уравнений в классах Гёльдера. Доказана безусловная разрешимость уравнения g
Похожие темы научных работ по математике , автор научной работы — Е. Ф. Шарин
Текст научной работы на тему «Безусловная разрешимость краевых задач для параболических уравнений с разрывными коэффициентами»
БЕЗУСЛОВНАЯ РАЗРЕШИМОСТЬ КРАЕВЫХ ЗАДАЧ ДЛЯ ПАРАБОЛИЧЕСКИХ УРАВНЕНИЙ С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ*)
Работа посвящена исследованию безусловной разрешимости краевых задач для параболических уравнений в классах Гёльдера с разрывными коэффициентами [1]. В работе [2] предлагается единообразный подход к построению моделей сопряжения различных физических процессов таких, как распространение тепла в неоднородных средах (задачи типа дифракции), взаимодействие фильтрационных и каналовых потоков жидкости (фильтрация в скважину) и др. В работах [3,4] устанавливается безусловная разрешимость краевых задач в гёльдеровских простанствах для некоторых классов уравнений параболического типа с меняющимся направлением времени с границей раздела, имитирующей противоположные спутные потоки. В настоящей работе рассматривается случай односторонних спутных потоков, на границе раздела которых выполняются общие условия согласования.
В работе, состоящей из двух частей, рассматривается уравнение
где д(х) = А, х > 0, и д(х) = В, х О, и(х,0) = ^(х), х Надоели баннеры? Вы всегда можете отключить рекламу.
http://cyberleninka.ru/article/n/bezuslovnaya-razreshimost-kraevyh-zadach-dlya-parabolicheskih-uravneniy-s-razryvnymi-koeffitsientami