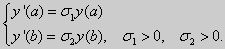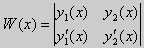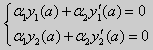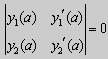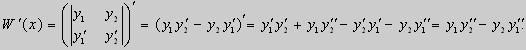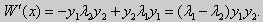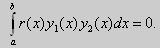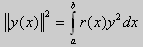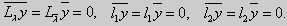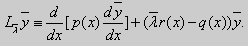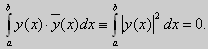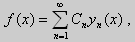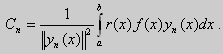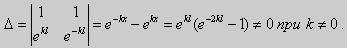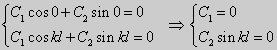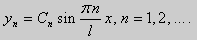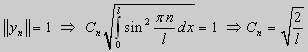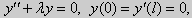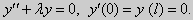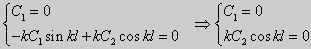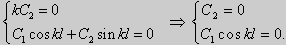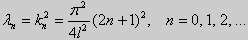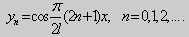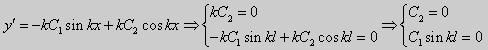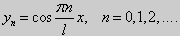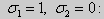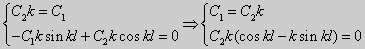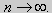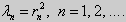Лекция 4. Краевые задачи для дифференциальных уравнений. Задача Штурма-Лиувилля.
Будем рассматривать однородное линейное уравнение второго порядка
Ly ≡ a2(x)y» + a1(x)y’ + a0(x)y = 0. Его можно записать по-другому:
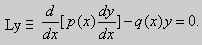 | (15) |
Однородное уравнение Ly = 0 и неоднородное Ly = f, как известно, имеют бесконечное множество решений. На практике часто бывает нужно из множества решений выделить только одно. Для этого задают некоторые дополнительные условия. Если это начальные условия у(х0) = уo, y'(xo) = y1, то получают задачу Коши. Если задают дополнительные условия на концах некоторого отрезка, то получают задачу, которая называется краевой задачей. Условия, которые задаются на концах отрезка, называются краевыми условиями. Краевые условия иногда именуют также граничными условиями и тогда говорят о граничной задаче.
Мы будем задавать линейные краевые условия вида
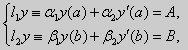 | (16) |
где α1, α2, β1, β2, A, B — заданные числа, причем по крайней мере одно из чисел α1, α2, и одно из чисел β1, β2, отличны от нуля. Если в (16) хотя бы одно из чисел А и В не равно нулю, то краевые условия называют неоднородными. Если А = В = 0, то условия (16) называются однородными. Краевая задача называется однородной, если рассматривается однородное уравнение (15) Ly = 0 и однородные краевые условия (16). Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям. Заметим сразу, что однородная краевая задача всегда имеет решение у ≡ 0 (тривиальное решение).
Наряду с уравнением (15) рассмотрим уравнение
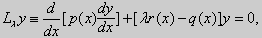 | (17) |
содержащее некоторый числовой параметр λ. Здесь функции р(х), q(x), r(x) действительные, а число λ может быть, вообще говоря, и комплексным. Краевая задача (17), (16) при А = В = 0 является однородной. Поэтому при любых λ она имеет тривиальное решение. Нас будут интересовать такие значения λ, при которых эта задача обладает не только тривиальными решениями.
Задача Штурма-Лиувилля. Найти те значения параметра λ, при которых уравнение (17) имеет нетривиальное решение, удовлетворяюшее однородным краевым условиям (16). В дальнейшем будем ее записывать в виде
Из множества краевых условий вида (16) ограничимся тремя частными случаями: 1) краевые условия первого рода 2) краевые условия второго рода 3) краевые условия третьего рода Общая задача Штурма-Лиувилля будет обладать свойствами, очень похожими на свойства в этих простых случаях, если на коэффициенты уравнения (17) наложить дополнительные условия: р(х), q(x), f(x) -непрерывные функции, причем р(х) имеет, кроме того, непрерывную производную на [а, b], р(х) > 0, q(x) ≥ 0. Основные свойства собственных значений и собственных функций задачи Штурма-Лиувилля. Лемма. Определитель Вронского двух собственных функций задачи Штурма-Лиувилля на концах отрезка [а, b] равен нулю. Доказательство. Напомним, что определителем Вронского функций у = y1(x) и у = у2(x) называется определитель вида Рассмотрим однородные краевые условия общего вида (16). Пусть у1(x) и у2(x) — две любые собственные функции. Это означает, что в точке x = а выполняются равенства Числа α1, и α2 не могут одновременно равняться нулю. Значит, алгебраическая система двух однородных уравнений с двумя неизвестными имеет ненулевое решение. Это возможно только в том случае, когда определитель этой системы равен нулю: Этот определитель совпадает с определителем Вронского в точке x = а, то есть W(a) = 0. Аналогичные рассуждения, проведенные для точки x = b, показывают, что W(b) = 0. Свойство 1. Две собственные функции задачи Штурма-Лиувилля, соответствующие одному и тому же собственному значению λ, линейно зависимые. Доказательство. Так как собственные функции являются решениями одного и того же однородного уравнения (17) (по условию число λ одно), то в случае их линейной независимости определитель Вронского не равен нулю ни в одной точке отрезка [а, b]. Это противоречит только что доказанной лемме. Следовательно, y1(x) и у2(x) — линейно зависимые функции. Свойство 2. Две собственные функции у1(x) и у2(x), соответствующие различным собственным значениям λ1 и λ2 (λ1 ≠ λ2), на отрезке [а, b] ортогональны. Доказательство этого свойства проведем для собственных функций такой задачи, в которой уравнение имеет вид (18). Составим определитель Вронского функций у1 и у2 и продифференцируем его: Так как у1 и у2 — решения уравнения (18) при λ = λ1 и λ = λ2, соответственно, то получим Проинтегрируем по отрезку [а, b] левую и правую части полученного равенства. С учетом леммы будем иметь Если уравнение, входящее в задачу Штурма-Лиувилля, имеет вид (17), где r(х) > 0 и r(x) 1, то под ортогональностью функций в этом случае подразумевают ортогональность с весом r(х): две функции y1(x) и у2(х) ортогональны на отрезке [а, b] с весом r(x), если Под нормой функции ||у(x)|| в этом случае также подразумевают весовую норму: Свойство 3. Собственные функции, соответствующие различным собственным значениям, образуют линейно независимую систему функций. Это утверждение вытекает из попарной ортогональности собственных функций, соответствующих различным собственным значениям (см. свойство 2). Свойство 4. Собственные значения задачи Штурма-Лиувилля действительные. Доказательство. Предположим, что задача Штурма-Лиувилля Здесь черта означает переход к комплексно сопряженному выражению. В нашем случае Значит число Отсюда следует, что у(x) ≡ 0 на [а, b]. Значит ни одно комплексное число λ не может быть собственным значением. Свойство 5. Пусть коэффициенты уравнения (17) удовлетворяют условиям: р(х), q(x), r(x) — непрерывные функции и, кроме того, р(х) имеет непрерывную производную на [а, b], р(х) > 0, q(x) > 0, r(х) > 0. Тогда задача Штурма-Лиувилля Теорема Стеклова.Всякая непрерывная функция f(x), удовлетворяющая однородным краевым условиям : l1f = 0 и l2f = 0 , и имеющая непрерывные производные до второго порядка на отрезке [а, b], разлагается на этом отрезке в сходящийся ряд Фурье по собственным функциям yn(х) задачи Штурма-Лиувилля где коэффициенты Фурье Сn вычисляются по формулам: Эта теорема применяется при решении уравнений математической физики методом Фурье. Решение задач Штурма-Лиувилля Вначале рассмотрим уравнение (18) y» + λy = 0. и краевые условия первого рода (19) y(a) = y(b) = 0. Для удобства будем считать, что a = 0 и b = l > 0. К такой задаче можно всегда свести данную задачу, если сделать замену переменной x’ = x — a, при этом вид уравнения не изменится. Вид общего решения уравнения (18) зависит от значений параметра λ. Разберем три случая: 1) λ 0. В первом случае обозначим λ = — k 2 . Тогда характеристическое уравнение r 2 — k 2 = 0 будет иметь действительные различные корни r1 = k, r2 = — k: Поэтому, общее решение дифференциального уравнения запишется в виде y = C1e kx + C2e -kx . Подставим краевые условия в общее решение и получим Следовательно, система имеет только нулевое (тривиальное) решение C1 = C2 = 0. Значит, при λ 2 и получим характеристическое уравнение r 2 + k 2 = 0. Оно имеет комплексные корни r1 = ki и r2 = -ki и общее решение дифференциального уравнения в этом случае запишется в виде y = C1cos kx + C2sin kx. Подставим краевые условия в общее решение: Для того, чтобы эта система имела нетривиальные решения, необходимо и достаточно, чтобы sin kl = 0. Следовательно kl = πn, то есть Обычно постоянный множитель выбирают либо равным единице, либо из условия нормировки: По тому же алгоритму решаются задачи Штурма-Лиувилля следующего вида: и Эти задачи так же, как и предыдущая, при λ 0 не имеют собственных значений. В случае λ > 0 общее решение уравнения записывается в виде y = C1cos kx +C2sin kx, где а) для задачи (23) Для того, чтобы эти системы уравнений имели нетривиальные решения, необходимо и достаточно, чтобы coskl = 0. Следовательно, Собственные функции задачи (23) имеют вид Некоторые отличия возникают при решении задачи Штурма-Лиувилля в случае краевых условий второго рода Рассуждениями, аналогичными тем, которые проводились для краевых условий первого рода, можно показать, что задача (25) при λ 0. В этом случае, общее решение уравнения имеет вид y = C1cos kx + C2sin kx, Эта алгебраическая система имеет нетривиальные решения тогда и только тогда, когда, sinkl = 0 то есть kl = πn или Для задачи Штурма-Лиувилля с краевыми условиями третьего рода (21) уже не удается получить собственные значения в явном виде. В качестве примера рассмотрим одну такую задачу, когда При Получившаяся алгебраическая система будет иметь нетривиальные решения только в том случае, когда coskl — ksinkl = 0 или Уравнение (28) является трансцендентным уравнением относительно k. Оно не решается в явном виде. Однако, построив графики левой и правой частей уравнения (28), видно, что оно имеет бесконечно много решений (см. рис.13). Обозначим корни уравнения (28) через rn, n = 1,2, . . Тогда Численными методами можно найти приближенные значения rn. Из системы (27) при k = rn получим C1n = rnC2n , где C2n -произвольные постоянные. При этих значениях постоянных решения дифференциального уравнения будут иметь вид Они являются собственными функциями краевой задачи (26) с собственными значениями Рассмотрим для простоты уравнение второго порядка Коэффициенты и будем считать непрерывными в некотором интервале . Тогда каждое решение уравнения (1) будет определено во всем этом интервале. В дальнейшем вместо уравнения (1) будем рассматривать уравнение вида Уравнения (1) и (2) могут быть преобразованы одно в другое. Уравнение вида (2) называются самосопряженными. Решение дифференциального уравнения полностью определяется начальными условиями . Однако во многих физических задачах приходится искать решения, заданные иным способом. Например, может быть поставлена задача: найти решение уравнения (2), принимающее в точках и заданные значения и . Обычно в таких случаях значения решения ищутся только для из . Таким образом, заданные значения и находятся на концах интервала, поэтому задачи такого рода называются краевыми (граничными) задачами . В дальнейшем мы положим в основу интервал (основной интервал), что не уменьшает общности рассуждений. Весьма общий вид краевых условий для уравнения второго порядка следующий: где — заданные постоянные, причем не равны одновременно нулю. Если , то краевые условия называются однородными , например: y'(0)=y'(\pi). \end Вообще говоря, краевые задачи не всегда разрешимы, т.е. не всегда существует такое решение, которое принимает требуемые значения на концах интервала. Например, краевая задача не имеет ни одного решения. Задача имеет ненулевое решение только для целочисленных значений . В самом деле, из общего решения дифференциального уравнения (4) вытекает, что краевые условия выполнимы в том и только в том случае, если есть квадрат целого числа . Соответствующими решениями являются функции . Как видно из этого примера, если в уравнении (2) есть функция параметра , то при известных условиях существуют такие значения параметра, для которых однородная краевая задача для уравнения (2) имеет ненулевое решение. Эти значения называются собственными значениями , а соответствующие им решения краевой задачи — собственными функциями . Последние определяются лишь с точностью до произвольного постоянного множителя. Так для краевой задачи , числа и функции являются соответственно собственными значениями и собственными функциями задачи. Наряду с простыми собственными значениями, когда одному собственному значению отвечает одна собственная функция (с точностью до постоянного множителя), существуют кратные собственные значения, когда собственному значению отвечают две или более линейно независимые собственные функции. При решении краевых задач (для линейных однородных дифференциальных уравнений) поступают так: находят общее решение данного дифференциального уравнения где — линейно независимые решения. Затем требуют, чтобы это решение удовлетворяло заданным граничным условиям. Это приводит к некоторой линейной системе уравнений для определения . Разрешая эту систему, если возможно, находят решение данной краевой задачи. При этом, если возникает задача о нахождении собственных значений, условие наличия ненулевого решения у системы, определяющей , является условием, определяющим собственные значения. Это бывает некоторое вообще трансцендентное уравнение для . Пример 1. Решить краевую задачу . Решение. Общее решение данного уравнения Полагая в (6) и в (5) и учитывая краевые условия, получаем для нахождения значений постоянных и неоднородную линейную систему Определитель этой системы следовательно, она имеет единственное решение Подставляя найденные значения и в (5), получаем решение заданной краевой задачи Пример 2. Найти собственные значения и собственные функции краевой задачи Решение. Обшее решение уравнения (7) Полагая (9) и в (10) и учитывая краевые условия (8), получаем для нахождения и однородную линейную систему Система (11) будет иметь ненулевые решения тогда и только тогда, когда ее определитель равен нулю; приравняв его нулю, получаем уравнение для нахождения собственных значений данной краевой задачи: Так как по условию , то , а значит собственные значения Им соответствуют (с точностью до постоянного множителя , который можно положить равным единице) собственные функции являющиеся решениями краевой задачи (7)–(8). Замечание. Собственные значения рассмотренных выше задач образуют возрастающую числовую последовательность. Если же коэффициенты дифференциального уравнения имеют особую точку на границе основной области или если основная область бесконечна, например вся числовая ось, то спектр, т.е. совокупность собственных значений, может обладать иной структурой. В частности, могут встретиться спектры, содержащие все числа какого-либо интервала значений , так называемые непрерывные спектры. Например, пусть требуется решить уравнение для интервала при «краевых условиях»: ограничено на бесконечности. Очевидно, в этом случае всякое неотрицательное число является собственным значением с собственными функциями и . При решении задач математической физики, приводящих к задачам на определение собственных значений, часто получаются дифференциальные уравнения вида но такие, что в концевых точках основной области могут иметь место особенности дифференциального уравнения, например, обращение в ноль коэффициента . Для этих особых точек из самого характера задачи возникают условия, например, непрерывности или ограниченности решения или обращение его в бесконечность не выше заданного порядка. Эти условия играют роль краевых условий. Типичным примером является уравнение Бесселя которое появляется в задачах математической физики. Здесь и сделанное выше предположение, что 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEoAAAAWBAMAAACVshfOAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAARHBm2bmQdAxgYJRILAORBKhAAABjklEQVQoz2NgIAVwHYDQ7nhVhUBpjQnoMpyFCGYSlMGehKaIt9ktAMZm3gBlMJqiqeJw4P0DY89XgLHCBFCdd76AwUIAyvaAMRj0C0DkFXOYgL8Aw3oFBk4TTecDjCZA/hQbFRsGBjGw3YJXUiHKGO0FGPYXMEjot+j+YfzNwMDzaH7mfgEGZgOIGVqtYGWM+UCzChhC9R8wJDN+Z2CQEJB3/CbAwGcItUo7C+RWxv9AVQsYas8HMH7mBKq6zlAfMJeBgTsR5kLVLpgqoCP8L3B+ZvoOEt4P0sz9EaZKtAvqLqCNjGYMrF9BNjIwdoBcArdRtRscOu8FGPwnMDB+YZBIArl+8qEvDFMYkFwPCcL4AgYzAQaezwxhE0Ahsf/obyZbYEgsAEveahWABIXaAqZsBgaWf08sGRh2CDCUuZStAIaoPjhxXGmFhapkSoQDMAASL0FiiPECIyg9HANLP4fHBaNOJChGHMCxDYt3Rmv0lMMI0hC/ECXBYKQcCDA2QU2FBVhVCaCm6KUM5AMA1j1dCL7zVu0AAAAASUVORK5CYII=» style=»vertical-align: middle;» /> во всей основной области здесь уже не выполняется, так как . Точка является особой точкой для уравнения Бесселя. Требование, чтобы решение было ограничено в этой точке, будет специального вида краевым условием для уравнения Бесселя: найти решение уравнения (12), ограниченное при и, например, обращающееся в ноль при . Пример 3. Решить краевую задачу функция ограничено при . Решение. Данное уравнение является уравнением Эйлера. Его общее решение имеет вид По условию решение должно быть ограниченным при . Это требование будет выполнено, если в общем решении положить . Тогда будем иметь . Краевое условие дает . Следовательно, искомое решение . Содержание лекций 1-го семестра годового спец. курса «Краевые задачи для систем обыкновенных дифференциальных уравнений». Tема 1. Однородные системы дифференциальных уравнений 1-го порядка. Векторное преставление задачи Коши. Теорема существования и единственности. Пространство решений однородной системы дифференциальных уравнений. Векторное представление задачи Коши. Некоторые сведения из линейной алгебры и анализа. Норма матрицы и некоторые неравенства, связанные с определением нормы. Краткие сведения о функциональных рядах. Теорема существования и единственности решения задачи Коши. Пространство решений однородной системы уравнений. Пространство решений однородного дифференциального уравнения высокого порядка. Тема 2. Однородные системы дифференциальных уравнений с постоянными коэффициентами. Задача Коши. Матричная экспонента, ее свойства и вычисление с использованием жордановой формы. Примеры построения фундаментальной матрицы решений. Задача Коши для однородной системы уравнений. Матричная экспонента. Тема 3. Линейные неоднородные системы дифференциальных уравнений. Теорема существования и единственности. Метод вариации произвольных постоянных. Формула Коши. Априорная оценка решения. Теорема существования и единственности. Линейные неоднородные дифференциальные уравнения высокого порядка. Априорная оценка решения задачи Коши. Тема 2. Непрерывная зависимость решения краевой задачи от параметров. Возмущенная краевая задача. Теорема о разрешимости возмущенной краевой задачи. Теорема о непрерывной зависимости решения краевой задачи от параметров. Понятие собственных чисел и собственных функций краевой задачи. Возмущенная краевая задача. Непрерывная зависимость решения от параметров. Понятие собственных чисел и собственных функций краевой задачи. Тема 3. Краевая задача на всей числовой прямой для системы уравнений уравнения высокого порядка с постоянными коэффициентами. Теорема существования и единственности, функции Грина. Краевые задачи на полупрямой для системы уравнений и уравнения высокого порядка с постоянными коэффициентами. Условия Лопатинского, функции Грина. Тема 4. Формальное определение матричной функции Грина как обобщенное решение краевой задачи для матричного уравнения. Дельта-функция. Физическая интерпретация решения. Пример определения матричной функции Грина краевой задачи на конечном отрезке. Физическая интерпретация функции Грина. Тема 1. Приведение двухточечной краевой задачи к серии задач Коши. Проблема «сплющивания» базисных решений. Метод ортогональной прогонки . Серии задач Коши в методе «стрельбы». Проблема «сплющивания» базисных решений. Пример некорректного применения метода стрельбы для решения хорошо обусловленной краевой задачи. Ортогонализация Грама-Шмидта. Метод ортогональной прогонки. Метод множественной стрельбы. Литература к 1-му семестру. 1. , Обыкновенные дифференциальные уравнения с постоянными коэффициентами. Издательство НГУ, 1994.-Т.1: Краевые задачи.- 264 с. 2. , Численные методы, Москва, Наука, 1975, 632 с. 4. Федорук дифференциальные уравнения, Москва, Наука, 1985, 448 с. 5. , Методические указания к курсу « Обыкновенные дифференциальные уравнения» , Новосибирск, НГУ, 1986, 26 с. 6. ., Линейные краевые задачи для систем обыкновенных дифференциальных уравнений на конечном отрезке, Методические указания, Новосибирск, НГУ, 1995, 34 с. Содержание лекций 2-го семестра годового спец. курса «Краевые задачи для систем обыкновенных дифференциальных уравнений». Тема 1. О численном исследовании решения нелинейной краевой задачи в зависимости от параметров модели. Множественность решений как типичное проявление нелинейности проблемы. Примеры нелинейных краевых задач с точным решением, иллюстрирующих природу множественности решений. Формулировки нелинейных краевых задач. Геометрическая интерпретация. Нелинейные эффекты, как отражение реальных физических процессов, моделируемых краевой задачей. О численном исследовании нелинейных краевых задач. Примеры нелинейных краевых задач, имеющих точное решение, которые иллюстрируют нелинейные эффекты. Множественность решений и петля гистерезиса. Тема 3. Метод стрельбы и метод множественной стрельбы. Метод Ньютона для решения системы нелинейных уравнений. Дифференцируемость решения задачи Коши по начальным данным и параметрам. Редукция краевой задачи к системе нелинейных уравнений относительно сеточных значений решения краевой задачи и её решение методом Ньютона. О решении системы нелинейных уравнений методом Ньютона. Дифференцируемость решения задачи Коши по начальным данным и параметрам. Метод стрельбы. Метод множественной стрельбы. Тема 1. Системы нелинейных уравнений с параметром. Теорема о неявной функции. Методы продолжения решения по параметру для построения гладкой пространственной кривой, определяемой системой нелинейных уравнений. Теорема о неявной функции. Применение метода Ньютона при продолжении решения по параметру. Продолжение решения по параметру как задача Коши. Тема 2. Продолжение решения по текущим параметрам для построения гладкой пространственной кривой, содержащий особые точки типа «поворот». Выбор текущего параметра с использованием параметризации. Продолжение решения по длине дуги. Метод Кубичека. Теорема о неявной функции и параметризация. Продолжение решения по текущему параметру. Численное построение интегральной кривой системы обыкновенных дифференциальных уравнений, представляющей зависимость решения системы нелинейных от параметра. Продолжение решения по длине дуги пространственной кривой, определяемой системой нелинейных уравнений. Метод Кубичека. Тема 1. Продолжение решения по параметру в методе множественной n1. Система нелинейных уравнений относительно сеточных значений решения, определенная на решениях серии задач Коши. n2. Серия задач Коши, необходимая для реализации метода продолжения по параметру. n3. Продолжение решения по параметру Тема 2. Дискретная модель нелинейной краевой задачи, основанная на сплайн-коллокации. n1. Метод сплайн-коллокации. n2. Формулировка дискретной модели. n3. Адаптация сетки. Tема 3. Дискретные модели нелинейных интегральных уравнений. n2. Использование интерполяционных кубических сплайнов класса C2 при формулировке дискретной модели нелинейного n3. Система линейных алгебраических уравнений, определяющая фундаментальные кубические сплайны. Тема 4. Численные примеры. n1. Модель пленочного электростатическое реле. n2. Стационарные режимы работы каталитического реактора с n3. Краевая задача, описывающая зависимость предельного цикла осциллятора Ван дер Поля от параметра. n4. Определение положения ударных волн при обтекании конуса сверхзвуковым потоком газа. Заключение. Демонстрация работы комплекса программ на примерах нелинейных краевых задач. Литература ко 2-му семестру. 7. , Обыкновенные дифференциальные уравнения с постоянными коэффициентами. Издательство НГУ, 1994.-Т.1: Краевые задачи.- 264 с. 8. , Численные методы, Москва, Наука, 1975, 632 с. 9. Методы анализа нелинейных динамических моделей, Москва, Мир, 1991, 368 с. сплайн-функций, Москва, Наука, 1980, 352 с 11., Программа численного решения нелинейных краевых задач для систем обыкновенных дифференциальных уравнений с параметром.// Вычислительные методы линейной алгебры. Новосибирск, Наука, Сибирское отделение, 1990, с.104-200. 12., . Применение продолжения по параметру на основе метода множественной стрельбы для численного исследования нелинейных краевых задач. // Сибирский журнал индустриальной математики, т. 4, N 1(7), (2001), c. c. 83-101. 13., , Нелинейные краевые задачи для систем обыкновенных дифференциальных уравнений на конечном отрезке. Учебное пособие./НГУ, Новосибирск, 2008,104 с. Характерные вопросы по темам годового спецкурса «Краевые задачи для систем обыкновенных дифференциальных уравнений». 1. Условия, определяющие матричную функцию Грина краевой задачи Понятие хорошей обусловленности. 2. Метод множественной стрельбы для решения нелинейной краевой задачи 1. Понятие хорошей обусловленности нелинейной краевой задачи Метод квазилинеаризции (метод Ньютона). 2.Условия, определяющие функцию Грина краевой задачи для уравнения высокого порядка Представление нелинейной краевой задачи в виде нелинейного интегрального уравнения. 1. Условия однозначной разрешимости линейной краевой задачи 2. Уравнения для вариаций задачи Коши для системы нелинейных дифференциальных уравнений. 1. Метод ортогональных прогонок решения линейной краевой задачи 2. Метод Кубичека для численного исследования зависимости решения системы нелинейных уравнений с параметром. 1. Использование интерполяционных кубических сплайнов при формулировке дискретной модели нелинейного интегрального уравнения. где 2. Метод продолжения решения с параметризацией для численного исследования зависимости решения системы нелинейных уравнений от параметра. 1.Использование метода сплайн-коллокации для построения дискретной модели нелинейной краевой задачи 2.Метод продолжения решения системы нелинейных уравнений по параметру как задача Коши. 1.Различные типы краевых условий линейной краевой задачи Привести выражения условий, определяющих соответствующие матричные функций Грина. 2. Формулировка краевой задачи, определяющей производную решения краевой задачи по параметру q. Применение метода множественной стрельбы для определения производной решения краевой задачи по параметру q. 1.Определить функцию Грина краевой задачи: Далее, записать интегральное представление краевой задачи Чем характеризуется зависимость решения краевой задачи от параметра q? 2. Теорема о неявной функции и параметризация в методе продолжения по параметру решения системы из n нелинейных уравнений 1. Метод стрельбы и метод множественной стрельбы решения краевой задачи 2. Продолжение по параметру решения системы из n нелинейных уравнений 1. Понятие «возмущенной» линейной краевой задачи. Теорема о непрерывной зависимости решения линейной краевой задачи от параметров. Использование теоремы в определении Ω-окрестности в методе Ньютона (квазилинеаризации) для решения нелинейной краевой задачи. 2. Примеры физической интерпретации множественности решения нелинейной краевой задачи с параметром. http://mathhelpplanet.com/static.php?p=kraevye-zadachi-dlya-uravnenii-vysshih-poryadkov http://pandia.ru/text/77/386/78823.php
Те значения параметра λ, при которых задача Штурма-Лиувилля имеет ненулевое решение, называются собственными значениями (собственными числами) задачи, а сами эти решения — собственными функциями. Задачу Штурма-Лиувилля называют также задачей на собственные значения. В силу однородности уравнения и краевых условий собственные функции задачи Штурма-Лиувилля определены с точностью до постоянного множителя. Это означает, что если y(х) -собственная функция при некотором значении λ, то произведение Cy(x), где С — произвольная постоянная, также является собственной функцией при том же значении параметра λ. В связи с этим часто в качестве собственной функции рассматривают нормированную функцию у <х), у которой ||у(х)|| = 1. Такая собственная функция определена, по существу, однозначно (с точностью до знака ±). Далее мы подробно изучим наиболее простой случай задачи Штурма-Лиувилля, когда уравнение имеет видy» + λy = 0. (18) y(a) = y(b) = 0, (19) y'(a) = y'(b) = 0, (20) (21) 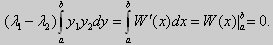
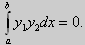
Функции y1(x) 0 и у2(х) 0, поэтому 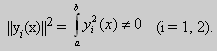
Значит, y1(x) и у2(х) на отрезке [а, b] ортогональны.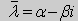
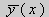
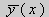
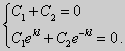
(22) 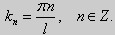
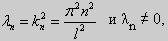
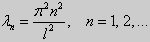
(23) (24) 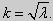
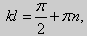
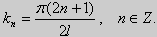
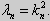
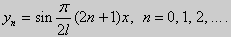
y» + λy = 0, y'(0) = y'(l) = 0. (25) 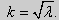
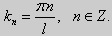
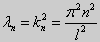
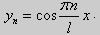
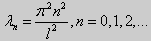
y» + λy = 0, y'(0) = y(0), y'(l) = 0. (26) 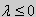
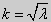
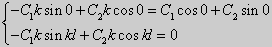
(27) ctgkl = k (28) 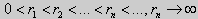
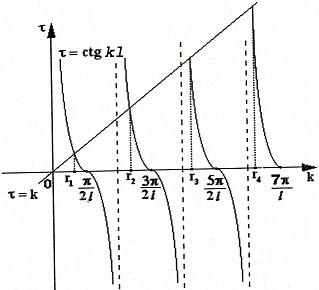
Рис.13Краевые задачи для уравнений высших порядков
«Краевые задачи для систем обыкновенных дифференциальных уравнений»
Раздел 1. Системы линейных дифференциальных уравнений первого порядка с переменными коэффициентами.
Раздел 2. Линейные краевые задачи.
Тема 1. Существование и единственность решения краевой задачи. Матричные функции Грина. Различные типы краевых условий. Краевая задача для дифференциального уравнения высокого порядка. Функции Грина. Вводные замечания. Существование и единственность решения краевой задачи. Различные случаи задания краевых условий. Краевые задачи для линейного дифференциального уравнения высокого порядка. Примеры построения функций Грина.

Раздел 3. О численных методах решения линейных краевых задач.
Тема 2. Метод множественной стрельбы как вариант ортогональной прогонки. Метод стрельбы и проблема сплющивания базисных решений
Раздел 4. Нелинейные краевые задачи на конечном отрезке.
Тема 2. Численное решений нелинейных краевых задач методом Ньютона (методом квазилинеаризации). Определение хорошей обусловленности нелинейной краевой задачи. Теорема о сходимости итераций по методу Ньютона. Определение хорошей обусловленности нелинейной краевой задачи. Метод Ньютона. Определение Ω-окрестности решения. Квадратичная сходимость итераций.
Раздел 5. Численное исследование решения системы нелинейных уравнений в зависимости от параметра
Раздел 6.Численное исследование решения нелинейных краевых задач. Метод продолжения решения по параметру
n1. Примеры представления нелинейной краевой задачи в виде
нелинейного интегрального уравнения с использованием
функции Грина.


Метод множественной стрельбы.