Теорема Кронекера-Капелли
Совместная система линейных уравнений имеет единственное решение, если ранг этой системы равен количеству переменных.
Совместная система линейных уравнений имеет бесконечное множество решений, если ранг этой системы меньше количества переменных.
Пример №1 . Исследовать систему алгебраических уравнений (без непосредственного решения системы) с помощью теоремы Кронекера-Капелли.
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:
Добавим 2-ую строку к 1-ой:
Добавим 3-ую строку к 2-ой:
Умножим 3-ую строку на (2). Добавим 4-ую строку к 3-ой:
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Добавим 2-ую строку к 1-ой:
Это соответствует системе:
-3x2 + 9x3 = 6
-4x1 + 5x2 + 7x3 — 10x4 = 0
За базисные переменные примем x1 и x2. Тогда свободные x3,x4.
Ранг основной матрицы равен 2. Ранг расширенной матрицы тоже равен 2. Система совместна и имеет бесконечное множество решений.
Пример №2 .
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Умножим 3-ую строку на (3). Умножим 4-ую строку на (-2). Добавим 4-ую строку к 3-ой:
Добавим 2-ую строку к 1-ой:
Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Добавим 2-ую строку к 1-ой:
3x2 -2x3 – 3x4 = 10
3x1 -x2 -2x3 = 1
Необходимо переменные x3,x4 принять в качестве свободных переменных и через них выразить базисные – x1, x2.
Ранг основной матрицы равен 2. Ранг расширенной матрицы тоже равен 2. Система совместна и имеет бесконечное множество решений.
Пример №3 . Дана система линейных уравнений у которой число уравнений равно числу неизвестных. При каком условии эта система имеет единственное решение?
Ответ: Система имеет единственное решение, если ранг этой системы будет равен количеству переменных.
Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи». В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $\widetilde$.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $\rang A=\rang\widetilde$.
Следствие из теоремы Кронекера-Капелли
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Исследовать СЛАУ $ \left \ <\begin
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $\widetilde$, запишем их:
Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $\Delta A$. Для вычисления определителя применим формулу №2 из темы «Формулы для вычисления определителей второго и третьего порядков»:
$$ \Delta A=\left| \begin
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $\rang A=3$.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $\Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $\Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $\Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Способ №2. Вычисление ранга методом элементарных преобразований.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
$$ \left( \begin
Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $\rang\widetilde=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $\rang=2$.
Ответ: система несовместна.
Приводим расширенную матрицу системы к ступенчатому виду:
$$ \left( \begin
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $\rang\widetilde=\rang\lt
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Критерий совместности системы линейных уравнений.
Критерий совместности системы линейных уравнений даёт теорема Кронекера-Капелли.
Леопольд Кронекер (1823 – 1891 гг.) ─ немецкий математик. Теорема, о которой пойдёт речь, содержалась в его лекциях, читавших в Берлинском университете в 1883 – 1891 гг.
Альфред Капели (1858 – 1916) ─ итальянский математик. Он, по-видимому, впервые дал формулировку теоремы с использованием термина «ранг матрицы» в своей работе в 1892г.
Теорема Кронекера-Капелли.
Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.
Пример. Исследовать систему на совместность
Решение. Приведение матрицы системы и расширенной матрицы системы к ступенчатому виду будем выполнять одновременно.

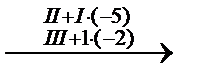



Ранг матрицы системы равен 2, а ранг расширенной матрицы системы равен 3. По теореме Кронекера-Капелли система несовместна.
Метод Гаусса решения системы линейных уравнений.
Метод Гаусса применяется для произвольной системы линейных уравнений. Нам понадобится
Определение. Систему линейных уравнений будем называть ступенчатой, если матрица этой системы ступенчатая.
При решении системы линейных уравнений применим следующий алгоритм:
1. Записываем расширенную матрицу системы (1) и приводим её к ступенчатому виду,
определяем ранги матрицы и расширенной матрицы системы.
2. Если найденные ранги не равны, то система несовместна.
3. Ранг матрицы системы равен рангу расширенной матрицы системы и равен числу r. В
этом случае система совместна и надо найти её решение.
4. Используя ступенчатый вид расширенной матрицы системы, записываем соответствующую ступенчатую систему.
5. Если число r равно числу неизвестных n, то ступенчатая система имеет вид
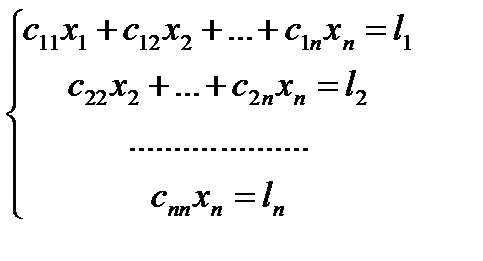
Из системы (2) последовательно находим значения для х1, х2,…, хт, начиная с последнего уравнения. В этом случае система (1) имеет единственное решение.
6. Если число r меньше числа неизвестных, то ступенчатая система имеет вид

В системе (3) r уравнений и n неизвестных. Неизвестные х1,…,хj1, которые первыми встречаются в уравнениях системы (3), назовём главными неизвестными, остальные ─ свободными неизвестными. Из системы (3) последовательно выражаем главные неизвестные через свободные, начиная с последнего уравнения. Свободные неизвестные могут принимать любые значения. В этом случае система имеет бесконечно много решений.
Примеры.
1). 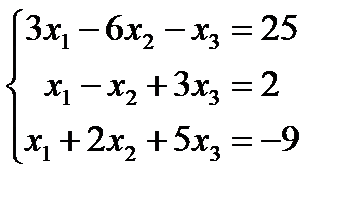
2) 
3) 
Правило Крамера решения систем линейных уравнений.
Габриэль Крамер (1704 – 1752) ─ швейцарский математик, который в 1750 г. нашёл метод решения систем линейных уравнений, названный впоследствии правилом Крамера.
Определение. Система линейных уравнений называется крамеровской,если тело уравнений равно числу неизвестных и определитель матрицы системы отличен от нуля.
Теорема 7.1. Крамеровская система имеет единственное решение, которое находится по формулам
где 



Доказательство. Пусть дана крамеровская система
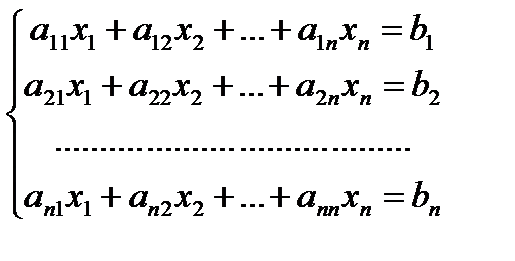
│А│= ∆ = 
По теореме 3 лекции 6 матрица системы А имеет обратную матрицу А -1 .
Запишем крамеровскую систему (4) в матричном виде
А = 
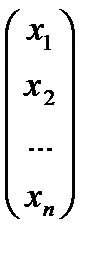
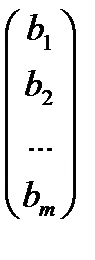
Умножим обе части матричного уравнения (5) слева на А -1 :
Ввиду ассоциативности умножения матриц имеем
А -1 (АХ) = (А -1 А)Х = ЕТХ = Х.
Х = А -1 В ─ решение системы.
1) Покажем, что такое решение единственно. Предположим, что Х1 и Х2 ─ два решения матричного уравнения (5). Тогда АХ1 = В и АХ2 = В, откуда АХ1 = АХ2. Умножая обе чисти равенства на А -1 слева, имеем
Следовательно, система (4) имеет единственное решение.
2) Найдём решение системы (4). Из равенства Х = А -1 В имеем:


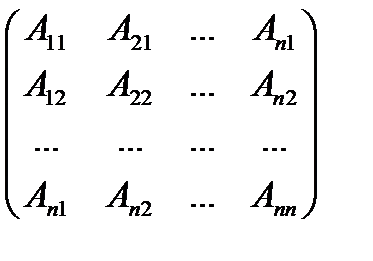







Обозначая определители в правой части равенств 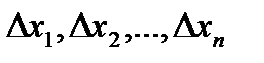

Пример. Решить систему уравнений по правилу Крамера

http://math1.ru/education/sys_lin_eq/kapelli.html
http://lektsia.com/3x3d30.html



