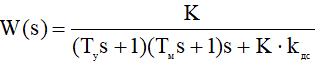Определение устойчивости систем автоматического управления промышленными роботами
Введение
Необходимым условием работоспособности системы автоматического управления (САУ), является её устойчивость. Под устойчивостью принято понимать свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов после прекращения их воздействия [1].
Постановка задачи
Теория просто и кратко
Анализ устойчивости системы по методу Михайлова сводится к построению характеристического многочлена замкнутой системы (знаменатель передаточной функции), комплексной частотной функции (характеристического вектора):
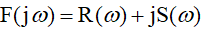
где 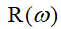
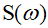
Замкнутая САУ устойчива, если комплексная частотная функция 
стрелки начало координат, проходя последовательно n квадрантов, где n – порядок характеристического уравнения системы, т. е.
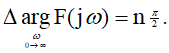
Рисунок 1. Амплитудно-фазовые характеристики (годографы) критерия Михайлова: а) – устойчивой системы; б) – неустойчивой системы (1, 2) и системы на границе устойчивости (3)
САУ электроприводом манипулятора промышленного робота (МПР)
Рисунок 2 – Структурная схема САУ электроприводом МПР
Передаточная функция данной САУ имеет следующее выражение [2]:
(3)
где kу – коэффициент усиления усилителя, kм – коэффициент пропорциональности частоты вращения двигателя величине напряжения на якоре, Tу – электромагнитная постоянная времени усилителя, Tм – электромеханическая постоянная времени двигателя с учётом инерции нагрузки (по своим динамическим характеристикам двигатель представляет собой передаточную функцию последовательно соединённых инерционного и интегрирующего звеньев), kдс – коэффициент пропорциональности между входной и выходной величинами датчика скорости, K – коэффициент усиления главной цепи: 
Численные значения в выражение передаточной функции следующие:
K = 100 град / (В∙с); kдс = 0,01 В / (град∙с); Tу = 0,01 с; Tм = 0,1с.
Далее запишем характеристический многочлен замкнутой системы
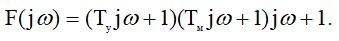

Решение на Python
Здесь следует отметить, что подобные задачи на Python ещё никто не решал, во всяком случае я не нашёл. Это было связано с ограниченными возможностями работы с комплексными числами. С появлением SymPy можно сделать следующее:
Где I мнимая единица, w- круговая частота, T1= Tу = 0.01 ,T2= Tм = 0.1
Получим развёрнутое выражение для многочлена:
Характеристический многочлен замкнутой системы –
-I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1
Сразу видим, что многочлен третьей степени. Теперь получим мнимую и действительную части в символьном отображении:
Действительная часть Re= -T1*w**2 — T2*w**2 + 1
Мнимая часть Im= -T1*T2*w**3 + w
Сразу видим вторую степень действительной части и третью мнимой. Подготовим данные для построения годографа Михайлова. Введём численные значения для T1 и T2, и будем менять частоту от 0 до 100 с шагом 0.1 и построим график:

Из графика не видно, то годограф начинается на действительной положительной оси. Нужно изменить масштабы осей. Приведу полный листинг программы:
Характеристический многочлен замкнутой системы — -I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1
Действительная часть Re= -T1*w**2 — T2*w**2 + 1
Мнимая часть Im= -T1*T2*w**3 + w
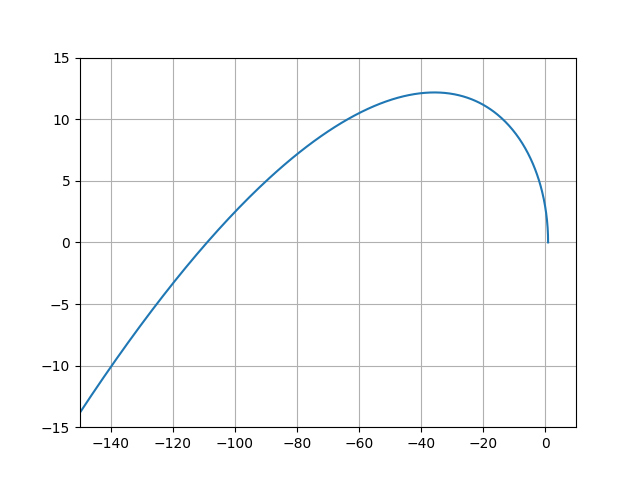
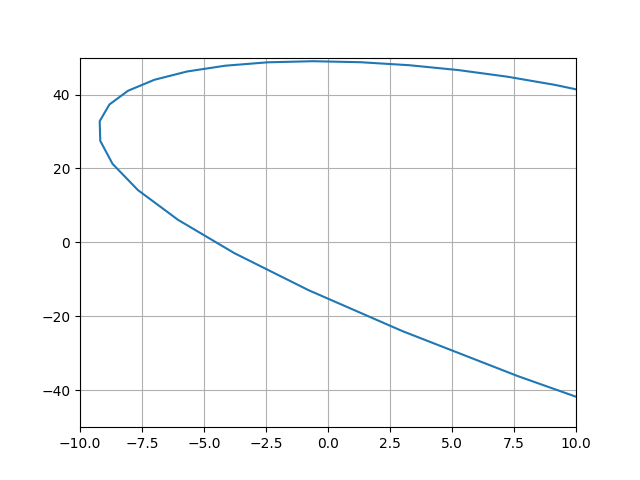
Теперь уже видно, что годограф начинается на действительной положительной оси. САУ устойчива, n=3, годограф совпадает с приведённым на первом рисунке.
Дополнительно убедится в том, что годограф начинается на действительной оси можно дополнив программу следующим кодом для w=0:
Начальная точка М(1,0)
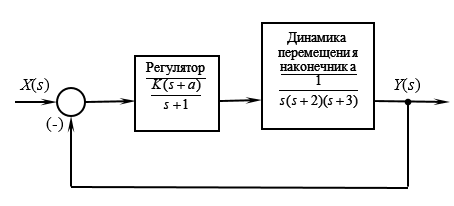
САУ сварочного робота
Рисунок 3. Структурная схема САУ позиционированием НСУ
Характеристическое уравнение данной САУ будет иметь вид [1]:

где K – варьируемый коэффициент усиления системы, a – определённая положительная константа. Численные значения: K = 40; a = 0,525.
Далее путём замены s на 

Решение на Python
Характеристический многочлен замкнутой системы — w**4 — 6*I*w**3 — 11*w**2 + 46*I*w + 21
Начальная точка М(21,0)
Действительная часть Re= w**4 — 11*w**2 + 21
Мнимая часть Im= -6*w**3 + 46*w
Построенный годограф Михайлова, начинаясь на вещественной положительной оси (М (21,0)), огибает в положительном направлении начало координат, проходя последовательно четыре квадранта, что соответствует порядку характеристического уравнения. Значит, данная САУ позиционированием НСУ – устойчива.
Выводы
При помощи модуля SymPy Python получен простой и наглядный инструмент для решения задач расчёта устойчивости систем автоматического управления, что является обязательным условием работоспособности любого промышленного робота и манипулятора.
Критерии устойчивости Рауса–Гурвица и Михайлова
(геометрический критерий устойчивости)
Пусть имеем линейное дифференциальное уравнение с постоянными вещественными коэффициентами:
Нулевое решение уравнения (1) асимптотически устойчиво, если все корни характеристического уравнения
имеют отрицательные вещественные части.
Критерий Рауса—Гурвица . Для того чтобы все корни уравнения (2) имели отрицательные вещественные части, необходимо и достаточно, чтобы были положительными все главные диагональные миноры матрицы Гурвица
Матрица Гурвица составляется так. По главной диагонали выписываются коэффициенты многочлена (2), начиная с и оканчивая . Столбцы состоят поочередно из коэффициентов только с нечетными или только с четными индексами, причем в число последних включается коэффициент . Все остальные элементы матрицы, отвечающие коэффициентам с индексами, большими или меньшими , полагаются равными нулю. Главные диагональные миноры матрицы Гурвица имеют вид
Таким образом, условие Гурвица гласит: для устойчивости решения уравнения (1) необходимо и достаточно, чтобы выполнялись соотношения
Так как , то условие 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEAAAAAUCAMAAAAKqMsNAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAEBeBQeekAcBcIdGCMHGRAmkNMgAAAQ1JREFUOMutVNuygyAMlIHcuCj//7UnWBGhasee5gEHJJvNZodp+lW4f+ZLlocZxvnjNmSgR/kRLLJpDTA8oyCg9THUosROLinIbN4PAUvZvahjomsKEuwI4bMtMuRl27POIF6rQBLQ9zPLsZxn3gko3J0KJNxBxJWBAtCmQPnY+0E4xuYVuwFAI/CBwnoPOQ0MXmNgqbB86wXfAKRqUBJcZa4UCslk1GVnLbDb8dPKIOUyzAmFtohFVbEwzwsOIrpeRDr4wGeuEbJSQK+Lg8EJwxjVyWoNLMuE+RiFQlA5sHNB9G8dYZAFVkmoD/2l9grSUiSaM0nTLOZcbBBty+D3T4M25sGmr/PJPLr+B9cTCgo80fp7AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> может быть заменено требованием 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAATBAMAAAAzNgPlAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAhgFdwNcQoTBBIfCwcRgyobwAAADiSURBVCjPY2AgD7DNwicrKuKGW1J5G8MRBTQx4wQYS7WAYd4EdB2BMOk+ARBiYBMpM0OWXgBh2Akw6DkwMKQWdb9A1u0OkZYDyjoxMIUwsGxCNpzTvQEmG8DA+5hB+wCK3ZxHGuB6VZ4x9F1AkeUqaYDbqxfEcK+BoY0N7npOFzBzngDDvAKQgnOKk6XvCkIlNaGu0gb614CBJ4D5CaviuoYpEEnmcKiPGLcxlCowcIUftD7MYMogDpGEhwZDqWEEyBEKbA0MhQzBYD2GcEkGDmE4O5jjWQHuGNnGFd5AcgoAAPGxMydfDSoLAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />.
Пример 1. Исследовать на устойчивость нулевое решение уравнения
Решение. Составляем характеристическое уравнение
Здесь . Выписываем диагональные миноры Гурвица
\Delta_4=\begin
\Delta_4>0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAASAAAAAUCAMAAAAawRC9AAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAYaQhwNaCBD4QkfCBxHFQI3bn4gAAAjJJREFUWMPtmNuSgyAMhg0BGg4jvP/TLlTaooJIZTp7yoWzu5Jvwp8Qsk7Tv50zUv+oI0PPOh0I/xSKeY8d3jcmpNDlnPwKlNqg0PAuhbUID6GLyn9PlLiGYpJqCmso6OtleM6+lKwDlK2iZC9K96LmgFJvR4VGTTWFlRWwJYOn2PY8lLIeUXIcSn8iqqmCco98yPibqfR5NQu7fiWTvyxl/QeiZAOlRHzNva0eSRA2L3Wd/PfZVeYESq2aZxXVGxVrRiXfjEreHV8KoyoR2CsYnvz5btkGRQ6HoYhGocKP2INaUvVUGJih4qTFmdoIzMtZf+ZdAxh7jOInUXam4v30BipWFPWgZKq8pDBOviWQrBXzGoWCUru7jJrCAuvfjMquUeEPgs6hZK7v65CW9uR4VoFz8p8rqQojREShcWHRDgZ9qCUqR8tscj2qsAT4foeFqNyCks/W5ZLChT3lBzTO7dHHxnUIhazHezIlC7aDDAhdQmELhW6X9gqqFZViEz+Jwvt5FPxhfjmkG4EUCLlp25w/HiYbOwootZ4xLqAQuBuACjURrr61QIeoUE25mZ1AYY6Sat/2GLB75TLDssLM7X4gGAxDrdrZBRQFjXKBGqiSrQQqDfXxHMu0iI7+xQnOhLezKKyjkOOquzSj0vWRJ1ZSdiO2UC2BWgZw8G4mYjQCFad+54egune4y3rQl5//LiDUwa6iDUFNWoOYx6DCfe6F/tSXSKAPoajnk+C4qL4A/qkkU6k3D1AAAAAASUVORK5CYII=» style=»vertical-align: middle;» />. Следовательно, тривиальное решение уравнения (5) асимптотически устойчиво.
Вычисление можно, например, организовать так. Составляем сначала старший минор Гурвица . По нему легко выписываются все младшие миноры . Затем начинаем вычислять последовательно и т.д. Если встретился отрицательный минор, решение неустойчиво и дальнейший подсчет не нужен.
Геометрический критерий устойчивости (критерий Михайлова)
Рассмотрим линейное дифференциальное уравнение n-го порядка с постоянными вещественными коэффициентами
Критерий устойчивости Михайлова
Устойчивость системы выясняется по характеристическому полиному передаточной функции:
где n – степень полинома.
Полагая p = j w , преобразуем характеристический полином в комплексный частотный полином:
D ( j ω ) = a 0 ( j ω ) n + a 1 ( j ω ) n -1 +…+ an -1 ( j ω ) + an .
В зависимости от степени числа ( j ω) n оно либо действительное, либо мнимое. По этой причине частотный полином распадается на действительную часть U ( ω) и мнимую часть V ( ω):
U ( ω) – четная функция ω, V ( ω) – нечетная функция ω. По этому признаку полиномы (5.8) и (5.9) можно назвать «четный» и «нечетный».
Задавая какое-либо значение частоты w 1 , из (5.8) и (5.9) получим числа U ( w 1 ) и V ( w 1 ) . Вместе они образуют комплексное число D ( j w 1 ) . На комплексной плоскости оно обозначается точкой М( U ,V) , рис. 5.1. Множество точек М( U ,V) , отвечающих разным частотам, образуют кривую, которая называется годографом Михайлова.
Рассмотрим годографы Михайлова для устойчивых систем.
В случае устойчивых систем годограф Михайлова имеет свойство начинаться с точки U (0) = an , V (0) = 0. По мере увеличения w от нуля до бесконечности, точка М( U ,V) перемещается влево так, что кривая стремится охватить начало координат, одновременно удаляясь от него. Если провести радиус-вектор из начала координат в точку М( U ,V) , то окажется, что радиус-вектор будет поворачиваться против часовой стрелки, непрерывно увеличиваясь. Непрерывно увеличивается и угол, который он образует с осью абсцисс. Представив комплексное выражение в экспоненциальной форме,

обнаруживаем, что радиус-вектор есть модуль комплексного частотного полинома | D ( j w )| , а угол j ( w ) – аргумент. Модуль имеет величину 

Вид годографа Михайлова зависит от степени n характеристического полинома. Годографы полиномов первых четырех степеней показаны на рисунках далее. Они соответствуют устойчивым системам. Анализ годографов устойчивых систем позволяет сделать выводы, которые и составляют содержание критерия Михайлова.
Можно дать три формулировки критерию Михайлова.
Если при изменении частоты от нуля до бесконечности годограф Михайлова начинается на действительной оси в точке an , последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, не проходя через ноль, и уходит в бесконечность в n -м квадранте, — система устойчива.
Если при изменении частоты от нуля до бесконечности вектор комплексного частотного полинома D ( j w ) последовательно поворачивается против часовой стрелки на угол n ( p /2), где n – степень характеристического полинома, и нигде не становится нулем, — система устойчива.
Обратим внимание на частоты, при которых годограф пересекает оси координат. Назовем их «частоты пересечения». Первая частота нулевая, с нее начинается годограф. При w 1 = 0 U (0) = an , V (0) = 0 . Вторая отвечает точке пересечения годографом положительного отрезка оси ординат, U ( w 2) = 0 , V( w 2) – некоторое число. Непрерывно увеличивая частоту, при некоторой, равной w 3, получим пересечение годографа с отрицательной частью оси абсцисс. Очевидно, четвертым будет пересечение с отрицательной частью оси ординат при частоте w 4. Далее последуют частоты пересечения w 5, w 6, …, w n . Все они действительные положительные числа, каждое последующее больше предыдущего.
Третья формулировка критерия Михайлова
Если частоты пересечения годографа с осями координат чередуются и образуют возрастающую последовательность вида ω1 w n , — система устойчивая.
В отличие от предыдущих, третья формулировка позволяет исследовать устойчивость системы без построения годографа, аналитически. Соображения следующие.
Каждому пересечению годографом действительной оси (когда V ( w ) = 0) будет соответствовать корень нечетного полинома V ( w ). Каждому пересечению мнимой оси (когда U ( w ) = 0) будет соответствовать корень четного полинома U ( w ). Следовательно, по мере увеличения w корни полиномов V ( w ) и U ( w ) для устойчивой системы должны чередоваться (корень полинома V ( w ) сменяется корнем полинома U ( w ) и т.д.); корень каждого последующего пересечения оси должен быть больше предыдущего, все корни должны быть действительными. Общее число корней равно степени характеристического полинома.
В случае неустойчивых систем кривые не охватывают начало координат, чередования частот нечетного и четного полиномов нет.
Если годограф начинается из начала координат или проходит через начало координат, система находится на границе устойчивости.
http://mathhelpplanet.com/static.php?p=kriterii-ustoichivosti-gurvitsa-i-mihailova
http://mc-plc.ru/tau/kriteriy-ustoychivosti-mihaylova.htm