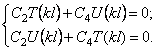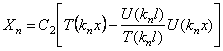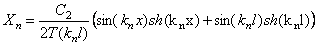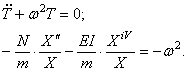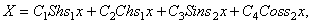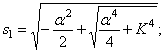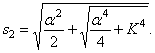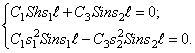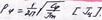Крутильные колебания вала уравнение движения

КРУТИЛЬНЫЕ КОЛЕБАНИЯ КОЛЕНЧАТОГО ВАЛА

Общие сведения

Крутильными колебаниями называются относительные угловые колебания сосредоточенных на валу масс, возникающие при неравномерном вращении вала под действием переменного крутящего момента.

Порядок расчета коленчатого вала на крутильные колебания следующий.

1. Приведение реальной динамической системы коленчатого вала к эквивалентной дискретной схеме:

а) определение моментов инерции сосредоточенных масс;

б) определение податливостей упругих соединений.

2. Расчет частот и амплитуд собственных крутильных колебаний вала.

3. Определение порядка главных и сильных гармоник крутящего момента.

4. Определение резонансных режимов работы.

5. Проведение гармонического анализа крутящего момента на резонансных режимах работы.

6. Определение амплитуд колебаний при резонансе.

7. Определение напряжений при резонансных колебаниях.

1. Приведение динамической системы двигателя сводится к определению моментов инерции элементов двигателя и податливостей отдельных участков вала. Реальные массы элементов коленчатого вала и другие движущиеся массы заменяют сосредоточенными в виде абсолютно жестких дисков нулевой толщины и соединяют их упругими элементами, обладающими только податливостями. Как правило, реальный двигатель разбивают по сечениям, расположенным по осям цилиндров и местам расположения шестерен, маховика и дополнительных агрегатов. На рисунке 5.1 представлены действительная динамическая система двухцилиндрового двигателя с распределительным валом механизма газораспределения с шестеренчатым приводом и приведенные эквивалентные крутильные системы.

Рис. 5.1. Схема приведения крутильной системы коленчатого вала

Кривошипно-шатунный механизм объединяют в одну массу, обладающую моментом инерции J_кшм

,

где J_кол – момент инерции колена вала;

J₂ – момент инерции нижней части шатуна, отнесенной к оси шатунной шейки;

J_пд – момент инерции поступательно движущихся масс.

.

.

Момент инерции колена

,

где J_кш – момент инерции коренных шеек;

J_щ – момент инерции щеки с противовесом;

J_шш – момент инерции шатунной шейки.

,

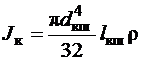
где r – плотность материала колена;

d_кш и l_кш – диаметр и длина коренной шейки.

,

где d_шш и l_шш – диаметр и длина шатунной шейки.

Момент инерции щеки, выполненной в виде параллелепипеда
(рис. 5.2)

.

Рис. 5.2. Щека простой формы Рис. 5.3. Щека сложной формы

Если форма щеки и противовесов отличается от параллелепипеда, то ее момент инерции находят методом разбиения на элементарные фигуры дугообразной формы, суммируя затем их моменты инерции (рис. 5.3)

,

.

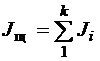
Податливость колена коленчатого вала

,

где l_пр – приведенная длина колена;

G – модуль упругости второго рода материала коленчатого вала.

Приведенная длина колена может определяться по эмпирической формуле:

где d_кш, d_кш.вн – внешний и внутренний диаметры коренной шейки соответственно;

d_ш d_ш.вн – внешний и внутренний диаметры и длина шейки соответственно;

h, b – толщина и ширина щеки соответственно.

Значения моментов инерции и податливостей системы после редуцирования (см. рисунок 5.1) определяются по следующим формулам

, , ,

где i_n = w₀/w – передаточное отношение передачи.

2. Частоты w_с и амплитуды а_i собственных крутильных колебаний вала для пятимассовой системы, показанной на рисунке 5.1 определяются из системы уравнений

.

Для крутильной системы из четырех и более масс система уравнений может решаться методом последовательных приближений. Количество корней системы уравнений равно количеству упругих соединений приведенной системы. Например, для пятимассовой системы, приведенной на рисунке 5.1, количество частот собственных колебаний w_с равно четырем.

Для двух- и трехмассовой систем система уравнений решается аналитически. Собственная частота для двухмассовой системы определяется по выражению

.

3. Расчет на крутильные колебания проводят для главных и сильных гармоник. Порядки главных гармоник равны или кратны числу рабочих ходов за один оборот коленчатого вала. Порядки сильных гармоник равны или кратны половине числа рабочих ходов за один оборот коленчатого вала.

4. Частоты собственных колебаний, при которых возникает резонанс, лежат в интервале

где n_min, n_max– минимальный и максимальный порядки моторных гармоник;

w_min, w_max – минимальная и максимальная частоты вращения коленчатого вала.

Для четырехтактного двигателя n_min = 0,5, для двухтактного двигателя n_min = 1. При числе цилиндров двигателя четыре или меньше ограничиваются максимальным порядком гармоники n_max = 6, при числе цилиндров больше четырех – n_max = 10.

Резонансная частота n-й гармоники (частота вращения коленчатого вала, на которой возникает резонанс)

.

5. Гармонический анализ крутящего момента двигателя проводится на резонансных частотах. В результате анализа определяется амплитуда гармонической составляющей крутящего момента n-й гармоники. Гармонический анализ может проводиться численно на ЭВМ.

6. Амплитуда вынужденных колебаний первой массы при резонансе

,

где – амплитуда гармонической составляющей крутящего момента, полученная из гармонического анализа;

– равнодействующий вектор амплитуд перемещений;

b = b_уF_пR 2 i_ц– коэффициент демпфирования при внешнем трении (b_у – удельный коэффициент демпфирования, F_п – площадь поршня, R – радиус кривошипа, i_ц – число цилиндров);

y – коэффициент поглощения внутреннего трения (0,01-02 – для стали, 0,2-0,3 – для чугуна);

n – порядок гармонической составляющей крутящего момента, на которой рассчитывается резонанс;

a_i – амплитуда собственных крутильных колебаний i-ой массы крутильной системы, на которые действует возмущающий момент.

Значения удельного коэффициента демпфирования b_у [Н×с/м 3 ] можно принять следующими:

Равнодействующий вектор амплитуд перемещений находят при помощи фазовых диаграмм. Для этого из центра диаграммы откладывают вверх вектор амплитуды первой массы гармоники n-го порядка. Векторы амплитуд остальных масс откладывают из того же центра согласно порядку работы двигателя под углами nd_i к первому вектору и затем находят сумму векторов (d_i – угол поворота коленчатого вала между вспышками в первом и i-ом цилиндре). На рисун-
ке 5.4 представлен пример построения фазовой диаграммы шестицилиндрового рядного двигателя с порядком работы цилиндров 1-5-3-6-2-4.

Рис. 5.4. Фазовая диаграмма шестицилиндрового двигателя

Амплитуда вынужденных колебаний других массы при резонансе

7. Касательные напряжения в элементах крутильной системы при резонансе

,

где U – эластический момент на участке вала между i-ой и i–1-ой массами;

– полярный момент сопротивления сечения вала (d_н и d_вн – наружный и внутренний диаметры вала).

Допускаемые напряжения для колена вала [t] = 30-45 МПа; для гладкого вала [t] = 50-60 МПа.

Задачи

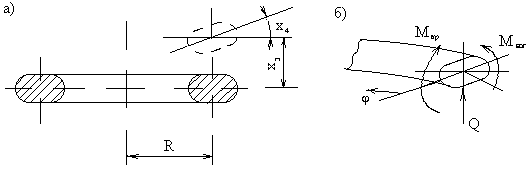
Задача 5.1. Привести реальную крутильную систему коленчатого вала (рис. 5.5) к динамически эквивалентной дискретной. Масса поступательно движущихся частей КШМ 0,9 кг, масса шатуна
0,8 кг. Радиус кривошипа 70 мм, диаметр коренных шеек 60 мм, длина коренных шеек 30 мм, диаметр шатунной шейки 56 мм, длина шатунной шейки 35 мм, ширина щеки 70 мм, толщина щеки 20 мм. Диаметры шестерен: d₁ = 120 мм, d₂ = 80 мм; ширина шестерен 20 мм. Диаметр маховика d_м = 300 мм и его ширина 30 мм. При расчете момента инерции шестерен и маховика считать их сплошными дисками.

Рис. 5.5. К задаче 5.1

Задача 5.2. Определить частоты и амплитуды свободных колебаний четырехмассовой крутильной системы, представленной на рисунке 5.6. Моменты инерции элементов крутильной системы: J₁ =
= 0,05 кг×м 2 ; J₂ = 0,04 кг×м 2 ; J₄ = 0,8 кг×м 2 . Податливости упругих соединений системы: e_1,2 = e_2,3 = 14×10 -8 1/Н×м.

Рис. 5.6. К задаче 5.2

Задача 5.3. Определить порядки главных и сильных гармоник крутящего момента трехцилиндрового четырехтактного двигателя, двухцилиндрового двухтактного двигателя и четырехцилиндрового четырехтактного двигателя.

Задача 5.4. Определить резонансные режимы работы четырехцилиндрового четырехтактного двигателя, если скоростной диапазон работы двигателя от 800 до 5 800 об/мин. Частоты свободных крутильных колебаний коленчатого вала: 3 000, 7 000, 16 000 и
24 000 рад/с.

Задача 5.5. Определить амплитуды вынужденных колебаний в коленчатом валу четырехцилиндрового двигателя при резонансных крутильных колебаниях от гармонической составляющей 2-го порядка крутящего момента, амплитуда которой равна 70 Н×м, при частоте вращения вала двигателя 6 000 об/мин. Диаметр поршня 90 мм, ход поршня 88 мм. Амплитуды свободных колебаний масс коленчатого вала при частоте вращения 12 000 об/мин: а₁ = 1; а₂ = 0,7; а₃ = 0,3;
а₄ = -0,1; а₅ = -0,2. Податливости всех упругих соединений принять равными 2×10 -7 1/Н×м.

Задача 5.6. Определить напряжения кручения в задней коренной шейке коленчатого вала двигателя, представленного на рисунке 5.5 при резонансных крутильных колебаниях, если амплитуда колебаний моторной массы равна 0,04 рад, амплитуда колебаний маховика равна -0,01 рад.

6. КИНЕМАТИКА И ДИНАМИКА МЕХАНИЗМА
ГАЗОРАСПРЕДЕЛЕНИЯ

Общие сведения

Кинематика деталей ГРМ зависит от профиля кулачка и схемы механизма ГРМ.

На рисунке 6.1 показана схема толкателя с выпуклым кулачком, образованным тремя дугами окружностей двух радиусов. Законы изменения перемещения, скорости и ускорения толкателя будут состоять из двух участков.

Рис. 6.1. Схема толкателя с выпуклым кулачком ГРМ

Перемещения, скорости и ускорения толкателя при частоте вращения распредвала w_р для выпуклого кулачка на участке I (по радиусу R) в зависимости от угол поворота распредвала a_р

;

на участке II (по радиусу r)

,

где .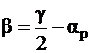

Зависимости перемещения, скорости и ускорения толкателя от угла поворота распредвала представлены на рисунке 6.2.

Рис. 6.2. Зависимости перемещения, скорости и ускорения толкателя
ГРМ с выпуклым кулачком

Безударные кулачки, построенные по методу «полидайн», обеспечивают движение толкателя по закону

,

где a_р – угол поворота, отсчитываемый от вершины кулачка;

С – постоянные коэффициенты;

g – угол профиля кулачка от h = 0 до h = h_max;

p, q, r, s – постоянные числа, подчиняющиеся закону арифметической прогрессии (p = 6-14, q = 10-26, r = 14-38, s = 18-50).

Коэффициенты С определяются по уравнениям

При совпадении частоты вынуждающих сил m_в с собственной частотой колебаний клапанных пружин возникают резонансные колебания.

Собственная частота колебаний пружины

,

где r – плотность материала пружины;

G – модуль упругости второго рода материала пружины;

n_рв = n₀ – 2 – число рабочих витков пружины;

n₀ – общее количество витков;

D – средний диаметр пружины;

d – диаметр проволоки.

При проектировании пружин стараются выполнить условие
m_с > 10m_в.

При расчете динамики клапанного механизма учитывают силы давления газов, силы инерции движущихся деталей, силы сжатия клапанных пружин. Все силы приводятся к оси клапана или оси толкателя.

Газовая сила, действующая на выпускной клапан

,

где p_ц – давление газа в цилиндре двигателя;

p_вып – давление газа в выпускном трубопроводе за клапаном;

d – диаметр клапана;

Газовая сила, действующая на впускной клапан

,

где p_вп – давление газа во впускном трубопроводе перед клапаном.

Силы инерции движущихся деталей ГРМ

,

где m_S – приведенная масса всех движущихся деталей ГРМ;

j – ускорение клапана или толкателя.

Сила сжатия цилиндрической клапанной пружины

,

где f – прогиб пружины.

Вертикальная составляющая силы давления кулачка на толкатель

.

Боковое давление на втулку толкателя (горизонтальная составляющая)

где m – коэффициент трения.

Приведенные к оси толкателя газовая сила и сила сжатия пружины для схемы ГРМ, представленной на рисунке 6.3

.

Приведенные к оси толкателя массы клапана и пружины при угле между осью толкателя и коромыслом, а также между осью клапана и коромыслом »90°

,

где m_кл и m_пр – массы клапана и пружины.

Приведенная масса коромысла

,

где J_кор – момент инерции коромысла относительно оси вращения.

Масса всех движущихся деталей, приведенная к оси толкателя

,

где m_тш – суммарная масса толкателя и штанги.

Задачи

Задача 6.1. Увеличить собственную частоту колебаний пружины ГРМ в два раза, сохранив величину предварительного усилия, предварительного прогиба, равного 10 мм и максимального хода толкателя, равного 9 мм. Средний диаметр пружины 30 мм, диаметр проволоки 3,5 мм, количество рабочих витков 9, плотность материала пружины 7800 кг/м 3 , модуль упругости второго рода материала пружины 0,8×10 5 МПа.

Задача 6.2. Определить максимальную нагрузку на толкатель ГРМ (рис. 6.3) с выпуклым кулачком, схема которого представлена на рисунке 6.1 при частоте вращения распределительного вала 300 рад/с. Размеры кулачка: R = 0,065 м; r_н= 0,02 м; r = 0,003 м; а = 0,03 м;
g= 140° (см. рисунок 6.1). Размеры пружины: диаметр пружины
40 мм, диаметр проволоки 4 мм, количество рабочих витков 8, высота пружины в свободном состоянии 70 мм, предварительное сжатие пружины 30 мм. Масса клапана 80 г, масса штанги 100 г, масса толкателя 50 г, момент инерции коромысла 0,0003 кг×м 2 .

Рис. 6.3. К задаче 6.2

Задача 6.3. Определить, не произойдет ли разрыв кинематической связи в ГРМ по условиям задачи 6.2.

Задача 6.4. Определить максимальную нагрузку на толкатель ГРМ (рис. 6.4) с выпуклым кулачком, схема которого представлена на рисунке 6.1, при частоте вращения распределительного вала
300 рад/с. Размеры кулачка: R = 0,065 м; r_н= 0,02 м; r = 0,003 м;
а = 0,03 м; g= 140°. Размеры пружины: диаметр пружины 40 мм, диаметр проволоки 4 мм, количество рабочих витков 8, высота пружины в свободном состоянии 70 мм, предварительное сжатие пружины
30 мм. Масса клапана 80 г, масса толкателя 50 г.

Рис. 6.4. К задаче 6.4

Задача 6.5. Определить максимальное ускорение толкателя при двух профилях кулачка: выпуклом и безударном («полидайн») при частоте вращения распределительного вала 400 1/с. Размеры выпуклого кулачка: R = 0,07 м; r_н= 0,025 м; r = 0,006 м; а = 0,033 м;
g= 140°. Параметры кулачка «полидайн»: угол профиля g= 140°, максимальный подъем толкателя h_max = 14 мм, постоянные числа для расчета кулачка p = 6, q = 10, r = 14, s = 18.

Задача 6.6. Сравнить время-сечение клапанов, открываемых выпуклым кулачком и безударным кулачком по условиям задачи 6.5.

СПИСОК ЛИТЕРАТУРЫ

1. Луканин, В. Н. Двигатели внутреннего сгорания: учебник для вузов в 3 т. Т.2: Динамика и конструирование / В. Н. Луканин [и др.]; под ред. В. Н. Луканина, М. Г. Шатрова. – Изд. 4-е, перераб. и доп. – М.: Высшая школа, 2009 – 400 с.

2. Яманин, А.И. Динамика поршневых двигателей: Учебное пособие /Яманин А.И., Жаров А.В. – М.: Машиностроение, 2003. – 464 с.

3. Чистяков, В. К. Динамика поршневых и комбинированных двигателей внутреннего сгорания: Учеб. пособие для машиностроительных вузов по специальности «Двигатели внутреннего сгорания». – М.: Машиностроение, 1989. – 256 с.

4. Дьяченко, Н.Х. Конструирование и расчет двигателей внутреннего сгорания: Учебник для вузов / Н.Х. Дьяченко, Б.А. Харитонов, В.М. Петров и др.; Под ред. Дьяченко Н.Х. – Л.: Машиностроение, 1979. – 392 с.

Составитель ВАХИТОВ Юрий Рашитович

по дисциплине «Динамика двигателей»

Подписано в печать __.__._______. Формат 60×84 1/16.

Бумага офсетная. Печать плоская. Гарнитура Times New Roman.
Усл. печ. л. 1,9. Уч.-изд. л. 1,8.

Тираж 50 экз. Заказ № ______

ФГБОУ ВПО «Уфимский государственный авиационный

Редакционно-издательский комплекс УГАТУ

450000, Уфа-центр, ул. К. Маркса, 12

Раздел 6. Свободные колебания систем с распределёнными параметрами

Основная особенность процесса свободных колебаний систем с бесконечным числом степеней свободы выражается в бесконечности числа собственных частот и форм колебаний. С этим связаны и особенности математического характера: вместо обыкновенных дифференциальных уравнений, описывающих колебания систем с конечным числом степеней свободы, здесь приходится иметь дело с дифференциальными уравнениями в частных производных. Кроме начальных условий, определяющих начальные смещения и скорости, необходимо учитывать и граничные условия, характеризующие закрепление системы.

6.1. Продольные колебания стержней

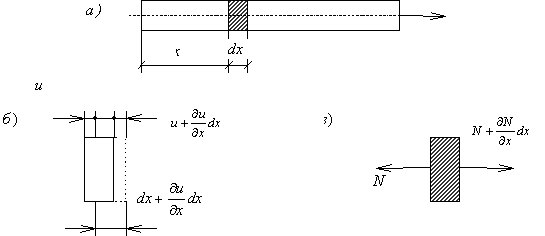
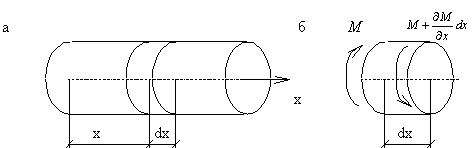
При анализе продольных колебаний прямолинейного стержня (рис.67,а) будем считать, что поперечные сечения остаются плоскими и что частицы стержня не совершают поперечных движений, а перемещаются только в продольном направлении.

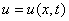
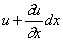
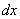
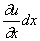
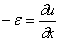
Пусть u — продольное перемещение текущего сечения стержня при колебаниях; это перемещение зависит от расположения сечения (координаты x ) и от времени t . Таким образом, есть функция двух переменных; её определение и представляет основную задачу. Перемещение бесконечно близкого сечения равно , следовательно, абсолютное удлинение бесконечно малого элемента равно (рис.67,б), а относительное его удлинение .

Соответственно продольная сила в сечении с координатой х может быть записана в виде

, (173)

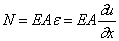
где жёсткость стержня при растяжении (сжатии). Сила N также является функцией двух аргументов – координаты х и времени t .

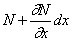
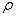
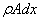
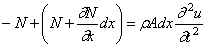
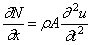
Рассмотрим элемент стержня, расположенный между двумя бесконечно близкими сечениями (рис.67,в). К левой грани элемента приложена сила N, а к правой – сила . Если обозначить через плотность материала стержня, то масса рассматриваемого элемента составляет . Поэтому уравнение движения в проекции на ось х

,

. (174)

Учитывая (173) и принимая A = const , получим

, (175)

. (176)

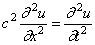
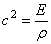
Следуя методу Фурье, ищем частное решение дифференциального уравнения (175) в виде

, (177)

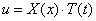
т.е. предположим, что перемещение u можно представить в виде произведения двух функций, одна из которых зависит только от аргумента х , а другая только от аргумента t . Тогда вместо определения функции двух переменных u ( x , t ) необходимо определять две функции X( x ) и T( t ), каждая из которых зависит только от одной переменной.

Подставив (177) в (174), получим

,

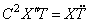
где штрихами обозначена операция дифференцирования по x , а точками – по t . Перепишем это уравнение таким образом:

.

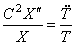
Здесь левая часть зависит только от x,а правая – только от t . Для тождественного выполнения этого равенства (при любых x и t ) необходимо, чтобы каждая из его частей была равна постоянной, которую обозначим через :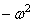

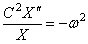
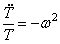
; . (178)

Отсюда следуют два уравнения:

; . (179)

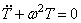
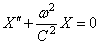
Первое уравнение имеет решение:

, (180)

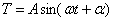
указывающее на колебательный характер, причём из (180) видно, что неизвестная величина имеет смысл частоты свободных колебаний.

Второе из уравнений (179) имеет решение:

, (181)

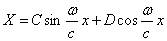
определяющее форму колебаний.

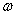
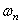
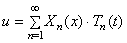
Частотное уравнение, определяющее величину , составляется путём использования граничных условий. Это уравнение всегда трансцендентное и имеет бесконечное число корней. Таким образом, число собственных частот бесконечно, причём каждому значению частоты соответствует своя функция T_n ( t ), определяемая зависимостью (180), и своя функция Xn ( x ), определяемая зависимостью (181). Решение (177) является лишь частным и не даёт полного описания движения. Полное решение получается путём наложения всех частных решений:

.

Функции X_n ( x ) называются собственными функциями задачи и описывают собственные формы колебаний. Они не зависят от начальных условий и удовлетворяют условию ортогональности, которое при А=const имеет вид

, если .

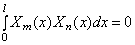
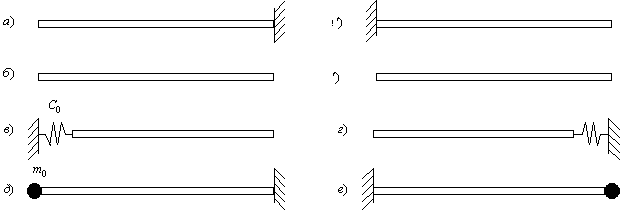
Рассмотрим некоторые варианты граничных условий.

Закреплённый конец стержня (рис.68,а). В концевом сечении перемещение u должно быть равно нулю; отсюда следует, что в этом сечении

Свободный конец стержня (рис.68,б). В концевом сечении продольная сила

(183)

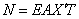
должна тождественно равняться нулю, что возможно, если в концевом сечении X’=0.

Упругозакреплённый конец стержня (рис.68,в).

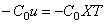
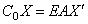
При перемещении u концевого стержня возникает упругая реакция опоры , где С_о — жёсткость опоры. Учитывая (183) для продольной силы, получим граничное условие

,

если опора расположена на левом конце стержня (рис.68,в), и

,

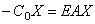
если опора расположена на правом конце стержня (рис.68,г).

Сосредоточенная масса 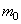на конце стержня.

Развиваемая массой сила инерции:

.

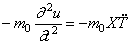
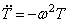
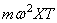
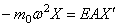
Так как, согласно первому из уравнений (179), , то сила инерции может быть записана в виде . Получаем граничное условие

,

если масса находится на левом конце (рис.68,д), и

, (184)

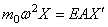
если масса связана с правым концом (рис.68,е).

Определим собственные частоты консольного стержня (рис.68,a’).

Согласно (182) и (183), граничные условия

X’=0 при х= .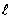

Подставляя поочерёдно эти условия в решение (181), получим

D=0; .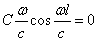

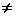
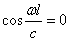
Условие С 0 приводит к частотному уравнению:

.

Корни этого уравнения

(n=1,2,…)

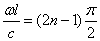
определяют собственные частоты:

(n=1,2,…). (185)

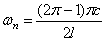
Первая (низшая) частота при n=1:

.

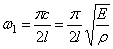
Вторая частота (при n=2):

и т. д.

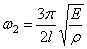
Определим собственные частоты стержня с массой 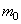на конце (рис.68,е).

Согласно (182) и (184), имеем

при х= .

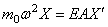
Подставляя эти условия в решение (181), получим:

D=0; .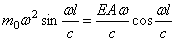

Следовательно, частотное уравнение при учёте (176) имеет вид

.

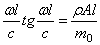
Здесь правая часть представляет собой отношение массы стержня к массе концевого груза.

Для решения полученного трансцендентного уравнения необходимо воспользоваться каким-либо приближённым способом.

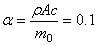
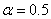
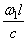
При и значения наиболее важного низшего корня будут соответственно 0.32 и 0.65 .

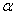
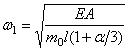
При малом отношении решающее влияние оказывает груз и хорошие результаты даёт приближённое решение

.

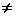
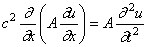
Для стержней переменного сечения, т.е. при А const , из (173) и (174) получается уравнение движения в виде

.

Это дифференциальное уравнение не поддаётся решению в замкнутом виде. Поэтому в подобных случаях приходится прибегать к приближённым методам определения собственных частот.

6.2. Крутильные колебания валов

Крутильные колебания вала с непрерывно распределенной массой (рис.69,а) описываются уравнениями, которые по структуре полностью совпадают с приведенными выше уравнениями продольных колебаний стержней.

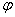
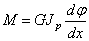
Крутящий момент М в сечении с абсциссой х связан с углом поворота дифференциальной зависимостью, аналогичной (173):

, (186)

где J_p-полярный момент инерции поперечного сечения.

В сечении, расположенном на расстоянии dx , крутящий момент равен (рис.69,б):

.

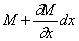
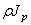
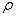
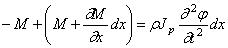
Обозначая через (где — плотность материала вала) интенсивность момента инерции массы вала относительно его оси (т.е. момент инерции единицы длины), уравнение движения элементарного участка вала можно записать так:

,

или подобно (174):

.

Подставляя сюда выражение (186), при Jp=const получим, аналогично (175):

, (187)

.

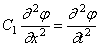
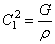
Общее решение уравнения (187), как и уравнения (175), имеет вид

,

(188)

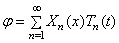
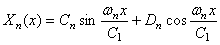
Собственные частоты и собственные функции при этом определяются конкретными граничными условиями.

В основных случаях закрепления концов аналогично случаю продольных колебаний получим

а) закрепленный конец ( 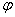=0): Х=0;

б) свободный конец (М=0): Х’=0;

в) упругозакрепленный левый конец: СоХ=GJpX ‘ ( Со-коэффициент жёсткости);

г) упругозакрепленный правый конец: — СоХ=GJpX ‘;

д ) диск на левом конце: 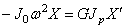(Jo-момент инерции диска относительно оси стержня);

е) диск на правом конце: .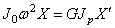

Если вал закреплён на левом конце (х=0), а правый конец ( х= ) свободен, то Х=0 при х=0 и Х’=0 при x= ; собственные частоты определяются аналогично (185):

(n=1,2,…).

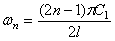
Если левый конец закреплён, а на правом конце имеется диск, получим трансцендентное уравнение:

.

Если оба конца вала закреплены, то граничные условия будут X=0 при х=0 и х= . В этом случае из (188) получим

; D=0,

(n=1,2,…),

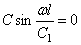
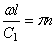
отсюда находим собственные частоты:

.

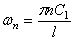
Если левый конец вала свободен, а на правом конце имеется диск, то X’=0 при х=0 ; Jo 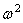X=GJpX ‘ при х= .

При помощи (188) находим

С=0; ,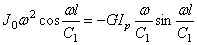

или трансцендентное частотное уравнение:

.

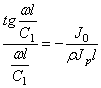
6.3.Изгибные колебания балок

6.3.1.Основное уравнение

Из курса сопротивления материалов известны дифференциальные зависимости при изгибе балок:

; (189)

, (190)

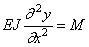
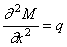
где EJ — жёсткость при изгибе; y=y ( x , t ) — прогиб; M=M( x , t ) — изгибающий момент; q — интенсивность распределённой нагрузки.

Объединяя (189) и (190), получим

. (191)

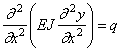
В задаче о свободных колебаниях нагрузкой для упругого скелета являются распределённые силы инерции:

,

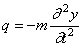
где m — интенсивность массы балки (масса единицы длины), и уравнение (191) принимает вид

.

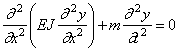
В частном случае постоянного поперечного сечения, когда EJ = const , m = const , имеем:

. (192)

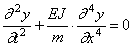
Для решения уравнения (192) полагаем, как и выше,

y = X ( x ) × T ( t ). (193)

Подставляя (193) в (192), приходим к уравнению:

.

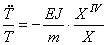
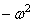
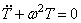
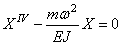
Для тождественного выполнения этого равенства необходимо, чтобы каждая из частей равенства была постоянной. Обозначая эту постоянную через , получим два уравнения:

; (194)

. (195)

Первое уравнение указывает на то, что движение носит колебательный характер с частотой .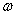

Второе уравнение определяет форму колебаний. Решение уравнения (195) содержит четыре постоянных и имеет вид

,

. (196)

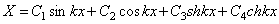
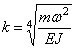
Удобно использовать вариант записи общего решения, предложенный А.Н.Крыловым:

, (197)

(198)

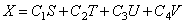
представляют собой функции А.Н.Крылова.

Обратим внимание на то, что S=1, T=U=V=0 при x=0. Функции S,T,U,V связаны между собой следующим образом:

(199)

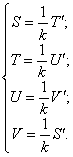
Поэтому производные выражения (197) записываются в виде

(200)

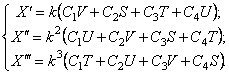
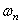
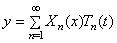
В задачах рассматриваемого класса число собственных частот бесконечно велико; каждой из них отвечает своя функция времени T_n и своя фундаментальная функция X_n . Общее решение получится путём наложения частных решений вида (193)

. (201)

Для определения собственных частот и формул необходимо рассмотреть граничные условия.

6.3.2. Граничные условия

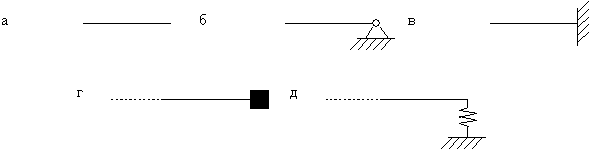
Для каждого конца стержня можно указать два граничных условия .

Свободный конец стержня (рис. 70,а). Нулю равны поперечная сила Q=EJX»’T и изгибающий момент M=EJX»T. Поэтому граничные условия имеют вид

Шарнирно-опёртый конец стержня (рис.70,б). Нулю равны прогиб y=XT и изгибающий момент M=EJX»T. Следовательно, граничные условия таковы:

Защемленный конец (рис.70,в). Нулю равны прогиб y=XT и угол поворота . Граничные условия:

На конце стержня имеется точечный груз массы (рис.70,г). Его сила инерции может быть при помощи уравнения (194) записана так: ; она должна быть равна поперечной силе Q=EJX»’T , поэтому граничные условия принимают вид

; X»=0 . (205)

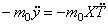
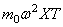
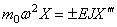
В первом условии знак плюс принимается в случае, когда точечный груз связан с левым концом стержня, и знак минус, когда он связан с правым концом стержня. Второе условие вытекает из отсутствия изгибающего момента .

Упруго-опертый конец стержня (рис.70,д). Здесь изгибающий момент равен нулю, а поперечная сила Q=EJX»’T равна реакции опоры 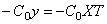(C_o-коэффициент жёсткости опоры).

X»=0 ; 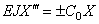(206)

(знак минус принимается в случае, когда упругая опора является левой, и знак плюс, когда она является правой).

6.3.3. Частотное уравнение и собственные формы

Развёрнутая запись граничных условий приводит к однородным уравнениям относительно постоянных C₁, C₂, C₃, C₄.

Чтобы эти постоянные не равнялись нулю, должен равняться нулю определитель, составленный из коэффициентов системы; это приводит к частотному уравнению. При этих операциях выясняются соотношения между C₁, C₂, C₃, C₄, т.е. определяются собственные формы колебаний (с точностью до постоянного множителя).

Проследим составление частотных уравнений на примерах.

Для балки с шарнирно-опёртыми концами согласно (203) имеем следующие граничные условия: X=0; X»=0 при x=0 и x= . При помощи (197)-(200) получим из первых двух условий: C₁=C₃=0. Два оставшихся условия можно записать в виде

Чтобы C₂ и C₄ не были равны нулю, необходимо равенство нулю определителя:

.

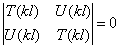
Таким образом, частотное уравнение имеет вид

.

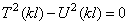
Подставляя выражения T и U, получим

.

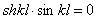
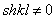
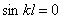
Так как , то окончательно частотное уравнение записывается так:

. (207)

Корни этого уравнения:

, ( n =1,2,3. ).

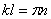
Учитывая (196), получим

. (208)

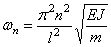
Перейдём к определению собственных форм. Из записанных выше однородных уравнений вытекает следующее соотношение между постоянными C₂ и C₄:

.

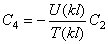
Следовательно, (197) приобретает вид

Согласно (207), имеем

, (209)

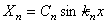
где 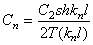— новая постоянная, значение которой остаётся неопределённым, пока не введены в рассмотрение начальные условия.

6.3.4. Определение движения по начальным условиям

Если требуется определить движение, следующее после начального возмущения, то необходимо указать для всех точек балки как начальные смещения, так и начальные скорости:

(210)

и использовать свойство ортогональности собственных форм:

.

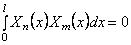
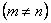
Общее решение (201) запишем так:

. (211)

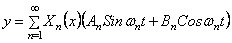
Скорость определяется выражением

. (212)

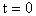
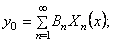
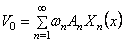
Подставляя в правые части уравнений (211) и (212) , а в левые части — предполагаемые известными начальные смещения и скорости, получим

.

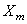
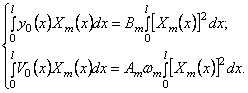
Умножая эти выражения на и интегрируя по всей длине, имеем

(213)

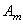
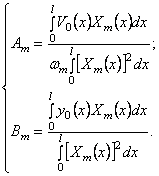
Бесконечные суммы в правых частях исчезли вследствие свойства ортогональности. Из (213) следуют формулы для постоянных и

(214)

Теперь эти результаты нужно подставить в решение (211).

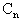
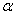
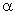
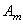
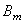
Снова подчеркнём, что выбор масштаба собственных форм несущественен. Если, например, в выражении собственной формы (209) принять вместо величину в раз большую, то (214) дадут результаты в раз меньшие; после подстановки в решение (211) эти различия компенсируют друг друга. Тем не менее часто пользуются нормированными собственными функциями, выбирая их масштаб таким, чтобы знаменатели выражений (214) равнялись единице, что упрощает выражения и .

6.3.5. Влияние постоянной продольной силы

Рассмотрим случай, когда колеблющаяся балка испытывает действие продольной силы N , величина которой не меняется в процессе колебаний. В этом случае уравнение статического изгиба усложняется и приобретает вид (при условии, что сжимающая сила считается положительной)

.

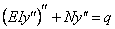
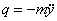
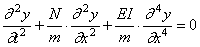
Полагая и считая жёсткость постоянной, получаем уравнение свободных колебаний

. (215)

Принимаем по-прежнему частное решение в виде .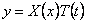

Тогда уравнение (215) распадается на два уравнения:

Первое уравнение выражает колебательный характер решения, второе определяет форму колебаний, а также позволяет найти частоты. Перепишем его таким образом:

(216)

где K определяется формулой (196), а

. (217)

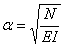
Решение уравнения (216) имеет вид

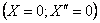
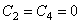
Рассмотрим случай, когда оба конца стержня имеют шарнирные опоры. Условия на левом конце дают . Удовлетворяя те же условия на правом конце, получим

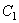
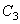
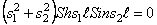
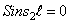
Приравнивая нулю определитель, составленный из коэффициентов при величинах и , приходим к уравнению

,

. (218)

Корни этого частотного уравнения:

.

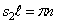
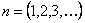
Следовательно, собственная частота определится из уравнения

.

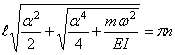
Отсюда при учёте (217) находим

. (219)

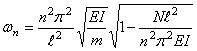
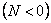
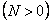
При растяжении частота увеличивается, при сжатии уменьшается. Когда сжимающая сила N приближается к критическому значению, корень стремится к нулю.

6.3.6. Влияние цепных усилий

Ранее продольная сила считалась заданной и не зависящей от перемещений системы. В некоторых практических задачах сопровождающая процесс поперечных колебаний продольная сила возникает вследствие изгиба балки и носит характер реакции опоры. Рассмотрим, например, балку на двух шарнирно-неподвижных опорах. При её изгибе возникают горизонтальные реакции опор, вызывающие растяжение балки; соответствующее горизонтальное усилие принято называть цепным усилием. Если балка совершает поперечные колебания, то цепное усилие будет изменяться во времени.

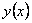
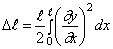
Если в мгновение t прогибы балки определяются функцией , то удлинение оси можно найти по формуле

.

Соответствующее цепное усилие найдём при помощи закона Гука

.

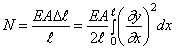
Подставим этот результат в (215) вместо продольной силы N (с учётом знака)

. (220)

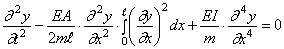
Полученное нелинейное интегродифференциальное уравнение упрощается при помощи подстановки

, (221)

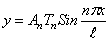
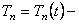
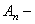
где безразмерная функция времени, максимальное значение которой можно положить равным любому числу, например, единице; амплитуда колебаний.

Подставляя (221) в (220), получим обыкновенное дифференциальное уравнение

, (222)

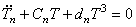
коэффициенты которого имеют следующие значения:

; .

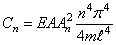
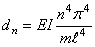
Дифференциальное уравнение (222) является нелинейным, следовательно, частота свободных колебаний зависит от их амплитуды.

Точное решение для частоты поперечных колебаний имеет вид

,

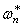
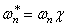
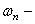
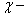
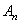
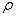
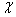
где частота поперечных колебаний, вычисленная без учёта цепных усилий; поправочный коэффициент, зависящий от отношения амплитуды колебаний к радиусу инерции поперечного сечения ; величина приводится в справочной литературе.

При соизмеримости амплитуды и радиуса инерции поперечного сечения поправка к частоте становится значительной. Если, например, амплитуда колебаний стержня круглого сечения равна его диаметру, то 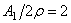, и частота почти в два раза больше, чем в случае свободного смещения опор.

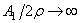
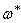
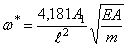
Случай соответствует нулевому значению радиуса инерции, когда изгибная жёсткость балки исчезающе мала — струна. При этом формула для даёт неопределённость. Раскрывая эту неопределённость, получим формулу для частоты колебаний струны

.

Эта формула относится к случаю, когда в положении равновесия натяжение равно нулю. Часто задачу о колебаниях струны ставят в других предположениях: считают, что перемещения малы, а растягивающая сила задана и остаётся неизменной в процессе колебаний.

При этом формула для частоты имеет вид

,

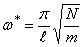
где N — постоянная растягивающая сила.

6.4. Влияние вязкого трения

Ранее предполагалось, что материал стержней идеально упругий и трение отсутствует. Рассмотрим влияние внутреннего трения, считая, что оно является вязким; тогда связь напряжений с деформациями описывается соотношениями

; . (223)

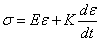
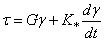
Пусть стержень с распределёнными параметрами совершает свободные продольные колебания. В этом случае продольная сила запишется в виде

. (224)

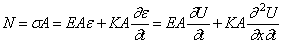
Из уравнения движения элемента стержня было получено соотношение (174)

.

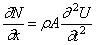
Подставляя сюда (224), приходим к основному дифференциальному уравнению

, (225)

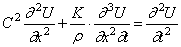
которое отличается от (175) вторым слагаемым, выражающим влияние сил вязкого трения.

Следуя методу Фурье, ищем решение уравнения (225) в виде

, (226)

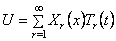
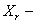
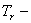
где функция только координаты x , а функция только времени t .

При этом каждый член ряда должен удовлетворять граничным условиям задачи, а вся сумма — также и начальным условиям. Подставляя (226) в (225) и требуя, чтобы равенство удовлетворялось для любого номера r , получим

, (227)

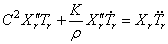
где штрихи обозначают дифференцирование по координате x , а точки — дифференцирование по времени t .

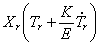
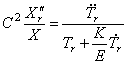
Разделив (227) на произведение , приходим к равенству

, (228)

левая часть, которого может зависеть только от координаты x , а правая — только от времени t . Для тождественного выполнения равенства (228) необходимо, чтобы обе части были равны одной и той же постоянной, которую обозначим через .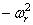

Из этого следуют уравнения

(229)

. (230)

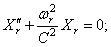
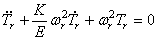
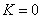
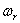
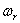
Уравнение (229) не зависит от коэффициента вязкости K и, в частности, остаётся таким же в случае идеально упругой системы, когда . Поэтому числа полностью совпадают с найденными ранее; однако, как будет показано ниже, величина даёт лишь приближённое значение собственной частоты. Отметим, что собственные формы совершенно не зависят от вязких свойств стержня, т.е. формы свободных затухающих колебаний совпадают с формами свободных незатухающих колебаний.

Теперь перейдём к уравнению (230), описывающему процесс затухающих колебаний; его решение имеет вид

, (231)

; (232)

. (233)

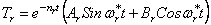
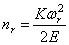
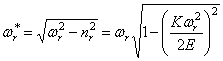
Выражение (232) определяет темп затухания, а (233) — частоту колебаний.

Таким образом, полное решение уравнения задачи

. (234)

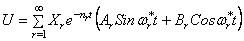
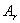
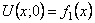
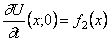
Постоянные и всегда можно найти по заданным начальным условиям. Пусть начальные смещения и начальные скорости всех сечений стержня заданы следующим образом:

; , (235)

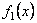
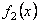
где и — известные функции.

Тогда при 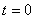, согласно (211) и (212), имеем

умножая обе части этих равенств на 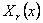и интегрируя в пределах всей длины стержня, получим

(236)

Соответственно условию ортогональности собственных форм все остальные слагаемые, входящие в правые части этих равенств, обращаются в нуль. Теперь из равенств (236) легко найти 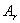и для любого номера r .

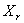
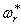
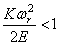
Рассматривая (232) и (234), заметим, что чем выше номер формы колебаний , тем быстрее её затухание. Кроме того, слагаемые, входящие в (234), описывают затухающие колебания, если есть действительное число. Из (233) видно, что это имеет место лишь для нескольких начальных значений r , пока выполняется неравенство

. (237)

При достаточно больших значениях r неравенство (237) нарушается и величина 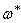становится мнимой. При этом соответствующие члены общего решения (234) уже не будут описывать затухающие колебания, но будут представлять апериодическое затухающее движение. Другими словами, колебания, в обычном смысле слова, выражает только некоторая конечная часть суммы (234).

Все эти качественные выводы относятся не только к случаю продольных колебаний, но и к случаям крутильных и изгибных колебаний.

6.5. Колебания стержней переменного сечения

В тех случаях, когда распределённая масса и сечение стержня переменны по его длине, следует вместо уравнения продольных колебаний (175) исходить из уравнения

. (238)

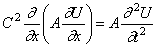
Уравнение крутильных колебаний (187) должно быть заменено уравнением

, (239)

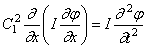
а уравнение поперечных колебаний (192) – уравнением

. (240)

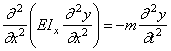
Уравнения (238)-(240) при помощи однотипных подстановок ; ; можно привести к обыкновенным дифференциальным уравнениям для функции

(241)

(242)

(243)

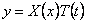
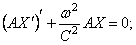
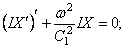
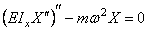
и одному однотипному уравнению для функции .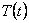

Уравнения (241)-(243) в отличие от уравнений, решённых выше, имеют переменные коэффициенты.

Замкнутую форму решений можно получить лишь в отдельных случаях, когда переменные 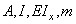определены специальными зависимостями. В общем случае неизбежен переход к приближённым методам. В частности, возможен путь, основанный на сосредоточении распределённой массы в ряде точек по длине стержня, после чего система сохраняет лишь конечное число степеней свободы, равное числу точек приведения. Используются также различные варианты вариационного метода и некоторые другие приближённые методы, о которых речь пойдёт ниже.

6.6. Колебания круговых колец

6.6.1. Колебания в плоскости кольца

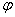
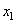
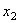
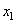
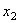
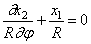
Рассмотрим круговой брус малой кривизны постоянного сечения с радиусом R осевой линии (рис.71,а). Будем считать груз нерастяжимым. Перемещение центра тяжести поперечного сечения, зафиксированного угловой координатой , можно разложить на радиальный и окружной компоненты — соответственно и . Из условия нерастяжимости оси бруса следует, что перемещения и связаны зависимостью:

. (244)

Угол поворота поперечного сечения бруса в процессе движения определяется формулой

. (245)

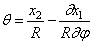
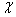
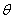
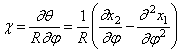
Изменение кривизны бруса равно производной от по дуге:

. (246)

Изгибающий момент в поперечном сечении кольца:

. (247)

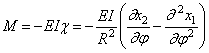
Теперь составим уравнение движения элемента 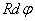бруса (рис.71,б).

Помимо перечисленных сил, на элемент действует также сила инерции:

,

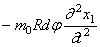
где 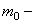масса единицы длины бруса.

Проектируя приложенные к элементу силы на радиус, получим

. (248)

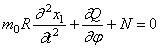
Равенство нулю суммы проекций всех сил на направление касательной приводит к уравнению:

. (249)

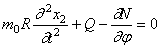
Уравнение моментов имеет вид

. (250)

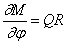
Исключим из (248) и (249) нормальную силу N , а поперечную силу Q заменим её значением из (250):

. (251)

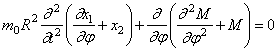
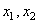
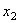
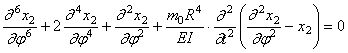
Подставляя сюда значение M из (247), получим уравнение движения в перемещениях , и, наконец, исключая один из компонентов перемещения, с помощью условия нерастяжимости (244) придём к уравнению, в которое входит единственная переменная :

. (252)

Решение уравнения движения (252) будем искать в виде

; .

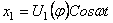
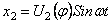
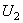
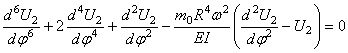
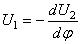
При этом для получается обыкновенное дифференциальное уравнение

, (253)

.

Согласно общим правилам решения дифференциальных уравнений, следует найти общее решение уравнения (253), включающее шесть постоянных, и подчинить его граничным условиям. На каждом конце бруса должны быть равны нулю либо компоненты перемещений 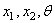, либо соответствующие им внутренние силы. Равенство нулю определителя системы, выражающей граничные условия, приводит к частотному уравнению.

Для замкнутого кольца граничные условия заменяются условиями периодичности, которые выполняются, если принять

; . (254)

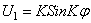
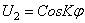
Подставляя (254) в (253), устанавливаем, что последнее удовлетворяется тождественно, если

. (255)

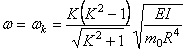
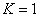
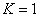
Формула (255) определяет частоты собственных колебаний кольца в своей плоскости. Значению соответствует нулевая частота, так как при формулы (254) описывают смещение кольца как жёсткого тела.

6.6.2. Колебания, перпендикулярные плоскости кольца

В этом случае положение поперечного сечения кольца в процессе движения характеризуется смещением 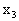его центра тяжести из плоскости кольца и углом поворота сечения х₄ (рис.72,а). В поперечном сечении кольца возникают изгибающие и крутящие моменты (рис.72,б), а также поперечная сила, перпендикулярная плоскости кольца.

Установим зависимость моментов от перемещений. Так как задача линейная, то рассмотрим сначала силовые факторы, связанные со смещением х₃, а затем — с х₄.

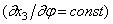
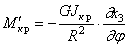
Если х₃ постоянно по длине окружности, то кольцо смещается как жёсткое целое, и внутренние силы не возникнут. Если х₃ изменяется в зависимости от центрального угла по линейному закону , то ось бруса превращается в винтовую линию, т.е. брус деформируется подобно витку пружины при растяжении. Известно, что в этом случае в поперечных сечениях возникает крутящий момент

,

где GJ _кр — крутильная жёсткость бруса.

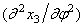
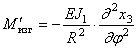
Если при этом отлична от нуля и вторая производная , то меняется кривизна бруса и возникает изгибающий момент

,

где J ₁ — момент инерции сечения относительно центральной оси, лежащей в плоскости кривизны.

Найдём силовые факторы, связанные с поворотом х₄. Если х₄ постоянно, то происходит осесимметричный изгиб кольца, причём в его сечениях возникает изгибающий момент

.

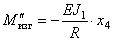
При переменном по длине повороте х₄ соседние сечения поворачиваются друг относительно друга и возникает крутящий момент

.

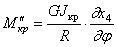
Суммируя силовые факторы, связанные с перемещениями х₃ и х_4, ,получаем

(256)

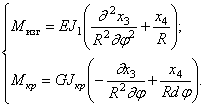
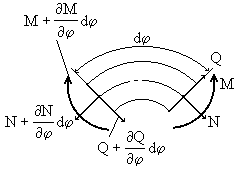
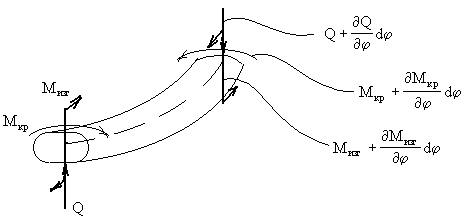
Составим уравнение движения элемента Rd бруса (рис.73).

Будем пренебрегать инерцией поворота элемента вокруг своей оси.

Условие динамического равновесия в направлении нормали к плоскости кольца приводит к уравнению:

. (257)

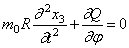
Сумма моментов относительно нормали к оси элемента:

. (258)

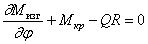
Сумма моментов относительно касательной к оси элемента:

. (259)

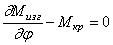
Исключая поперечную силу из (257) и (258) и заменяя моменты в полученном уравнении и уравнении (259) их значениями (256), приходим к системе уравнений, в которую входят только перемещения х₃ и х₄:

(260)

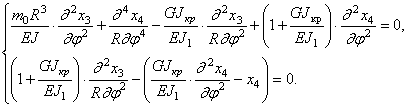
Ограничиваясь исследованием собственных колебаний замкнутого кольца, решение уравнений (260) можно представить в виде

x₃ = Acosk j × cos w t , x₄ = Bcosk j × cos w t . (261)

Подставляя значения (261) в уравнение движения (260), получим

(262)

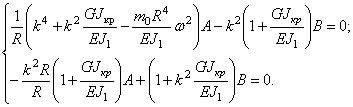
Из равенства нулю определителя этой системы получим частотное уравнение, корни которого — собственные частоты — таковы:

(263)

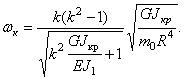
Наименьшая отличная от нуля частота соответствует k =2.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

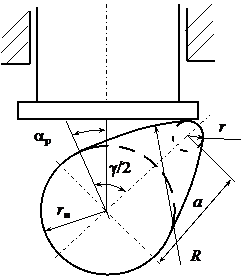
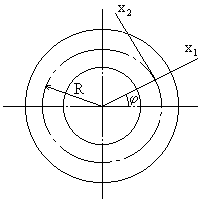
Крутильные колебания валов. Резонанс валов с з.к

В результате решения уравнений движения крутильных колебаний получим φ = φ₀ cos_plt

φ_{0 –} амплитуда колебаний вала с прикрепленной массой.

Р _φ – круговая собств. Частота крутилных колебаний

Резонанс валов с з.к.

Если число зубьев колеса z1, частота вращения вала n1, то возникает так называемая зубная частота колебаний f_з = n1z1/60

Явление резонанса имеет место тогда когда зубная частота совпадает с изгибными или крутильными колебаниями

Критические обороты валов.

Рассмотрим условия устойчивости валов. При изготовлении в результате погрешностей имеет место смещение центральных точек относительно оси вращения на r. Если вал отклонен на величину r, то возникает центробежная сила F_ц = mrw 2 и восстанавливающая сила упругости F_r = cr, где с- жесткость вала.

Рассмотрим два случая: 1) F_ц 2 w >1,3 w _кр w ≠0,7 w _кр / 1,3 w _кр

42.Опоры осей и валов. Общие понятия подшипников. Опорами называют уст-ва вала, предназначенные для восприятия нагрузки от вращ-ся эл-том машин(валов или осей с дет-ю) и передача нагрузок на корпус машин.Опоры включаю: -подшипники,-под-ки уплотнения,- эл-ты крепления.Подшипник-часть опоры,предн-я для поддерж-я валов и осей восприятия от них радиальных и осевых нагрузок и обеспеч-я их вращения или качания.При этом должно обеспеч-ся так же заданное положение вала или оси в простр-ве. Подш-ки разл-т :- по виду трений а)подш-ки скольжения(опорный уч-к вала скользит по поверхности втулки-вкладыша),б) подшипники качения,у кот трение скольжения заменено трением качения посредством установки шариков или роликов м/у кольцами. – дейсвия воспринимаемых сил а)радиальные подшипники(восприним-е радиаль-е нагруз-ки),б)упорные подш-ки( восп-е только осевые наг-ки),в) радиально-упорные( и те и др.)

43. Понятие трибологии, триботехники и видов трения. Расчёт и проек-е опор и подш-ков базируется на основных положениях трибологии.- наука о трении, изнашивании, смазке и взаимод-я контактир-х пов-тей при их взаимном перемещении. Триботехника- технич и технологич мероприятия по обеспечению оптимального функц-ния узлов трения. 2 вида трения:- внешнее, -внутреннее. Внешнее- совок-ть проц-в,протекаемых при относительном движ ТВ-х тел,в местах их прикосновения. Это мех-ие проц-ы, физ-хим-е, аккустич-е и др. проц.Под внутренним трением понимают проц-ы происх-ие в тв-х, жид-и и газообр-х телах при их деформации и приводящее к необратимому рассеиванию механической энергии деформации,т.е. к приобр-ю её во внутреннюю эн. Внутр-ее трение в жид. И газах опред-ся их вязкостью. По кинематичсекому признаку различают трение склольжения и трение качения.