Курсовая работа по теме,, Линейные уравнения с параметром»
В работе приводится пример введения параметра на уроке в 8 классе. Урок разработан полностью .
Скачать:
| Вложение | Размер |
|---|---|
| kursovaya_rabota1_lineynym_uravneniyam_s_parametrom.docx | 127.3 КБ |
Предварительный просмотр:
Государственное образовательное учреждение
дополнительного профессионального образования (повышения квалификации)
специалистов Московской области
Педагогическая Академия Последипломного Образования
Кафедра математических дисциплин
Методика решения задач с параметрами
«Линейные уравнения с параметром»
МБОУ Любучанская СОШ Чеховского района Московской области
Никулина Валентина Александровна
- Введение
- Место и цели задач с параметрами в школьном курсе математики.
- Линейное уравнение с параметром . Урок введения понятия параметра.
- Темы факультативных занятий в 8 классе.
- Материал к урокам
- Заключение
- Список литературы
В соответствии с распоряжением Правительства Российской Федерации от 29 декабря 2001 г. №1756-р об одобрении Концепции модернизации российского образования на период до 2010 г. на старшей ступени общеобразовательного школы предусматривается профильное обучение , ставится задача создания “ системы специализированной подготовки (профильного обучения) в старших классах общеобразовательной школы, ориентированной на индивидуализацию обучения и социализацию обучающихся, в том числе с учетом реальных потребностей рынка труда отработки гибкой системы профилей и кооперации старшей ступени школы с учреждениями начального, среднего и высшего профессионального образования ”.
Профильное обучение – средство дифференциации и индивидуализации обучения, позволяющее за счет изменений в структуре, содержании и организации образовательного процесса более полно учитываются интересы, склонности и способности учащихся, создавать условия для обучения старшеклассников в соответствии с их профессиональными интересами и намерениями в отношении продолжения образования. Профильная школа есть институциональная форма реализации этой цели. Это основная форма, однако перспективными в отдельных случаях могут стать иные формы организации профильного обучения, в том числе, выводящие реализацию соответствующих образовательных стандартов и программ за стены отдельного общеобразовательного учреждения.
Профильное обучение направлено на реализацию личностно-ориентированного учебного процесса. При этом существенно расширяются возможности выстраивания учеником индивидуальной образовательной траектории.
Элективные курсы – обязательные для посещения курсы по выбору учащихся, входящие в состав профиля обучения на старшей ступени школы. Элективные курсы реализуются за счет школьного компонента учебного плана и выполняют две функции. Одни из них могут «поддерживать» изучение основных профильных предметов на заданном профильным стандартом уровне. Например, элективный курс «Математическая статистика» поддерживает изучение профильного предмета экономики. Другие элективные курсы служат для внутрипрофильной специализации обучения и для построения индивидуальных образовательных траекторий. Например, курсы «Информационный бизнес», «Основы менеджмента» и др. в социально-гуманитарном профиле; курсы «Химические технологии», «Экология» и др. в естественнонаучном профиле. Количество элективных курсов, предлагаемых в составе профиля, должно быть избыточно по сравнению с числом курсов, которые обязан выбрать учащийся. По элективным курсам единый государственный экзамен не проводится.
К 15-16 годам у большинства учащихся складывается ориентация на сферу будущей профессиональной деятельности. Так, по данным социологических опросов, проведенных в 2002 году Центром социологических исследований Минобразования России, “профессиональное самоопределение тех, кто в дальнейшем намерен учиться в ПТУ или техникуме (колледже), начинается уже в 8-м классе и достигает своего пика в 9-м, а профессиональное самоопределение тех, кто намерен продолжить учебу в вузе, в основном складывается в 9-м классе”. При этом примерно 70-75% учащихся в конце 9-го класса уже определились в выборе возможной сферы профессиональной деятельности
Место и цели задач с параметрами в школьном курсе математики
Всё возрастающая популярность задач с параметрами далеко не случайна. Теоретическое изучение и математическое моделирование многообразных процессов из различных областей науки и практической деятельности человека часто приводят к достаточно сложным уравнениям и неравенствам или их системам содержащим параметры. Задачи с параметрами, предлагающиеся на конкурсных экзаменах, являются прообразом важных научно-исследовательских задач, которые предстоит решать будущему поколению. Такие задачи требуют глубокого понимания сути процесса, свободного владения различными математическими методами и скрупулёзного анализа.
Все рассмотренные задания в данной работе имеют цель – помочь учащимся составить представление о параметре, о том, что значит решить уравнение с ним. В самом начале знакомства с параметрами у учеников возникает психологический барьер, который обусловлен его противоречивыми характеристиками. С одной стороны, параметр в уравнении следует считать величиной известной, а с другой, конкретное значение параметра не дано. С одной стороны, параметр является величиной постоянной, а с другой может принимать различные значения. Получается, что параметр в уравнении – это «неизвестная величина», «переменная постоянная». Эти противоречивые высказывания точно отражают суть тех сложностей, которые нужно преодолеть ученикам.
В последнее время в материалах ЕГЭ и ГИА, предлагаются задания по теме: ,,Уравнения, содержащие параметр”. Некоторые учащиеся боятся даже браться за эти задачи, думая, что у них все равно не получиться. Стоит отметить, что навыки в решении уравнений и неравенств с параметром необходимы ученикам, желающим подготовиться для успешной сдачи централизованного тестирования и ЕГЭ, а также будет хорошим подспорьем для успешных выступлений на математических олимпиадах. Задачи такого типа вызывают затруднения у учащихся, так как практических заданий по данной теме в школьных учебниках мало.
Задачи с параметрами – эффективное упражнение для развития интеллекта, математического и логического мышления, умения анализировать, сравнивать, обобщать, способствуют формированию математической культуры. Каждое из заданий с параметрами представляет для учащихся небольшую исследовательскую работу, справившись с которой, ученик поднимается на одну ступеньку выше в своем понимании методов решения математических задач. Учащиеся, владеющие методами решения задач с параметрами, успешно справляются с другими задачами.
При решении задач с параметрами приходится все время производить несложные, но последовательные рассуждения, составлять для себя логическую схему решаемой задачи. Поэтому такие задачи – незаменимое средство для тренировки логического мышления. Их решение позволяет намного лучше понять обычные, без параметров, задачи. А привычка к математическим рассуждениям очень полезна при изучении высшей математики и использовании полученных знаний впоследствии.
Программа по математике средней общеобразовательной школы не уделяет большого внимания решению задач с параметрами. Следовательно, каждый учитель должен сам найти время на уроке или на факультативных занятиях для решения таких задач. Эти задачи представляют чисто математический интерес, способствуют интеллектуальному развитию учащихся, служат хорошим материалом для отработки навыков
Частичное решение проблемы (малочисленность задач с параметрами в школьном курсе математики) я вижу во введении факультативных занятий и элективных курсов по предпрофильной подготовке учащихся ,начиная с 8 класса, которые предусматривают формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, связанные существенным образом с математикой.
В школьном курсе математики одной из важных тем является тема «Линейные уравнения». Это первые уравнения с которыми учащиеся знакомятся в школьном курсе математики, начиная с первого класса , где решение уравнения сводится к нахождению неизвестного слагаемого, неизвестного уменьшаемого, вычитаемого, неизвестного множителя, делимого, делителя. Вводить уравнения с параметром нужно, начиная с линейных.
Урок введения понятия параметр. Линейное уравнение с параметром .
Тема занятия . Параметр. Линейное уравнение с параметром”
Задача занятия : ввести понятие параметра. Дать первые навыки решения линейных уравнений с параметром.
-Дайте определение линейного уравнения
-Что называется корнем уравнения?
-Что значит решить уравнение?
Введение понятие параметра на примере решения уравнения с параметром.
Для любого допустимого значения а указать как находится х.
Вопрос учащимся: Ребята, вы знаете как решать это уравнение ?
-В этом уравнении две неизвестных величины. Давайте решать уравнение перебором значений для а.
если а=2, то уравнение примет вид 2х-8=10-3х
Х=3,6(можно изобразить числовую прямую а и отмечать на ней значения х при заданном значении а )
Если а=-3, то уравнение примет вид -3х-8=-15-3х
0х=-7 уравнение решений не имеет
Если а=4,то уравнение примет вид 8х-8=40-3х
Нужно перебрать как можно больше значений а и указывать соответствующие им значения х . Вывод : перебором задачу не решить.
—А может мы делали какие-то одни и те же операции? (перенос из одной части в другую, нахождение неизвестного множителя)
—Какое выполняется всегда, заострять внимание на нем не нужно.
—А какое не всегда можно выполнить? (нахождение неизвестного множителя) Значит не при всех значениях а уравнение имеет корень.
Используя графическую интерпритацию записать ответ.
Итак решим уравнение :
ах+3х=5а+8 при любом а можно сделать перенос известных в одну сторону, а неизвестных в другую
х(а+3)=5а+8 при любом а можно х вынести за скобку
Чтобы найти х нужно (5а+8) разделить на (а+3), а это не всегда можно сделать.
Если а= -3, то уравнение примет вид ох=-7-решений нет
Если а#-3, то х=(5а+8)/(а+3). Желательно изобразить числовую прямую а и на ней отмечать все значения х , соответствующие данным значениям параметра а.
Ответ: если а=-3, то решений нет;
Если а#-3, то х=(5а+3)/(a+3)
Выполнение упражнений на закрепление.
Для любого допустимого значения а указать как находится х
-В уравнениях иногда некоторые коэффициенты заданы не конкретными числами, а обозначены буквами. Такие буквы называют параметрами. Предполагается, что эти параметры могут принимать любые числовые значения.
Решить уравнение с параметром – значит для любого допустимого значения параметра найти множество всех корней заданного уравнения.
Давайте составим алгоритм решения линейного уравнения с параметром .
-раскрыть скобки, если они есть
-перенести в одну сторону известные, в другую неизвестные (считаем х неизвестным)
-вынести х за скобки
-найти неизвестный множитель, учитывая допустимые значения параметра
Отработка навыка решения линейного уравнения с параметром
д) при каких значениях а уравнение 2(3х-2а)=2+ах не имеет решения ?
е) при каких значениях а уравнение 6(ах-1)-а=2(а+х)-7 имеет бесконечное множество решений ?
ж) при каких значениях а уравнение 2(а-2х)=ах+3 не имеет решения?
З) при каких значениях а уравнение 2(а+х)=3(1-х) имеет положительное решение?
и) при каких значениях а уравнение а(х-3)=2х+1 имеет решение , удовлетворяющее условию х
-Постарайтесь дать определение параметра своими словами
-Повторите алгоритм решения линейных уравнений с параметром
Темы факультативного курса,, Задачи с параметром” в 8 классе
Линейные уравнения
Автор работы: Пользователь скрыл имя, 21 Мая 2013 в 23:26, реферат
Краткое описание
Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.
Прикрепленные файлы: 1 файл
Линейные уравнения.doc
Линейные уравнения
Уравнения с одной переменной.
Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.
Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.
Решить уравнение — значит найти все его корни или доказать, что корней нет.
Уравнения называются равносильными, если все корни первого уравнения являются корнями второго уравнения и наоборот, все корни второго уравнения являются корнями первого уравнения или, если оба уравнения не имеют корней. Например, уравнения х-8=2 и х+10=20 равносильны, т.к. корень первого уравнения х=10 является корнем и второго уравнения, и оба уравнения имеют по одному корню.
При решении уравнений используются следующие свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Уравнение ах=b, где х – переменная, а и b – некоторые числа, называется линейным уравнением с одной переменной.
Если а¹0, то уравнение имеет единственное решение .
Если а=0, b=0, то уравнению удовлетворяет любое значение х.
Если а=0, b¹0, то уравнение не имеет решений, т.к. 0х=b не выполняется ни при одном значении переменной.
Пример 1. Решить уравнение: -8(11-2х)+40=3(5х-4)
Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим:
Пример 2. Решить уравнения:
Эти уравнения не являются линейными, но покажем, как можно решать такие уравнения.
3х2-5х=0; х(3х-5)=0. Произведение равно нулю, если один из множителей равен нулю, получаем х1=0; х2= .
Разложить на множители левую часть уравнения:
х2(х-2)-9(х-2)=(х-2)(х2-9)=(х- 2)(х-3)(х-3), т.е. (х-2)(х-3)(х+3)=0. Отсюда видно, что решениями этого уравнения являются числа х1=2, х2=3, х3=-3.
с) Представим 7х, как 3х+4х, тогда имеем: х2+3х+4х+12=0, х(х+3)+4(х+3)=0, (х+3)(х+4)=0, отсюда х1=-3, х2=- 4.
Пример 3. Решить уравнение: ½х+1ç+½х-1ç=3.
Напомним определение модуля числа:
Например: ½3½=3, ½0½=0, ½- 4½= 4.
В данном уравнении под знаком модуля стоят числа х-1 и х+1. Если х меньше, чем –1, то число х+1 отрицательное, тогда ½х+1½=-х-1. А если х>-1, то ½х+1½=х+1. При х=-1 ½х+1½=0.
а) Рассмотрим данное уравнение½х+1½+½х-1½=3 при х£-1, оно равносильно уравнению -х-1-х+1=3, -2х=3, х= , это число принадлежит множеству х£-1.
b) Пусть -1 ю х+1-х+1=3, 2¹3 уравнение не имеет решения на данном множестве.
с) Рассмотрим случай х>1.
х+1+х-1=3, 2х=3, х= . Это число принадлежит множеству х>1.
Ответ: х1=-1,5; х2=1,5.
Пример 4. Решить уравнение:½х+2½+3½х½=2½х-1½.
Покажем краткую запись решения уравнения, раскрывая знак модуля «по промежуткам».
–2 1, х+2+3х=2(х-1), 2х=- 4, х=-2Ï(1; +¥)
Пример 5. Решить уравнение: (а-1)(а+1)х=(а-1)(а+2), при всех значениях параметра а.
В этом уравнении на самом деле две переменных, но считают х–неизвестным, а а–параметром. Требуется решить уравнение относительно переменной х при любом значении параметра а.
Если а=1, то уравнение имеет вид 0×х=0, этому уравнению удовлетворяет любое число.
Если а=-1, то уравнение имеет вид 0×х=-2, этому уравнению не удовлетворяет ни одно число.
Если а¹1, а¹-1, тогда уравнение имеет единственное решение .
Ответ: если а=1, то х – любое число;
если а=-1, то нет решений;
Системы уравнений с двумя переменными.
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему — значит найти все ее решения или доказать, что их нет. Две системы уравнений называются равносильными, если каждое решение первой системы является решением второй системы и каждое решение второй системы является решением первой системы или они обе не имеют решений.
При решении линейных систем используют метод подстановки и метод сложения.
Пример 1. Решить систему уравнений:
Для решения этой системы применим метод подстановки. Выразим из первого уравнения х и подставим это значение во второе уравнение системы, получим
Пример 2. Решить систему уравнений:
Для решения этой системы применим метод сложения уравнений. 8х=16, х=2. Подставим значение х=2 в первое уравнение, получим 10-у=9, у=1.
Пример 3. Решить систему уравнений:
Эта система равносильна одному уравнению 2х+у=5, т.к. второе уравнение получается из первого умножением на 3. Следовательно, ей удовлетворяет любая пара чисел (х; 5-2х). Система имеет бесконечное множество решений.
Ответ: (х; 5-2х), х–любое.
Пример 4. Решить систему уравнений:
Умножим первое уравнение на –2 и сложим со вторым уравнением, получим 0×х+0×у=-6. Этому уравнению не удовлетворяет ни одна пара чисел. Следовательно, эта система не имеет решений.
Ответ: система не имеет решений.
Пример 5. Решить систему:
Из второго уравнения выражаем х=у+2а+1 и подставляем это значение х в первое уравнение системы, получаем . При а=-2 уравнение не а=-2 имеет решения, если а¹-2, то .
Ответ: при a=-2система не имеет решения,
при а¹-2 система имеет решение .
Пример 6. Решить систему уравнений:
Нам дана система из трех уравнений с тремя неизвестными. Применим метод Гаусса, который состоит в том, что равносильными преобразованиями приводят данную систему к треугольной форме. Прибавим к первому уравнению второе, умноженное на –2.
Далее к третьему уравнению системы прибавим второе, умноженное на –3,
наконец прибавим к этому уравнению уравнение у-z=-1, умноженное на 2, получим — 4z=-12, z=3. Итак получаем систему уравнений:
z=3, которая равносильна данной.
Система такого вида называется треугольной.
Курсовая работа: Методы решения уравнений, содержащих параметр
| Название: Методы решения уравнений, содержащих параметр Раздел: Рефераты по математике Тип: курсовая работа Добавлен 07:41:09 23 марта 2008 Похожие работы Просмотров: 7519 Комментариев: 21 Оценило: 3 человек Средний балл: 4.3 Оценка: неизвестно Скачать |

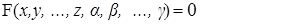 (F)
(F)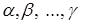 . При всякой допустимой системе значений параметров α0, β0, . γ0 уравнение (F) обращается в уравнение
. При всякой допустимой системе значений параметров α0, β0, . γ0 уравнение (F) обращается в уравнение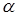 = α0,
= α0, 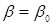 , .
, . 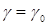 соответствующие значения функций (Х) образуют решение уравнения [1].
соответствующие значения функций (Х) образуют решение уравнения [1].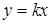 в зависимости от коэффициента
в зависимости от коэффициента 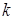 , который и является параметром.
, который и является параметром.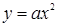 в зависимости от коэффициента
в зависимости от коэффициента 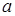 , и предлагается для решения задача на нахождение нулей функции, которая зависит от параметра. В разделе «дополнительные задачи» приводятся задания с параметром на исследование:
, и предлагается для решения задача на нахождение нулей функции, которая зависит от параметра. В разделе «дополнительные задачи» приводятся задания с параметром на исследование: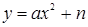 и
и 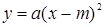 строятся предпосылки для решения уравнений, содержащих параметр, графическим методом (параллельный перенос).
строятся предпосылки для решения уравнений, содержащих параметр, графическим методом (параллельный перенос).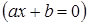 ставится ограничение на переменную a (a
ставится ограничение на переменную a (a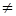 0). При изучении параметра, такие значения переменной и будем называть особыми, для которых будут соответствовать частные решения.
0). При изучении параметра, такие значения переменной и будем называть особыми, для которых будут соответствовать частные решения.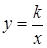 » при изучении функции
» при изучении функции 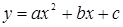 , ее свойств и графика предлагаются задачи, которые подготавливают ученика к решению уравнений с параметром, где требуется применение производной. А именно номера 474-475, где необходимо найти коэффициенты уравнения данной функции, если известно наибольшее или наименьшее значение функции. И также номера 483-488 в которых известно точки пересечения с осями координат. Особенно нужно выделить следующие номера: № 498-503, где от ученика требуется творческий подход к их решению.
, ее свойств и графика предлагаются задачи, которые подготавливают ученика к решению уравнений с параметром, где требуется применение производной. А именно номера 474-475, где необходимо найти коэффициенты уравнения данной функции, если известно наибольшее или наименьшее значение функции. И также номера 483-488 в которых известно точки пересечения с осями координат. Особенно нужно выделить следующие номера: № 498-503, где от ученика требуется творческий подход к их решению.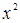 . Это потребует рассмотреть отдельно случаи, когда этот коэффициент равен нулю (см. [32], [33]).
. Это потребует рассмотреть отдельно случаи, когда этот коэффициент равен нулю (см. [32], [33]).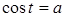 ,
, 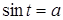 ,
, 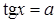 ,
, 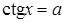 . Рассматривается решение этих уравнений в общем виде, и в зависимости от значения а рассматриваются частные случаи, причем ставится ограничение на множество значений переменной а (
. Рассматривается решение этих уравнений в общем виде, и в зависимости от значения а рассматриваются частные случаи, причем ставится ограничение на множество значений переменной а (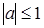 , для первых двух уравнений).
, для первых двух уравнений).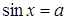 рассматривается принадлежность корня множествам
рассматривается принадлежность корня множествам 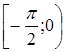 ,
, 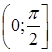 . И это тоже в какой-то степени уравнение с параметром решаемое методом «ветвлений» (пункт 4.1.1). Аналогично при рассмотрении уравнения
. И это тоже в какой-то степени уравнение с параметром решаемое методом «ветвлений» (пункт 4.1.1). Аналогично при рассмотрении уравнения 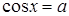 ,
, 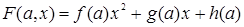 . Для таких уравнений всякое частное уравнение не выше второй степени принадлежит одному из следующих типов:
. Для таких уравнений всякое частное уравнение не выше второй степени принадлежит одному из следующих типов: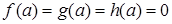 , тогда
, тогда 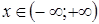 ,
,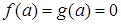 и
и 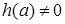 , тогда решений нет,
, тогда решений нет,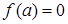 и
и 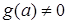 , тогда
, тогда 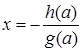 ,
,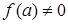 ,
, 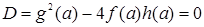 , тогда
, тогда 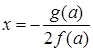 ,
,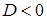 , тогда решений нет,
, тогда решений нет,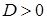 , тогда
, тогда 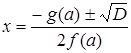 .
.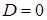 . На выделенных контрольными значениями промежутках допустимых значений параметра дискриминант имеет определенный знак, соответствующие частные уравнения принадлежат одному из двух последних типов.
. На выделенных контрольными значениями промежутках допустимых значений параметра дискриминант имеет определенный знак, соответствующие частные уравнения принадлежат одному из двух последних типов.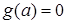 , выделяются типы бесконечных и пустых особых частных уравнений. Множеству значений параметра, для которых
, выделяются типы бесконечных и пустых особых частных уравнений. Множеству значений параметра, для которых 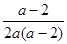 =
=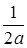 .
.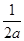 .
.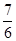 .
.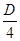 =(2а+ l)2 — (а — 1) (4а+3). После упрощений получаем
=(2а+ l)2 — (а — 1) (4а+3). После упрощений получаем 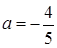 — второе контрольное значение параметра а. При этом если
— второе контрольное значение параметра а. При этом если 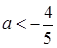 , то D 0,5 х1,2 = 0,5∙(1 ±
, то D 0,5 х1,2 = 0,5∙(1 ±  );
);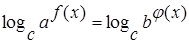 (c>0, c≠1) на области D (см. [1]).
(c>0, c≠1) на области D (см. [1]).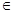 R, а > 0, b >0.
R, а > 0, b >0.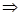 х = 3;
х = 3;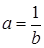 ,
, 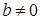 получим: уравнение
получим: уравнение 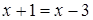 , которое не имеет решения;
, которое не имеет решения;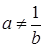 (а > 0, а ≠ 1, b >0, b ≠ 1) прологарифмируем исходное уравнение по основанию а, получим:
(а > 0, а ≠ 1, b >0, b ≠ 1) прологарифмируем исходное уравнение по основанию а, получим: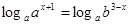 , х + 1 = (3 – х) log a b ,
, х + 1 = (3 – х) log a b , 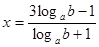 .
.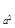
 (1 + х) = 3 log а
(1 + х) = 3 log а 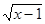 — log
— log 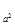
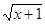 ,
,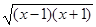 ,
,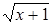 . Тогда получим
. Тогда получим 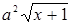 =
= 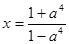 .
.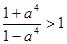 .
.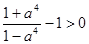 ,
, 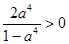 .
.