Курсовая работа уравнения и неравенства с параметром
ФБГОУ ВПО «Мордовский государственный
педагогический институт имени М.Е. евсевьева»
Кафедра математики и методики обучения математики
Методика формирования умений решать уравнения и неравенства с параметрами в курсе основной общеобразовательной школе
Автор курсовой работы:
студентка группы МДМ-110 А.И. Зимина
Специальность: 050201.65 «Математика» с дополнительной специальностью 050202 «Информатика»
. Теоретические основы линий уравнений и неравенств в школьном курсе математики
.1 Виды уравнений в школьном курсе математики
.2 Виды неравенств в школьном курсе математики
.3 Особенности решения уравнений с параметрами
.4 Особенности решения неравенств с параметрами
. Методические рекомендации к решению уравнений и неравенств с параметрами
Список используемой литературы
На современном этапе развития школьного образования становятся приоритетными развивающие цели обучения. В связи с этим при изучении математики особую значимость приобретает организованное обучение приемам мышления, рационального выполнения учебной деятельности, что исключительно важно при усвоении трудных тем и решении сложных задач таких, как уравнения и неравенства с параметрами. Именно недостаточная сформированность приемов учебной деятельности является одной из причин того, что большинство учащихся совершает ошибки или испытывает затруднения при решении даже несложных задач такого рода.
Изучением задач с параметрами, их роли в обучении, понятий, связанных с их решением, в разные годы занимались М.И. Башмаков , Г.В. Дорофеев, М.И. Зайкин, Т.А. Иванова, Г.Л. Луканкин, Я.Л. Крейнин, В.К. Марков, А.Г. Мордкович, Н.Х. Розов, Г.И. Саранцев, Р.А. Утеева и др. Многие из них подчеркивали важность обучения школьников приемам решения уравнений и неравенств с параметрами прежде всего в связи с необходимостью подготовки учащихся к выполнению работ итоговой аттестации и различного рода конкурсных испытаний. При этом большинство авторов характеризует задачи с параметрами как исследовательские задачи, требующие высокой логической культуры и техники исследования; как наиболее сложные в логическом и семантическом плане вопросы элементарной математики. В этой связи В.В. Вересова, В.И. Горбачев, Н.С. Денисова, В.Н. Литвиненко, А.Г. Мордкович, Т.Н. Полякова, Г.А. Ястребинецкий и др. справедливо замечают, что для описания процесса их решения необходимо использовать систему понятий, математических утверждений и фактов, определяемую фундаментальными математическими идеями; некоторые из них предпринимают попытки к ее разработке. Однако в многочисленных пособиях и руководствах справочного и методического характера для поступающих в вузы рассматриваются лишь частные приемы решения конкретных уравнений и неравенств с параметрами, чаще всего в рамках широкого спектра конкурсных заданий.
Уравнения и неравенства, содержащие параметр, не изучаются систематически в школьном курсе математики, а рассматриваются лишь отдельные их простейшие примеры. Поэтому методы и приемы решения таких задач большинству учащихся не известны.
Актуальность данной темы состоит в том, что анализируя экзаменационные работы по математике, приходишь к выводу, что за курс математики в общеобразовательной школе учащимися должны быть отработаны умения решения задач с параметрами. Кроме непосредственной подготовки учащихся к экзаменам по данному разделу математики (решение задач с параметрами), главная его задача — поднять на более высокий уровень изучение математики в школе, следующий за развитием умений и навыков решения определенного набора стандартных задач.
Объект исследования: процесс формирования умений решать уравнений и неравенств с параметрами в школьном курсе метематике основной школы.
Предмет исследования: уравнения и неравенства с параметрами.
Цель исследования: выделить виды, методы решения уравнений и неравенств с параметрами в школьном курсе математике.
Для достижения поставленной цели необходимо было решить следующие задачи:
) Изучить и проанализировать специальную литературу по проблеме исследования;
)Рассмотреть роль уравнений и неравенств в школьном курсе математике;
)Разработка методических рекомендаций к решению уравнений и неравенств с параметрами.
1. Теоретические основы линий уравнений и неравенств в школьном курсе математики
Ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики организовано в содержательно-методическую линию уравнений и неравенств. Здесь рассматриваются вопросы формирования понятий уравнения и неравенства, общих и частных методов их решения, взаимосвязи изучения уравнений и неравенств с числовой, функциональной и другими линиями школьного курса математики.
Выделенным областям возникновения и функционирования понятия уравнения в алгебре соответствуют три основных направления развертывания линии уравнений и неравенств в школьном курсе математики.
а) Прикладная направленность линии уравнений и неравенств раскрывается главным образом при изучении алгебраического метода решения текстовых задач. Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.
В настоящее время ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, неравенств и их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.
б) Теоретико-математическая направленность линии уравнений и неравенств раскрывается в двух аспектах: во-первых, в изучении наиболее важных классов уравнений, неравенств и их систем и, во-вторых, в изучении обобщенных понятий и методов, относящихся к линии в целом. Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений и неравенств связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение линии в целом, поскольку они описывают то общее, что имеется в процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование, которые также должны быть раскрыты в линии уравнений и неравенств.
в) Для линии уравнений и неравенств характерна направленность на установление связей с остальным содержанием курса математики. Эта линия тесно связана с числовой линией. Основная идея, реализуемая в процессе установления взаимосвязи этих линий, — это идея последовательного расширения числовой системы. Все числовые области, рассматриваемые в школьной алгебре и началах анализа, за исключением области всех действительных чисел, возникают в связи с решением каких-либо уравнений, неравенств, систем. Например, числовые промежутки выделяются неравенствами или системами неравенств. Области иррациональных и логарифмических выражений связаны соответственно с уравнениями (k-натуральное число, большее 1.
Связь линии уравнений и неравенств с числовой линией двусторонняя. Приведенные примеры показывают влияние уравнений и неравенств на развертывание числовой системы. Обратное влияние проявляется в том, что каждая вновь введенная числовая область расширяет возможности составления и решения различных уравнений и неравенств.
Линия уравнений и неравенств тесно связана также и с функциональной линией. Одна из важнейших таких связей приложения методов, разрабатываемых в линии уравнений и неравенств, к исследованию функции (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т.д.). С другой стороны, функциональная линия оказывает существенное влияние как на содержание линии уравнений и неравенств, так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений, неравенств и их систем.
.1 Виды уравнений в школьном курсе математике
уравнение неравенство математика
Понятие «уравнение » относится к важнейшим общематематическим понятиям.
Существуют различные трактовки понятия «уравнение».
И.Я. Виленкин и др. приводит логико — математическое определение уравнения. Пусть на множестве М зафиксирован набор алгебраических операций, х — переменная на М; тогда уравнением на множестве М относительно x называется предикат вида , где и — термы относительно заданных операций, в запись которого входит символ .Аналогично определиться уравнение от двух и более переменных.
Принятые в логики термины «терм» и «предикат» соответствуют такие термины школьной математики как «выражение» и «предложение с переменной». Поэтому наиболее близко к приведенному формальному определению можно считать следующее определение: «Предложение с переменной, имеющий вид равенства между двумя выражениями с этой переменной, называется уравнением». Такое определение приведено в учебнике «Алгебра и начала анализа» А.Н Колмогоров и др. Равенство с переменной называется уравнением. Значение переменной при котором равенство с переменной обращается в верное числовое равенство, называется корнем уравнения.
Часто, особенно в начале систематического курса алгебры, понятие уравнение вводится по средством выделение его из алгебраического метода решения задач. Например, в учебнике Ш.А.Алимова и др. понятие уравнение вводиться на материале текстовой задачи. Переход к понятию уравнения осуществляется на основе анализа некоторых формальных особенностей записи, выражающих содержание данной задачи в алгебраической форме: «Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением». Указываемый способ введения понятия уравнения соответствует еще одному компоненту понятия уравнения — прикладному.
Еще один подход к понятию уравнения получается при составления области определения уравнения и множества его корней. Например, в учебнике Д.К.Фадеева «Буквенное равенство, которое не обязательно превращается в верное числовое равенство при допустимых наборов букв, называется уравнение».
Можно встретить и третий вариант определения, роль которого проявляется при изучения графического метода решения уравнений: «Уравнение — это равенство двух функций».
Среди всех изучаемых в курсе математике типов уравнений В.И. Мишин выделяет сравнительно ограничение количество основных типов. к их числу относится: линейное уравнение с одним неизвестным, систему двух линейных уравнений с двумя неизвестными, квадратные уравнения, простейшие иррациональные и трансцендентные.
Ю.М.Колягин и др. классифицируют по виду функций, представляющих правую и левую части уравнений:
алгебраическим, если и — алгебраические функции;
трансцендентным, если хотя одним из функций и трансцендентная;
рациональным алгебраическим (или просто рациональным) , если алгебраические функции и рациональные;
иррациональным алгебраическим( или просто иррациональным), если хотя бы одна из алгебраических функций и иррациональная;
целым рациональным, если функция и целые рациональные;
дробным рациональным, если хотя бы одна из рациональных функций и дробная рациональная.
Уравнение , где — многочлен стандартного вида, называется линейным (первой степени), квадратным( во второй степени), кубическим (третьей степени) и вообще — ой степени, если многочлен , имеет соответственно первую, вторую, третью и вообще — ую степень.
В школе изучаются несколько типов уравнений. К их числу относятся: линейные уравнения с одной не известной, квадратные уравнения, иррациональные и трансцендентные уравнения, рациональные уравнения. Эти типы уравнений изучаются с большой тщательностью, для них указывается и доводиться до автоматизма выполнение алгоритма решения, указывается форма, в котором должен записываться ответ.
Виды уравнений и методы решения:
Уравнением с одной переменной, называется равенство, содержащее только одну переменную.
Корнем (или решением) уравнения называется такое значение переменной, при котором уравнение превращается в верное числовое равенство.
Найти все корни уравнения или доказать, что их нет — это значит решить уравнение.
Пример 1: Решить уравнение .
Квадратное уравнение — это уравнение вида , где коэффициенты a, b и c — любые действительные числа, причем а?0.
Корнями квадратного уравнения называют такие значения переменной, при которых квадратное уравнение обращается в верное числовое равенство.
Решить квадратное уравнение — значит найти все его корни или установить, что корней нет.
Пример 2: Решить уравнение
Данное уравнение можно решить либо через Теорему Виета, либо через дискриминант.
рациональные уравнения — уравнения вида
где и многочлены, атак же уравнения вида , где и — рациональные.
Пример 3: Решить уравнение
Иррациональные уравнения — это уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.
Пример 4: Решить уравнение
Возведем обе части в квадрат:
) Показательные и логарифмические уравнения
При решения показательных уравнений используются два основных метода: а) переход от уравнения к уравнению ;б) введения новых переменных. Иногда приходиться применять исскуственные приемы.
Логарифмические уравнения — решаются тремя методами, то есть переход от уравнения к уравнению — следствию ;метод введения новых переменных логарифмирования, то есть переход от уравнения к уравнению .
А так же во многих случаях при решения логарифмического уравнения приходиться использовать свойства логарифма произведения, частного, степени , корня.
.2 Виды неравенств в школьном курсе
В целом изучение неравенств в школьном курсе математики организовано так же, как и уравнений.
Отметим ряд особенностей изучения неравенств.
. Как и в случае уравнений отсутствует теория равносильности неравенств. Учащимся предлагаются её незначительные фрагменты, приведённые в содержании учебного материала.
. Большинство приёмов решения неравенств состоит в переходе от данного неравенства a>b к уравнению а=b и последующем переходе от найденных корней уравнения к множеству решений исходного неравенства. Например, такая ситуация возникает при решении рациональных неравенств методом интервалов, при решении простейших тригонометрических неравенств.
. В изучении неравенств большую роль играют наглядно — графические средства.
Два выражения (числовые или буквенные), соединённые одним из знаков: «больше» (>), «меньше» ( , a; или если a > b, то b b, то a + c > b + c; или если a b и c > d, то a + c > b + d . То есть, неравенства одного смысла (с одинаковым знаком > или b и c b — d . Или, если a d, то a — c b и m > 0, то ma > mb и a/m > b/m . То есть, обе части неравенства можно умножить или разделить на одно и то же положительное число. Неравенство при этом сохраняет свой знак.
. Если a > b и m алгебраические;
Алгебраические неравенства подразделяются на неравенства первой, второй, и т. д. степени.
Неравенство — алгебраическое, первой степени.
Неравенство — алгебраическое, второй степени.
Курсовая работа по теме: «Решение алгебраических неравенств с параметром методом областей».
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
3. Метод областей, его теоретическая основа…………………………
4. Примеры решения алгебраических неравенств с параметром методом областей……………………………………………………………
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ………………………….
Тема «Неравенства» занимает важное место в курсе алгебры. Она богата по содержанию, по способам и приемам решения неравенств, по возможностям ее применения при изучении ряда других тем элементарной алгебры. Это объясняется тем, что неравенства широко используются в различных разделах математики, в решении важных прикладных задач.
Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Некоторые Вузы также включают в экзаменационные билеты вступительного экзамена неравенства, которые часто бывают весьма сложными и требующими нестандартного подхода к решению. Этот один из наиболее трудных разделов элементарной математики рассматривается. Также неравенства с параметрами встречаются в материалах ЕГЭ по математике.
Все это послужило причиной выбора темы курсового исследования «Решение алгебраических неравенств с параметром методом областей».
Объект исследования: алгебраические неравенства.
Предмет исследования: алгебраические неравенства, содержащие параметр.
Целью курсовой работы является изучение алгебраических неравенств с параметром и их решение методом областей.
Для достижения поставленной цели необходимо решить ряд исследовательских задач.
Изучить математическую литературу для определения понятий «алгебраическое неравенство», «параметр», «алгебраическое неравенство с параметром».
Рассмотреть методы решения алгебраических неравенств с параметром.
Изучить особенности решения алгебраических неравенств методом областей.
Решить набор неравенств с параметром.
Теоретическая значимость курсовой заключается в систематизации теории решения алгебраических неравенств с параметром.
Практическая значимость курсовой работы заключается в том, что материал курсовой работы может быть использован для разработки элективного курса по математике в 9-11 классах.
Курсовая работа состоит из четырех параграфов. В первом параграфе рассматривается понятие алгебраического неравенства и его виды, понятие равносильного неравенства. Во втором параграфе рассматривается понятие параметра и методы решения алгебраических неравенств с параметром В третьем параграфе раскрывается описание решения алгебраических неравенств методом областей. В четвертом параграфе приведены примеры решения алгебраических неравенств методом областей.
АЛГЕБРАИЧЕСКИЕ НЕРАВЕНСТВА. ИХ ВИДЫ
Определение. Алгебраическим неравенством относительно переменной х называется высказывательная форма, имеющая вид , , где f ( x ), g ( x ) – рациональные выражения.
Область допустимых значений алгебраического выражения (сокращенно ОДЗ) это множество значений переменной, при которых это выражение определено.
Решением неравенства называют значение переменной, которое обращает его в верное числовое неравенство.
Решить неравенство означает установить все его решения или доказать, что решений не существует.
Основные свойства алгебраических неравенств
Выражается в том, что для любого числа а неравенства a > a и a a – неверные. Действительно, известно, что для любого числа a выполняется равенство a−a=0 , откуда в силу разностного определения равных чисел следует равенство a=a . Следовательно, a и a>a – неверные неравенства.
Например, 3 , — неверные неравенства.
Если числа a и b такие, что a , то b>a , и если a>b , то b .
Обоснуем его, обратившись к определению отношений «больше» и «меньше». Начнем с первой части. Так как a , то a−b – отрицательное число. При этом b−a=−(a−b) – положительное число, как число, противоположное отрицательному числу a−b . Следовательно, b>a . Аналогично доказывается и вторая часть рассматриваемого свойства.
Пример. Из неравенства 5 вытекает, что 11>5.
Если числа a , b и c таковы, что a и b , то a , и если a>b и b>c , то a>c .
Докажем его первое утверждение. Условия a и b означают, что a−b и b−c – отрицательные числа. Разность a−c можно представить как (a−b)+(b−c) , а это есть отрицательное число как сумма двух отрицательных чисел a−b и b−c , что следует из правила сложения отрицательных чисел . Таким образом, a−c – отрицательное число, откуда следует, что a , что и требовалось доказать. Абсолютно аналогично доказывается и вторая часть свойства транзитивности.
Пример. Из неравенств −1 и 5 можно заключить, что −1 .
Определение. Два неравенства с одной переменой f(x)>g(x) и h(x)>q(x) называются равносильными, если множества решений этих неравенств совпадают.
Свойства равносильности неравенств
Виды алгебраических неравенств
Линейное неравенство с одной неизвестной.
Определение. Линейным неравенством с одной переменной x называют неравенство вида ax+b > 0 , где вместо знака >, естественно может быть любой другой знак неравенства ( a и b – действительные числа , причем a≠0 . Мордкович А.Г. Алгебра 8 кл: Учебник. М. 2010.
Пример. 4(x − 1) ≥ 5 + x
Решение. ОДЗ: ; 4x − 4 ≥ 5 + x, 4x − x ≥ 5 + 4, 3x ≥ 9, x ≥ 3.
Определение. Это неравенство вида ax 2 +bx+c (вместо знака , ≥), где a , b и c – некоторые числа, причем a≠0 , а x – переменная (переменная может быть обозначена и любой другой буквой).
Пример. Решите неравенство
Определение. Рациональное неравенство – это неравенство, левая и правая части которого есть рациональные выражения относительно х. Никольский С. М. Алгебра 10 кл: Учебник. М. 2010.
Решение. Метод интервалов.
Определение 1. Неравенство, содержащее неизвестное под знаком корня называется иррациональным. Алимов Ш. А. Алгебра и начало математического анализа 10 кл: Учебник. М. 2012.
Виды иррациональных неравенств
1. равносильно системе в которой неравенство можно опустить и получается система
2. равносильно системе в которой неравенство можно опустить и получается система
3. равносильно совокупности двух систем
Решение. ОДЗ: следовательно ; 5-х x >-11.
Следовательно ответ (рисунок 2
ПОНЯТИЕ ПАРАМЕТРА В МАТЕМАТИКЕ. НЕРАВЕНСТВА С ПАРАМЕТРАМИ, МЕТОДЫ ИХ РЕШЕНИЯ
Понятие параметра в математике
Определение 1. Параметр (от греческого слова parametron — отмеривающий) — величина, значение которой служат для различения некоторого множества между собой. Мордкович А. Г. Алгебра 9 кл: Учебник. М. 2013.
Основные типы задач с параметром
Тип 1. Неравенства, которые необходимо решить либо для любого значения параметра, либо для значений параметра, принадлежащих заранее оговорённому множеству. Этот тип задач является базовым при овладении темой «Неравенства с параметрами».
Тип 2. Н еравенства, для которых требуется определить имеет неравенство решения или нет в зависимости от значения параметра.
Тип 3. Неравенства, для которых требуется найти все те значения параметра, при которых решения неравенства обладают заданными свойствами.
Основные методы решения задач с параметром
Метод 1. (аналитический) Этот способ так называемого прямого решения, повторяющего стандартные способы нахождения ответа в задачах без параметра.
Пример 1. Решите неравенство при всех значениях параметра а
(а + 1)х – 3а + 1 ≤ 0.
Решение. (а + 1)х – 3а + 1 ≤ 0 – линейное неравенство.
а+1=0; 0х+3-1 ≤ 0, 2 ≤ 0 — Нет решения.
Ответ. Если a , то , если а=-1 , то решений нет; если a >-1 , то .
Пример 2. Решите неравенство при всех значениях параметра а
Решение. Преобразуем исходное неравенство , . Домножим на (-1) обе части неравенства, получим .
Исследуем возможные случаи для параметра а:
1 случай. Пусть или а ∈ (-∞; 0)ᴗ(1; +∞) . Тогда .
2 случай. Пусть , т.е. а = 0 . Тогда x – любое действительное число.
3 случай. Пусть или а ∈ (0; 1) . Тогда .
Пример 3. При всех значениях параметра a решите неравенство
Решение. При любом фиксированном значении a это обычное рациональное неравенство. Это неравенство равносильно неравенству
Для этого на числовой оси надо расположить точки а и а+2. Очевидно, что при любом значении a число a+2 больше, чем a . Эти точки будут являться нулями параболы , ветви которой направленный вверх (рисунок 3).
Получаем, что значения функции будут неотрицательны в промежутках и .
Ответ. при любом а .
Метод 2. (графический) В зависимости от задачи рассматриваются графики в координатной плоскости (х;у), или в координатной плоскости (х;а).
Пример. Решить неравенство при всех значениях а
Решение. Перенесем х в левую часть неравенства. Строим график функции у = |2 – |x||+ x (рисунок 4) и рассматриваем все возможные случаи расположения прямой у = а.
Ответ. Если , то решений нет; если , то ; если , то ; если а=2 , то ; если , то .
МЕТОД ОБЛАСТЕЙ, ЕГО ТЕОРЕТИЧЕСКАЯ ОСНОВА
Метод областей на координатной плоскости
В основе метода областей на координатной плоскости лежит метод координат.
Определение. Геометрическим местом точек (ГМТ) плоскости называется совокупност0ь точек, обладающих одним или несколькими общими (характеристическими) свойствами. Днепровская О. А., Калабина Е. В., Ермак Н. В. Аналитическая геометрия на плоскости.
Определение. Аналитическим условием, определяющим фигуру (ГМТ) в данной системе координат, называется уравнение, неравенство, их системы или совокупности, которым удовлетворяют координаты любой точки, принадлежащей фигуре, и не удовлетворяют координаты любой точки, не принадлежащей фигуре.
Аналитическое условие прямой – уравнение
Точки первой координатной четверти задаются системой неравенств
Окружность определяется уравнением
Метод координат позволяет
Характеризовать посредством координат точек геометрические объекты, задавать их аналитические условия;
Использавать аппарат алгебры для решения геометрических задач;
Алгоритмизировать процесс решения задач и доказательства теорем.
Методом координат решаются аналитические задачи двух типов
По геометрическим свойствам фигуры составить ее аналитическое условие.
По заданному аналитическому условию фигуры исследовать ее свойства.
Задачи с параметром в основном относятся ко второму типу.
При решении задач второго типа необходимо учитывать
Уравнение с двумя неизвестными F ( x , y )=0 задает множество точек на плоскости.
Задание фигуры уравнением называется явным.
Задание фигуры уравнением называется неявным.
Задание фигуры системой уравнений называется параметрическим заданием.
Если аналитическому условию фигуры удовлетворяют координаты конечного числа точек, то фигура вырожденная (например, ).
Если аналитическому условию фигуры не удовлетворяют действительные координаты точки, то фигура мнимая (например, ).
Если аналитическое условие фигуры представимо как произведение множителей, сравнимых с нулем, то фигура распавшаяся (например, ).
Для изображения на координатной плоскости Оху множества решений неравенств с двумя переменными используется построение на координатной плоскости множества точек, у которых координаты удовлетворяют данным неравенствам. При решении неравенства f(x; у) ≥ 0 , равносильного смешанной совокупности применяется метод областей, являющийся обобщением метода интервалов на случай двух переменных. Для этого вначале находят все нули выражения f ( x ; у) , то есть все такие точки, координаты которых удовлетворяют уравнению f ( x ; у) =0 . В общем случае уравнение f ( x ; у)=0 задает некоторую кривую (или несколько кривых) на плоскости Оху . Полученные кривые разбивают плоскость на множества, для координат всех точек которых выражение f ( x ;у) имеет постоянный знак. Далее отбирают требуемые подмножества, у которых координаты точек удовлетворяют неравенству f ( x ;у) >0 . Это можно сделать подстановкой координат произвольной точки из рассматриваемого подмножества в выражение f ( x ; у ).
Простейшим является случай, когда f(x;у)=Ах +By+С, где , то есть числа А и В одновременно не обращаются в нуль. Уравнение Ах+By+С=0 задает прямую, которая разбивает координатную плоскость на две полуплоскости, для координат точек одной из которых выполняется неравенство Ах+ By+С> 0 , а в другой неравенство Ах+Ву+С .
Уравнение , где a, b, R — заданные числа, причем R>0 , задает на координатной плоскости окружность С радиуса R с центром в точке (а; b), а неравенствам и удовлетворяют все те и только те точки, которые расположены соответственно внутри области, ограниченной окружностью С , и снаружи.
Пример. Решите неравенство
Решение. ОДЗ этого неравенства состоит из точек координатной плоскости, удовлетворяющих неравенству или , т.е. . Пунктирной линией изображаем окружность с центром в точке (-2,0) радиуса 2 (рисунок 5) .
Курсовая работа: Методы решения уравнений, содержащих параметр
| Название: Методы решения уравнений, содержащих параметр Раздел: Рефераты по математике Тип: курсовая работа Добавлен 07:41:09 23 марта 2008 Похожие работы Просмотров: 7519 Комментариев: 21 Оценило: 3 человек Средний балл: 4.3 Оценка: неизвестно Скачать |
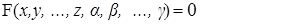 (F)
(F)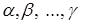 . При всякой допустимой системе значений параметров α0, β0, . γ0 уравнение (F) обращается в уравнение
. При всякой допустимой системе значений параметров α0, β0, . γ0 уравнение (F) обращается в уравнение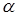 = α0,
= α0, 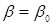 , .
, . 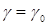 соответствующие значения функций (Х) образуют решение уравнения [1].
соответствующие значения функций (Х) образуют решение уравнения [1].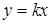 в зависимости от коэффициента
в зависимости от коэффициента 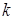 , который и является параметром.
, который и является параметром.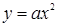 в зависимости от коэффициента
в зависимости от коэффициента 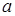 , и предлагается для решения задача на нахождение нулей функции, которая зависит от параметра. В разделе «дополнительные задачи» приводятся задания с параметром на исследование:
, и предлагается для решения задача на нахождение нулей функции, которая зависит от параметра. В разделе «дополнительные задачи» приводятся задания с параметром на исследование: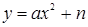 и
и 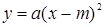 строятся предпосылки для решения уравнений, содержащих параметр, графическим методом (параллельный перенос).
строятся предпосылки для решения уравнений, содержащих параметр, графическим методом (параллельный перенос).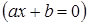 ставится ограничение на переменную a (a
ставится ограничение на переменную a (a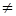 0). При изучении параметра, такие значения переменной и будем называть особыми, для которых будут соответствовать частные решения.
0). При изучении параметра, такие значения переменной и будем называть особыми, для которых будут соответствовать частные решения.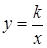 » при изучении функции
» при изучении функции 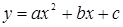 , ее свойств и графика предлагаются задачи, которые подготавливают ученика к решению уравнений с параметром, где требуется применение производной. А именно номера 474-475, где необходимо найти коэффициенты уравнения данной функции, если известно наибольшее или наименьшее значение функции. И также номера 483-488 в которых известно точки пересечения с осями координат. Особенно нужно выделить следующие номера: № 498-503, где от ученика требуется творческий подход к их решению.
, ее свойств и графика предлагаются задачи, которые подготавливают ученика к решению уравнений с параметром, где требуется применение производной. А именно номера 474-475, где необходимо найти коэффициенты уравнения данной функции, если известно наибольшее или наименьшее значение функции. И также номера 483-488 в которых известно точки пересечения с осями координат. Особенно нужно выделить следующие номера: № 498-503, где от ученика требуется творческий подход к их решению.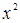 . Это потребует рассмотреть отдельно случаи, когда этот коэффициент равен нулю (см. [32], [33]).
. Это потребует рассмотреть отдельно случаи, когда этот коэффициент равен нулю (см. [32], [33]).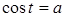 ,
, 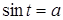 ,
, 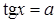 ,
, 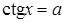 . Рассматривается решение этих уравнений в общем виде, и в зависимости от значения а рассматриваются частные случаи, причем ставится ограничение на множество значений переменной а (
. Рассматривается решение этих уравнений в общем виде, и в зависимости от значения а рассматриваются частные случаи, причем ставится ограничение на множество значений переменной а (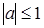 , для первых двух уравнений).
, для первых двух уравнений).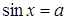 рассматривается принадлежность корня множествам
рассматривается принадлежность корня множествам 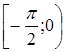 ,
, 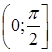 . И это тоже в какой-то степени уравнение с параметром решаемое методом «ветвлений» (пункт 4.1.1). Аналогично при рассмотрении уравнения
. И это тоже в какой-то степени уравнение с параметром решаемое методом «ветвлений» (пункт 4.1.1). Аналогично при рассмотрении уравнения 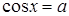 ,
, 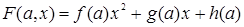 . Для таких уравнений всякое частное уравнение не выше второй степени принадлежит одному из следующих типов:
. Для таких уравнений всякое частное уравнение не выше второй степени принадлежит одному из следующих типов: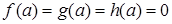 , тогда
, тогда 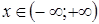 ,
,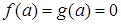 и
и 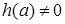 , тогда решений нет,
, тогда решений нет,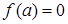 и
и 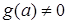 , тогда
, тогда 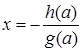 ,
,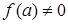 ,
, 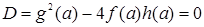 , тогда
, тогда 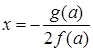 ,
,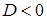 , тогда решений нет,
, тогда решений нет,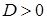 , тогда
, тогда 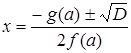 .
.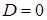 . На выделенных контрольными значениями промежутках допустимых значений параметра дискриминант имеет определенный знак, соответствующие частные уравнения принадлежат одному из двух последних типов.
. На выделенных контрольными значениями промежутках допустимых значений параметра дискриминант имеет определенный знак, соответствующие частные уравнения принадлежат одному из двух последних типов.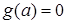 , выделяются типы бесконечных и пустых особых частных уравнений. Множеству значений параметра, для которых
, выделяются типы бесконечных и пустых особых частных уравнений. Множеству значений параметра, для которых 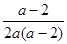 =
=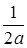 .
.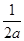 .
.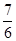 .
.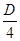 =(2а+ l)2 — (а — 1) (4а+3). После упрощений получаем
=(2а+ l)2 — (а — 1) (4а+3). После упрощений получаем 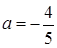 — второе контрольное значение параметра а. При этом если
— второе контрольное значение параметра а. При этом если 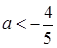 , то D 0,5 х1,2 = 0,5∙(1 ±
, то D 0,5 х1,2 = 0,5∙(1 ±  );
);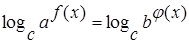 (c>0, c≠1) на области D (см. [1]).
(c>0, c≠1) на области D (см. [1]).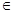 R, а > 0, b >0.
R, а > 0, b >0.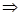 х = 3;
х = 3;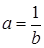 ,
, 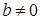 получим: уравнение
получим: уравнение 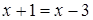 , которое не имеет решения;
, которое не имеет решения;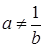 (а > 0, а ≠ 1, b >0, b ≠ 1) прологарифмируем исходное уравнение по основанию а, получим:
(а > 0, а ≠ 1, b >0, b ≠ 1) прологарифмируем исходное уравнение по основанию а, получим: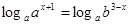 , х + 1 = (3 – х) log a b ,
, х + 1 = (3 – х) log a b , 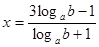 .
.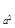
 (1 + х) = 3 log а
(1 + х) = 3 log а 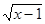 — log
— log 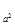
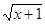 ,
,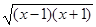 ,
,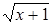 . Тогда получим
. Тогда получим 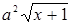 =
= 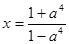 .
.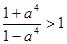 .
.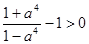 ,
, 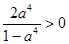 .
.