Квадратичная форма уравнения второго порядка

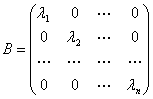
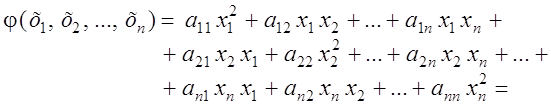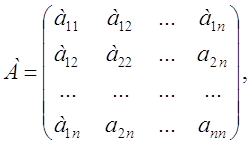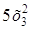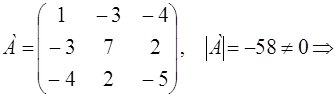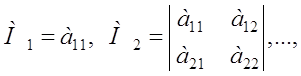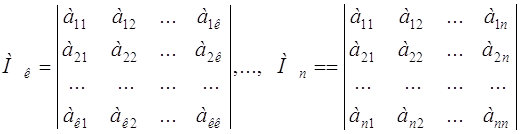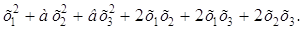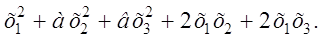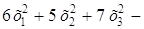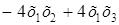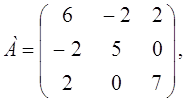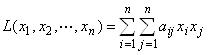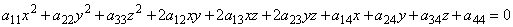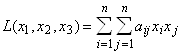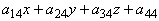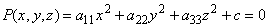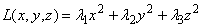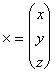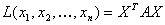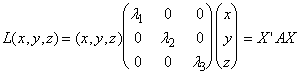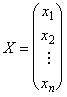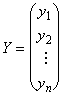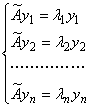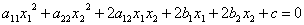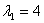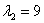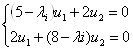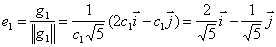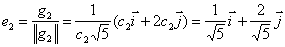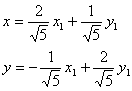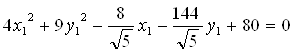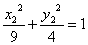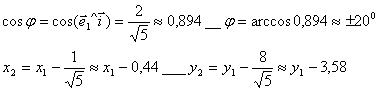Приведение кривой второго порядка к каноническому виду

Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.

Решение. Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:

Характеристическое уравнение:
; λ₁=-2, λ₂=8. Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x₁ 2 -2y₁ 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. .
Собственный вектор, отвечающий числу λ=-2 при x₁=1: x ₁=(1,-1).
В качестве единичного собственного вектора принимаем вектор , где – длина вектора x ₁.
Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы
.
x ₂=(1,1); .
Итак, имеем новый ортонормированный базис ( i ₁, j ₁).
По формулам (5) пункта 4.3.3. переходим к новому базису:
или

Задание. Привести к каноническому виду уравнение линии 17x 2 + 12xy + 8y 2 — 20 = 0.
Решение.Пример 2

Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение

Задание. Привести уравнение к каноническому виду: 16x 2 — 9y 2 -64x — 8y +199 = 0.
Решение.Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение

Кривые второго порядка. Квадратичные формы

1. Понятие квадратичной формы и способы ее записи

2. Знакоопределенность квадратичных форм

3. Критерии положительной и отрицательной определенностей

1. Понятие квадратичной формы и способы ее записи

Квадратичной формой j (х₁, х₂, …, x_n) n действительных переменных х₁, х₂, …, x_n называется сумма вида

,(1)

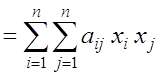
где a_ij – некоторые числа, называемые коэффициентами. Не ограничивая общности, можно считать, что a_ij = a_ji.

Квадратичная форма называется действительной, если a_ij Î ГR. Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (1) соответствует единственная симметричная матрица

то есть А Т = А. Следовательно, квадратичная форма (1) может быть записана в матричном виде j(х) = х Т Ах, где

И, наоборот, всякой симметричной матрице (2) соответствует единственная квадратичная форма с точностью до обозначения переменных.

Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма называется невырожденной, если невырожденной является ее матрица А. (напомним, что матрица А называется невырожденной, если ее определитель не равен нулю). В противном случае квадратичная форма является вырожденной.

Записать матрицу квадратичной формы

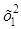
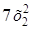
j (х₁, х₂, x₃) = – 6х₁х₂ – 8х₁х₃ + + 4х₂х₃ –

и найти ее ранг.

квадратичная форма невырождена.

2. Знакоопределенность квадратичных форм

Квадратичная форма (1) называется положительно определенной (или строго положительной), если j(х) > 0, для любого х = (х₁, х₂, …, x_n), кроме х = (0, 0, …, 0).

Матрица А положительно определенной квадратичной формы j(х) также называется положительно определенной. Следовательно, положительно определенной квадратичной форме соответствует единственная положительно определенная матрица и наоборот.

Квадратичная форма (1) называется отрицательно определенной (или строго отрицательной), если j(х) 2 требуются специальные критерии для проверки знакоопределенности квадратичной формы. Рассмотрим их.

Главными минорами квадратичной формы называются миноры:

то есть это миноры порядка 1, 2, …, n матрицы А, расположенные в левом верхнем углу, последний из них совпадает с определителем матрицы А.

3. Критерий положительной и отрицательной определенности

Критерий положительной определенности (критерий Сильвестра)

Для того чтобы квадратичная форма j(х) = х Т Ах была положительно определенной, необходимо и достаточно, что все главные миноры матрицы А были положительны, то есть:

Критерий отрицательной определенности

Для того чтобы квадратичная форма j(х) = х Т Ах была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного – отрицательны, то есть:

При каких значениях а и в квадратичная форма будет положительно определенной?

j (х₁, х₂, x₃) =

Построим матрицу А и найдем ее главные миноры.

М₁ = 1 > 0,

= а – 1 > 0 Þ а > 1.

= ав – а – в > 0 Þ в > .

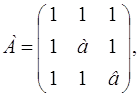
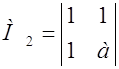
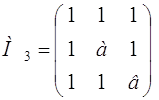
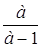
а > 1, в > .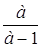

При каких значениях а и в квадратичная форма будет отрицательно определенной?

j (х₁, х₂, x₃) =

М₁ = –1 0 Þ а – .

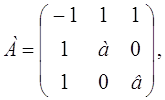
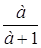
а –.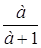

Доказать, что квадратичная форма

j (х₁, х₂, x₃) =

Воспользуемся критерием Сильвестра. Построим матрицу А и найдем главные миноры матрицы А.

М₁ = 6 > 0, 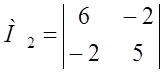= 26 > 0, М₃ = ú А ç = 162 > 0

положительно определенная квадратичная форма.

1. Гусак А. А. Аналитическая геометрия и линейная алгебра.– Мн.: Тетрасистемс, 1998.

2. Овсеец М. И., Светлая Е. М. Сборник задач по высшей математике. Учебное издание.– Мн.: ЧИУиП, 2006.– 67 с.

69. Квадратичные формы и их приведение к каноническому виду

При рассмотрении евклидового пространства мы вводили определение квадратичной формы. С помощью некоторой матрицы

Строится многочлен второго порядка вида

Который называется квадратичной формой, порождаемой квадратной матрицей А.

Квадратичные формы тесно связаны с поверхностями второго порядка в n — мерном евклидовом пространстве. Общее уравнение таких поверхностей в нашем трехмерном евклидовом пространстве в декартовой системе координат имеет вид:

Верхняя строка — это не что иное, как квадратичная форма, если положить x1=x, x2=y, x3=z:

— симметричная матрица (aij = aji)

Положим для общности, что многочлен

Есть линейная форма. Тогда общее уравнение поверхности есть сумма квадратичной формы, линейной формы и некоторой постоянной.

Основной задачей теории квадратичных форм является приведение квадратичной формы к максимально простому виду с помощью невырожденного линейного преобразования переменных или, другими словами, замены базиса.

Вспомним, что при изучении поверхностей второго порядка мы приходили к выводу о том, что путем поворота осей координат можно избавиться от слагаемых, содержащих произведение xy, xz, yz или xixj (i¹j). Далее, путем параллельного переноса осей координат можно избавиться от линейных слагаемых и в конечном итоге свести общее уравнение поверхности к виду:

В случае квадратичной формы приведение ее к виду

Называется приведением квадратичной формы к каноническому виду.

Поворот осей координат есть не что иное, как замена одного базиса другим, или, другими словами, линейное преобразование.

Запишем квадратичную форму в матричном виде. Для этого представим ее следующим образом:

L(x, y,z) = x(a11x+a12y+a13z)+

Введем матрицу — столбец

Тогда 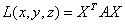— где X T =(x, y,z)

— матричная форма записи квадратичной формы. Эта формула, очевидно, справедлива и в общем случае:

Канонический вид квадратичной формы означает, очевидно, что матрица А имеет диагональный вид:

Рассмотрим некоторое линейное преобразование X = SY, где S — квадратная матрица порядка n, а матрицы — столбцы Х и У есть:

Матрица S называется матрицей линейного преобразования. Отметим попутно, что всякой матрице n-ного порядка при заданном базисе соответствует некоторый линейный оператор.

Линейное преобразование X = SY заменяет переменные x1, x2, x3 новыми переменными y1, y2, y3. Тогда:

где B = S T A S

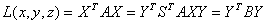
Задача приведения к каноническому виду сводится к отысканию такой матрицы перехода S, чтобы матрица В приобрела диагональный вид:

(*)

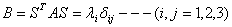
Итак, квадратичная форма с матрицей А после линейного преобразования переменных переходит в квадратичную форму от новых переменных с матрицей В.

Обратимся к линейным операторам. Каждой матрице А при заданном базисе соответствует некоторый линейный оператор А. Этот оператор имеет, очевидно, некоторую систему собственных чисел и собственных векторов. Причем, отметим, что в евклидовом пространстве система собственных векторов будет ортогональна. Мы доказывали на предыдущей лекции, что в базисе собственных векторов матрица линейного оператора имеет диагональный вид. Формула (*), как мы помним, это формула преобразования матрицы линейного оператора при смене базиса. Положим, что собственные вектора линейного оператора А с матрицей А — это вектора у1, y2, . yn.

Т. е.

А это означает, что если собственные вектора у1, y2, . yn взять за базис, то матрица линейного оператора в этом базисе будет диагональной

Или В = S-1 А S, где S – матрица перехода от первоначального базиса <E> к базису <Y>. Причем в ортонормированном базисе матрица S будет ортогональной.

Т. о. для приведения квадратичной формы к каноническому виду необходимо найти собственные числа и собственные векторы линейного оператора А, имеющего в первоначальном базисе матрицу А, которая порождает квадратичную форму, перейти к базису собственных векторов и в новой системе координат построить квадратичную форму.

Обратимся к конкретным примерам. Рассмотрим линии второго порядка.

или

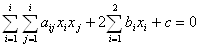
С помощью поворота осей координат и последующего параллельного переноса осей это уравнение можно привести к виду ( переменные и коэффициенты переобозначены х1 = х, х2 = у):

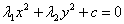
1) если линия центральная, l1 ¹ 0, l2 ¹ 0

2) если линия нецентральная, т. е. один из li = 0.

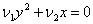
Напомним виды линий второго порядка. Центральные линии:

1) эллипс;

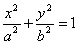
2) гипербола;

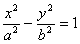
3) точка;

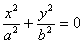
4) две пересекающиеся прямые.

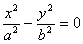
5) х2 = а2 две параллельные линии;

6) х2 = 0 две сливающиеся прямые;

7) у2 = 2рх парабола.

Для нас представляют интерес случаи 1), 2), 7).

Рассмотрим конкретный пример.

Привести к каноническому виду уравнение линии и построить ее:

5х2 + 4ху + 8у2 — 32х — 56у + 80 = 0.

Матрица квадратичной формы есть . Характеристическое уравнение:

Его корни:

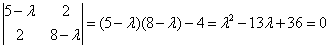
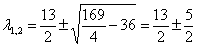
Найдем собственные векторы:

При l1 = 4: 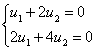u1 = -2u2; u1 = 2c, u2 = — c или g1 = c1(2I – J).

При l2 = 9: 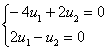2u1 = u2; u1 = c, u2 = 2c или g2 = c2(I+2J).

Нормируем эти векторы:

Составим матрицу линейного преобразования или матрицу перехода к базису g1, g2:

— ортогональная матрица!

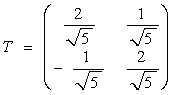
Формулы преобразования координат имеют вид:

или

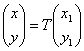
Подставим в наше уравнение линии и получим:

Сделаем параллельный перенос осей координат. Для этого выделим полные квадраты по х1 и у1:

Обозначим . Тогда уравнение приобретет вид: 4х22 + 9у22 = 36 или

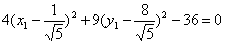
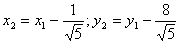
Это эллипс с полуосями 3 и 2. Определим угол поворота осей координат и их сдвиг для того, чтобы построить эллипс в старой системе.

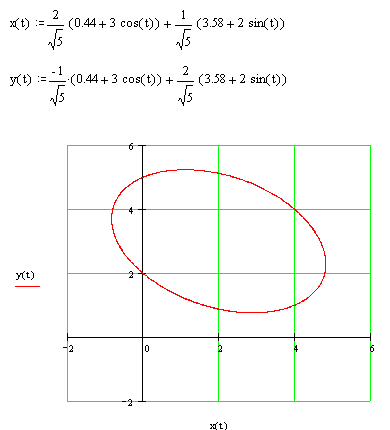
Построим:

Проверка: при х = 0: 8у2 — 56у + 80 = 0 у2 – 7у + 10 = 0. Отсюда у1,2 = 5; 2

При у =0: 5х2 – 32х + 80 = 0 Здесь нет корней, т. е. нет точек пересечения с осью Х!