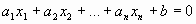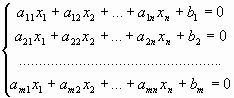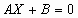Квадратная система линейных уравнений это

Квадратная система линейных уравнений с определителем основной матрицы, отличным от нуля

Квадратная система линейных уравнений с определителем основной матрицы, отличным от нуля

• Система квадратов следующего линейного уравнения Ненулевая основная матричная лемма. Давайте дадим квадрат Линейная система уравнений \ X \ + CL12X2 + … + CLinXn = С.10) \ X \ + an2X2 + … + appxn = bn Ненулевой определитель A главной матрицы A = ах шум ^ 22 ар2 С.11) Такие системы дополнительно включают в себя и найдите это решение.

• Сначала докажите, что система C.10) может делать. Существует только одно решение (то есть, доказать единственность решения В.10) Предполагая его существование). Предположим, что существует n чисел xi, X2, …, xn. Подставляя эти числа в систему, C.10) весь баланс Выражение этой системы меняется на идентичность (то есть Второе решение системы C.10) xi, x2, …, xn).

Затем умножьте тождества C.10), алгебраические дополнения A \ j ^ A ^ j, …, Anj соответственно. Людмила Фирмаль

Сложите с j-ro элементом определителя столбца A матрицы C.11) Далее получаем идентификатор полученный таким образом ( Число j равно 1, 2, …, n) г = 1 aniAnj) = bnAnj. сумма произведений элементов в столбце r-ro соответствует Существующее алгебраическое дополнение элементов последовательности j-ro r = j для r f j и равна определителю A матрицы C.11) Получить из последнего равенства XjA = bAq + b2A2j + … + bnAnj. С.12) 8) гл. См.

Свойство 4 ° в подразделе 4 §2. 1. Отображать с помощью Aj (pi) (или проще с помощью Aj) Определитель, полученный из определителя А основной матрицы C.11) Заменить j-й столбец на пустой столбец-член B \, b, …, bn (если вы хотите сохранить все остальные столбцы без изменений Cov L).

Обратите внимание, что в правой части C.12 есть именно определители. Aj (pi) 9) это равенство принимает вид (J = 1, 2, …, n). С.13) Определитель Λ матрицы C.11) не равен нулю и равен Эквивалент C.13) Xj = ^ (i =! ‘2’¦ • ¦’ «) ¦ С.14) Таким образом, решение x1, x2, …, xn системы C.10 имеет вид Кроме определителя A основной матрицы C.11) Если la существует, это решение однозначно определяется формой Лами С.14).

Уравнение C.14) называется уравнением Крамера 10). Формула Крамера до сих пор была Предположение о существовании решения и доказательство его единственности нос Осталось доказать существование решения системы C.10). Для этого Благодаря Кронекеру — теоремы Капелли достаточно, чтобы доказать ее ранг Основная матрица С.11) равна рангу расширенной матрицы 11) «11 «22 «В 2р «Nl» n2 С.15)

Но это очевидно. Из-за отношения Φ0, основной ранг Матрица n является n, ранг расширенной матрицы, содержащей n строк C.15) Поскольку оно не может превышать число n, оно равно основному рангу Матрица. 9) Чтобы убедиться в этом, достаточно записать разложение детерминанта Aj (pi) элементом в i-м столбце. 10) Габриэль Крамер A704-1752) — швейцарский математик.

• 11) Есть еще один способ доказать существование системного решения мы C.10), который состоит из проверки того, что числа x \, X2, •••, xn определены. Согласно уравнению Крамера C.14), они превращают все уравнения системы C.10) в тождества. Таким образом, линейная квадратная система полностью доказана Формула С.10)

Определитель основной матрицы отлично С нуля, имеет единственное решение, определяемое по форме Мул Крамер C.14). Утверждение, которое мы доказали, еще легче установить По-новому. Для этого замените (как в §1§1) Система C.10) Эквивалентное матричное уравнение AX = B.

Где A — основная матрица системы C.11, X и B — столбцы, С.16) X = X2 В = Людмила Фирмаль

Первый определяется, а второй дается. Поскольку определитель матрицы A не равен нулю, Обратная матрица от A до r (см. Подраздел 7 из 2 в главе 1). Предположим, что решение для системы C.10) существует. Столбец X является тождеством матричного уравнения С.16). Умножьте указанный тождество слева на обратное Рица А

1 A’1 (AX) = A’1 B С.17)

Из-за сочетания характеристик трех продуктов, Матрица (см. Подраздел 2 главы 1 § 1) и соотношение A-1A = E, E Матрица идентичности (см. Раздел 7§2Ch. 1), A (AX) = (от A до rA) X = EX = = X, так что берите из С.17) Х = А до 1В. С.18) Расширяя уравнение C.18), принимая во внимание форму обратной матрицы 12), Получите выражение Крамера для элемента в столбце X.

Следовательно, решение матричного уравнения С.16) имеет вид Если он присутствует, он однозначно определяется соотношением С.18)), Атомная формула Крамера. Легко убедиться, что столбец X определен с помощью: Фактически, C.18) является решением матричного уравнения C.16). 2) гл. См. П. 7 § 2 формулы А.41) 1.

Другими словами, если вы подставите это уравнение, оно превратится в тождество. в Фактически, если столбец X определяется уравнением C.18), AX = = A (от A до 1B) = (AA-> B = EB = B. Следовательно, если определитель D матрицы A отличен от нуля (то есть Существует, если эта матрица невырождена) Единственное решение матричного уравнения С.16) Мои отношения C.18) эквивалентны формуле Крамера.

Пример. Найти решение квадратной системы линейных уравнений коленный xi + 2×2 + Zzh3 + 4zh4 = 30, -xx + 2×2-Зж3 + 4ж4 = 10, % 2-X3 + W4 = 3 X \ + X2 + Xs + X4 = 10 Ненулевой определитель главной матрицы L = 1 -1 0 1 2 2 1 1 3 -3 -1 1 4 4 1 1 = -4. с того времени 30 -1 3 1 10 1 3 4 3 4 -1 1 1 1 = -4, к = Az = 1 2 30 4 №1 2 10 4 0 13 1 1 1 10 1 = -12, L4 = 1 1 0 1 1 1 0 1 30 10 3 10 2 2 1 1 — — 3 -3 -1 1 3 3 1 1 4 4 1 1 30 10 3 10 = -16

Во-вторых, благодаря формуле Крамера, Формат системы: x1-1, x

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Квадратная система линейных уравнений это

Пример 5. Решите уравнение 3у + у 2 = у.
Решение:
3у + у 2 = у – неполное квадратное уравнение; у 2 + 3у – у = 0;
у 2 + 2у =0; у∙(у + 2) = 0.

x 2 – 5х = – 6 или х 2 – 5х = 36;
х 2 – 5х + 6 = 0 или х 2 – 5х – 36 =0.
По теореме Виета:
х₁ = 2, х₂ = 3, х₃ = – 4, х₄ =9.
Ответ: – 4, 2, 3, 9.

Квадратная система линейных уравнений это

Системы линейных уравнений

Линейное уравнение (л.у.) – уравнение вида

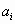
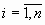
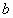
где – числа, называемые коэффициентами л.у., ,

– число, называемое свободным членом л.у.

Система линейных уравнений (СЛУ) – система вида

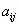
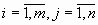
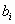
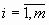
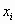
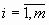
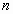
где – числа, называемые коэффициентами СЛУ, ,

– числа, называемые свободными членами СЛУ, ,

– переменные СЛУ, ,

– количество уравнений СЛУ,

– количество переменных СЛУ.

Сокращенная форма записи СЛУ (2)

, .

Матричная форма записи СЛУ (2)

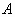
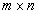
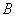
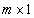
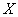
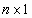
где – матрица коэффициентов СЛУ размерности ,

– вектор свободных членов СЛУ размерности ,

– вектор переменных СЛУ размерности ,

0 – нуль-вектор размерности .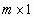

Квадратная СЛУ – СЛУ, состоящая из n уравнений с n переменными.

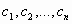
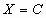
Решение СЛУ с n переменными – упорядоченная совокупность чисел ( для(4)), являющихся решением каждого из уравнений, входящих в систему.

1. Точные методы решения – методы решения, дающие точное решение задачи за конечное число арифметических и логических операций в предположении отсутствия округлений. Применяются для решения задач с малым числом переменных – не более 10 3 .

2. Итеративные методы решения – методы решения, дающие возможность получить решение с заданной точностью или точное решение. Применяются для решения задач со средним числом переменных – не более 10 6 . Требуют меньше вычислений, чем точные методы решения.

3. Вероятностные методы решения. Применяются для решения задач с большим числом переменных – более 10 6 .

Совместная СЛУ – СЛУ, имеющая одно или несколько решений.

Определенная СЛУ – совместная СЛУ, имеющая единственное решение.

Неопределенная СЛУ – совместная СЛУ, имеющая более одного решения.

Несовместная СЛУ – СЛУ, не имеющая ни одного решения.

Однородная СЛУ (ОСЛУ) – СЛУ, все свободные члены которой равны нулю

,

, ,

.

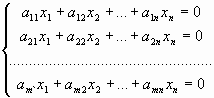
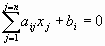
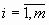
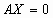
1. Любая ОСЛУ имеет хотя бы одно решение – тривиальное решение, т.е. .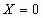

2. Для того чтобы ОСЛУ имела нетривиальные решения, необходимо и достаточно, чтобы ранг матрицы коэффициентов системы был меньше количества переменных системы.

Неоднородная СЛУ (НСЛУ) – СЛУ, у которой хотя бы один свободный член отличен от нуля

.

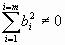
1. Для того чтобы НСЛУ была совместной СЛУ, необходимо и достаточно, чтобы ранг матрицы коэффициентов равен рангу расширенной матрицы (7).

2. Квадратная НСЛУ с вырожденной матрицей коэффициентов может быть совместной неопределенной системой или несовместной системой.

,

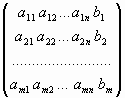
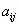
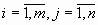
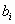
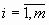
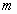
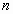
где – коэффициенты СЛУ, ,

– свободные члены СЛУ, ,

– количество уравнений СЛУ,

– количество переменных СЛУ.

Равносильные СЛУ – две СЛУ, множества решений которых совпадают.

1. Всякие две несовместные системы считаются равносильными.

Элементарные преобразования СЛУ :

— умножение некоторого уравнения системы на отличное от нуля число;

— прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число;

— перестановка местами двух уравнений системы;

— перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений.

Эквивалентные СЛУ – две СЛУ, полученные одна из другой с помощью элементарных преобразований.

1. Любые две эквивалентные СЛУ – равносильные.

2. Любая СЛУ приводится посредством элементарных преобразований к системе с трапециевидной матрицей.

3. Любая квадратная СЛУ с невырожденной матрицей коэффициентов A приводится посредством элементарных преобразований к системе с треугольной матрицей.