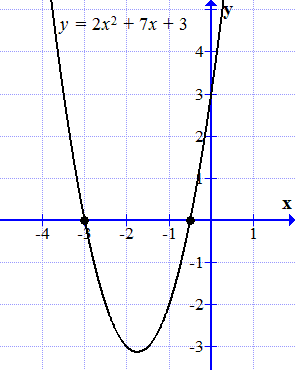Квадратное уравнение и его корни на графике

Квадратичная функция и ее график

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где 0″ title=»a<>0″/> называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.

График функции имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .

Если старший коэффициент a , то ветви параболы напрaвлены вниз .

Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если 0″ title=»a>0″/>,то график функции выглядит как-то так:

2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если 0″ title=»a>0″/>,то график функции выглядит примерно так:

3 . Если 0″ title=»D>0″/>,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

,

Если 0″ title=»a>0″/>,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как 0″ title=»a=2>0″/>,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

0″ title=»D=b^2-4ac=9-4*2*(-5)=49>0″/>

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

,

3. Координаты вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2 . Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы

или в уравнении квадратичной функции , и второй коэффициент — четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

• сначала построить график функции ,
• затем одинаты всех точек графика умножить на 2,
• затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

2. Координаты вершины параболы:

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,

— сдвига графика функции вдоль оси от значения
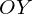
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

И.В. Фельдман, репетитор по математике.

Корни квадратного уравнения

Основные формулы

Рассмотрим квадратное уравнение:
(1) .
Корни квадратного уравнения (1) определяются по формулам:
; .
Эти формулы можно объединить так:
.
Когда корни квадратного уравнения известны, то многочлен второй степени можно представить в виде произведения сомножителей (разложить на множители):
.

Далее считаем, что – действительные числа.
Рассмотрим дискриминант квадратного уравнения:
.
Если дискриминант положителен, , то квадратное уравнение (1) имеет два различных действительных корня:
; .
Тогда разложение квадратного трехчлена на множители имеет вид:
.
Если дискриминант равен нулю, , то квадратное уравнение (1) имеет два кратных (равных) действительных корня:
.
Разложение на множители:
.
Если дискриминант отрицателен, , то квадратное уравнение (1) имеет два комплексно сопряженных корня:
;
.
Здесь – мнимая единица, ;
и – действительная и мнимая части корней:
; .
Тогда

.

Графическая интерпретация

Если построить график функции
,
который является параболой, то точки пересечения графика с осью будут корнями уравнения
.
При , график пересекает ось абсцисс (ось ) в двух точках (см. рисунок ⇓).
При , график касается оси абсцисс в одной точке (см. рисунок ⇓).
При , график не пересекает ось абсцисс (см. рисунок ⇓).

Полезные формулы, связанные с квадратным уравнением

Вывод формулы для корней квадратного уравнения

Выполняем преобразования и применяем формулы (f.1) и (f.3):

,
где
; .

Итак, мы получили формулу для многочлена второй степени в виде:
.
Отсюда видно, что уравнение

выполняется при
и .
То есть и являются корнями квадратного уравнения
.

Примеры определения корней квадратного уравнения

Пример 1

Найти корни квадратного уравнения:
(1.1) .

Запишем квадратное уравнение в общем виде:
.
Сравнивая с нашим уравнением (1.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант положителен, , то уравнение имеет два действительных корня:
;
;
.

Отсюда получаем разложение квадратного трехчлена на множители:

.

График функции y = 2 x 2 + 7 x + 3 пересекает ось абсцисс в двух точках.

Построим график функции
.
График этой функции является параболой. Она пересевает ось абсцисс (ось ) в двух точках:
и .
Эти точки являются корнями исходного уравнения (1.1).

Пример 2

Найти корни квадратного уравнения:
(2.1) .

Запишем квадратное уравнение в общем виде:
.
Сравнивая с исходным уравнением (2.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант равен нулю, , то уравнение имеет два кратных (равных) корня:
;
.

Тогда разложение трехчлена на множители имеет вид:
.

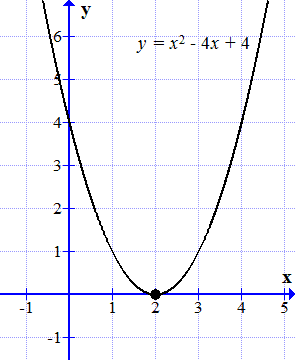
График функции y = x 2 – 4 x + 4 касается оси абсцисс в одной точке.

Построим график функции
.
График этой функции является параболой. Она касается оси абсцисс (ось ) в одной точке:
.
Эта точка является корнем исходного уравнения (2.1). Поскольку этот корень входит в разложение на множители два раза:
,
то такой корень принято называть кратным. То есть считают, что имеется два равных корня:
.

Пример 3

Найти корни квадратного уравнения:
(3.1) .

Запишем квадратное уравнение в общем виде:
(1) .
Перепишем исходное уравнение (3.1):
.
Сравнивая с (1), находим значения коэффициентов:
.
Находим дискриминант:
.
Дискриминант отрицателен, . Поэтому действительных корней нет.

Можно найти комплексные корни:
;
;
.

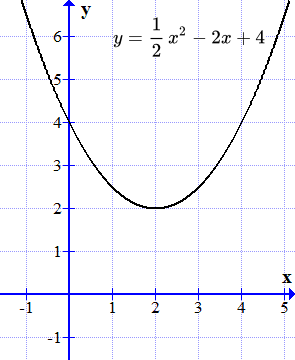
График функции не пересекает ось абсцисс. Действительных корней нет.

Построим график функции
.
График этой функции является параболой. Она не пересекает ось абсцисс (ось ). Поэтому действительных корней нет.

Действительных корней нет. Корни комплексные:
;
;
.

Автор: Олег Одинцов . Опубликовано: 19-04-2016

Решение квадратных уравнений

Квадратное уравнение – это математическое уравнение, которое в общем виде выглядит так:

Это многочлен второго порядка с 3 коэффициентами:

• a – старший (первый) коэф., не должен быть равен 0;
• b – средний (второй) коэф.;
• c – свободный элемент.

Решением квадратного уравнения является нахождение двух чисел (его корней) – x₁ и x₂.

Формула для вычисления корней

Для нахождения корней квадратного уравнения используется формула:

Выражение внутри квадратного корня называется дискриминантом и обозначается буквой D (или Δ):

Таким образом, формула для вычисления корней может быть представлена разными способами:

1. Если D > 0, у уравнения есть 2 корня:

2. Если D = 0, уравнение имеет всего один корень:

3. Если D Решений квадратных уравнений

Пример 1

Решение:

Пример 2

Решение:

Пример 3

Решение:

В данном случае нет вещественных корней, а решением являются комплексные числа:

График квадратичной функции

Графиком квадратичной функции является парабола.

• Корни квадратного уравнения – это точки пересечения параболы с осью абцисс (X).
• Если корень один – парабола касается оси в одной точке, не пересекая ее.
• При отсутствии вещественных корней (наличии комплексных), график с осю X не соприкасается.