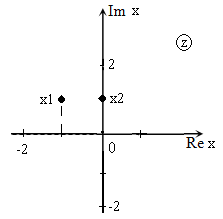Квадратное уравнение с комплексными корнями
Вы будете перенаправлены на Автор24
Рассмотрим решение уравнений с комплексными корнями и коэффициентами.
Двучленным называется уравнение вида $x^
Рассмотрим три случая:
Решить уравнение: $x^ <3>=8$.
Так как $A>0$, то $x_
При $k=0$ получаем $x_ <0>=\sqrt[<3>] <8>\cdot \left(\cos 0+i\cdot \sin 0\right)=\sqrt[<3>] <8>=2$.
При $k=1$ получаем
\[x_ <1>=\sqrt[<3>] <8>\cdot \left(\cos \frac<2\pi > <3>+i\cdot \sin \frac<2\pi > <3>\right)=\sqrt[<3>] <8>\cdot (-\frac<1> <2>+\frac <\sqrt<3>> <2>\cdot i)=2\cdot (-\frac<1> <2>+\frac <\sqrt<3>> <2>\cdot i)=-1+\sqrt <3>\cdot i.\]
При $k=2$ получаем
\[x_ <2>=\sqrt[<3>] <8>\cdot \left(\cos \frac<4\pi > <3>+i\cdot \sin \frac<4\pi > <3>\right)=\sqrt[<3>] <8>\cdot (-\frac<1> <2>-\frac <\sqrt<3>> <2>\cdot i)=2\cdot (-\frac<1> <2>-\frac <\sqrt<3>> <2>\cdot i)=-1-\sqrt <3>\cdot i.\]
Решить уравнение: $x^ <3>=1+i$.
Готовые работы на аналогичную тему
Так как $A$ — комплексное число, то
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.
По условию $a=1,b=1$.
Вычислим модуль исходного комплексного числа:
Вычислим аргумент исходного комплексного числа:
\[\varphi =\arg z=arctg\frac<1> <1>=arctg1=\frac<\pi > <4>\]
Подставим полученные значения и получим:
Уравнение перепишем в виде:
При $k=0$ получаем $x_ <0>=\sqrt[<3>] <\sqrt<2>> \cdot \left(\cos \frac<\pi /4> <3>+i\cdot \sin \frac<\pi /4> <3>\right)=\sqrt[<3>] <\sqrt<2>> \cdot \left(\cos \frac<\pi > <12>+i\cdot \sin \frac<\pi > <12>\right)=\sqrt[<6>] <2>\cdot \left(\cos \frac<\pi > <12>+i\cdot \sin \frac<\pi > <12>\right)$.
При $k=1$ получаем
При $k=2$ получаем
Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.
Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом
В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.
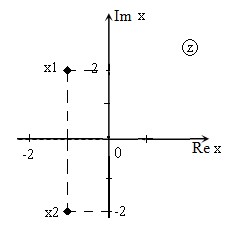
Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.
\[D=2^ <2>-4\cdot 1\cdot 5=4-20=-16.\]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.
В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.
Комплексное число вида $\overline
Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.
Зная корни уравнения $x_ <1,2>=1\pm 2i$, записать исходное уравнение.
Запишем уравнение следующим образом:
\[x^ <2>-(1-2i)\cdot x-x\cdot (1+2i)+(1-2i)\cdot (1+2i)=0\] \[x^ <2>-x+2i\cdot x-x-2i\cdot x+1-4i^ <2>=0\] \[x^ <2>-2x+1+4=0\] \[x^ <2>-2x+5=0\]
Следовательно, $x^ <2>-2x+5=0$ — искомое уравнение.
Рассмотрим квадратное уравнение с комплексными коэффициентами.
Решить уравнение: $z^ <2>+(1-2i)\cdot z-(1+i)=0$ и изобразить корни на плоскости.
Так как $D>0$, уравнение имеет два корня:
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 13 11 2021
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Работаем по будням с 10:00 до 20:00 по Мск
. и многие другие.
Успешной учебы! Будем рады вам помочь!
Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
Рассматривать будем на таком примере:
Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:
Выполним проверку того, что эти корни и права оказываются решением уравнения:
Что и требовалось доказать.
Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: 
Такие корни являются сопряженными комплексными корнями.
Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:




В каждом случае получаем 2 сопряженных комплексных корня.
Решим квадратное уравнение 
Первым шагом определим дискриминант уравнения:
В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:
Как известно из формул дискриминанта у нас образуется 2 корня:

Т.о., у уравнения 

Теперь можно решить любое квадратное уравнение!
У любого уравнения с многочленом n-ой степени 
Как извлечь корень из произвольного комплексного числа?
Рассмотрим уравнение z n = w, либо, записав в другом виде: 
В частности, при n = 2 получаем квадратный корень 
У уравнения типа 

где 
φ – его аргумент,
а параметр k принимает значения: 
Найдем корни уравнения: 
Перепишем уравнение как: 
В этом примере 



Далее найдем модуль и аргумент комплексного числа 
Число w находится в 1-ой четверти, значит:
Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.
Детализируем еще немного общую формулу:


Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.
Подставляем в формулу значение k = 0 и получаем 1-й корень:

Подставляем в формулу значение k = 1 и получаем 2-й корень:

Ответ: 
Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.
Часто вычисленные корни нужно изобразить геометрически:
Как выполнить чертеж?
Для начала на калькуляторе вычисляем, чему равен модуль корней 
Далее берем аргумент 1-го корня 

Отмеряем транспортиром 45° и ставим на чертеже точку z0.
Берем аргумент 2-го корня 

По этому же алгоритму ставим точку z2.
Видно, что корни располагаются геометрически правильно с интервалом 
Квадратное уравнение с комплексными корнями — справочник студента
Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.
Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:
Пример 1. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа
Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.
Пример 2. Найти все корни уравнения
Найдем дискриминант уравнения:

- Найдем корни уравнения:
- Ответ:
- Пример 3. Найти все корни уравнения
- Выразим z из уравнения:
- Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа
Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = <0, 1, 2, 3>. Найдем модуль комплексного числа:
- Подставим найденные значения в формулу:
- Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:
- Ответ:
- Пример 4. Найти корни уравнения
- Решение кубического уравнения комплексными числами:
- Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.
- Найдем все необходимые значения для формулы:
- Подставим найденные значения в формулу:
- Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:
- Ответ:
- Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.
Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.
После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.
Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.
Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.
Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.
Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.
Решение кубических уравнений. Формула Кардано
| Справочник по математике | Алгебра | Кубические уравнения |
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени (кубических уравнений)
| a0x3 + a1x2 ++ a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа,
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями.
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x3 + ax2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
то уравнение (2) примет вид
В результате уравнение (2) примет вид
  | (4) |
Если ввести обозначения
- то уравнение (4) примет вид
- где p, q – вещественные числа.
- Уравнения вида (5) и являются трёхчленными кубическими уравнениями, у которых отсутствует член со второй степенью неизвестного.
- Первый этап вывода формулы Кардано завершён.
Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
 | (6) |
где t – новая переменная.
то выполнено равенство:
Следовательно, уравнение (5) переписывается в виде
Если теперь уравнение (7) умножить на t, то мы получим квадратное уравнение относительно t :
Формула Кардано
Решение уравнения (8) имеет вид:
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
В развернутой форме эти решения записываются так:
| (10) |
| (11) |
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
С другой стороны,
- Таким образом,
- и для решения уравнения (5) мы получили формулу
| (12) |
которая и называется «Формула Кардано».
Замечание. Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Пример решения кубического уравнения
Пример. Решить уравнение
| x3 – 6×2 – 6x – 2 = 0. | (13) |
Решение. Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
- Тогда получим
- x3 – 6×2 – 6x – 2 == (y + 2)3– 6(y + 2)2 –– 6(y + 2) – 2 == y3 + 6y2 + 12y + 8 – 6y2 –– 24y – 24 – 6y – 12 – 2 == y3 – 18y – 30.
- Следовательно, уравнение (13) принимает вид
- Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
| (16) |
то уравнение (15) примет вид
Далее из (17) получаем:
Отсюда по формуле (16) получаем:
| (18) |
- Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
- или использовали формулу
- Далее из равенства (18) в соответствии с (14) получаем:
- Таким образом, мы нашли у уравнения (13) вещественный корень
Замечание 1. У уравнения (13) других вещественных корней нет.
Замечание 2. Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня.
Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел.
Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Корни квадратного уравнения
Формулы корней квадратного уравнения. Рассмотрены случаи действительных, кратных и комплексных корней. Разложение на множители квадратного трехчлена. Геометрическая интерпретация. Примеры определения корней и разложения на множители.
Основные формулы ⇓Графическая интерпретация ⇓Полезные формулы, связанные с квадратным уравнением ⇓Вывод формулы для корней квадратного уравнения ⇓Примеры определения корней квадратного уравнения ⇓ Пример 1 ⇓ Пример 2 ⇓ Пример 3 ⇓
Рассмотрим квадратное уравнение: (1) . Корни квадратного уравнения (1) определяются по формулам: ; . Эти формулы можно объединить так:
Когда корни квадратного уравнения известны, то многочлен второй степени можно представить в виде произведения сомножителей (разложить на множители):
Далее считаем, что – действительные числа. Рассмотрим дискриминант квадратного уравнения: . Если дискриминант положителен, , то квадратное уравнение (1) имеет два различных действительных корня: ; . Тогда разложение квадратного трехчлена на множители имеет вид:
Если дискриминант равен нулю, , то квадратное уравнение (1) имеет два кратных (равных) действительных корня: . Разложение на множители:
Если дискриминант отрицателен, , то квадратное уравнение (1) имеет два комплексно сопряженных корня: ; . Здесь – мнимая единица, ; и – действительная и мнимая части корней: ; . Тогда .
Графическая интерпретация
Если построить график функции , который является параболой, то точки пересечения графика с осью будут корнями уравнения . При , график пересекает ось абсцисс (ось ) в двух точках (см. рисунок ⇓). При , график касается оси абсцисс в одной точке (см. рисунок ⇓). При , график не пересекает ось абсцисс (см. рисунок ⇓).
Полезные формулы, связанные с квадратным уравнением
Вывод формулы для корней квадратного уравнения
Выполняем преобразования и применяем формулы (f.1) и (f.3): , где
- ; .
- Итак, мы получили формулу для многочлена второй степени в виде: . Отсюда видно, что уравнение выполняется при
- и .
То есть и являются корнями квадратного уравнения .
Примеры определения корней квадратного уравнения
Пример 1
Найти корни квадратного уравнения: (1.1) .
Запишем квадратное уравнение в общем виде: . Сравнивая с нашим уравнением (1.1), находим значения коэффициентов:
Поскольку дискриминант положителен, , то уравнение имеет два действительных корня: ; ; .
Отсюда получаем разложение квадратного трехчлена на множители: .

Построим график функции . График этой функции является параболой. Она пересевает ось абсцисс (ось ) в двух точках: и . Эти точки являются корнями исходного уравнения (1.1).
Пример 2
Найти корни квадратного уравнения: (2.1) .
Запишем квадратное уравнение в общем виде: . Сравнивая с исходным уравнением (2.1), находим значения коэффициентов:
Поскольку дискриминант равен нулю, , то уравнение имеет два кратных (равных) корня: ; .
Тогда разложение трехчлена на множители имеет вид: .

Построим график функции . График этой функции является параболой. Она касается оси абсцисс (ось ) в одной точке: . Эта точка является корнем исходного уравнения (2.1). Поскольку этот корень входит в разложение на множители два раза:
то такой корень принято называть кратным. То есть считают, что имеется два равных корня:
Пример 3
Найти корни квадратного уравнения: (3.1) .
Запишем квадратное уравнение в общем виде: (1) . Перепишем исходное уравнение (3.1):
Сравнивая с (1), находим значения коэффициентов: Находим дискриминант: Дискриминант отрицателен, . Поэтому действительных корней нет.
- Можно найти комплексные корни: ; ; .
- Тогда .

Построим график функции . График этой функции является параболой. Она не пересекает ось абсцисс (ось ). Поэтому действительных корней нет.
Действительных корней нет. Корни комплексные: ; ; .
Квадратное уравнение
— это уравнение вида a x2 + b x + c = 0, где a не равно 0.
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют точки пересечения параболы с осью абсцисс.
Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней.
Если парабола пересекается с осью абсцисс в одной точке (вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня.
Если коэффициент a положительный, ветви параболы направлены вверх, если отрицательный — ветви параболы направлены вниз. Если коэффициент b положительный, то вершина параболы лежит в левой полуплоскости, если отрицательный — в правой полуплоскости.
Вывод формулы для решения квадратного уравнения
Формулу для решения квадратного уравнения a x2 + b x + c = 0 можно получить так:
- перенесем c в правую часть a x2 + b x = — c
- умножим уравнение на 4a (2a x)2 + 4a b x = — 4a c
- добавим b2 к обоим частям (2a x)2 + 4a b x + b2 = b2 — 4a c
- в левой части выделим полный квадрат (2a x + b)2 = b2 — 4a c
- извлечем квадратный корень 2a x + b = ± √b2 — 4a c
- перенесем b в правую часть 2a x = — b ± √b2 — 4a c
- разделим уравнение на 2a
квадратного уравнения называют число равное D = b2 − 4ac
Квадратное уравнение с вещественными коэффициентами может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта:
- при D > 0 корней два, и они вычисляются по формуле
- при D = 0 корень один (два равных или совпадающих корня), кратности 2:
- при D https://ru.onlinemschool.com/math/library/equation_quadratic/
Квадратное уравнение с комплексными коэффициентами
| Вы ввели следующее выражение |
| Результат решения заданного уравнения |
- Как известно, квадратное уравнение: имеет корни, которые вычисляются по простой форумуле .
- Онлайн решений очень много, наш же бот, вычисляет квадратное уравнение, если его коэффициенты являются комплексными числами.
- В русскоязычном секторе Интернета, такого сервиса нет, и наш бот будет тут первым.
Хотелось бы заметить, что коэффициентами квадратного уравнения могут быть не только комплексные числовые значения, но и произвольное комплексное выражение. Это несомненно расширяет возможности представленного сервиса, и дает определенные преимущества.
Ну и естественно, для тех кто хорошо учился в школе, и понимающих, что комплексные числа это лишь расширенное представление наших «обычных» действительных чисел, следует вывод, что данный сервис правильно считает и в том случае, если числа в коэффициентах имеют действительные значения.
Для того, что бы по известным корням можно было построить произвольное уравнение, в том числе и квадратное с комплексными коэфициентами можно воспользоватся ресурсом Создание полинома (многочлена) одной переменной онлайн
Синтаксис
- Для всех кто пользуется XMPP клиентами: ur2_i
- Коэффициенты уравнения могут быть как действительными так и мнимыми значениями.
Примеры
- Пишем в поле ввода коэффициенты
- 4 8-i -i
- Не забудьте, что как минимум одним пробелом разделяются эти значения
- ответ будет следующий
| Вы ввели следующее выражение |
| Результат решения заданного уравнения |
| Решаем комплексное уравнение: x^2 + (2-0.25i)*x + (0-0.25i)= 0 Первый корень уравнения = -0.0078432583508+0.125i Второй корень уравнения = -1.9921567416492+0.125i |
Давайте проверим, а правильно ли нам посчитал бот эти корни. Для этого воспользуемся Аргумент и значения функции комплексной переменной и посчитаем чему же будет равно значение функции, при полученных корнях
При выборе первого корня ответ будет такой:
| Вы ввели следующую функицю | ||||
| Табличное представление значений функции | ||||
|
Несмотря на небольшую погрешность, результат говорит нам о том что расчеты проведены верно
- Здесь мы видим, что коэффициенты представлены в виде комплексных выражений, но для бота это не помеха.
- пишем в запросе
- 2-i ln(1+sin(i)) -3
- и получаем результат
| Вы ввели следующее выражение |
| Результат решения заданного уравнения |
| Решаем комплексное уравнение: x^2 + (0.0003584355453+0.4330639593925i)*x + (-1.2-0.6i)= 0 Первый корень уравнения = 1.1073006922543+0.0543883355731i Второй корень уравнения = -1.1076591277997-0.4874522949657i |
Удачи в расчетах!
Лекция 4. КОМПЛЕКСНЫЕ ЧИСЛА
Г. Глейзер, Москва
Формула Муавра и корни из единицы
Правило умножения двух комплексных чисел позволяет получить замечательное соотношение, открытое английским математиком А. де-Муавром (1667–1754).
Найдем квадрат комплексного числа z = r(cos j + i sin j), т.е. результат произведения этого числа на само себя:
- z2 = z•z = r(cos j + i sin j)•r(cos j + i sin j).
- По правилу умножения двух комплексных чисел имеем: z2 = r2(cos j + i sin j)2 = r2(cos 2j + i sin 2j).
- Повторяя n раз операцию возведения в степень числа z, мы получим формулу n-ой степени числа z:
- zn = rn(cos nj + i sin nj),
- где n – натуральное число.
Методом математической индукции можно доказать эту формулу. Она представляет собой обобщение формулы, открытой Муавром. Муавр открыл ее для случая, когда модуль комплексного числа z равен 1. Формула Муавра имеет вид:
- (cos j + i sin j)n = cos nj + i sin nj,
- где n О N.
- С помощью формулы Муавра можно вывести многие полезные соотношения, в частности, между тригонометрическими выражениями.
Формула Муавра позволяет найти значения корней любой (n-й) степени в поле комплексных чисел. Под корнем n-й степени из числа z понимают такое число a, n-я степень которого равна z: an = z. Ограничимся рассмотрением вопроса об извлечении корня n-ой степени из 1 в поле комплексных чисел.
Другими словами, будем рассматривать вопрос о решении уравнения zn = 1, где n О N в поле комплексных чисел. Например, корень квадратный из числа 1 имеет два значения: 1 и – 1. Действительно, 12 = 1 и (– 1)2 = 1. Корень четвертой степени из числа 1 в поле комплексных чисел имеет четыре значения: два действительных, 1 и – 1, и два мнимых, i и – i.
Этот факт можно установить проверкой: 14 = 1 и (– 1)4 = 1; i4 = 1 и (– i)4 = 1.
Эти два примера наводят на предположение о том, что корень кубический из 1 в поле комплексных чисел должен иметь 3 значения; корень пятой степени из 1 должен иметь пять значений и т.д. Корень n-й степени из числа 1 в поле комплексных чисел должен иметь n значений.
Это предположение оказывается верным. Воспользовавшись формулой Муавра, можно доказать, что уравнение zn = 1 в поле комплексных чисел имеет ровно n решений, т. е.
корень n-й степени из числа z в поле комплексных чисел имеет ровно n значений.
Эти значения корня изображаются вершинами правильного n-угольника, вписанного в единичную окружность, причем точка (0; 1) является одной из вершин этого многоугольника.
Итак, первый корень уравнения zn = 1 изображается вершиной вписанного n-угольника, т. е.
Второй корень изображается следующей вершиной вписанного n-угольника т. е.
Аналогично могут быть найдены другие корни:
Наконец, последний n-й корень будет как раз изображаться точкой (0; 1):
На рисунке 11 изображены корни уравнения z3 = 1, т.е. значения кубического корня из 1 в поле комплексных чисел. Эти значения получены следующим образом:
На рисунке 12 изображены корни уравнения z4 =1, т.е. значения корня четвертой степени из 1 в поле комплексных чисел. Эти значения получены следующим образом:
Рис. 12
На рисунке 13 изображены корни уравнения z6 =1, т. е. значения корня шестой степени из 1 в поле комплексных чисел. Эти значения получены следующим образом:
На рисунке 14 изображены корни уравнения z12 = 1, т.е. значения корня двенадцатой степени из 1 в поле комплексных чисел (вычисления этих значений не приводим).
Основная теорема алгебры
Изученные сведения о комплексных числах позволяют рассмотреть вопрос о решении алгебраических уравнений в поле комплексных чисел. Напомним, что алгебраическим уравнением называют уравнение вида:
anxn + an–1xn–1 + an–2xn–2 + … + a1x + a0 = 0.
Левая часть его представляет собой некоторый многочлен f(x), где x – неизвестное, an, an–1, an–2, … a1, a0 – коэффициенты (действительные или комплексные числа), n – натуральное число. Если an № 0, то мы имеем дело с уравнением n-ой степени, т.е. степень уравнения совпадает с высшей степенью неизвестного.
Корнем (или решением) уравнения f(x) = 0 называется такое число t, при подстановке которого вместо неизвестного в данное уравнение мы получаем верное числовое равенство: f(x) = 0.
Нам известно, что каждое уравнение первой степени ax + b = 0 (a № 0) имеет решение Нам также известно, что каждое квадратное уравнение ax2 + bx + c = 0 имеет два решения:
где D = b2 – 4ac – дискриминант квадратного уравнения. Правда, если D = 0, то эти решения совпадают.
Выше было установлено, что уравнение вида xn – 1 = 0 также имеет решения, более того, таких решений ровно столько, какова степень этого уравнения.
В связи с этим можно поставить вопросы: всякое ли алгебраическое уравнение имеет решение в поле комплексных чисел? Ответ на этот вопрос имеет длительную и богатую историю (смотри ниже историческую справку).
В 1799 г. тогда еще молодому немецкому математику Гауссу удалось доказать важную теорему о том, что решения алгебраических уравнений 5-й и более высоких степеней существуют. В теореме Гаусса утверждается, что всякое алгебраическое уравнение с действительными и даже комплексными коэффициентами имеет по крайней мере один комплексный корень.
Приведенная выше теорема Гаусса позволила завершить изучение принципиально важного вопроса о разрешимости алгебраических уравнений и доказать основную теорему алгебры, смысл которой состоит в том, что всякий многочлен n-й степени (см. левую часть уравнения) может быть разложен на n линейных множителей, откуда непосредственно следует, что всякое алгебраическое уравнение n-й степени имеет, вообще говоря, n корней.
Доказательство этой теоремы (способов такого доказательства существует несколько) выходит за рамки данного курса. Отметим лишь, что почти все они базируются на геометрической интерпретации комплексных величин на плоскости.
Поясним смысл этой теоремы на отдельных примерах. Рассмотрим уравнение x4 – 4 = 0. Левая часть этого уравнения – многочлен f(x)=x4 – 1. Основная теорема алгебры утверждает, что этот многочлен может быть разложен на 4 линейных множителя, именно
f(x) = (x + 1)(x – 1)(x + i)(x – i).
Подставим полученное разложение в данное уравнение: (x + 1)(x – 1)(x + i)(x – i) = 0. Теперь, приравнивая к нулю каждый из сомножителей, получим четыре корня данного уравнения:
x + 1 = 0, x1 = – 1; x – 1 = 0, x2 = 1; x + i = 0, x3 = – i; x – i = 0, x4 = i.
Таким образом, данное уравнение имеет четыре корня, ровно столько, какова его степень.
Рассмотрим еще один пример. Рассмотрим квадратное уравнение x2 – 4x + 4 = 0. Левая часть этого уравнения – многочлен f(x) = x2 – 4x + 4, согласно основной теоремы алгебры разлагается на два линейных множителя f(x) = (x – 2)(x – 2).
Эти множители одинаковы, поэтому данное уравнение имеет равные корни x1 = x2 = 2 или только один корень x = 2, рассматриваемый дважды; математики говорят: корень «кратности 2».
И в этом случае число корней алгебраического уравнения совпадает, вообще говоря, с его степенью.
Заметим еще, что введение комплексных чисел позволило в алгебре установить основную теорему в общей форме, не допускающей никаких исключений. Если бы мы ограничивались лишь действительными числами, мы бы могли утверждать только то, что алгебраическое уравнение n-й степени имеет либо n корней, либо меньше, либо не имеет их вовсе.
Историческая справка
Комплексные числа, как впрочем и отрицательные, возникли из внутренней потребности самой математики, конкретнее – из практики и теории решения алгебраических уравнений.
С комплексными числами впервые математики встретились при решении квадратных уравнений.
Вплоть до ХVI века математики всего мира, не находя приемлемого толкования для комплексных корней, возникавших при решении квадратных уравнений, объявляли их ложными и не принимали во внимание.
История решения квадратных уравнений берет свое начало еще из Древнего Вавилона. Вавилоняне умели решать отдельные виды квадратных уравнений 2000 лет до н.э., правда, они находили только положительные корни и не владели общими методами решений. Индус Брахмагупта (VII в.
) изложил общее правило решения квадратного уравнения. Аль-Хорезми (IX в.) дал классификацию линейных и квадратных уравнений и привел способы их решений, правда, и он (как, впрочем, и все математики вплоть до XVII века) не принимал во внимание нулевые и отрицательные решения.
Вывод формул решения квадратных уравнений в общем виде привел Виет (XVI в.). Однако и он признавал только положительные решения. Только в ХVI веке итальянские математики Тарталья, Кардано, Бомбелли учитывают, помимо положительных, отрицательные решения квадратных уравнений.
Лишь в XVII веке, благодаря работам Жирара, Декарта, Ньютона и других математиков, решение квадратных уравнений приобретает современный вид.
Разрешимость уравнений 3-й и 4-й степеней была установлена названными выше итальянскими математиками Тарталья, Кардано и др., причем было установлено, что корни уравнений 3-й и 4-й степеней могут быть найдены с помощью формул, подобных формулам корней квадратных уравнений, но более сложных.
Настойчивые поиски в течение почти двух столетий подобных формул для уравнений 5-й и более высоких степеней не увенчались успехом.
Только в 20-х годах ХIX века молодой норвежский математик Нильс Абель доказал, что иррациональные корни алгебраических уравнений степени выше 4-й не могут быть выражены в виде формул, содержащих только пять операций – четырех арифметических и извлечения корней.
Кардано, занимавшийся решением уравнений 3-й и 4-й степеней (о чем речь шла выше), был одним из первых математиков, формально оперировавших комплексными числами, хотя их смысл во многом оставался для него неясным. Смысл комплексных чисел разъяснил другой итальянский математик Р.Бомбелли. В своей книге «Алгебра» (1572 г.
) он впервые изложил правила действий над комплексными числами в современной форме. Большое внимание комплексным числам уделял А.Жирар, автор замечательного произведения «Новое изобретение в алгебре» (1629 г.). Именно А.Жирар впервые сформулировал основную теорему алгебры, впоследствии доказанную Гауссом.
Вместе с тем, вплоть до XVIII века, комплексные числа считали «воображаемыми» и бесполезными.
Интересно отметить, что даже такой выдающийся математик как Декарт, отождествлявший действительные числа с отрезками числовой прямой, считал, что для комплексных чисел не может быть никакого реального истолкования, и они навечно останутся воображаемыми, мнимыми. Аналогичных взглядов придерживались великие Ньютон и Лейбниц.
Лишь в XVIII веке многие задачи математического анализа, геометрии, механики требовали широкого применения операций над комплексными числами, что создало условия для разработки их геометрического истолкования.
Выдающаяся роль в развитии теории комплексных чисел, разработке методов их применения в различных областях математики принадлежит ряду известных математиков.
В прикладных работах Даламбера и Эйлера в середине XVIII века авторы представляют произвольные мнимые величины в виде a + bi, что позволяет изображать такие величины точками координатной плоскости.
Именно эта интерпретация была использована Гауссом в работе, посвященной исследованию решений алгебраического уравнения. Позднее, в начале ХIХ века в работах К.Весселя и Ж.Аргана содержится полное геометрическое построение комплексных чисел.
В частности, Весселем комплексные числа рассматривались как векторы. Благодаря Коши в математике активно стали использоваться такие понятия, как модуль комплексного числа, сопряженные комплексные числа.
И только в начале XIX века, когда уже была выяснена роль комплексных чисел в различных областях математики, была разработана очень простая и естественная их геометрическая интерпретация, позволившая уяснить геометрический смысл операций над комплексными числами. Этому математика обязана Гауссу, опубликовавшему в 1831 г. свою работу по теории чисел. Тем самым был положен конец сомнениям в законном и полезном применении комплексного числа.
Вопросы для коллективного обсуждения
1. Какие причины вызвали необходимость расширения множества действительных чисел до множества комплексных чисел?
2. В чем состоит общий принцип расширения числовых множеств?
3. Определите комплексное число. Приведите классификацию комплексных чисел.
4. Приведите определения операций сложения и умножения комплексных чисел. Основываясь на этих определениях, покажите справедливость для комплексных чисел коммутативного, ассоциативного и дистрибутивного законов.
5. Какие комплексные числа называют сопряженными? Чему равно произведение комплексных чисел?
6. Покажите на примере как выполняется деление комплексных чисел.
а) in = 1, если n делится на 4; б) in = i, если при делении n на 4 в остатке получаем 1; в) in = – 1, если при делении n на 4 в остатке получаем 2; г) in = – i, если при делении n на 4 в остатке получаем 3.
8. Докажите, что квадратное уравнение с действительными коэффициентами может иметь комплексный корень, причем если такой существует, то и сопряженное комплексное число также корень этого уравнения.
9. Расскажите о геометрической интерпретации комплексных чисел точками координатной плоскости.
10. Расскажите о геометрической интерпретации комплексных чисел с помощью векторов.
11. Дайте определение модуля и аргумента комплексного числа.
12. Расскажите о тригонометрической форме комплексного числа. Как записать в тригонометрической форме комплексное число, заданное в алгебраической форме. Запишите в тригонометрической форме комплексные числа:
а) i; б) – i; в) 1 + i; г) – 1 – i.
13. Покажите, что умножение комплексных чисел связано с поворотом (вращением).
14. Приведите формулу Муавра и проиллюстрируйте ее применение к нахождению корней из единицы. Найдите корни 3-й степени из единицы и проиллюстрируйте их геометрически.
15. Покажите, что квадратный корень из любого комплексного числа существует и имеет два значения.
16. Приведите определение алгебраического уравнения n-й степени и его решения. Сформулируйте основную теорему алгебры.
Упражнения для самостоятельного решения
1. Восполните операции:
а) (3 – 2i) + (4 + 5i); б) (4 – i) – (2 + 3i);
2. Докажите, что xy = yx, для любых комплексных x и y.
3. Докажите, что сумма и произведение двух комплексных сопряженных чисел есть числа действительные.
4. Докажите, что числа – 1 + 3i и – 1 – 3i являются корнями квадратного уравнения x2 + 2x + 10.
5. Представьте в тригонометрической форме числа:
а) 1 – i; б) – 1 – i; в) – 1 + i; г) 1 + i.
6. Найдите корни 6-й степени из единицы и проиллюстрируйте их геометрически.
7. Найдите результат возведения комплексного числа в степень: (1 + i)11.
8. Докажите, что комплексное число равно нулю тогда и только тогда, когда модуль его равен нулю.
9. Докажите, что | xy | = | x |•| y |, где x и y – произвольные комплексные числа.
10. В каких случаях имеет место равенство | x + y | = = | x | + | y |, где x и y – комплексные числа?
Темы для рефератов
1. История происхождения и развития понятия комплексного числа. Литература. Г.И.Глейзер. История математики в средней школе. – М.: Просвещение, 1970.
2. Задание геометрических преобразований комплексными числами. Литература (см. п. 3).
3. Комплексные числа и конформные отображения. Литература. А.И.Маркушевич. Комплексные числа и конформные отображения. – М.: Физматгиз.1960.
4. Развитие понятия числа. Литература. Г. Фройденталь. «Математика как педагогическая задача», ч. 2. – М.: Просвещение, 1982.
5. Кватернионы. Литература: Энциклопедия элементарной математики. Т.1. – М: 1951 Ф. Клейн. Элементарная математика с точки зрения высшей, т. 1. – М.: Наука, 1987.
Комплексные числа и квадратные уравнения. -решение квадратных уравнений на множестве комплексных чисел; -алгоритм извлечения квадратного корня из комплексного. — презентация
1 Комплексные числа и квадратные уравнения. -решение квадратных уравнений на множестве комплексных чисел; -алгоритм извлечения квадратного корня из комплексного числа; -полезные следствия для формулы корней квадратного уравнения Учитель математики МОУ СОШ 2 Чернышова Ирина Сергеевна
2 Квадратное уравнение с действительными коэффициентами ?
3 На множестве С можно находить корни любых квадратных уравнений! Как извлечь квадратный корень из отрицательных действительных чисел? Решение квадратных уравнений с действительными коэффициентами и D
4 Как извлечь квадратный корень из отрицательных действительных чисел? Определение: квадратным корнем(корнем второй степени) из комплексного числа z называют комплексное число, квадрат которого равен z.
5 Формула извлечения квадратного корня из отрицательных действительных чисел
6 Решение квадратных уравнений с действительными коэффициентами и D
7 Как извлечь квадратный корень из любого комплексного числа? (в алгебраической и тригонометрической форме записи). Теорема: Если b0, то Что равносильно системе условий:
9 Избежать громоздких вычислений позволяет тригонометрическая форма записи комплексного числа. Теорема: Теорема: Доказательство: Доказательство: Всегда 2 корня!
10 == = Аналогично: Важно запомнить! При возведении комплексного числа в квадрат – его аргумент удваивается.
11 Алгоритм извлечения квадратного корня из комплексного числа: 1)Найти модуль ρ и аргумент α этого числа; 2)Провести окружность радиусом ρ с центром в начале координат; 3)Провести через начало координат прямую под углом к положительному направлению оси абсцисс; 4)Две точки пересечения проведённых окружности и прямой – дают ответ.
- 13 Решение квадратных уравнений с комплексными коэффициентами. Так как множества и совпадают между собой, то для решения квадратных уравнений с комплексными коэффициентами можно сохранить привычную формулу корней квадратного уравнения:
- 14 Полезные следствия для формулы корней квадратного уравнения: (теорема Виета) Если Z 1 и Z 2 –корни квадратного уравнения то (формула разложения квадратного трёхчлена на линейные множители) Если Z 1 и Z 2 –корни квадратного уравнения то
- 15 Домашнее задание: §35 изучить
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения
Кубическим уравнением называется уравнение вида
- ax3 + bx2 + cx +d = 0 , (1)
- где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Δ= -4b3d + b2c2 — 4ac3 + 18abcd — 27a2d2 (Да, это дискриминант кубического уравнения)
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ 0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
Если Q0, то вычисляем
И наше уравнение имеет 3 корня (вещественных):
- x1= — 2(Q)1/2cos(φ) — a/3
- x2= — 2(Q)1/2cos(φ+2π/3) — a/3
- x3= — 2(Q)1/2cos(φ-2π/3) — a/3
http://www.calc.ru/Chisla-Izvlecheniye-Korney-Iz-Kompleksnykh-Chisel-Kvadratnoy.html
http://school16rostov.ru/estestvennye/kvadratnoe-uravnenie-s-kompleksnymi-kornyami-spravochnik-studenta.html