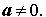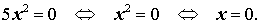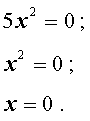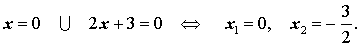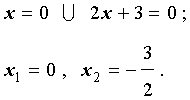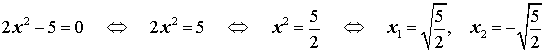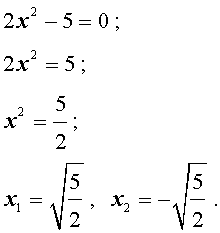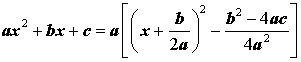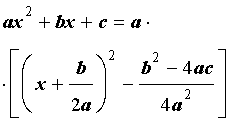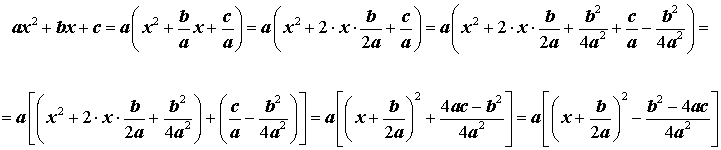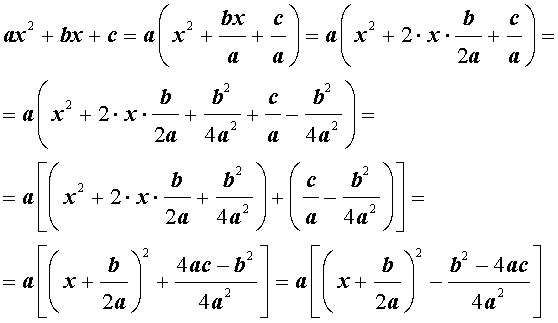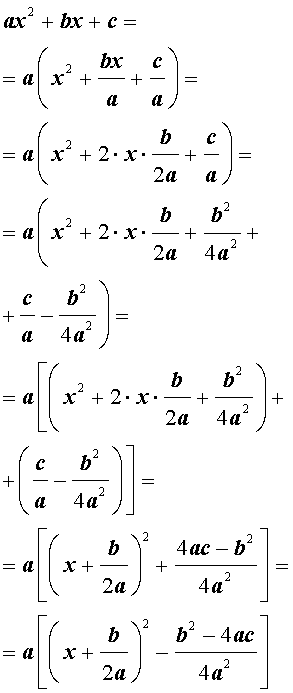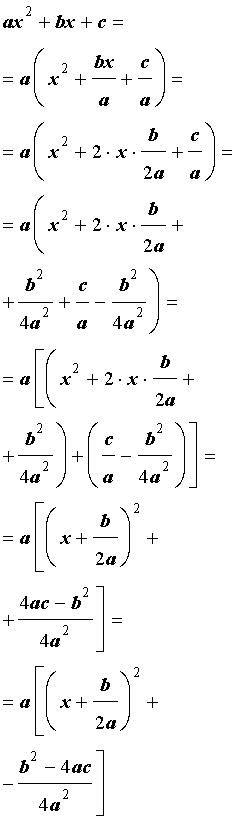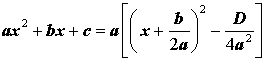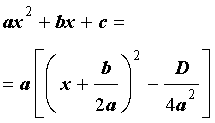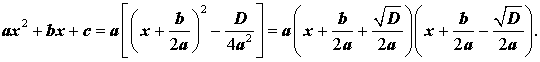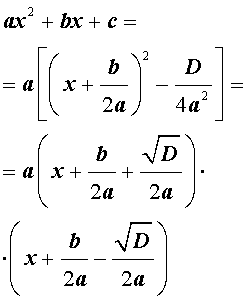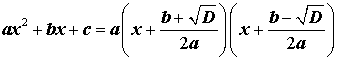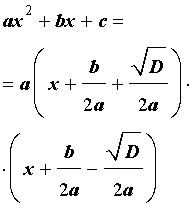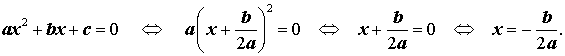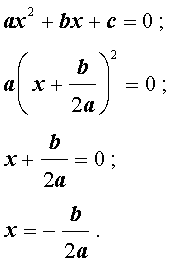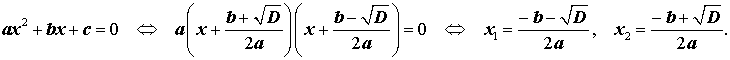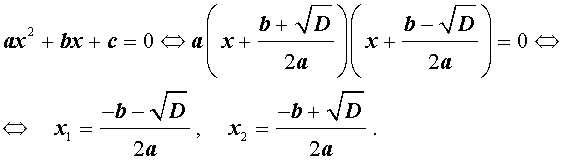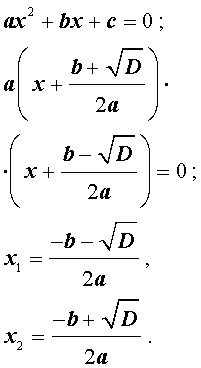Дискриминант
Дискриминантом квадратного трехчлена называют выражение \(b^<2>-4ac\), где \(a, b\) и \(c\) – коэффициенты данного трехчлена.
Например, для трехчлена \(3x^2+2x-7\), дискриминант будет равен \(2^2-4\cdot3\cdot(-7)=4+84=88\). А для трехчлена \(x^2-5x+11\), он будет равен \((-5)^2-4\cdot1\cdot11=25-44=-19\).
Дискриминант обозначается буквой \(D\) и часто используется при решении квадратных уравнений . Также по значению дискриминанта можно понять, как примерно выглядит график квадратичной функции (см. ниже).
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения:
— если \(D\) положителен – уравнение будет иметь два корня;
— если \(D\) равен нулю – только один корень;
— если \(D\) отрицателен – корней нет.
Это не надо учить, к такому выводу несложно прийти, просто зная, что квадратный корень из дискриминанта (то есть, \(\sqrt
Если дискриминант положителен
В этом случае корень из него – это некоторое положительное число, а значит \(x_<1>\) и \(x_<2>\) будут различны по значению, ведь в первой формуле \(\sqrt
Пример: Найдите корни уравнения \(x^2+2x-3=0\)
Решение:
Вычисляем дискриминант по формуле \(D=b^2-4ac\)
Найдем корни уравнения
Получили два различных корня из-за разных знаков перед \(\sqrt
На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение \(x^2+2x-3=0\) имеет корни \(x_<1>=1\) и \(x_<1>=-3\), значит при подстановке \(1\) и \(-3\) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию \(y=x^2+2x-3\) получим \(y=0\). То есть, функция \(y=x^2+2x-3\) проходит через точки \((1;0)\) и \((-3;0)\) (подробнее смотри статью Как построить график функции ).
Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
Формулы корней выглядят так: \(x_<1>=\) \(\frac<-b+\sqrt
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.
Пример: Найдите корни уравнения \(x^2-4x+4=0\)
Решение:
Вычисляем дискриминант по формуле \(D=b^2-4ac\)
Находим корни уравнения
Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.
На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция \(y=x^2-4x+4\) будет выглядеть вот так:
Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Пример: Найдите корни уравнения \(x^2+x+3=0\)
Решение
Вычисляем дискриминант по формуле \(D=b^2-4ac\)
Находим корни уравнения
Оба корня содержат невычислимое выражение \(\sqrt<-11>\), значит, и сами не вычислимы
То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение \(x^2+x+3\) получился ноль.
Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.
Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!
Квадратные уравнения
 Решение неполных квадратных уравнений Решение неполных квадратных уравнений |
 Выделение полного квадрата Выделение полного квадрата |
 Дискриминант Дискриминант |
 Разложение квадратного трехчлена на множители Разложение квадратного трехчлена на множители |
 Формула для корней квадратного уравнения Формула для корней квадратного уравнения |
 Прямая и обратная теоремы Виета Прямая и обратная теоремы Виета |
Квадратным трёхчленом относительно переменной x называют многочлен
| ax 2 + bx + c , | (1) |
где a, b и c – произвольные вещественные числа, причем
Квадратным уравнением относительно переменной x называют уравнение
| ax 2 + bx + c = 0, | (2) |
где a, b и c – произвольные вещественные числа, причем
Полным квадратным уравнением относительно переменной x называют уравнение
где a, b и c – произвольные вещественные числа, отличные от нуля.
Неполными квадратными уравнениями называют квадратные уравнения следующих типов:
 | 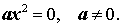 |
 | 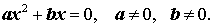 |
 | 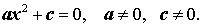 |
Решение неполных квадратных уравнений
Покажем, как решаются неполные квадратные уравнения на примерах.
Пример 1 . Решить уравнение
Пример 2 . Решить уравнение
| 2x 2 + 3x= 0 . | (3) |
Решение . Вынося в левой части уравнения (3) переменную x за скобки, перепишем уравнение в виде
| x (2x+ 3) = 0 . | (4) |
Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:
Ответ : 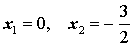
Пример 3 . Решить уравнение
Ответ : 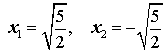
Пример 4 . Решить уравнение
| 3x 2 + 11 = 0 . | (5) |
Решение . Поскольку левая часть уравнения (5) положительна при всех значениях переменной x , а правая часть равна 0, то уравнение решений не имеет.
Ответ : 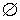
Выделение полного квадрата
Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:
Для того, чтобы получить формулу (6), совершим следующие преобразования:
Формула (6) получена.
Дискриминант
Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой D и вычисляется по формуле:
| D = b 2 – 4ac. | (7) |
Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.
Используя дискриминант, формулу (6) можно переписать в виде
Разложение квадратного трёхчлена на множители
Утверждение . В случае, когда 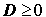
Доказательство . В случае, когда D = 0 , формула (8) и является разложением квадратного трехчлена на линейные множители:
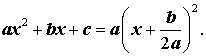 | (9) |
В случае, когда D > 0 , выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:
Таким образом, в случае, когда D > 0 , разложение квадратного трехчлена (1) на линейные множители имеет вид
В случае, когда D , выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.
Замечание . В случае, когда D , квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.
Формула для корней квадратного уравнения
Из формул (9) и (10) вытекает формула для корней квадратного уравнения .
Действительно, в случае, когда D = 0 , из формулы (9) получаем:
Следовательно, в случае, когда D = 0 , уравнение (1) обладает единственным корнем, который вычисляется по формуле
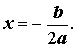 | (11) |
В случае, когда D > 0 , из формулы (10) получаем:
Таким образом, в случае, когда D > 0 , уравнение (1) имеет два различных корня , которые вычисляются по формулам
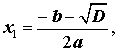 | (12) |
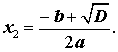 | (13) |
Замечание 1 . Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
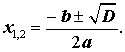 | (14) |
Замечание 2 . В случае, когда D = 0 , обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0 , квадратное уравнение (1) имеет два совпавших корня , вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
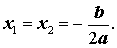 | (15) |
Замечание 3 . В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.
В случае, когда D = 0 , разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):
| ax 2 + bx + c = = a (x – x1) 2 . | (16) |
В случае, когда D > 0 , разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:
| ax 2 + bx + c = = a (x – x1) (x – x2) . | (17) |
Замечание 4 . В случае, когда D = 0 , корни x1 и x2 совпадают, и формула (17) принимает вид (16).
Прямая и обратная теоремы Виета
Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство
Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена
равны соответствующим коэффициентам многочлена
Таким образом, справедливы равенства
следствием которых являются формулы
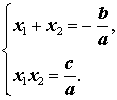 | (18) |
Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета) .
Словами прямая теорема Виета формулируется так: — «Если числа x1 и x2 являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».
Обратная теорема Виета формулируется так: — «Если числа x1 и x2 являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».
Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».
Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.
Разложение квадратного трёхчлена на множители
Алгоритм разложения квадратного трёхчлена на множители с помощью дискриминанта
Данный алгоритм является универсальным.
На входе: квадратный трёхчлен $ax^2+bx+c$
Задача: разложить трёхчлен на множители
Шаг 1. Находим дискриминант $D = b^2-4ac$
Шаг 2. Если $D \gt 0, x_1,2 = \frac<-b \pm \sqrt
Если D = 0, $x_0 = — \frac<2a>$ и $ax^2+bx+c = a(x-x_0 )^2$
Если $D \lt 0$, разложение на множители невозможно.
Шаг 3. Работа завершена.
Алгоритм разложения квадратного трёхчлена на множители по теореме Виета
Данный алгоритм применяется в частных случаях.
Если один (или оба) корня квадратного уравнения целые, то полезным навыком становится разложение на множители «в уме», с помощью теоремы Виета.
Навык этот не простой, и если у вас сразу не получится, не расстраивайтесь.
Рассмотрим следующий трёхчлен: $x^2+8x+15$
Если корни трёхчлена существуют, то их произведение равно 15.
Прикинем «в уме» соответствующие пары натуральных чисел:
В трёхчлене $c \gt 0$, значит корни одного знака, и в построении b участвует сумма этих корней. Из пары (1;15) сумма 8 не выходит, а вот из пары (3;5) — получается.
Для выбранной пары (3;5) запишем разложение, пока без знаков:
Теперь видно, что знаки в скобках – два плюса:
Рассмотрим другой трёхчлен: $x^2+2x-35$
Пары натуральных чисел, дающие произведение 35:
В трёхчлене $c \lt 0$, значит корни разных знаков, и в построении b участвует разность этих корней. Из пары (1;35) разность 2 не выходит, а вот из пары (5;7) — получается.
Для выбранной пары (5;7) запишем разложение, пока без знаков:
Теперь видно, что 7 должно быть с плюсом, а 5 – с минусом:
Обобщим алгоритм разложения по теореме Виета.
На входе: приведенный квадратный трёхчлен $x^2+bx+c$
Задача: разложить трёхчлен на множители при гипотезе, что корни — целочисленные
Шаг 1. Записать все пары натуральных чисел (m;n), дающих в произведении c.
Шаг 2. Если $c \gt 0$, то из всех пар выбрать ту, сумма которой даёт b.
Если $c \lt 0$, то из всех пар выбрать ту, разность которой даёт b.
Если выбрать пару не удаётся, данный алгоритм не подходит, и нужно приступить к разложению с помощью дискриминанта.
Шаг 3. Для выбранной пары записать разложение без знаков в виде:
Сопоставляя левую и правую части, окончательно расставить знаки в скобках.
Шаг 4. Работа завершена.
Предложенный алгоритм позволяет не только раскладывать на линейные множители трёхчлены, но и находить их корни, т.е. решать соответствующие квадратные уравнения.
Не забывайте менять знаки при записи решений уравнения!
Решаем $x^2+8x+15 = 0$. Получаем (x+3)(x+5) = 0. Корни $x_1 = -3, x_2 = -5$.
Решаем $x^2+2x-35 = 0$. Получаем (x-5)(x+7) = 0. Корни $x_1 = 5, x_2 = -7$.
При некотором опыте, можно наловчиться раскладывать не только приведенные трёхчлены, например:
$$ 5x^2-14x-3 = (5x+1)(x-3), 3x^2+13x-10 = (3x-2)(x+5), $$
В этих случаях алгоритм усложняется за счёт дополнительных вариантов расстановки коэффициентов при переменной в скобках.
Примеры
Пример 1. Разложите квадратный трёхчлен с помощью дискриминанта:
$ D = 7^2-4 \cdot 2 \cdot (-4) = 49+32 = 81 = 9^2 $
$ x = \frac<-7 \pm 9> <4>= \left[ \begin
Получаем: $2x^2+7x-4 = 2(x+4) \left(x- \frac<1> <2>\right)$
Можно также записать: $2x^2+7x-4 = (x+4)(2x-1)$
$ D = 20^2-4 \cdot 3 \cdot (-7) = 400+84 = 484 = 22^2 $
$x = \frac<-20 \pm 22> <6>= \left[ \begin
Получаем: $3x^2+20x-7 = 3(x+7) \left(x-\frac<1> <3>\right)$
Можно также записать: $3x^2+20x-7 = (x+7)(3x-1)$
$D = 19^2-4 \cdot 4 \cdot (-5) = 361+80 = 441 = 21^2$
$ x = \frac<19 \pm 21> <8>= \left[ \begin
Получаем: $4x^2-19x-5 = 4 \left(x+ \frac<1> <4>\right)(x-5)$
Можно также записать: $4x^2-19x-5 = (4x+1)(x-5)$
$ D = (\sqrt<2>)^2-4 \cdot \frac<1> <2>= 2-2 = 0, x = \frac<\sqrt<2>> <2>$
Получаем: $x^2-\sqrt <2>x+ \frac<1> <2>= \left(x- \frac<\sqrt<2>> <2>\right)^2 $
Пример 2*. Разложите трёхчлены на множители подбором по теореме Виета:
Пары множителей: (1;12),(2;6),(3;4)
$c = 12 \gt 0 \Rightarrow$ выбираем из пар ту, что в сумме дает b = 7. Это пара (3;4).
Записываем разложение без знаков: $(x…3)(x…4) = x^2+7x+12$
Расставляем знаки, результат: $x^2+7x+12 = (x+3)(x+4)$
Пары множителей: (1;18),(2;9),(3;6)
$c = -18 \lt 0 \Rightarrow$ выбираем из пар ту, разность которой дает b = 3. Это пара (3;6).
Записываем разложение без знаков: $(x…3)(x…6) = x^2+3x-18$
Расставляем знаки, результат: $x^2+3x-18 = (x-3)(x+6)$
Пары множителей: (1;77),(7;11)
$c = -18 \lt 0 \Rightarrow$ выбираем из пар ту, разность которой дает b=4. Это пара (7;11).
Записываем разложение без знаков: $(x…7)(x…11) = x^2+4x-77$
Расставляем знаки, результат: $x^2+4x-77 = (x-7)(x+11)$
Одна пара множителей (1;3)
Возможные разложения с коэффициентом:
$c = -3 \lt 0$, в скобках разные знаки.
Перебираем четыре возможных варианта и получаем:
$$2x^2-x-3 = (2x+3)(x-1) = 2 \left(x+ \frac<3> <2>\right)(x-1)$$
Пример 3. Сократите дробь.
Разложение на множители проводим по формулам сокращенного умножения, с помощью дискриминанта или по теореме Виета.
http://www.resolventa.ru/spr/algebra/kv.htm
http://reshator.com/sprav/algebra/8-klass/razlozhenie-kvadratnogo-tryohchlena-na-mnozhiteli/