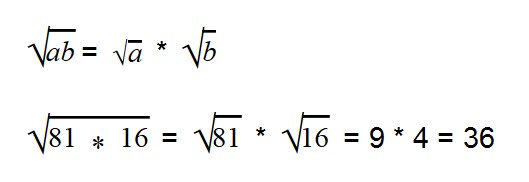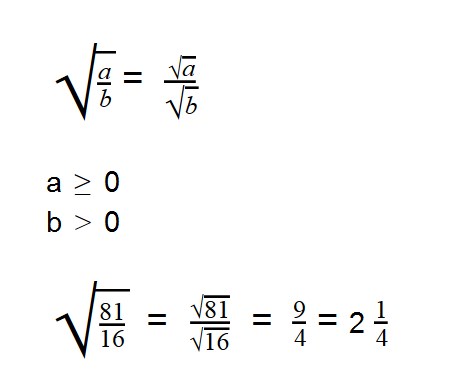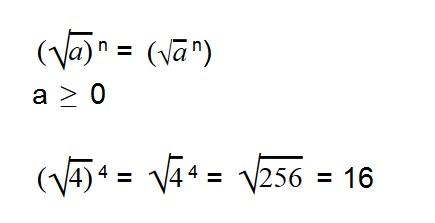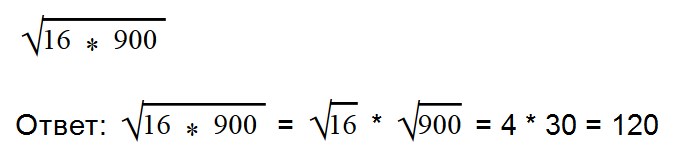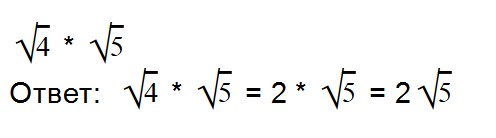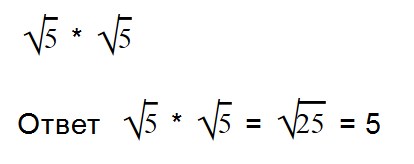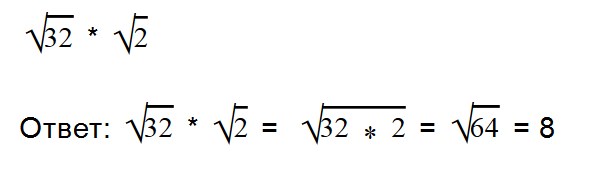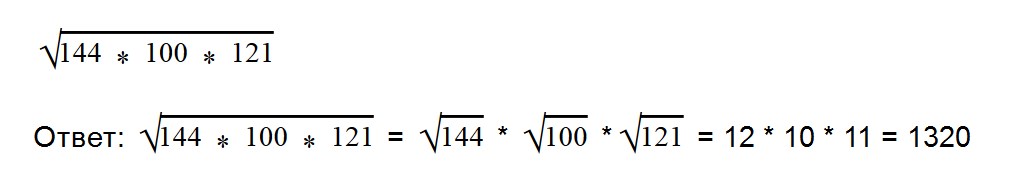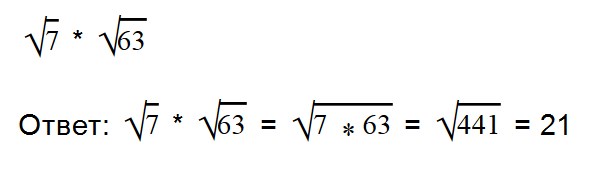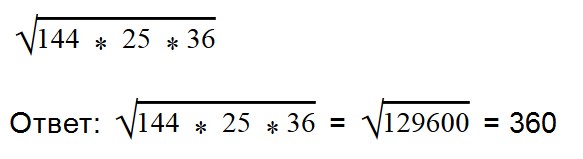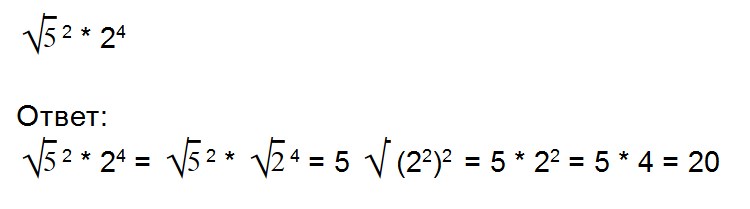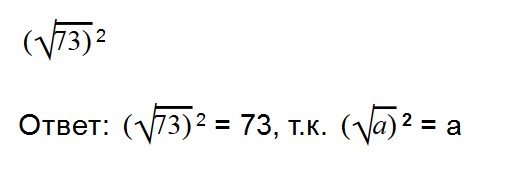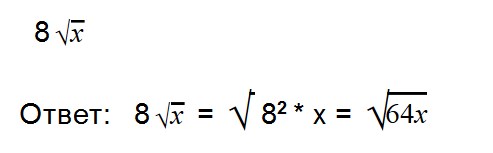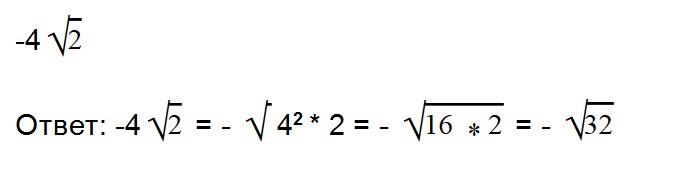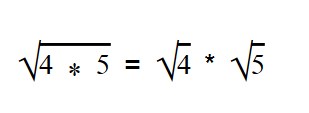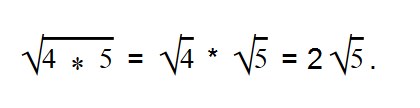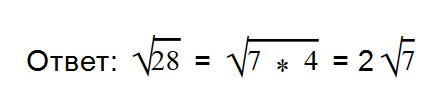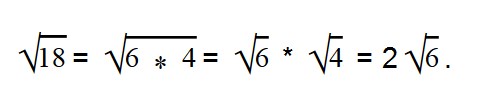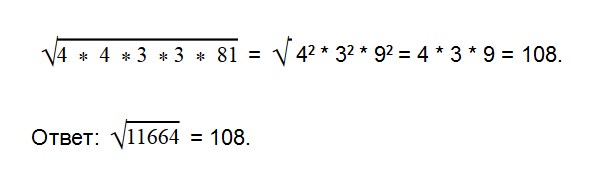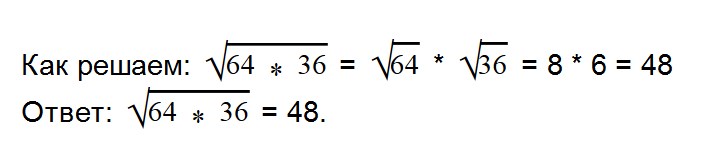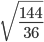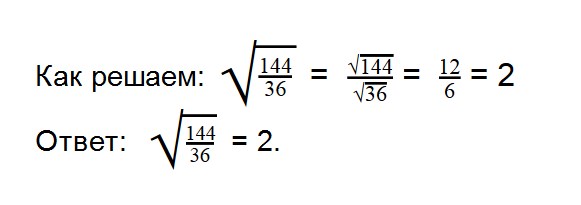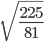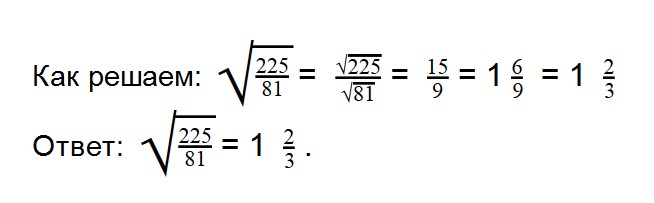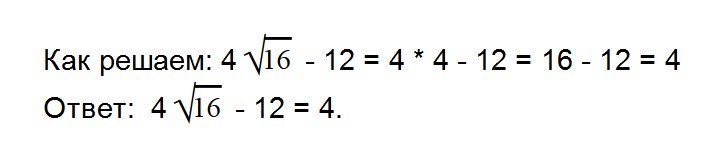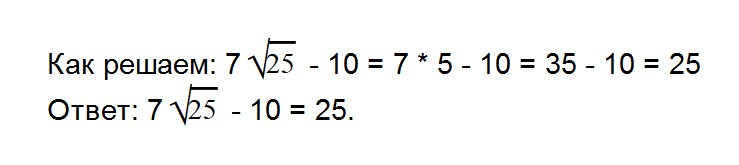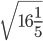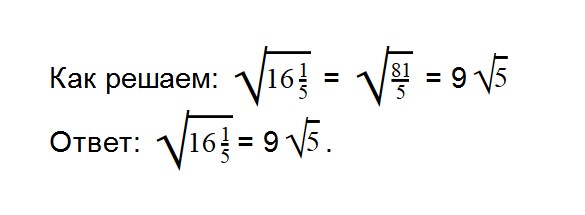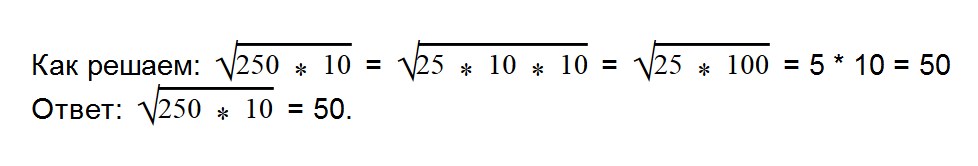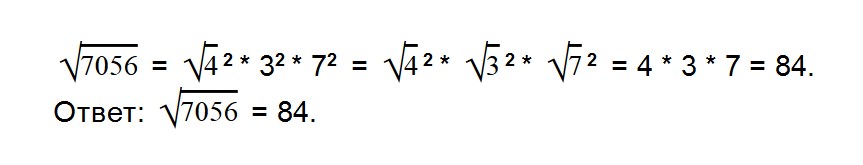Решение квадратных уравнений с применением циркуля и линейки
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Решение квадратных уравнений с применением циркуля и линейки
Выполнил.
Корни квадратного уравнения ах²+bx+c=0 (а≠0) можно рассматривать как абсциссы точек пересечения окружности с центром
Q, проходящей через точку А(0;1),
и оси Ох.
Решение уравнения сводится к построению на координатной плоскости окружности с центром Q и радиусом QA (для этого и понадобятся инструменты) и определению абсцисс точек пересечения окружности с осью Ох.
Возможны 3 случая:
1 случай
Если QA>то окружность пересекает ось Ох в двух точках М(х1 ; 0) и N( (х2 ; 0), уравнение имеет корни х1 , х2
х
у
Q
M
N
A
х1
х2
0
2 случай
Если QA= то окружность касается оси Ох в точке М(х1 ; 0), уравнение имеет корень х1 .
х
у
Q
M
A
х1
0
3 случай
Если QA -2,окружность
пересекает ох в двух
точках, уравнение имеет
2 корня.
Пример 3
Решите уравнение х²-4x+5=0.
Решение:
-в/2а=2, (а+с)/2а=3
Q(2;3), А(0;1)
QА
Курс повышения квалификации
Охрана труда
- Сейчас обучается 106 человек из 42 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 228 человек из 54 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 354 человека из 63 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 566 896 материалов в базе
Другие материалы
- 27.12.2020
- 1339
- 4
- 27.12.2020
- 1545
- 44
- 27.12.2020
- 1581
- 5
- 27.12.2020
- 574
- 4
- 27.12.2020
- 485
- 0
- 27.12.2020
- 447
- 0
- 27.12.2020
- 356
- 1
- 27.12.2020
- 506
- 3
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.11.2020 299
- PPTX 74 кбайт
- 3 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Цыренов Эрдэм Николаевич. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 31194
- Всего материалов: 236
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Рособрнадзор не планирует переносить досрочный период ЕГЭ
Время чтения: 0 минут
Новые курсы: управление детским садом, коучинг, немецкий язык и другие
Время чтения: 18 минут
Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.
Время чтения: 2 минуты
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
В Воронеже продлили удаленное обучение для учеников 5-11-х классов
Время чтения: 1 минута
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Окружности Карлейля, или Как решать квадратные уравнения циркулем и линейкой
Томас Карлейль. Портрет работы Дэниэла Маклиса
Казалось бы, какая может быть связь между квадратными уравнениями и геометрическими инструментами — циркулем и линейкой? Однако эта связь есть, и ее исследование с разных сторон — увлекательнейшая задача, тесно связанная и с геометрией, и с алгеброй.
А при чем тут Томас Карлейль? Согласно Википедии, это британский писатель, публицист, историк и философ, автор многотомных сочинений «Французская революция» (1837), «Герои, почитание героев и героическое в истории» (1841), «История жизни Фридриха II Прусского» (1858–1865). О его занятиях математикой практически ничего не известно, и тем не менее, в честь него назван класс окружностей, помогающих решать квадратные уравнения.
А теперь — обо всем по порядку.
Что мы подразумеваем под решением уравнений циркулем и линейкой?
В школьных учебниках геометрии есть какие-то упоминания о возможности построения квадратичных иррациональностей с помощью геометрических инструментов, но в основном не в виде практических алгоритмов построения, а в качестве теоремы существования. Единственный школьный пример конкретного алгоритма, как-то связанного с квадратными уравнениями, — построение среднего геометрического. Давайте и мы тоже начнем с этой задачи.
Задача 1. Даны отрезки \(a\) и \(b\). Постройте отрезок, равный \(\sqrt
Решение. Отложим на одной прямой \(AD = a\), \(DB = b\). Построим окружность на отрезке \(AB\) как на диаметре. Восставим к нему перпендикуляр в точке \(D\) — в пересечении получим точку \(C\) (рис. 1). Тогда \(CD=\sqrt
Рис. 1. Построение среднего геометрического
Обычно после решения этой задачи в школе говорится, что поскольку мы умеем с помощью циркуля и линейки складывать, вычитать, также умножать и делить (пользуясь теоремой Фалеса), а вот теперь умеем и корни извлекать, то этого уже достаточно для того, чтобы по формулам для корней квадратного уравнения научиться строить отрезки соответствующей длины. Действительно, достаточно. Но ведь дико неудобно!
К счастью, есть и нормальный способ «геометрического» решения квадратных уравнений, известный вот уже более двух веков. Этот способ впервые был описан шотландским математиком и физиком Джоном Лесли в его книге «Элементы геометрии и плоской тригонометрии», изданной в 1809 году. В одном из последующих изданий Лесли добавил сноску о том, что идея этого способа принадлежит его бывшему ученику Томасу Карлейлю.
Рис. 2. Задача Лесли, страница из его книги
На рисунке 2, заимствованном из книги Лесли, сформулирована задача: «Построить прямоугольник, равновеликий данному прямоугольнику \(CDFE\), полупериметр которого равен данному отрезку \(BC\)». Ее решение, предложенное Карлейлем, показано на рисунке 3. Прокомментируем построение на этом рисунке. Вначале данный отрезок \(BC\) откладывается на продолжении меньшей стороны четырехугольника \((CE)\). Затем на большей его стороне откладывается \(CG=CE\), после чего с помощью параллельных прямых достраивается четвертая вершина прямоугольника \(ABCG\). Теперь достаточно построить окружность на диаметре \(AD\) — точки \(J\) и \(K\) ее пересечения с отрезком \(BC\) и дадут искомые стороны прямоугольника (\(BJ\) и \(JC\) или, как изображено на рисунке, \(BK\) и \(KC=KI\)).
Рис. 3. Задача Лесли в Википедии
Почему и как это работает? Проще всего ответить на этот вопрос с помощью системы координат. Поместим начало координат в точку \(C\), ось абсцисс направим влево (к \(B\)), а ось ординат вверх (к \(D\)). Кроме того, будем считать, что \(CE=e\), \(CB=b\), \(CD=d\). Тогда координатами точки \(A\) будут \((b;\ e)\), а значит, координатами \(M\) будут \((b/2;\ (d+e)/2)\). Это означает, что окружность с центром \(M\) и радиусом \(MG\ (=MA=MD)\) имеет уравнение
\[\left(x-\frac b2\right)^2+\left(y-\frac
\[x^2-bx+\left(\frac b2\right)^2+y^2-(d+e)y+\left(\frac
Теперь уже совсем нетрудно увидеть, что точки пересечения этой окружности с горизонтальной прямой \(BC\) (осью абсцисс) — это точки, для которых \(y=0\), а значит, они удовлетворяют уравнению
Как мы знаем из школьной алгебры (теорема Виета), сумма корней этого уравнения равна \(b\), а произведение равно \(de\). Таким образом, если \(K\ (x_1;\ 0)\) и \(J\ (x_2;\ 0)\), то \(CK=CJ=x_1+x_2=b=CB\), а \(CK\cdot CJ=x_1\cdot x_2=de\), т. е. площадь прямоугольника со сторонами \(CK\) и \(BK=CJ\) действительно равна площади исходного прямоугольника \(CDFE\).
То же самое можно было получить и не выписывая уравнения окружности, из чисто геометрических соображений. Ведь \(CK\cdot CJ\) — это произведение длины секущей на ее внешнюю часть, a \(de=CD\cdot CG\) — другое такое же произведение. По теореме о секущих, они равны, т. е. \(CK\cdot CJ=de\). А так как \(ABCD\) — прямоугольная трапеция, а \(M\) — середина ее боковой стороны, то высота в равнобедренном треугольнике \(MJK\) является одновременно средней линией трапеции и медианой в том же треугольнике. Отсюда сразу получаем, что \(CK=BJ\), а значит, \(CK+CJ=CB=b\).
Осмысление того, что способ Карлейля годится не только для одной этой задачи, пришло далеко не сразу. Сначала в 1867 году австрийский железнодорожный инженер Эдуард Лиль описал свой метод приближенного графического нахождения корней многочленов произвольной степени (см. в Википедии «Метод Лиля»). Но только еще через 58 лет (в 1925 году) американский профессор Джордж Абрам Миллер, занимавшийся историей математики в качестве хобби, объяснил связь между окружностью, использованной Карлейлем и Лесли, и применением метода Лиля к решению квадратного уравнения.
Способ Карлейля
Итак, пусть мы хотим решить приведенное квадратное уравнение \(x^2-sx+p=0\). Тогда мы должны взять на координатной плоскости точки \(A\ (0;\ 1)\) и \(B\ (s;\ p)\), найти середину \(C\) отрезка \(AB\) и построить окружность с центром в \(C\) и радиусом \(CA\) (рис. 4). Точки пересечения этой окружности с осью абсцисс и будут корнями уравнения.
Рис. 4. Окружность Карлейля — определение
Доказательство практически полностью повторяет решение задачи Лесли, приведенное выше.
Но мы, кажется, собирались что-то строить циркулем и линейкой? А здесь координатная плоскость. Ничего страшного! Все, что нам на самом деле нужно от координат, вполне сводится к двум осям. Действительно, вместо точки \(B\ (s;\ p)\) можно сразу рассмотреть ее проекции на оси \(B_1\ (s;\ 0)\) и \(B_2\ (0;\ p)\). Ведь если мы знаем коэффициенты \(a\) и \(p\), то построить именно эти точки на осях — проще простого. А дальше центр окружности получится пересечением серединных перпендикуляров к \(OB_1\) и \(AB_2\) (постарайтесь разобраться, почему это так, по рисунку 5).
Рис. 5. Окружность Карлейля — построение
Как видно из рисунка 5, способ с окружностью Карлейля не только простой, но и удивительно легкий для запоминания. Кроме начала координат, требуются всего три точки — \(B_1\) (абсцисса которой равна коэффициенту \(s\)) откладывается на оси абсцисс, а \(A\ (0;\ 1)\) и \(B_2\) (ордината которой равна \(p\)) — на оси ординат. Два серединных перпендикуляра, одна окружность — вуаля, корни готовы!
Как это применять?
Возможно, самое известное применение окружностей Карлейля — построение правильных многоугольников. Многие слышали о том, что построение правильного пятиугольника циркулем и линейкой возможно. (На самом деле — не только возможно, но было дано и полностью обосновано еще Евклидом.) Но многие ли пытались понять, как именно решается эта задача?
Задача 2. Дана окружность с центром \(O\) и точка \(A\) на ней. Постройте правильный пятиугольник \(ABCDE\), вписанный в эту окружность.
Решение. Построение пятиугольника с помощью окружностей Карлейля отличается удивительной простотой. Начнем с координатных осей, проведя через центр круга прямую \(OX\), перпендикулярную \(OA\) (рис. 6). Радиус данной окружности будем считать равным 1. Теперь берем точку \(M\ (-1/2;\ 0)\) и строим окружность с центром \(M\), проходящую через \(X\). В пересечении с \(OA\) получаем точки \(H_1\) и \(H_2\). Если теперь в полученных точках построить единичные окружности, то они пересекут данную окружность как раз в точках \(B\), \(C\), \(D\), \(E\), являющихся вершинами правильного пятиугольника (на рисунке 6 он выделен красным, а единичные окружности — изображены синим пунктиром).
Рис. 6. Правильный пятиугольник
Почему это работает и при чем тут Карлейль? А вот при чем. Способ Карлейля утверждает, что построенная окружность с центром \(M\) находит корни квадратного уравнения для \(s;\ p)=(-1;\ -1)\), поскольку \(M\) — середина отрезка \(XY\), где координаты точки \(Y\) как раз и равны (\(-1;\ -1)\). Значит, \(H_1\) и \(H_2\) — корни квадратного уравнения \(x^2+x-1=0\). Это знаменитое уравнение золотого сечения. Для нас достаточно использовать его «тригонометрическую» ипостась.
Лемма. Корнями квадратного уравнения \(x^2+x=1\) являются величины \(2\cos72^<\circ>\) и \(2\cos144^<\circ>\).
Доказательство. Косинусы этих углов удовлетворяют тригонометрическому уравнению \(\cos3\alpha=\cos2\alpha\), при этом они отличны от корня \(\alpha=0\). Преобразование уравнения \(\cos3\alpha=\cos2\alpha\) в алгебраическое с помощью замены \(x=2\cos\alpha\) дает уравнение \((x-2)(x^2-x-1)=0\), что и требовалось доказать. (Корень \(x=2\) соответствует \(\alpha=0\).)
Итак, с помощью метода Карлейля и «золотой» леммы мы выяснили, что точки \(H_1\) и \(H_2\) имеют координаты \((2\cos144^<\circ>;\ 0)\) и \((2\cos72^<\circ>;\ 0)\) соответственно. А дальше мы в этих центрах построили единичные окружности, т. е. окружности того же радиуса, что и данная окружность с центром \(O\). Ясно, что они пересекут окружность \((O,\ A)\) на серединных перпендикулярах к отрезкам \(OH_1\) и \(OH_2\) соответственно. Осталось только понять, что серединные перпендикуляры — это прямые \(x=\cos72^<\circ>\) и \(x=\cos144^<\circ>\), а значит, точки \(B\), \(E\), \(C\) и \(D\) пересечения окружностей имеют координаты \((\cos72^<\circ>;\ \sin72^<\circ>)\), \((\cos72^<\circ>;\ -\sin72^<\circ>)\), \((\cos144^<\circ>;\ \sin144^<\circ>)\) и \((\cos144^<\circ>;\ -\sin144^<\circ>)\), т. е. углы \(AOB\) и \(AOE\) равны 72 градусам, а углы \(AOC\) и \(AOD\) — 144 градусам. А это и означает, что они являются вершинами правильного пятиугольника. Доказательство правильности построения на этом завершено.
О сложности построений и «геометрографии» Эмиля Лемуана
Француз Эмиль Мишель Гиацинт Лемуан по праву считается одним из отцов современной «геометрии треугольника». Вероятно, вы слышали о точке Лемуана в треугольнике или об окружностях Лемуана. Он же в 1892 году опубликовал работу «Геометрография, или искусство геометрических конструкций» («La Géométrographie ou l’art des constructions géométriques»), в которой впервые предложил сравнивать различные геометрические построения по количеству требуемых элементарных операций (а лучшим построением считать то, на которое тратится меньшее число операций). Оптимальным («геометрографическим») способом Лемуан называет самый экономный из известных алгоритмов построения.
Элементарных операций Лемуан насчитал пять:
\(S_1\) — приложить линейку к определенной точке;
\(S_2\) — провести прямую линию;
\(C_1\) — поставить ножку циркуля в определенную точку;
\(C_2\) — изменить радиус циркуля, поставив ножку с карандашом в определенную точку;
\(C_3\) — провести циркулем окружность.
При этом Лемуан считал циркуль устойчивым, т. е. после проведения окружности сохраняющим выставленный радиус. Таким образом, следующая окружность того же радиуса, по Лемуану, требует уже не трех операций: \(C_1+C_2+C_3\), а всего двух: \(C_1+C_3\).
Сосчитаем, например, количество операций в построении корней уравнения с помощью окружности Карлейля, показанном на рисунке 5. Оси координат и точки \(A\), \(B_1\) и \(B_2\) заданы. Построение серединного перпендикуляра к отрезку \(OB_1\) — это две окружности равных радиусов и одна прямая, т. е. \((2C_1+C_2+2C_3)+(2S_1+S_2)\). Следующий серединный перпендикуляр — это \((2C_1+2C_3)+(2S_1+S_2)\), потому что мы строим его, не меняя радиуса циркуля. Тем самым, мы построили центр, затратив 15 элементарных операций. И наконец, сама окружность Карлейля — это еще \(C_1+C_2+C_3\). Итого «сложность» построения \(5C_1+2C_2+5C_3+4S_1+2S_2\) равна 18.
Упражнение 1. Придумайте другой способ построения окружности Карлейля, имеющий сложность 17 или меньше.
Подсказка. Центр этой окружности — середина отрезка, одним из концов которого является \(B_1\). Постройте сначала второй конец этого отрезка.
Современная компьютерная игра-головоломка Euclidea (euclidea.xyz) также требует от решателей задач найти самое экономное построение, но, в отличие от Лемуана, не подсчитывает предварительные операции \(S_1\), \(C_1\) и \(C_2\), а считает только количество проведенных линий (т. е. \(S_2+C_3\) в терминологии Лемуана). С точки зрения Euclidea, построение окружности Карлейля имеет сложность 7.
Можно ли отыскать корни квадратного уравнения с меньшей сложностью?
Когда автор начинал писать эту статью, он предполагал, что этот вопрос будет повешен в качестве финальной улыбки Чеширского Кота и оставлен читателю для самостоятельного решения. Однако планы немножко поменялись, и сейчас я хочу показать более экономный способ, а читателям предложить обдумать, нельзя ли найти еще лучший.
Во-первых, откажемся от оси ординат. Зачем она нужна, если все корни мы ищем на оси абсцисс?
Пусть у нас есть всего одна ось, а на ней — четыре известные точки \(O\ (0)\), \(E\ (1)\), \(S\ (X+Y)\) и \(P\ (XY)\). Последние две точки соответствуют коэффициентам того уравнения, которое мы хотим решить. Рисунок 7 соответствует ситуации, когда \(0 Рис. 7. Четыре точки на одной оси
Вначале проведем две окружности равных радиусов с центрами в \(P\ (XY)\) и \(E\ (1)\) (рис. 8) — как будто мы хотим строить середину отрезка между этими точками. Радиус окружностей возьмем таким, чтобы первая окружность прошла через точку \(S\ (X+Y)\). Отметим \(C\) — общую точку этих окружностей.
Рис. 8. Начало построения
Затем построим еще две окружности — окружность с центром \(O\ (0)\), проходящую через \(C\), и окружность такого же радиуса с центром \(S\). Их точку пересечения (любую из двух точек) назовем \(D\) (рис. 9).
Рис. 9. Вторые две окружности
И (немного неожиданный, как и полагается улыбке Кота) финальный шаг — окружность с центром \(D\), радиус которой точно такой же, как у двух первых (рис. 10). Нетрудно убедиться, что в пересечении этой окружности с осью абсцисс получатся нужные корни уравнения. Так получается потому, что разность квадратов радиусов построенных окружностей равна \(XY\), и по теореме Пифагора квадрат длины отрезка между точками пересечения пятой окружности с прямой равен \((X+Y)^2-4XY=(X-Y)^2\). А поскольку середина этого отрезка имеет координату \((X+Y)/2\), то правый конец отрезка совпадает с большим из чисел \(X\), \(Y\), а левый — с меньшим.
Рис. 10. Корни уравнения найдены
Сосчитаем сложность: \(2C_1+C_2+2C_3\) на первую пару окружностей, столько же на вторую и еще \(C_1+C_2+2C_3\) на последнюю окружность — всего \(5+5+3=13\), вместо прежних 17 или 18. Ура!
Дополнение.
Построение правильного 17-угольника
Задача 3. Пусть дана окружность с центром \(O\) и точка \(A\) на ней. Постройте правильный 17-угольник с вершиной \(A\), вписанный в эту окружность.
Эта задача, в отличие от трех неразрешимых задач древности, стала знаменитой после того, как была решена 19-летним Карлом Фридрихом Гауссом. Биографы Гаусса пишут, что только после ее решения Гаусс окончательно выбрал своей будущей профессией математику, а не литературу. Известна также легенда, что Гаусс завещал выбить на своем могильном камне изображение правильного 17-угольника. Кажется, даже если такое завещание было, то оно оказалось невыполненным, а вот на памятнике Гауссу в Брауншвейге след его юношеской работы есть (рис. 11 и 12).
Рис. 11. Памятник Гауссу в Брауншвейге
Полное описание гауссова метода решения этой задачи, пожалуй, далеко выходит за рамки одной статьи, но набросок метода дать нетрудно. Правда, это потребует от читателя хорошего знакомства с комплексными числами.
Решение. Основной идеей Гаусса было циклическое упорядочение комплексных корней 17-й степени из 1 — такое, чтобы каждый следующий корень был определенной степенью предыдущего. Он доказал, что полный цикл получится тогда, когда эта определенная степень равна 3.
Далее Гаусс разбил этот цикл на два куска, которые он назвал периодами. В один период вошла половина корней — все корни на нечетных местах цикла, в другой — вторая половина:
Гаусс заметил, что сумма двух построенных им величин \(\eta_<02>+\eta_<12>\), равная сумме всех корней уравнения, равна \(-1\), а их произведение равно \(-4\). (Первое наблюдение Гаусса легко следует из теоремы Виета для уравнения \(x^<17>-1=0\), так как сумма всех корней вместе с корнем \(x=1\) равна 0. Второе же наблюдение несложно проверить непосредственным вычислением. Для этого достаточно просто перемножить выражения — каждое содержит по 8 слагаемых, в произведении их будет 64, и из соображений симметрии ясно, что каждая степень будет встречаться по 4 раза, поэтому произведение равно учетверенной сумме.) Иными словами, две эти величины — корни квадратного уравнения с известными коэффициентами.
Дальше — проще. Гаусс просто продолжает разбивать каждый период на два меньших:
Суммы значений \(\eta_<04>+\eta_<24>\) и \(\eta_<14>+\eta_<34>\) — уже известные нам величины \(\eta_<02>\) и \(\eta_<12>\), а их произведения равны \(-1\) (убедитесь в этом сами, раскрыв скобки в произведениях). Следовательно, мы снова знаем квадратные уравнения, корни которых нужно отыскать.
Следующим шагом точно так же вводятся периоды длины 2 — их всего восемь, от \(\eta_<08>\) до \(\eta_<78>\). Собственно, этот шаг уже является последним, потому что \(\eta_<08>=\tau^1+\tau^<16>=2\cos(\pi/17)\), так что, зная величину \(\eta_<08>\), мы легко построим вершины правильного 17-угольника, соседние с заданной вершиной \(A\) (аналогично построению вершин по точке \(H_2\) для правильного пятиугольника).
Рис. 12. Семнадцатиугольная звезда на памятнике
Квадратный корень из уравнения окружности
Что такое квадратный корень
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое квадратный корень
Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0
Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из √-16
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Если — 4, то -4 * -4 = 16, (минус на минус всегда дает плюс).
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Здесь могут возникнуть резонные вопросы, почему, например, в примере x 2 = 16, x = 4 и x = -4.
Разница между квадратным корнем и арифметическим квадратным уравнением
Прежде всего, чтобы разграничить эти два понятия, запомните:
- x 2 = 16 не равно x = √16.
Это два нетождественных друг другу выражения.
- x 2 = 16 — это квадратное уравнение.
- x = √ 16 — арифметический квадратный корень.
Из выражения x 2 = 16 следует, что:
- |x| = √16, это значит, что x = ±√16 = ±4, x1 = 4, x2 = -4.
Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.
В то же самое время, из выражения x = √16 следует, что x = 4.
Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:
- Пример решен неверно
- Это квадратное уравнение.
Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.
Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.
Даны два выражения:
Первое выражение — квадратное уравнение.
Второе выражение — арифметический квадратный корень.
Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.
Запись иррациональных чисел с помощью квадратного корня
Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.
Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.
Примеры иррациональных чисел:
Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.
Дано уравнение: x 2 = 2.
Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.
Переберем числа, чтобы удостовериться в этом:
1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.
Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.
Решение следующее:
Строим график функции y = x 2 .
Отмечаем решения на графике: -√2; √2.
Если попробовать извлечь квадратный корень из 2 с помощью калькулятора, то результат будет следующий: √2 = 1,414213… .
В таком виде ответ не записывают — нужно оставить квадратный корень.
x 2 = 2.
x = √2
x = -√2.
Извлечение корней
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.
Таблица квадратов
Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:
- 1. Извлеките квадратный корень: √289
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Влево — 1, вверх — 7.
- 2. Извлеките квадратный корень: √3025
Ищем в таблице число 3025.
Влево — 5, вверх — 5.
- 3. Извлеките квадратный корень: √7396
Ищем в таблице число 7396.
Влево — 8, вверх — 6.
- 4. Извлеките корень: √9025
Ищем в таблице число 9025.
Влево — 9, вверх — 5.
- 5. Извлеките корень √1600
Ищем в таблице число 1600.
Влево — 4, вверх — 0.
Извлечением корня называется нахождение его значение.
Свойства арифметического квадратного корня
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
- Корень произведения равен произведению корней
- Извлечь корень из дроби — это извлечь корень из числителя и из знаменателя
- Чтобы возвести корень в степень, нужно возвести в степень значение под корнем
Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.
Умножение арифметических корней
Для умножения арифметических корней используйте формулу:
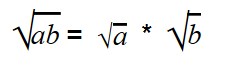 |
Примеры:
Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.
Если нет возможности извлечь корни из чисел, то поступаем так:
- Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:
Деление арифметических корней
Для деления арифметических корней используйте формулу:
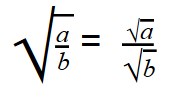 |
Примеры:
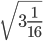
Ответ: смешанную дробь превращаем в неправильную (16 * 3) + 1 = 49
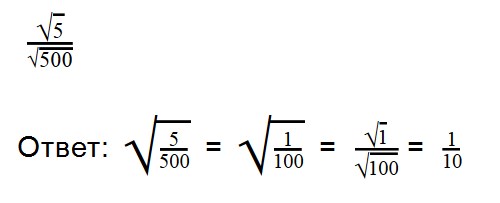
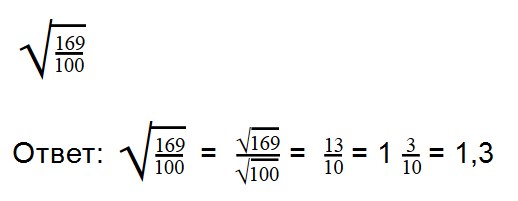
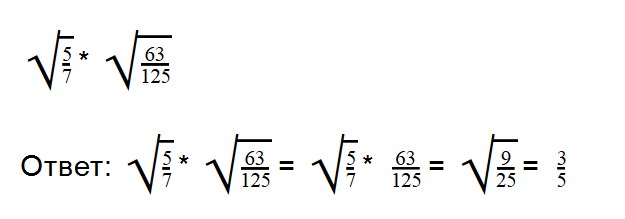
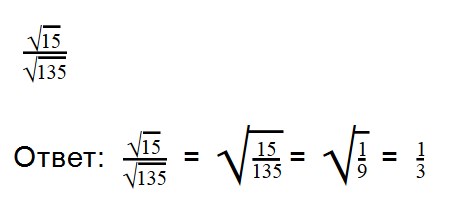
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.
Возведение арифметических корней в степень
Для возведения арифметического корня в степень используйте формулу:
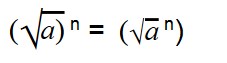 |
Примеры:
Эти две формулы нужно запомнить:
- (√a) 2 = a
- √a 2 = |a|
Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.
Внесение множителя под знак корня
Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.
А теперь давайте разберемся, как вносить множитель под знак корня.
Дано выражение: 7√9
Число семь умножено на квадратный корень из числа девять.
Извлечем квадратный корень и умножим его на 7.
В данном выражение число 7 — множитель. Давайте внесем его под знак корня.
Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.
Вы помните, что (√a) 2 = a
Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.
7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.
Формула внесения множителя под знак корня:
Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.
Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
Раскладываем подкоренное выражение на множители 28 = 7*4.
Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.
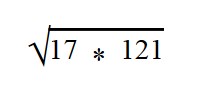
Ответ: по правилу извлечения квадратного корня из произведения,
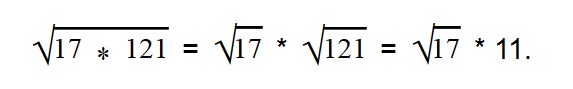
Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.
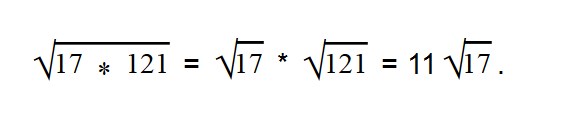
Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.
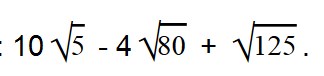
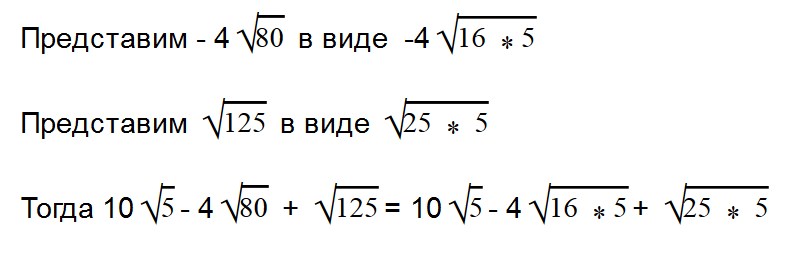
Вынесем в двух последних выражения множитель из-под знака корня.
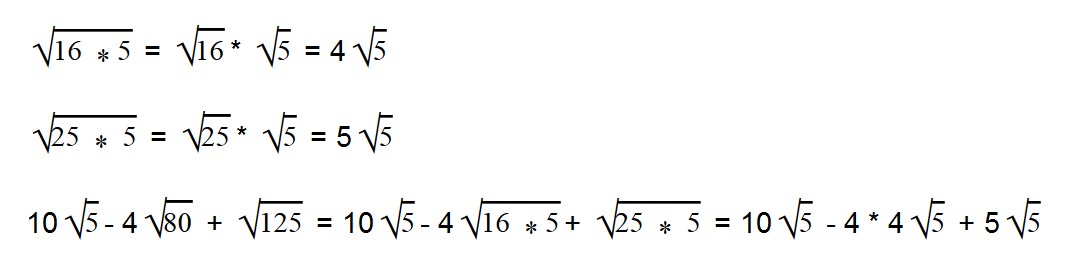
Умножаем (-4 * 4) = -16. Все остальное выражение записываем в неизменном виде.
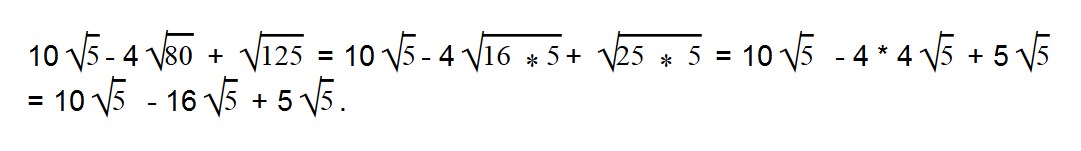
Мы видим, что во всем выражении есть один общий множитель — √5.
Выносим общий множитель за скобки:
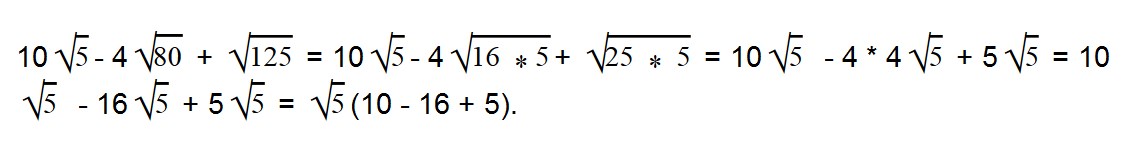
Далее вычисляем все, что в скобках:
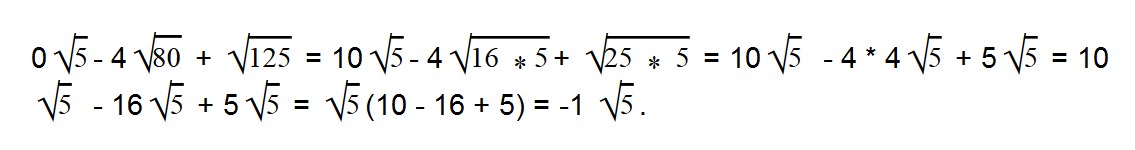
Сравнение квадратных корней
Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.
Если:
Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.
- Сравните два выражения: √50 и 9√5
Ответ: преобразовываем выражение 9√5.
9√5 = √81 * √5 = √81*5 = √405
Это значит, что 6√5 > √18.
Сравните два выражения: 7√12 и √20
Ответ: преобразовываем выражение 7√12.
7√12 = √49 * √12 = √49*12 = √588
Это значит, что 7√12 > √20.
Как видите, ничего сложного в сравнении арифметических квадратных корней нет.
Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.
Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.
Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.
Таких калькуляторов в интернете много, вот один из них.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
- Определить «сотни», между которыми оно стоит.
- Определить «десятки», между которыми оно стоит.
- Определить последнюю цифру в этом числе.
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
Мы видим что, 2116 больше 1600, но меньше 2500.
Это значит, что число 2116 находится между 40 2 и 50 2 .
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.
Как пользоваться таблицей
4 2 = 16 ⇒ 6
5 2 = 25 ⇒ 5
6 2 = 36 ⇒ 6
7 2 = 49 ⇒ 9
8 2 = 64 ⇒ 4
9 2 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Таким образом, у нас остаются два варианта: 44 2 и 46 2 .
Далее вычисляем: 44 * 44 = 1936.
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
Запишем выражение в следующем виде:
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
- 1. Вычислите значение квадратного корня: √36
- 2. Вычислите значение квадратного корня: √64*36
- 3. Вычислите значение квадратного корня:
- 4. Вычислите значение квадратного корня:
- 5. Вычислите значение квадратного корня:
- 6. Вычислите значение выражения: 4√16 — 12
- 7. Вычислите значение выражения: 5√9 — 8
- 8. Вычислите значение выражения: 7√25 — 10
- 9. Вычислите значение квадратного корня:
- 10. Вычислите значение квадратного уравнения:
- 11. Вычислите значение квадратного уравнения:
- 12. Извлеките квадратный корень из числа √7056 удобным вам способом
Как решаем:
Ответ: √0,81 = 0,9
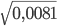
Как решаем:
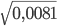 = 0,09
= 0,09Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
Ответ: 8√81 — 20 = 52.
Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
Ответ: 13√100 — 15 = 115.
Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24.
Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
Ответ: √36 + 2√9 = 12.
Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
Ответ: 2√16 — 3√25 = -7.
Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
Ответ: 3√81 — 5√9 = 12.
Как решаем: √60 = √15 * √4 = 2√15
Ответ: √60 = 2√15.
Как решаем: √160 = √16 * √10 = 4√10
Ответ: √160 = 4√10.
Как решаем: √6 2 * 7 = √36 * √7 = √252
Ответ: 6√7 = √252.
Как решаем: 8√2 = √8 2 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128.
Как решаем: 9√5 = √9 2 * 5 = √81 * √5 = √405
Ответ: 9√5 = √405.
Как решаем: (5 — √2) 2 = 5 2 — 2 * 5 * √2 + (√2) 2 = 25 — 10√2 + 2 = 27 — 10√2.
Ответ: (5 — √2) 2 = 27 — 10√2.
Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
Ответ: 3√49 — 3√25 = 6.
Как решаем: √484 * √576 = 22 * 24 = 528
Ответ: √484 * √576 = 528.
Как решаем: √625 * √81 = 25 * 9 = 225
Ответ: √625 * √81 = 225.
Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
Ответ: 3√100 — √144 = 18.
109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10
Квадратный корень. Действия с квадратными корнями. Модуль. Сравнение квадратных корней
Готовиться с нами — ЛЕГКО!
Эффективное решение существует!
Вы ищете теорию и формулы для ЕГЭ по математике ? Образовательный проект «Школково» предлагает вам заглянуть в раздел «Теоретическая справка». Здесь представлено пособие по подготовке к ЕГЭ по математике, которое фактически является авторским. Оно разработано в соответствии с программой школьного курса и включает такие разделы, как арифметика, алгебра, начала анализа и геометрия (планиметрия и стереометрия). Каждое теоретическое положение, содержащееся в пособии по подготовке к ЕГЭ по математике, сопровождается методически подобранными задачами с подробными разъяснениями.
Таким образом, вы не только приобретете определенные знания. Полный справочник для ЕГЭ по математике поможет вам научиться логически и нестандартно мыслить , выполнять самые разнообразные задачи и грамотно объяснять свои решения. А это уже половина успеха при сдаче единого государственного экзамена.
После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.
Факт 1.
\(\bullet\) Возьмем некоторое неотрицательное число \(a\) (то есть \(a\geqslant 0\) ). Тогда (арифметическим) квадратным корнем из числа \(a\) называется такое неотрицательное число \(b\) , при возведении которого в квадрат мы получим число \(a\) : \[\sqrt a=b\quad \text \quad a=b^2\] Из определения следует, что \(a\geqslant 0, b\geqslant 0\) . Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть \(100^2=10000\geqslant 0\) и \((-100)^2=10000\geqslant 0\) .
\(\bullet\) Чему равен \(\sqrt \) ? Мы знаем, что \(5^2=25\) и \((-5)^2=25\) . Так как по определению мы должны найти неотрицательное число, то \(-5\) не подходит, следовательно, \(\sqrt =5\) (так как \(25=5^2\) ).
Нахождение значения \(\sqrt a\) называется извлечением квадратного корня из числа \(a\) , а число \(a\) называется подкоренным выражением.
\(\bullet\) Исходя из определения, выражения \(\sqrt \) , \(\sqrt \) и т.п. не имеют смысла.
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число \(\sqrt2\) мы не можем. Представим, что \(\sqrt2\) – это некоторое число \(a\) . Соответственно, выражение \(\sqrt2+3\sqrt2\) есть не что иное, как \(a+3a\) (одно число \(a\) плюс еще три таких же числа \(a\) ). А мы знаем, что это равно четырем таким числам \(a\) , то есть \(4\sqrt2\) .
Факт 4.
\(\bullet\) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака \(\sqrt <> \ \) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа \(16\) можно, потому что \(16=4^2\) , поэтому \(\sqrt =4\) . А вот извлечь корень из числа \(3\) , то есть найти \(\sqrt3\) , нельзя, потому что нет такого числа, которое в квадрате даст \(3\) .
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt \) и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\) ), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\) ) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb \) .
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\) , равное расстоянию от точки \(a\) до \(0\) на вещественной прямой. Например, \(|3|\) и \(|-3|\) равны 3, так как расстояния от точек \(3\) и \(-3\) до \(0\) одинаковы и равны \(3\) .
\(\bullet\) Если \(a\) – неотрицательное число, то \(|a|=a\) .
Пример: \(|5|=5\) ; \(\qquad |\sqrt2|=\sqrt2\) . \(\bullet\) Если \(a\) – отрицательное число, то \(|a|=-a\) .
Пример: \(|-5|=-(-5)=5\) ; \(\qquad |-\sqrt3|=-(-\sqrt3)=\sqrt3\) .
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число \(0\) , модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная \(x\) (или какая-то другая неизвестная), например, \(|x|\) , про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: \(|x|\) . \(\bullet\) Имеют место следующие формулы: \[ >\] \[ >, \text a\geqslant 0\] Очень часто допускается такая ошибка: говорят, что \(\sqrt\) и \((\sqrt a)^2\) – одно и то же. Это верно только в том случае, когда \(a\) – положительное число или ноль. А вот если \(a\) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо \(a\) число \(-1\) . Тогда \(\sqrt =\sqrt =1\) , а вот выражение \((\sqrt )^2\) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что \(\sqrt\) не равен \((\sqrt a)^2\) ! Пример: 1) \(\sqrt =|-\sqrt2|=\sqrt2\) , т.к. \(-\sqrt2 ;
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
Извлечение корня из комплексного числа
Третий урок по комплексным числам. В этом уроке вы узнаете:
Начнём с ключевого определения.
1. Определение комплексного корня
Определение. Корнем $n$-й степени из комплексного числа $z$, где $n\in \mathbb $, $n \gt 1$, называется такое комплексное число $\omega $, что
т.е. $n$-я степень числа $\omega $ равна $z$.
Таких корней на множестве комплексных чисел всегда будет ровно $n$ штук. Все они обозначаются привычным знаком радикала:
Пример. Вычислить $\sqrt[3] $ на множестве комплексных чисел.
Очевидно, привычная нам единица является таким корнем, потому что $ ^ >=-1$. Но есть ещё два корня:
Итого три корня. Как и предполагалось.
Теорема. Для любого комплексного числа $z\ne 0$ существует ровно $n$ комплексных чисел, каждое из которых является корнем $n$-й степени из числа $z.$
Все эти корни считаются по следующей формуле.
2. Формула корней
Теорема. Пусть комплексное число записано в тригонометрической форме:
\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]
Тогда все корни степени $n$ из этого числа можно найти по формуле:
По сути, эта теорема является обратной к формуле Муавра:
Почему степень всегда одна, а корней несколько — об этом в конце урока. Сейчас для нас главное — алгоритм извлечения корня из комплексного числа. Он состоит из четырёх шагов:
- Перевести комплексное число в тригонометрическую форму;
- Записать общую формулу корня степени $n$;
- Подставить в эту формулу $k=0$, затем $k=1$ и так до $k=n-1$.
- Получим $n$ комплексных корней. Вместе они и будут ответом.
В ответе всегда будет набор из $n$ чисел. Потому что невозможно однозначно извлечь корень из комплексного числа $z\ne 0$.
Представим число $-8i$ в тригонометрической форме:
Запишем формулу корней в общем виде:
\[\sqrt[3] =2\cdot \left( \cos \left( -\frac \right)+i\sin \left( -\frac \right) \right)=\sqrt -i\]
В ответе нужно указать все три числа: $-2i$; $\sqrt -i$; $-\sqrt -i$.
Ещё раз: подставляя разные $k$, мы будем получать разные корни. Всего таких корней будет ровно $n$. А если взять $k$ за пределами диапазона $\left\ $, то корни начнут повторяться, и ничего нового мы не получим.
3. Геометрическая интерпретация
Если отметить на комплексной плоскости все значения корня $n$-й степени из некоторого комплексного числа $z\ne 0$, то все они будут лежать на окружности с центром в начале координат и радиусом $R=\sqrt[n] $. Более того: эти точки образуют правильный $n$-угольник.
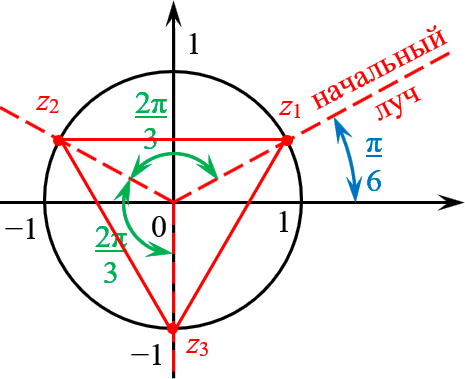
Отметить на комплексной плоскости все числа вида $\sqrt[3]$.
Представим число $z=i$ в тригонометрической форме:
Формула комплексных корней:
\[\sqrt[3] =1\cdot \left( \cos \left( \frac +\frac \right)+i\sin \left( \frac +\frac \right) \right)\]
Это три точки $ _ >$, $ _ >$ и $ _ >$ на окружности радиуса $R=1$:
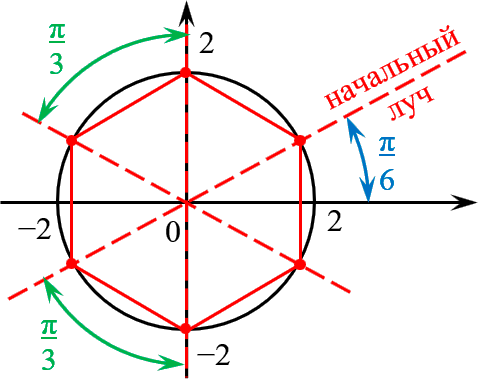
Получили правильный треугольник. Его первая вершина лежит на пересечении окружности радиуса 1 и начального луча, который образован поворотом оси $OX$ на угол $ / \;$.
Рассмотрим более сложный пример:
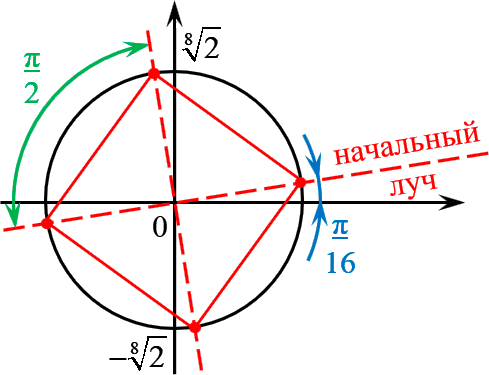
Отметить на комплексной плоскости все числа вида $\sqrt[4] $.
Сразу запишем формулу корней с выделением начального луча:
\[\sqrt[4] =\sqrt[8] \cdot \left( \cos \left( \frac +\frac \right)+i\sin \left( \frac +\frac \right) \right)\]
Отмечаем эти точки на комплексной плоскости. Радиус окружности $R=\sqrt[8] $, начальный луч $ / \;$:
И вновь всё чётко: четыре точки — правильный четырёхугольник, т.е. квадрат. С отклонением начального луча $ / \;$.
Ну и ещё один пример — вновь без промежуточных вычислений. Только формулировка задачи, формула корней и окончательный чертёж:
Отметить на комплексной плоскости все числа вида $\sqrt[6] $.
Формула корней с выделением начального луча:
\[\sqrt[6] =2\cdot \left( \cos \left( \frac +\frac \right)+i\sin \left( \frac +\frac \right) \right)\]
Получили правильный шестиугольник со стороной 2 и начальным лучом $ / \;$.
Таким образом, мы получаем «графический» алгоритм извлечения корня $n$-й степени из комплексного числа $z\ne 0$:
- Перевести число в тригонометрическую форму;
- Найти модуль корня: $\sqrt[n] $ — это будет радиусом окружности;
- Построить начальный луч с отклонением $\varphi = / \;$;
- Построить все остальные лучи с шагом $ / \;$;
- Получим точки пересечения лучей с окружностью — это и есть искомые корни.
Такой алгоритм прекрасно работает, когда аргумент исходного числа и отклонение начального луча $\varphi $ — стандартные «табличные» углы вроде $ / \;$. На практике чаще всего именно так и бывает. Поэтому берите на вооружение.:)
4. Почему корней всегда ровно n
С геометрической точки зрения, всё очевидно: если мы будем последовательно зачёркивать вершины правильного $n$-угольника, то ровно через $n$ шагов все вершины будут зачёркнуты. И для дальнейшего зачёркивания придётся выбирать вершину среди уже зачёркнутых.
Однако рассмотрим проблему с точки зрения алгебры. Ещё раз запишем формулу корня $n$-й степени:
Последовательно подставим в эту формулу указанные значения параметра $k$:
Очевидно, последняя строка получена при $k=n-1$. Подставим теперь $k=n$:
Поскольку синус и косинус — периодические функции с периодом $2\pi $, $ _ >= _ >$, и далее корни будут повторяться. Как мы и заявляли в самом начале урока.
5. Выводы
Ключевые факты из урока.
Определение. Корень степени $n$ из комплексного числа $z$ — это такое число $\omega $, что $ ^ >=z$.
Обозначение. Для обозначения комплексных корней используется знакомый знак радикала: $\omega =\sqrt[n] $.
Замечание. Если $z\ne 0$, таких чисел корней будет ровно $n$ штук.
Алгоритм нахождения корней состоит из двух шагов.
Шаг 1. Представить исходное число в тригонометрической форме:
\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]
Шаг 2. Воспользоваться формулой Муавра для вычисления корней:
Все полученные корни лежат на окружности радиуса $\sqrt[n] $ с центром в начале координат и являются вершинами правильного $n$-угольника. Первая вершина лежит на т.н. «начальном луче», который отклонён от положительной полуоси $OX$ на угол $ / \;$. Остальные вершины обычно легко находятся из соображений симметрии с помощью циркуля и линейки.
Геометрическую интерпретацию можно использовать для быстрого «графического» извлечения корней. Но это требует практики и хорошего понимания, что именно и зачем вы делаете. Технология такого извлечения корней описана выше в разделе «Геометрическая интерпретация».
Всё. В следующем уроке начнём решать уравнения в комплексных числах.:)
http://elementy.ru/nauchno-populyarnaya_biblioteka/436237/Okruzhnosti_Karleylya_ili_Kak_reshat_kvadratnye_uravneniya_tsirkulem_i_lineykoy
http://b4.cooksy.ru/articles/kvadratnyy-koren-iz-uravneniya-okruzhnosti