Квантовые состояния квантовые уравнения движения

Уравнение Шредингера. Уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях

Уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого вытекали бы волновые свойства частиц. Оно должно быть уравнением относительно волновой функции Ψ(х, у, z, t), так как величина │Ψ│ 2 определяет вероятность пребывания частицы в момент времени в объеме.

Основное уравнение сформулированоЭ. Шредингером: уравнения не выводится, а постулируется.

Уравнение Шредингера имеет вид:

— ΔΨ + U(x,y, z, t)Ψ = iħ , (33.9)

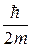
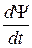
где ħ=h/(2π), т—масса частицы, Δ—оператор Лапласа, i— мнимая единица,U(x,y,z,t) — потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x,y, z, t) — искомая волновая функция частицы.

Уравнение (32.9) является общим уравнением Шредингера. Его также называют уравнением Шредингера, зависящим от времени. Для многих физических явлений, происходящих в микромире, уравнение (33.9) можно упростить, исключив зависимость Ψ от времени, иными словами, найти уравнение Шредингера для стационарных состояний — состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т. е. функцияU(x,y,z,t) не зависит явно от времени и имеет смысл потенциальной энергии.

∆Ψ + 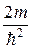(E—U)Ψ = 0. (33.10)

Уравнение (33.10) называется уравнением Шредингера для стационарных состояний.

В это уравнение в качестве параметра входит полная энергия Е частицы. Решение уравнения имеет место не при любых значениях параметра Е, а лишь при определенном наборе, характерном для данной задачи. Эти значения энергии называются собственными. Собственные значения Е могут образовывать как непрерывный и дискретный ряд.

33.5. Частица в одномерной прямоугольной «потенциальной яме с бесконечно высокими «стенками»

Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U (х) = соnstи ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. Энергия свободной частицы может принимать любые значения, т. е. ее энергетический спектр является непрерывным. Свободная квантовая частица описывается плоской монохроматической волной де Бройля, и все положения свободной частицы в пространстве являются равновероятными.

Проведем качественный анализ решений уравнения Шредингера применительно к свободной частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» (рис.33.1). Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)

где l — ширина «ямы», а энергия отсчитывается от ее дна (рис.33.1).

Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде

+ (Е- U)Ψ =0. (33.12)

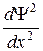
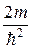
По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х=0 и х=l) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид

В пределах «ямы» уравнение Шредингера сведется к уравнению

+ ЕΨ =0. (33.14)

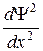
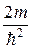
Стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Е_п зависящих от целого числа п.

Е_п= 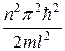,( n= 1, 2, 3, …).(33.15)

Следовательно, энергия Е_п частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е_п — называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Е_п, или, как говорят, частица находится в квантовом состоянии п. Частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная .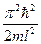

Туннельный эффект

Рассмотрим простейший потенциальный барьер прямоугольной формы (рис.33.2.а) для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U ширины l можем записать

0, х 1(для области 3),

При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е> U), либо отразится от него (при Е U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При Е l, т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из уравнения Шредингера, описывающего микрочастицы при условиях данной задачи.

Таким образом, квантовая механика приводит к специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер.

Для описання туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих.

Решение уравнения Шредингера для прямоугольной потенциального барьера дает формулу для коэффициента прозрачности:

D = D₀ exp( — 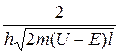), (33.16)

где U — высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D₀— постоянный множитель, который можно приравнять единице. Из этого выражения следует, что D сильно зависит от массы частицы, ширины барьера и от (U — Е); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.

С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия может сказаться достаточной для того, чтобы полная энергия частицы сказалась больше потенциальной.

Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций).

Квантовая песочница: часть 2

Квантовая песочница: часть 1
Что такое квантовое состояние? Чем обычное состояние отличается от квантового? В какой момент обычное состояние становится квантовым и что будет, если от него отнять квантовости? Оно всё еще будет квантовым или уже превратится в обычное? Оно же только что было квантовым. Наверное, оно стало запутанным, и кот тоже стал запутанным.

В данной статье постараемся ответить на эти вопросы и разобраться в сути квантовой механики.
Цель: написать простую программу, «имитирующую» квантовую эволюцию, чтобы наконец можно было пощупать эти кубиты ручками.

Оглавление:

• Часть I: Классическое состояние
• Часть II: Квантовое состояние
• Часть III: Кот
• Часть IV: Рой

Что такое обычное «состояние»? Этим термином пользуются так часто, что он начал восприниматься полностью интуитивно.

Часть I: Классическое состояние

Вопрос №1: «Дана частица P, которую можно наблюдать вдоль отрезка . Что такое состояние частицы P?»
Ответ: Классическое состояние частицы P — число из отрезка .

Внимательного читателя привлечет слово «наблюдать» — как это вообще понимать?
Оказалось, что все это время на участке были расположены какие-то «детекторы», которые «наблюдали», но почему мы о них ничего не сказали? И сколько их там вообще штук?

Мы сказали, что состояние частицы — число из отрезка . Мощность множества равна континууму — между нашими «границами» А и B находится бесконечно много чисел, причем они расположены бесконечно близко друг к другу — значит нам требуется бесконечно много детекторов для каждой точки? Звучит довольно затратно, не так ли?

А ведь, утверждая, что состояние есть число, мы, получается, подразумеваем именно это. Именно то, что у нас в наличии бесконечно много детекторов. Но ведь это не так. И такого не может быть в принципе.

На практике мы бы разбили отрезок на конечное число сегментов, а в пересечениях поставили бы детекторы, и каждый детектор был бы способен приближенно сообщить, есть ли частица в его окрестности или нет.

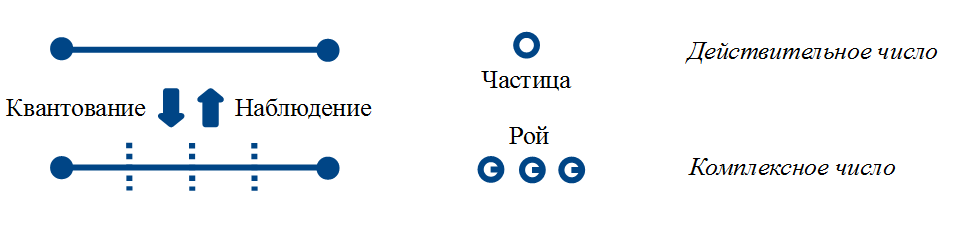
То, что было сделано выше называется квантованием. В данном случае мы провели квантование отрезка на сегменты. Квант — неделимая порция чего-либо в рамках используемой модели, абстрактный термин.

Самые интересные явления начинаются именно по той причине, что состояние частицы теперь перестало быть просто числом.

Часть II: Квантовое состояние

Вопрос №2: «Дана частица P, которую можно наблюдать только в окрестности некоторого числа детекторов на отрезке . Что такое состояние частицы P?»
Ответ: .

Дан отрезок и два детектора, расположенные в точках A и B.

Каждый детектор показывает какое-то определенное число, согласно которому мы можем определить, как далеко находится частица от данного детектора.

A — первый детектор, — его показания ( = 1, если частица попала прямо в А)
B — второй детектор, — его показания ( = 1, если частица попала прямо в В)

Выдвинем предположение о частице, чтобы как-то ограничить круг наших исследований:

Предположение: Частица одна, она не может просто так взять и клонировать себя.

Из этого предположения следует, что если частица в А, то она не может быть в В, и наоборот.

Или, что то же самое, если = 1, то = 0 и наоборот.

Теперь рассмотрим «движение» частицы от детектора А к детектору В. Частица была в А ( = 1, = 0), затем она начала лететь к В. Показания детектора А начали уменьшаться ( 0). Затем частица достигла детектора В и его показания равны = 1, а детектор А оповещает нас, что частицы в нем нет = 0.

Таким образом, мы описываем состояние частицы с помощью самих детекторов и их показаний.

Это запись означает, что конфигурация X включает в себя детектор A, показывающий нам число c1, и детектор B, показывающий нам число c2.

Вопрос №2: «Дана частица P, которую можно наблюдать только в окрестности детекторов, расположенных в точках A и B, которые являются квантованием отрезка на один сегмент . Что такое состояние частицы P?»
Предположение: Частица одна, она не может взять и просто так клонировать себя.
Ответ: Квантовое состояние частицы P — вектор двумерного гильбертова пространства с базисными векторами A = <1, 0>и B = <0, 1>. При этом этот вектор нормирован на единицу (), а базисные векторы A и B являются классическими состояниями из вопроса 1. Такие частицы также называют кубитами в силу двумерности базиса. Когда базис трехмерный, частицы называются кутритами и т. д.

Вопрос №2 (обобщенный): «Дана частица P, которую можно наблюдать только в окрестности конечного числа детекторов, расположенных в точках , которые являются квантованием отрезка на N — 1 сегмент . Что такое состояние частицы P?»
Предположение: Частица одна, она не может взять и просто так клонировать себя.
Ответ: Квантовое состояние частицы P — вектор N-мерного гильбертова пространства с базисными векторами . При этом этот вектор нормирован на единицу , а базисные векторы являются классическими состояниями из вопроса 1.

Часть III: Кот

Мы вплотную подошли к самым интересным проявлениям квантовой механики. Без сомнения каждый из читателей хоть краем уха слышал о таких терминах, как «квантовая суперпозиция» или «квантовая запутанность» — эти эффекты и другая подобная магия начинаются именно в тот момент, когда вы не будете делать тех умозаключений, которые не требуются.

У нас есть два определения состояния.

Определение №1: Классическое состояние частицы P — число из отрезка …
Предположение: Частица одна, она не может взять и просто так клонировать себя.
Определение №2: Квантовое состояние частицы P — вектор двумерного гильбертова пространства …

Обычно из каких-то определений выводят следствия, здесь же нас будет интересовать то, что не следует из определения, но мы все равно назовем это следствиями для стройности.

Следствие №1: Из определения квантового состояния не следует, что частица находится в одной точке отрезка. Вообще ниоткуда никак не следует.

То есть частица может находится сразу в двух точках! Например для частицы, которая находится в квантовом состоянии не следует, что она находится в одной точке. Да, может быть она где-то посередине, в какой-то точке M между A и B, но утверждая подобное, мы проявим необоснованную вольность.

Следствие №2: Из определения квантового состояния не следует, что частица разделилась на маленькие кусочки, одни кусочку полетели туда, а другие сюда.

Как это вообще понимать? Как частица может находится сразу в двух точках и при этом оставаться неделимой? Мы же привыкли, что кот Шрёдингера и жив, и мертв одновременно, значит и частица тоже и здесь, и там одновременно. Но ведь она же неделима. Она что растянулась?

Введем понятие роя и экземпляра виртуальных частиц.

Часть IV: Рой

Определение №3: Экземпляр частицы — виртуальный объект, которому соответствует положение в пространстве в данный момент времени, траектория движения с течением времени, а также комплексное число (называемое амплитудой), обладающее модулем и аргументом, для которого справедливы все алгебраические правила:
Определение №4: Рой — совокупность экземпляров.
Определение №5: Частица — рой (при выполнении операции квантования пространства).

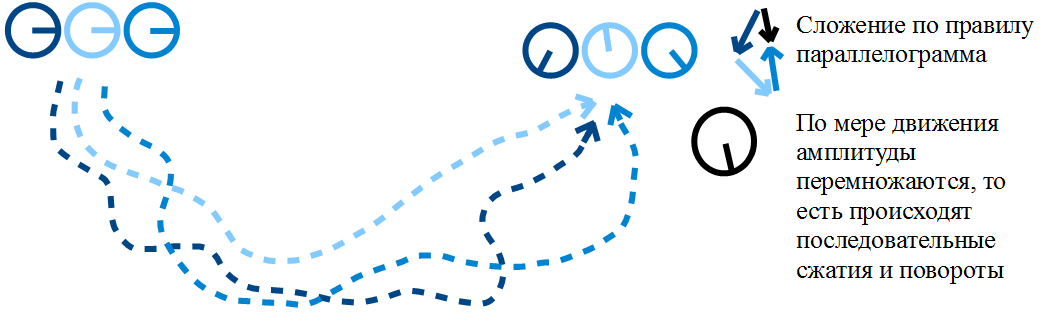
Представим экземпляр как шарик, внутри которого есть стрелка, соответствующая комплексному числу в комплексной плоскости. Важно понимать, что шарик может иметь одно направление движения, а стрелка внутри него — другое, то есть эти направления разные.

Но почему разные? Дело в том, что процессы внутри элементарной частицы настолько сложно описать, что влияние этих процессов на движение самой частицы невозможно предсказать на фундаментальном уровне, поэтому и связи между стрелкой внутри шарика и направлением движения самого шарика для нас не существует.

Словесные манипуляция, которые мы сейчас совершили, бесполезны, если не определить законы изменения величин r, φ и закон движения, ведь в них все и упирается.

Закон изменения аргумента: φ постоянно равномерно увеличивается на величину dφ по мере движения экземпляра.

Иными словами, наши комплексное стрелки постоянно крутятся в одном и том же направлении. Зачем это нужно? Чтобы система ни при каких обстоятельствах не перестала эволюционировать.

Закон сложения и умножения: По мере движения вдоль одной траектории амплитуды перемножаются. Амплитуды вдоль всевозможных траекторий складываются.

Данный закон также известен как «принцип суперпозиции в квантовой механике»

Закон движения экземпляров в пространстве:Пусть дана частица в квантовом состоянии. Дан экземпляр, которые находится в какой-то клетке пространства (над которым была произведена операция квантования на клетки). Вокруг этой клетки пространства есть соседние клетки.

1. Данный экземпляр клонирует себя столько раз, сколько вокруг него существует соседних точек
2. Каждый клон движется в ту соседнюю точку, которая ему соответствует
3. Данный экземпляр-отец движется в произвольную точку

Процесс повторяется для каждого экземпляра.

Мы не забываем, что внутри каждого шарика находится комплексная стрелка, которая имеет свое направление и длину. Как предсказать, какая результирующая стрелка окажется в произвольной клетке пространства в данный момент времени? Очевидно, для этого нужно знать, что было со всей системой в предыдущий момент времени. Мы получаем дифференциальное уравнение (его называют уравнением Шрёдингера в честь Шрёдингера, который его и открыл).

Закон движения экземпляров в пространстве: Пусть — квантовое состояние частицы, вектор-столбец, в котором одна за другой записаны амплитуды во всех клетках пространства. — оператор энергии, определяющий способ взаимодействия между экземплярами. Тогда рой движется согласно следующему закону: .

Формирование оператора энергии «по кусочкам ручками» будет рассмотрено в следующей статье.

Конструктивно, мы разобрались со следующими понятиями:

1. Классическое состояние частицы как число (а не как что-либо еще)
2. Квантовое состояние частицы как вектор (а не как «то, что находится сразу в нескольких местах»)
3. Частица как рой (при выполнении операции квантования)
4. Принцип суперпозиции роя, согласно которому амплитуды вдоль одной траектории перемножаются, а вдоль всевозможных траекторий складываются
5. Закон движения экземпляров

В следующей статье мы рассмотрим самое интересное — системы с произвольным количеством частиц. Разберем, что же такое тензоры, запутанные состояния и, наконец, напишем программу, способную «имитировать» квантовую эволюцию и удобно её отрисовывать.

Лекция №1. Квантов0механическ0е обоснование теории строения молекул и химической связи. Строение атома (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

КВАНТОВ0МЕХАНИЧЕСК0Е ОБОСНОВАНИЕ ТЕОРИИ СТРОЕНИЯ МОЛЕКУЛ И ХИМИЧЕСКОЙ СВЯЗИ. СТРОЕНИЕ АТОМА

2. Квантовомеханические особенности движения микрочастиц

3. Соотношения неопределённостей Гейзенберга

Учебная дисциплина «Строение вещества» охватывает теоретический базис современной химической науки. Освоение этого предмета предполагает создание основы для формирования современного научного мировоззрения естественно научной картины мира, приобретения необходимого уровня фундаментального теоретического образования.

В данном курсе лекций учтено, что студенты – химики нашего ВУЗА изучают квантовую механику и квантовую химию в пятом семестре, а дисциплину «Строение вещества» в четвёртом семестре. Поэтому в первых трёх лекциях рассматриваются основные постулаты квантовой механики, определяется физический смысл уравнения Шрёдингера, статистический смысл волновой функции.

В курсе лекций рассмотрены основные положения дисциплины «Строение вещества» — учение о строении веществ и химической связи, теория спектральных методов исследования молекул, химическая термодинамика (феноменологическая и статистическая).

При изложении теории химической связи, строения свойств молекул рассмотрены метод молекулярных орбиталей МО ЛКАО, широко применяемый сегодня в практике расчетов строения электронной структуры и реакционной способности молекул, и наиболее информативный экспериментальный метод исследования — молекулярная спектроскопия.

В разделе «Химическая термодинамика» детально рассмотрены современные методы расчета термодинамических свойств веществ и химического равновесия.

§ 2. Квантовомеханические особенности движения микрочастиц

Вещество состоит из атомов и молекул — микрочастиц. Состояния этих частиц, их движения описываются квантовой механикой. Среди других особенностей микрочастиц характерны следующие: полная энергия внутреннего движения атомов и молекул Е принимает строго определенные самой природой квантованные значения, набор таких значений E1, E2, E3. составляет дискретный спектр значений энергии. (Возможен также и непрерывный спектр.)

В 1923 году Луи де — Бройль выдвинул гипотезу о том, что корпускулярно — волновой дуализм присущ не только световым явлениям, но его можно распространить и на частицы вещества, т. е. он предположил, что частицы вещества наряду с корпускулярными свойствами обладают также и волновыми свойствами, а переход от корпускулярных свойств частиц к волновым устанавливается соотношениями:

,

Таким образом со всякой частицей вещества, обладающей импульсом Р и энергией Е, связана волна материи длиной

, а частота или .

Уравнение такой волны распространяющейся вдоль направления “x” с фазовой скоростью u

можно записать так: , где

, то или , т. е. групповая скорость равна скорости распространения частицы.

Отсюда можно было бы сделать вывод, что материальная частица представляет собой суперпозицию некоторой группы волн. Но этого сделать нельзя, так как такой пакет неустойчив и очень быстро расплывается.

Гипотеза де — Бройля была вскоре подтверждена экспериментально Девиссоном и Джермером.

Было установлено, что при отражении электронных пучков от поверхности металлов, число электронов, отраженных в некоторых направлениях, оказывается больше, а в некоторых — меньше, чем следовало ожидать, т. е. в этом случае наблюдается дифракция электронов, аналогичная дифракции рентгеновских лучей на кристаллах.

Последующие опыты Дж. Томсона, Тартаковского, Руппа и других показали, что прохождение электронов сквозь тонкие плёнки (металлические, слюдяные) сопровождаются появлением дифракционной картины.

Сделаем приблизительный расчёт длин волн де Бройля, которые встречаются в электронных пучках.

Так как по де – Бройлю: и при , а скорость электронов определяется величиной потенциала, приложенного между катодом и анодом электронно-лучевой трубки, т. е. откуда

то ;

Если подставить численные значения m, e, ћ, то получим

и при ; .

Таким образом, длины волн применяемых на практике электронных пучков лежат примерно в той же области, что и длины волн жёсткого рентгеновского излучения.

Позднее было показано, что не только электроны, по и протоны, нейтроны и даже молекулы Н2 и Не обладают волновыми свойствами: при их отражении от поверхности кристалла возникает дифракционная картина. Эти дифракционные эксперименты (Штерна его сотрудников — 1932 г.) с целыми атомами и молекулами показали, что волновые свойства не являются характерными только для электронов.

В настоящее время опыты по дифракции электронов и нейтронов и основанные на них приборы получили широкое распространение в науке и технике.

Преимущество электронной микроскопии перед рентгеноскопией состоит, во-первых, в том, что она позволяет получать значительно бóльшие интенсивности. Во-вторых, длину волны электронного пучка можно произвольно менять, меняя ускоряющий потенциал U.

Третье и наиболее важное преимущество электронных пучков связано с их способностью отклоняться под действием электрических и магнитных полей. Это явление вызвало появление электронной оптики и электронного микроскопа.

Разрешающая способность любого микроскопа определяется длиной волны применяемого излучения. Используя в электронном микроскопе большие ускоряющие напряжения, можно получить электроны с большими скоростями, а, следовательно, малые длины волн, тем самым повысить разрешающую способность электронного микроскопа.

Разрешающая способность современных электронных микроскопов, при u=50 ¸ 100 кВ. достигает 10¸25 Å.

§3. Соотношения неопределённостей Гейзенберга

В классической механике состояние материальной точки (классической частицы) определяется заданием значений координат, импульса, энергии и т. д. Перечисленные величины называются динамическими переменными. Строго говоря, микрообъекту не могут быть приписаны указанные динамические переменные. Однако информацию о микрочастицах мы получаем, наблюдая их взаимодействие с приборами, представляющими собой макроскопические тела.

Поэтому результаты измерений поневоле выражаются в терминах, разработанных для характеристики макротел, т. е. через значения динамических переменных. В соответствии с этим измеренные значения динамических переменных приписываются микрочастицам. Например, говорят о состоянии электрона, в котором он имеет такое-то значение энергии, и т. д.

Своеобразие свойств микрочастиц проявляется в том, что не для всех переменных получаются при измерениях определенные значения. Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты х и компоненты импульса рх. Неопределенности значений х и рх удовлетворяют соотношению

, (1.1)

(ћ — постоянная Планка). Из последнего выражения следует, что чем меньше неопределенность одной из переменных (х или рх), тем больше неопределенность другой. Возможно такое состояние, в котором одна из переменных имеет точное значение, другая переменная при этом оказывается совершенно неопределенной (ее неопределенность равна бесконечности).

Соотношение, аналогичное (1.1), имеет место для у и ру, для z и pz, а также для ряда других пар величин (в классической механике такие пары величин называются канонически сопряженными). Обозначив канонически сопряженные величины буквами А и В, можно записать

. (1.2)

Соотношение (1.2) называется соотношением неопределённостей для динамически сопряжённых величин A и В. Эти соотношения установил В. Гейзенберг в 1927 г.

Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку величины меньше постоянной Планка ћ, называется принципом неопределенностей Гейзенберга.

Энергия и время также являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей

Проявление свойств всякого физического объекта связано со взаимодействием его с другими объектами. В микромире все действия квантованы и пропорциональны постоянной Планка .

Конечность значения определяет механические соотношения для микромира.

В классической механике неточности возникающие из-за конечности кванта действия , не играют роли по причине малости его значения.

В механике микрочастиц нельзя пренебрегать конечностью значения кванта действия так же, как нельзя пренебрегать массой одной молекулы при рассмотрении плотности космического вакуума, или нельзя пренебрегать отклонением микрочастицы на величину радиуса атома от прямой при изучении рассеяния a — частиц на ядрах атома.

Следовательно, новое свойство, которое присуще микрообъектам при их взаимодействии, заключается в неопределённости тех критериев движения, которыми пользуется классическая механика.

Разделив левую и правую части принципа неопределённости на массу микрочастицы m будем иметь:

,

т. е. чем точнее определена скорость движения частицы в направлении «Х”, тем больше неопределенность в её координате X.

Надо ответить, что, так как волновые свойства частиц характеризуются длиной волны де-Бройля , то, в тех случаях, когда размеры области движения частицы или размеры амплитуды её колебаний велики по сравнению с , можно пользоваться законами и понятиями классической механики и они дадут достаточно точные результаты. Но если линейные размеры, характеризующие явления, сравнимы с длиной де-бройлевской волны частицы, то законы и понятия классической механики неприменимы.

КВАНТОВ0МЕХАНИЧЕСК0Е ОБОСНОВАНИЕ ТЕОРИИ СТРОЕНИЯ МОЛЕКУЛ И ХИМИЧЕСКОЙ СВЯЗИ. СТРОЕНИЕ АТОМА

1. Уравнение Шрёдингера

2. Свойства и физический смысл волновой функции

§1. Уравнение Шрёдингера

Подобно тому, как уравнения динамики Ньютона не могут быть получены теоретически и являются обобщением большого числа опытных фактов, основное уравнение квантовой механики также нельзя вывести из каких-либо известных ранее соотношений. Оно является исходным предположением, справедливость которого доказывается совпадением следствий, вытекающих из него, с опытными данными.

Основное уравнение квантовой механики было предложено в 1925 году

Э. Шредингером и носит его имя. Хотя уравнение Шредингера и не выводится, к его виду можно прийти путём следующих рассуждений.

В классической механике движение точечного тела описывается вторым законом Ньютона

Для того чтобы учесть волновые свойства частиц, необходимо, чтобы и уравнение движения было волновым.

Известно, что волновое уравнение является дифференциальным уравнением второго порядка в частных производных; независимыми переменными являются координаты и время.

Так, для плоской электромагнитной волны, распространяющейся в направлении «X» волновое уравнение можно представить в виде:

1.

2.

Состояние микрочастицы в квантовой механике описывается волновой функцией, которая обозначается y.

Волновое уравнение y — функции запишется так:

,

где u — скорость распространения волн де-Бройля.

Решением этого уравнения при движении микрочастицы вдоль оси Х является уравнение бегущей волны:

Дифференцируя дважды по t будем иметь:

Подставляя полученное выражение в волновое уравнение — функции имеем:

, или , но

, а , следовательно ,

с другой стороны . Таким образом .

Если, то окончательно будем иметь:

Или

где Е — полная энергия частицы, U — потенциальная энергия частицы.

Если частица движется в любом направлении, то полученное уравнение будет иметь вид:

где .

Полученное уравнение носит название стационарного уравнения Шредингера.

Состояние микрочастицы с учётом зависимости y — функции от координат и времени описывается полным волновым уравнением Шредингера:

Необходимо отметить, что уравнение Шредингера справедливо лишь при скоростях движения частиц

Волновое уравнение справедливое для движения частиц со скоростями (релятивистское волновое уравнение) было получено Дираком.

Дальнейшее развитие квантовая (волновая) механика получила в трудах Гейзенберга, Дирака и других физиков.

§2. Свойства и физический смысл волновой функции

Волновая функция y представляет собой полную квантовую характеристику состояния микрочастиц. Она характеризует состояние частицы и играет ту же самую роль, что и напряжённость электрического и магнитного полей в электромагнитном поле волны для фотона.

Волновая функция y может принимать положительные значения и отрицательные значения и характеризует дифракционные явления потоков микрочастиц.

Основное утверждение квантовой механики заключается в том, что величина пропорциональна вероятности нахождения частицы в объёме DV. Таким образом, уравнение Шредингера дает только вероятность нахождения частицы в определённой области пространства.

Если, например, электрон находится в таком состоянии, что он локализован в малой области пространства, то y — функция этого состояния электрона вне этой области обращается в нуль.

Для того чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна удовлетворять следующим условиям:

1. Функция y должна быть непрерывной, конечной, однозначной и иметь непрерывную первую производную.

2. Т. е. она не должна изменяться скачком и давать однозначное значение вероятности состояния частицы.

В определенных случаях одному и тому же значению энергии Е системы (частицы) могут отвечать несколько состояний, описываемых разными волновыми функциями. Такие состояния называются вырожденными, соответственно дважды или трижды вырожденными и т. п.

Собственные функции Ψ уравнения Шредингера, принадлежащие разным собственным значениям ортогональны. Можно показать, что области нахождения частицы в состояниях Ψi и Ψj взаимно не налагаются. То есть

, (1.2)

где — символ Кронекера. Принадлежащие одному и тому же собственному значению Еi вырожденные собственные функции Ψi1, Ψi2 и т. д. не обязательно ортогональны, но из линейных комбинаций этих функций может быть построена система ортогональных функций.

Уравнение Шредингера решается с точностью до произвольного множителя, т. е. если ему удовлетворяет функция Ψi то ему уже удовлетворяет и функция cΨi где c — любое число. Для однозначности решения исходят из физической сущности Ψ-функции.

Волновая функция должна удовлетворять условию нормировки, т. е. для неё должно выполняться равенство:

,

или , где — величина комплексно-сопряжённая функции y.

Физический смысл данного утверждения состоит в том, что при определённых условиях частица заведомо будет где-нибудь обнаружена. Т. е., что вероятность обнаружения частицы во всём пространстве равна 1, — вероятность достоверного события. Таким образом, в квантовой механике, вероятности входят непосредственно в фундаментальные механические соотношения как характеристические величины, а не как результаты недостаточности знаний механических деталей движения микрочастиц.

Простейшие задачи квантовой механики

1. Прохождение микрочастиц через одномерный высокий потенциальный барьер конечной ширины.

2. Прохождение частицы над одномерной бесконечной ступенькой

3. Движение микрочастицы в одномерном прямоугольном потенциальном ящике с бесконечно высокими стенками.

4. Задача об одномерном гармоническом квантовом осцилляторе.

§1. Прохождение частицы через одномерный высокий потенциальный барьер конечной ширины

Высоким одномерным потенциальным барьером прямоугольной формы называется внешнее силовое поле, имеющее следующую конфигурацию:

Рассмотрим данную задачу с точки зрения классической механики и с точки зрения квантовой механики.

Так как энергия частицы, налетающей на барьер меньше высоты барьера, то из законов классической механики следует, что частица не может перейти из области I в область III, так как внутри барьера , то есть закон сохранения энергии запрещает переход частицы из области I в область III при данных численных соотношениях между энергиями. Поэтому, доходя до точки x=0 частица абсолютно упруго отражается и движется в обратном направлении с той же энергией и скоростью.

С точки зрения квантовой механики:

Решение уравнения Шредингера показывает, что существует отличная от 0 вероятность того, что частица переходит из области I в область III. Данное явление называется туннельным эффектом. В данном случае противоречие снимается, так как полную энергию системы нельзя разделить на кинетическую и потенциальную – это запрещается соотношением неопределенностей, так как . А из соотношения неопределенностей следует, что нельзя одновременно измерить .

Найдем вероятность того, что частица перейдет из области I в область III – эта вероятность называется коэффициентом прозрачности барьера

Для области II:

Для области III:

Заменим: и получим следующие выражения:

для областей I и III:

для области II:

Для области II:

В первом уравнении системы (5.1) первое слагаемое определяет волну вероятности для частицы, налетающей на переднюю стенку потенциального барьера, A1 – весовой коэффициент. Второе слагаемое описывает волну вероятности частицы, отраженной от передней стенки барьера. Во втором уравнении первое слагаемое описывает волну вероятности для микрочастицы, налетающей на заднюю стенку барьера (x=d). Второе – волна вероятности для частицы отраженной от задней стенки барьера. В третьем уравнении первое слагаемое определяет волну вероятности для частицы, прошедшей через барьер в область III, второе слагаемое описывает волну вероятности для частицы отраженной в области III. А так как в области III нет центров отражений, то второе слагаемое должно быть равно 0, то есть окончательно система примет вид:

вероятность того, что частица налетела на переднюю стенку барьера.

вероятность того, что частица прошла через барьер.

Чтобы найти коэффициент прозрачности D нужно воспользоваться непрерывностью волновой функции на передней и задней стенке барьера и непрерывностью первой производной на тех же границах:

Так как в коэффициент прозрачности входят амплитуды вероятности частицы, падающей на переднюю стенку и частицы, прошедшей через барьер, то отраженными волнами можно пренебречь.

Вероятность прохождения частицы через барьер зависит от ширины барьера и от разности .

Туннельный эффект – реальное физическое явление, которое наблюдается в природе. Например, одним из видов радиоактивного распада является – распад:

С точки зрения классической физики – распад энергетически невозможен, так как энергия частицы внутри ядра , а высота барьера

§2. Прохождение частицы над низкой бесконечно длинной ступенькой

Если рассматривать эту задачу используя законы классической механики: частица, движущаяся из , проходит над ступенькой и движется в с уменьшенной кинетической энергией, то есть вероятность того, что частица отразится от ступеньки равна 0.

Если рассматривать эту задачу, используя законы квантовой механики, то существует вероятность (отличная от 0) того, что частица отразится на границе областей I и II.

Для области I:

Для области II:

Волновые числа в областях I и II: и

Корни характеристического уравнения мнимые, поэтому решения гармонические:

В первом уравнении первое слагаемое определяет волну вероятности для частицы, идущей из к ступеньке, второе слагаемое описывает волну вероятности для частицы, отразившейся на границе областей I и II (x=0). Во втором уравнении первое слагаемое описывает волну вероятности для частицы, прошедшей над ступенькой слева–направо, а второе слагаемое – волну вероятности для отраженной частицы в области II, так как ступенька бесконечно длинная B2=0.

Найдем коэффициент отражения частицы от ступеньки и коэффициент прохождения:

Воспользуемся непрерывностью волновой функции на границе областей в точке x=0, условием гладкости функции и условием непрерывности первой производной.

КВАНТОВ0МЕХАНИЧЕСК0Е ОБОСНОВАНИЕ ТЕОРИИ СТРОЕНИЯ МОЛЕКУЛ И ХИМИЧЕСКОЙ СВЯЗИ. СТРОЕНИЕ АТОМА

1. Водородоподобные ионы

2. Атомные орбитали водородоподобных ионов

3. Спин электрона

4. Многоэлектронные атомы

§1. Квантово-механическая теория водородоподобных ионов.

Атом это устойчивая динамическая система, состоящая из положительно заряженного ядра и определенного числа электронов. У атома как устойчивой системы энергия ниже, чем суммарная энергия невзаимодействующих ядра и электронов, принимаемая обычно за нуль. Энергия электрона в атоме при таком отсчете оказывается отрицательной.

Простейший из атомов — водородоподобный ион состоит из ядра с зарядом +Ze и одного электрона с зарядом — e, где Z – число протонов в ядре,

При Z = 1 это атом Н, при Z = 2 — ион Не+ и т. д.

В водородоподобном атоме электрон движется в центрально-симметричном кулоновском поле ядра. Считая ядро неподвижным, всю энергию Е атома можно рассматривать как сумму кинетической энергии электрона Т и его потенциальной энергии U в поле ядра.

Набор допустимых значений энергии Е стационарных состояний атома и соответствующие им волновые функции Ψ определяют, решая уравнение Шредингера.

Электрон в водородоподобных ионах движется в кулоновском поле ядра. Кулоновское поле — поле точечного заряда. Ядро можно считать точечным зарядом, так как его размер (rя) в 105 раз меньше размера атома.

Потенциальная энергия электрона в кулоновском поле ядра равна

,

где ε0 = 8,85·10-12 Ф/м – электрическая постоянная, r – среднее расстояние от центра ядра до положения электрона в данном квантовом состоянии. Знак «-“ означает, что электрон находится в потенциальной яме ядра.

В этом случае стационарное уравнение Шредингера будет иметь вид:

Поскольку кулоновское поле является центрально-симметричным, то для решения этого уравнения, удобно воспользоваться сферической системой координат: r, q, j. Данный переход иллюстрируется (рис.4.1):

x=r·sinθ·cosφ; y=r·sinθ·sinφ; z = r·cosθ; .

Бесконечно малый элемент объёма в сферической системе координат имеет вид dv = r2 sinθ·dθ·dφ·dr.

Дифференциальный оператор Лапласа в сферической системе координат имеет вид

,

а стационарное уравнение Шредингера запишется следующим образом:

. (4.1)

Решение этого уравнения представляет собой сложную задачу. Можно показать, что точное решение этого уравнения для электрона в атоме водорода приводит к появлению дискретных энергетических уровней.

Т. е. функция y имеет однозначные, конечные и непрерывные решения только в случаях:

1. при любых положительных значениях Е (полной энергии) Е>0. Этот случай соответствует электрону, пролетающему вблизи ядра и удаляющемуся вновь на бесконечность;