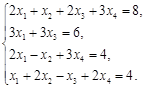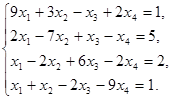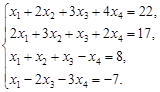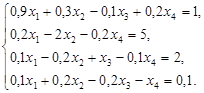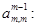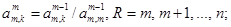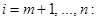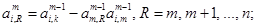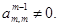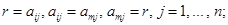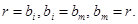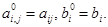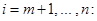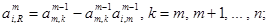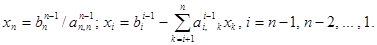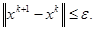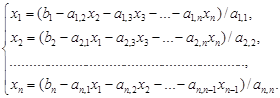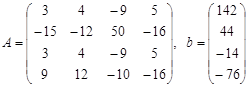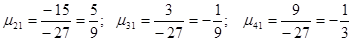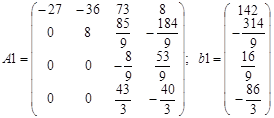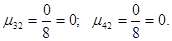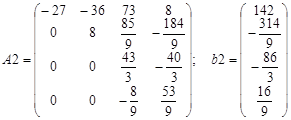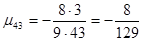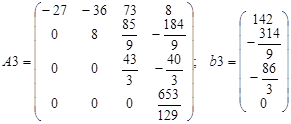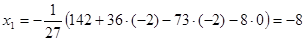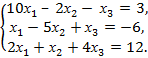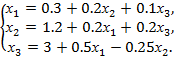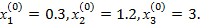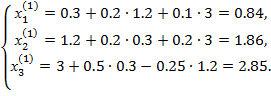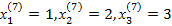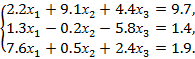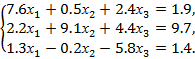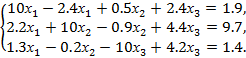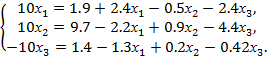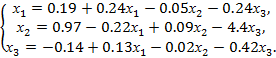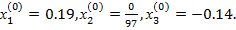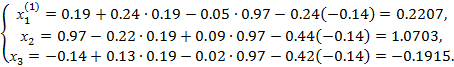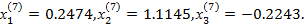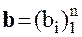Лабораторная_работа «Решение системы линейных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Матричные методы решения систем линейных алгебраических уравнений
Цель работы: приобрести навыки решения линейных алгебраических уравнений в среде Excel .
1. Изучить представленный ниже материал, повторить приведенные примеры
В общем виде система линейных алгебраических уравнений записывается следующим образом:
Эту систему можно представить в матричном виде: AX = b , где



Метод обратной матрицы
Систему линейных алгебраических уравнений AX = b умножим слева на матрицу, обратную к матрице А . Система уравнений примет вид:
Вектор неизвестных вычисляется по формуле X=A -1 b .
В этом случае неизвестные x 1 , x 2 ,…, x n вычисляются по формуле:
где – определитель матрицы A ;
I – определитель матрицы, получаемой из матрицы А путем замены i -го столбца вектором b.
Рассмотрим решение системы линейных уравнений методом обратной матрицы и методом Крамера на следующих примерах.
Решить систему линейных уравнений методом обратной матрицы:
Матрица коэффициентов А и вектор свободных коэффициентов b имеют вид:

.
Введем эти данные в рабочий лист Excel (рисунок 12).
Рисунок 12 – Шаг 1 решения системы линейных уравнений
Для решения системы методом обратной матрицы необходимо вычислить матрицу, обратную к A . Для этого определим ячейки для хранения обратной матрицы, пусть это будут ячейки B6:E9.
Обратимся к мастеру функций, и выберем функцию МОБР , щелкнув по кнопке OK, перейдём ко второму шагу мастера функций. В диалоговом окне, появляющемся на следующем шаге мастера функций, необходимо заполнить поле ввода Массив . Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица — в нашем случае B1:E4. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.
Если поле Массив заполнено, нажать кнопку OK. В первой ячейке, выделенного под обратную матрицу диапазона, появится некое число. Для того чтобы получить всю обратную матрицу, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter. Рабочий лист Excel примет вид, изображенный на рисунке 13.
Р
исунок 13 – Шаг 2 решения системы линейных уравнений
Теперь необходимо умножить полученную обратную матрицу на вектор b . Выделим ячейки для хранения результирующего вектора, например H6:H9. Обратимся к мастеру функций, и выберем функцию МУМНОЖ , предназначенную для умножения матриц. На втором шаге мастера функций в диалоговом окне введем в поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B6:E9 (обратная матрица), а в поле Массив2 ячейки, содержащие вторую матрицу, в нашем случае G1:G4 (вектор b ).
Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор х и получить в результате вектор b . Умножение матрицы A на вектор x осуществляется при помощи функции = МУМНОЖ (В1:Е4;Н6:Н9), так как было описанной выше.
В
результате проведенных вычислений рабочий лист примет вид изображенный на рисунке 13.
Рисунок 13 – Шаг 3 решения системы линейных уравнений матричным методом
Решим пример методом Крамера.
Введём матрицу А и вектор b на рабочий лист. Сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b (рисунок 14).
Для дальнейшего решения необходимо вычислить определитель матрицы A. Установим курсор в ячейку I10 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД, предназначенную для вычисления определителя матрицы, и перейдём ко второму шагу мастера функций. Диалоговое окно, появляющееся на втором шаге содержит поле ввода Массив. В этом поле указывают диапазон матрицы, определитель которой вычисляют. В нашем случае это ячейки B1:E4.
Для вычисления вспомогательных определителей введем формулы:
I12= МОПРЕД (B11:E14) ,
I13= МОПРЕД (B16:E19),
I14= МОПРЕД (B21:E24) .
В результате в ячейке I10 хранится главный определитель, а в ячейках I11:I14 — вспомогательные.
Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный. В ячейку K11 введём формулу=I11/$I$10. Затем скопируем её содержимое в ячейки K12, K13 и K14. Система решена.
Рисунок 14 — Решения системы линейных уравнений методом Крамера
2. Решить системы уравнений согласно вариантам с помощью обратной матрицы и методом Крамера.
При решении систем обязательно выполнить проверку.
Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7 Вариант 8 Вариант 9 Вариант 10 Вариант 11 Вариант 12 Вариант 13 Вариант 14 Вариант 15 Вариант 16 Вариант 17 Вариант 18 Вариант 19 Вариант 20
Обратите внимание на особенность работы с матричными формулами: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ — Тема: Решение систем линейных уравнений приближёнными методами.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО
Разработал преподаватель: Игнатьева Елена Сергеевна
Решение систем линейных уравнений приближёнными методами.
— применить теоретический материал по данной теме через решение упражнений;
— применить умения решать системы линейных уравнений методом Гаусса, методом Зейделя и простой итерации;
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
1. Решить систему линейных уравнений методом Гаусса.
2. Решить систему линейных алгебраических уравнений методом Зейделя и простой итерации.
1. Решить систему линейных уравнений методом Гаусса.
2. Решить систему линейных алгебраических уравнений методом Зейделя и простой итерации.
1. Внимательно прочитать тему и цель практической работы .
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Пусть требуется решить систему n линейных алгебраических уравнений с n неизвестными:
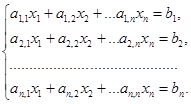
Прямой ход метода Гаусса преобразует систему (1) к треугольному виду исключением соответствующих неизвестных. Пусть 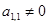
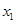
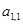
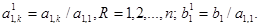
Затем от второго уравнения отнимаем первое уравнение, умноженное на 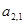
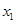
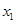
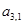
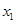
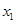
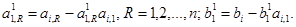
В результате этих вычислений получим систему вида
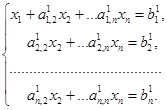
На втором шаге исключаем переменную 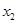
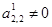
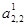
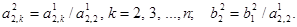
В системе (3.12) с помощью второй строки исключим 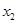
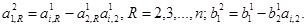
Система (3.12) преобразуется к следующему виду:
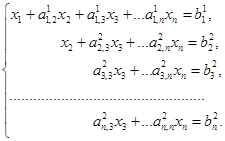
1. В общем случае на шаге m для 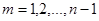
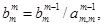
а затем исключаем переменную 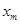
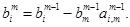
Здесь предполагается, что на каждом шаге выполняется условие
В результате 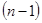
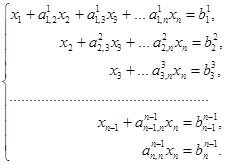
2. Обратный ход метода Гаусса вычисляет неизвестные 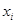
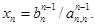
Неизвестные 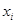
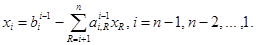
Метод Гаусса предполагает, что на m — м шаге выполняется условие 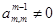
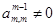
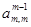
Чтобы избежать этих трудностей, применяют метод Гаусса с выбором главного элемента. Одним из вариантов этого метода является метод Гаусса с выбором главного элемента по столбцам. В качестве ведущего элемента на каждом шаге выбирают наибольший по модулю элемент столбца и переставляют соответствующую строку с другой строкой так, чтобы найденный элемент стал диагональным, затем исключают соответствующую переменную. Так как при этих перестановках переменные в уравнениях остаются на своих местах, решение преобразованной системы совпадает с решением исходной системы уравнений.
Метод Гаусса с выбором главного элемента по столбцам отличается от алгоритма (8)-(12) только тем, что перед преобразованием (8) нужно выполнить поиск максимального по модулю элемента в m — м столбце и переставить строки системы уравнений так, чтобы максимальный элемент стал диагональным элементом матрицы коэффициентов.
Алгоритм метода Гаусса с выбором главного элемента по столбцам:
1. Для 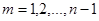
Найдём Максимальный по абсолютной величине элемент в m -м столбце. Пусть это будет элемент 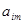
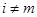
Элементы матрицы и вектора после преобразования на m -м шаге обозначим 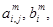
Делим m -е уравнение на ведущий элемент 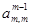
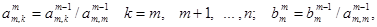
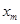
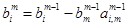
2. Вычисляем неизвестные 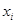
Приведённый вариант метода Гаусса даёт решение и тогда, когда обычный метод Гаусса перестаёт работать из за деления на 0.
При реализации метода Гаусса на каком-либо языке программирования удобно использовать исходные матрицу a и вектор b для хранения промежуточных результатов преобразований. Приведённые формулы преобразований записываются как операторы присваивания, т.е. имена переменных 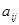
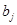
В методе Гаусса с выбором главного элемента по строкам на каждом шаге выбирают наибольший по модулю элемент строки и переставляют столбцы так, чтобы ведущий элемент находился на диагонали. В этом варианте в уравнениях неизвестные переменные меняются местами и в алгоритме необходимо думать о том, чтобы запомнить эти перестановки.
В общем случае метода Гаусса с выбором главного элемента на шаге m ищется максимальный по модулю элемент во всей матрице коэффициентов и производится перестановка строк и столбцов так, чтобы этот элемент стал диагональным.
Мы не будем рассматривать реализации указанных вариантов метода Гаусса. Отметим, что последний вариант с выбором главного элемента считался лучшим.
Общее число операций для решения системы уравнений методом Гаусса составляет приблизительно 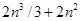
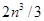
Запишем систему уравнений в виде:
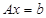
где A – матрица коэффициентов; b – вектор правовых частей системы.
Преобразуем (1) к виду, удобному для интеракций:
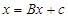
Тогда метод простой итерации определяется формулой:
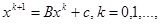
Где начальное приближение 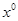
В качестве критерия сходимости метода итераций обычно применяют условие
Сформулируем теоремы об условиях сходимости метода простых итераций.
Теорема 1. (достаточное условие сходимости). Если 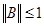
Теорема 2. (необходимое и достаточное условие сходимости). Пусть система (14) имеет единственное решение. Итерационный процесс (15) сходится к решению системы (14) тогда и только тогда, когда все собственные значения матрицы. B по модулю меньше единицы.
Теоремы 1 и 2 не дают способов преобразования произвольной системы линейных уравнений к виду (14) так, чтобы метод итераций (15) при этом сходился к решению. Эти теоремы имеют важное теоретическое значение. Отметим, что на практике для проверки условия сходимости метода итераций более полезна теорема 1, а теорему 2 удается использовать тогда, когда собственные значения матрицы B известны. Задача определения собственных значений матрицы в общем случае сложнее, чем задача решения системы линейных уравнений.
Для преобразования системы уравнений к виду, удобному для итераций, можно умножить систему (13) на матрицу 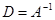
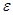
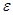
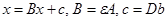
и матрица B будет удовлетворять теореме 1, если выбрать элементы матрицы e достаточно малыми по модулю. Однако этот прием не выгоден, так как для вычисления обратной матрицы 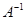
При небольшом числе уравнений систему иногда удается привести к виду, удобному для итераций, с помощью нескольких преобразований.
Далее будут рассмотрены разностные методы решения краевых задач для обыкновенных дифференциальных уравнений и уравнений в частных производных, которые приводят к решению систем линейных уравнений с большим числом известных. Учитывая специфику таких систем, часто удается построить эффективные итерационные методы решения.
Пусть требуется решить систему уравнений
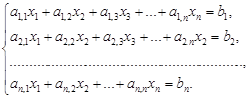
Выразим из первого уравнения переменную 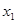
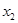
Пусть k — e приближение к решению обозначен как 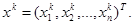
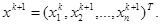
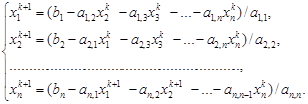
Теорема 3. (достаточные условия сходимости)
Пусть при всех i для коэффициентов системы уравнений выполняются условия
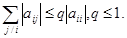
Тогда метод Зейделя сходится и выполняется неравенство
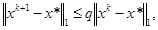
Где x * — точное решение системы (5)
Если матрица А удовлетворяет условию (19), говорят, что А – матрица с диагональным преобладанием.
При выполнении практической работы рассмотрите следующие примеры:
Решение систем методом Гаусса с выбором главного элемента по столбцу. Пусть Ax = b , где
Вычислим масштабирующие множители 1 шага:
И выполним преобразование матрицы и вектора:
2 шаг. Вычислим масштабирующие множители 2 шага:
3 шаг. Максимальный по модулю элемент 3 столбец 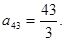
Вычислим масштабирующие множители 3 шага:
И выполним преобразование матрицы и вектора:
Обратный ход. Из последнего уравнения находим: 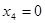
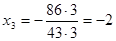
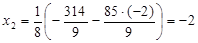
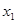
Ответ: 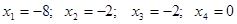
Решить систему линейных алгебраических уравнений методом простой итерации:
Решение. Здесь модули коэффициентов 10, 5 и 4 системы значительно преобладают над остальными коэффициентами при неизвестных.
Приведем систему к нормальному виду:
В качестве нулевых приближений принимаем значения:
Подставляя эти значения в правые части системы получим первые приближения
Полученные значения 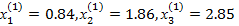
Методом Зейделя решить систему уравнений
Решение. Преобразуем систему к виду, удобному для итераций.
Меняем местами в системе уравнения так, чтобы наибольший по модулю коэффициент уравнения оказался диагональным
Т.к. для сходимости процесса Зейделя, модуль коэффициента, стоящего на главной диагонали, должен быть больше суммы модулей других коэффициентов. В преобразованной системе это условие выполняется.
Замечание. В тех случаях, когда это условие в исходной системе не выполняется, необходимо вместо отдельных уравнений данной системы записывать их удачные линейные комбинации, позволяющие получить нужный результат.
Приведем систему к нормальному виду с помощью следующих преобразований:
Деля все уравнения системы на десять, получим систему уравнений, эквивалентную исходной и удовлетворяющую условию сходимости процесса Зейделя:
В качестве нулевых приближений принимаем значения:
Подставляя эти значения в правые части системы получим первые приближения
Полученные значения 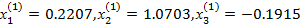
Вопросы для закрепления теоретического материала к практическому занятию:
1. В чем заключается суть метода Гаусса?
2. В чем суть решения линейных уравнений методом интеграции?
3. В чем суть решения линейных уравнений методом Зейделя?
Название практической работы.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
— Численные методы и программирование: Учебное пособие / В.Д. Колдаев; Под ред. Л.Г. Гагариной. — М.: ИД ФОРУМ: НИЦ Инфра-М, 2016. — 336 с…
— Гателюк, О. В. Численные методы : учеб. пособие для СПО / О. В. Гателюк, Ш. К. Исмаилов, Н. В. Манюкова. — М. : Издательство Юрайт, 2018. — 140 с. — (Серия : Профессиональное образование)
— Бахвалов Н.С., Лапин А.В., Чижонков Е.В. «Численные методы в задачах и упражнениях»/ Под ред. В.А.Садовничего – М.:Высш.шк.,2016
— Вержбицкий В.М. «Численные методы. Математический анализ и обыкновенные дифференциальные уравнения» — М.: Высшая школа, 2017
— Волков Е.А. «Численные методы» — СПб.: Издательство «Лань», 2015
— Исаков В.Н. «Элементы численных методов» — М.: Издательский центр «Академия», 2016.
Решение систем линейных алгебраических уравнений
Страницы работы
Содержание работы
Лабораторная работа №3
Решение систем линейных алгебраических уравнений
Практика использования итерационных методов решения системы линейных алгебраических уравнений. Сравнительный анализ методов.
Решить систему линейных алгебраических уравнений (САУ)
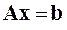
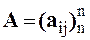
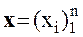
итерационными методами Зейделя и наискорейшего спуска с точностью до e = 0,001. Для сравнения с истинными значениями корней выполнить решение указанной САУ методом Гаусса.
Общий вид алгоритма Зейделя и наискорейшего спуска
Метод Зейделя заключается в том, что найденное на 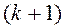
Расчетные соотношения метода Зейделя для подготовленной системы уравнений (4.13) имеют вид
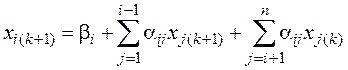
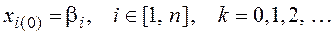
При составлении программы для вычислений на ЭВМ вместо соотношения (4.18) удобнее использовать выражение, в котором фигурируют элементы исходной системы уравнений
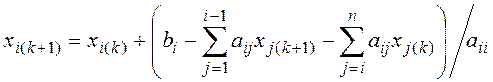
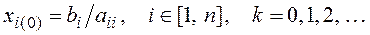
Если матрица 
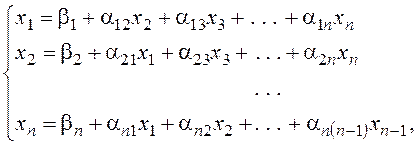
где 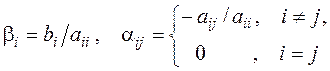


Из неособенной матрицы 

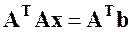
Метод наискорейшего спуска. Данный метод относится к группе нелинейных градиентных алгоритмов. Градиентные алгоритмы, уточнение решения в которых осуществлялось по отдельным координатам, предполагают траекторию движения к истинному решению сразу по всем координатам по линии наискорейшего спуска в направлении, противоположном вектору градиента функционала, связанного с ошибкой между истинным решением и решением на 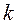
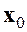
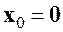
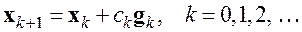
где 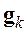
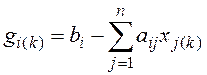
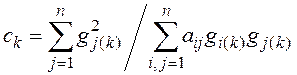
Чтобы упростить процедуру определения вектора невязки, особенно при больших порядках 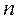
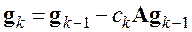
Однако из-за наличия вычислительных погрешностей векторы 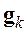
Если матрица 
SUBROUTINE N1YMGS (A,B,N,G,X),
SUBROUTINE N1YMNS (A,B,N,G,X)
реализуют алгоритмы решения САУ методами Зейделя и наискорейшего спуска (одна итерация) соответственно.
Входные параметры подпрограмм:
А(N,N) — (N ´ N)-мерная матрица САУ;
B(N) — N-мерный вектор правой части САУ;
N — мерность САУ;
G(N) — N-мерный вектор невязки (g = b — Ax);
X(N) — N-мерный вектор начальных условий решения САУ.
Выходные параметры подпрограммы:
X(N) — N-мерный вектор уточненных значений решения САУ.
Окончание итерационной процедуры производиться при выполнении условия 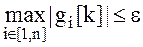
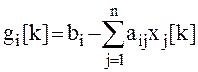
SUBROUTINE N1YGAU (A,B,X,N)
реализует алгоритм метода Гаусса с выбором главного элемента.
Входные A, B, N и выходной X параметры подпрограммы N1YGAU совпадают по описанию с аналогичными параметрами в подпрограммах N1YMGS, N1YMNS.
В подпрограмме N1YGAU матрица A приводится к треугольной.
http://znanio.ru/media/metodicheskie-ukazaniya-po-vypolneniyu-prakticheskoj-raboty-po-chislennym-metodam-tema-reshenie-sistem-linejnyh-uravnenij-priblizhyonnymi-metodami-2568014
http://vunivere.ru/work36005