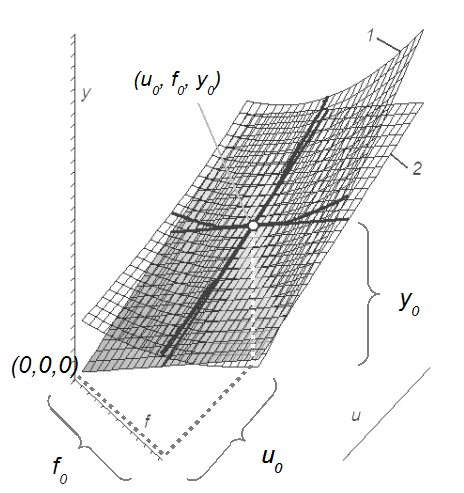
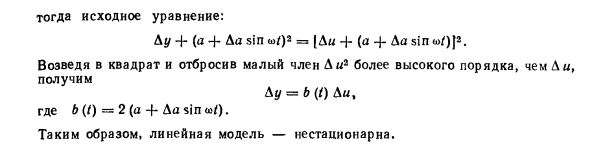Линеаризация моделей статики.
Читайте также:
|
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- В частности, система стабилизации принимает определенное постоянное значение. Однако, поскольку фактический режим отличается от требуемого (заданного) режима из-за различных возмущающих факторов, текущие значения входных и выходных величин не равны значениям, соответствующим указанному режиму. В функционирующей системе аутизма фактический режим немного отличается от требуемого режима, и отклонение входных и выходных значений строительного блока от требуемых значений является небольшим. Это позволяет линеаризовать путем разложения нелинейной функции уравнения в ряд Тейлора.
Пример 2.1. Выше поясняется на примере ссылки, описанной в уравнении (2.1). Соответствовать указанному режиму и = и *, и = и *; / = / ! / = (/ ‘, Y = Y *, y ** y *. (2.3) Указывает отклонение фактических значений u, / и y от значений, требуемых для Dm, D / и Lu, т. Е. A и -u-u *, Af = f- / *, Ay = y-y *. Тогда u = u * 4-Aw, u = m * + Au, f = f * + D /, y = y * + Au, Y-y * + A
Линеаризация может быть выполнена по ссылкам. Людмила Фирмаль
Уравнение (2.5) было получено при следующих допущениях: Функция F имеет непрерывные частные производные по всем аргументам вблизи точки, соответствующей данной моде. Если хотя бы одно из этих условий не выполняется, линеаризация не может быть выполнена. Для первого условия вы должны знать следующее: Невозможно уменьшить все отклонения одновременно. Это зависит от типа нелинейности. Во многих случаях нелинейные отношения между отдельными переменными в уравнении связи задаются в форме кривой. В этих случаях линеаризация может быть выполнена графически.
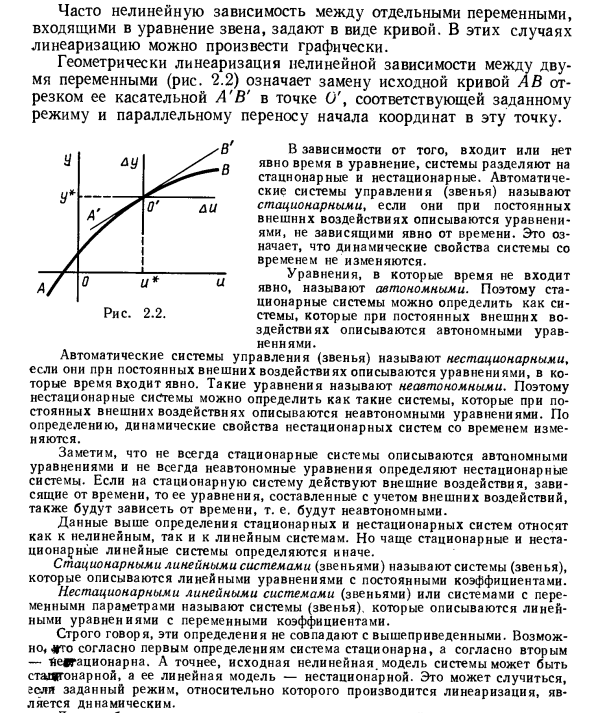
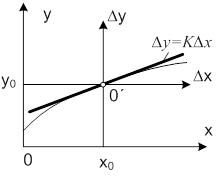
Геометрическая линеаризация нелинейной зависимости между двумя переменными (рис. 2.2) должна заменить исходную кривую A этого касательного сегмента A’B, соответствующего конкретной моде, и этой точке Это означает перевод происхождения. Рисунок 2.2. В зависимости от того, явно ли время входит в уравнение, система делится на стационарную и нестационарную. Автоматическая система управления (ссылка) называется стационарной, когда она описывается явным не зависящим от времени уравнением при определенных внешних воздействиях.
Это означает, что динамические свойства системы не меняются со временем. Уравнение, которое явно не включает время, называется автономией. Таким образом, стационарная система может быть определена как система, описываемая автономными уравнениями при определенных внешних воздействиях. Автоматическая система управления (ссылка) называется неустановившейся, если она описывается уравнением, в которое время вводится явно при определенных внешних воздействиях. Такое уравнение называется неавтономным. Таким образом, нестационарная система может быть определена как система, описываемая неавтономным уравнением при определенных внешних воздействиях.
По определению динамические характеристики нестационарных систем меняются со временем. Обратите внимание, что стационарные системы не всегда описываются автономными уравнениями, а неавтономные уравнения не всегда определяют нестационарные системы. Если зависящие от времени внешние эффекты действуют на стационарную систему, уравнения, составленные для внешних воздействий, также зависят от времени. То есть они не автономны. Приведенные выше определения стационарных и нестационарных систем относятся как к нелинейным, так и к линейным системам. Однако чаще определение фиксированных и нефиксированных линейных систем различается. Стационарная линейная система (звено) называется системой (звено) и описывается линейным уравнением с постоянными коэффициентами.
Переходные линейные системы (звенья) или системы с переменными параметрами называются системами (звеньями) и описываются линейными уравнениями с переменными коэффициентами. Строго говоря, эти определения не соответствуют вышеприведенному. Возможно, согласно первому определению, 4го является стационарной системой, а согласно второму определению яйцо является стационарным. Точнее, исходная нелинейная модель системы статзонарна, а ее линейная модель нестационарна. Это может произойти, и режим спецификации геля, связанный с выполнением линеаризации, является динамическим. Кроме того, следует второе определение. Первый может быть связан только с нелинейными системами.
Пример 2.2 Напишите статическую нелинейную статическую связь с уравнением y = / A. Линеаризовать относительно данного режима И * = a 4-да, грех y * = (a-J-да, грех W) 2. Об отклонении Lj / = y / -y * -y- (a H-yes sin w /) 2, Di-u-u * = u- (a-f-Yes sin w /), Исходное уравнение: & Y + (a-f sin®> /) 2 = [yes-f (a-fyessin (OD «, Где b (/) = 2 (a-f yes sinoo /). Таким образом, линейная модель является переходной.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Линеаризация статических характеристик звеньев
Статическая характеристика звена описывает соотношение между входной и выходной величинами в статике (установившемся режиме). Статические характеристики могут быть заданы графически и аналитически. При наличии статических характеристик звеньев можно построить статические характеристики группы звеньев, а также характеристики всей системы.
Замена реальных нелинейных характеристик линейными называется линеаризацией.
Пусть имеем нелинейное звено (рис. 1.17).
Рис. 1.17 Рис. 1.18
Статическая характеристика звена описывается функцией 


Если функция в окрестности x 0 1 непрерывна и дифференцируема, то ее можно разложить в ряд Тейлора

Через 

Обычно считают, что члены высшего порядка малости много меньше двух первых слагаемых, потому ими пренебрегают

Вычтем из (2.3) уравнение (2.1) почленно и получим
|

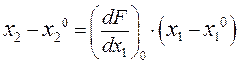

где 
Уравнение (2.4) называется уравнением в отклонениях и соответствует статике звена.
Практически линеаризацию проводят чаще всего путем проведения касательной в точке установившегося режима и определяют 

Линеаризация нелинейных дифференциальных уравнений.
Чаще всего процессы в звеньях описываются нелинейными дифференциальными уравнениями.
Рассмотрим процесс линеаризации на примере дифференциального уравнения второго порядка

где 



Пусть в установившемся режиме звена справедливо



Тогда уравнение установившегося режима примет вид

Разложим (2.5) в ряд Тейлора в точке установившегося режима, рассматривая (2.5) как функцию от независимых переменных,

где 



Вычтем из (2.7) уравнение (2.6) и положим Q =0, тогда получим уравнение в отклонениях:






Уравнение (2.8) описывает тот же процесс, что и (2.5), но имеет отличия:
· Уравнение (2.8) является линейным относительно переменных 

· Вместо 



· Уравнение (2.8) является приближенным.
Безразмерная форма записи уравнений
Введем относительные переменные:


Подставим (2.9) в (2.8)

Разделим (2.10) на 






Уравнение (2.11) можно преобразовать

где 


Решая уравнение (2.12) как линейное, можно получить закон изменения выходной величины 


Пример линеаризации звена.
Дана нелинейная функция 
Образуем функцию 
Разложим функцию в ряд Тейлора


Откуда получим уравнение в отклонениях

ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ СИСТЕМЫ
Динамическое звено – это устройство любого вида и принципа действия, описываемое определенным дифференциальным уравнением. Свойства звена могут быть определены различными характеристиками: передаточной функцией, временными характеристиками и частотными характеристиками.
Передаточная функция звена
Пусть дано динамическое звено.
 | |
|
Дифференциальное уравнение такого звена можно записать следующим образом:

Применим преобразование Лапласа, тогда уравнение (3.1) можно записать:

Правила преобразования Лапласа для производных:
Если 



Тогда в уравнении (3.2)



Из уравнения (3.2) выразим

Первая составляющая представляет собой эффект действия входного сигнала на звено. Вторая составляющая учитывает начальные условия входной и выходной величин.
Пусть при 


Тогда 



Выражение (3.5) называется передаточной функцией звена.
Таким образом, передаточной функцией звена (или системы) называется отношение изображений выходной и входной величин при нулевых начальных условиях.
С физической точки зрения 
Выражение (3.5) можно представить графически (рис. 3.2).
http://lfirmal.com/uravneniya-dinamiki-i-statiki-linearizaciya/
http://zdamsam.ru/a31700.html

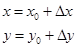
 .
.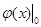 означает, что значение функции
означает, что значение функции  вычисляется в точке
вычисляется в точке  .
. , где
, где 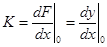 .
.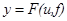

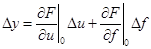 (2)
(2)