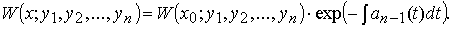Линейно независимые решения дифференциальных уравнений

Линейно независимые решения дифференциальных уравнений

ЛИНЕЙНАЯ НЕЗАВИСМОСТЬ РЕШЕНИЙ ЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Высшая математика

Рассмотрим линейное однородное дифференциальное уравнение

Справедливо следующее этого уравнения.

Решения y ₁( x ), y ₂( x ), . y _n( x ) линейного однородного дифференциального уравнения линейно независимы на отрезке [ a ; b ] тогда и только тогда, когда определитель Вронского этих функций W ( x ; y ₁( x ), y ₂( x ), . y _n( x )) не обращается в нуль ни в одной точке отрезка [ a ; b ] .

Для определителя Вронского W ( x ; y ₁( x ), y ₂( x ), . y _n( x )) решений y ₁( x ), y ₂( x ), . y _n( x ) линейного однородного дифференциального уравнения с непрерывными на [ a ; b ] коэффициентами, справедлива формула Остроградского–Лиувилля:

Из формулы Остроградского-Лиувилля, в частности, следует:

Линейная независимость функций. Определители Вронского и Грама

Пусть имеем конечную систему из функций , определенных на интервале . Функции называют линейно зависимыми на интервале , если существуют постоянные , не все равные нулю, такие, что для всех значений из этого интервала справедливо тождество

Если же это тождество выполняется только при , то функции называют линейно независимыми на интервале .

Пример 1. Показать, что система функций линейно независима на интервале .

Решение. В самом деле, равенство может выполняться для всех только при условии, что . Если же хоть одно из этих чисел не равно нулю, то в левой части равенства будем иметь многочлен степени не выше третьей, а он может обратиться в ноль не более, чем при трех значениях из данного интервала.

Пример 2. Показать, что система функций , где попарно различны, линейно независима на интервале .

Решение. Предположим обратное, т. е. что данная система функций линейно зависима на этом интервале. Тогда

на интервале , причем, по крайней мере, одно из чисел отлично от нуля, например . Деля обе части тождества (1) на , будем иметь

Дифференцируя тождество, получаем

Делим обе части тождества (2) на :

Дифференцируя (3), получаем , что невозможно, так как по предположению, по условию, а .

Наше предположение о линейной зависимости данной системы функций привело к противоречию, следовательно, эта система функций линейно независима на интервале , т.е. тождество (1) будет выполняться только при .

Пример 3. Показать, что система функций , где , линейно независима на интервале .

Решение. Определим значения и , при которых будет выполняться тождество

Разделим обе его части на :

Подставляя в (5) значение , получаем и, значит, ; но функция не равна тождественно нулю, поэтому . Тождество (5) и, следовательно, (4) имеют место только при , т. е. данные функции линейно независимы в интервале .

Замечание. Попутно доказана линейная независимость тригонометрических функций .

Пример 4. Доказать, что функции

линейно зависимы в интервале .

Решение. Покажем, что существуют такие числа , не все равные нулю, что в интервале справедливо тождество

Предполагаем тождество (7) выполненным; положим, например, . Тогда получим однородную систему трех уравнений с тремя неизвестными

Определитель этой системы трёх уравнений с тремя неизвестными равен нулю:

Следовательно, однородная система (8) имеет ненулевые решения, т. е. существуют числа , среди которых имеется по крайней мере одно отличное от нуля. Для нахождения такой тройки чисел возьмем, например, два первых уравнения системы (8):

Из первого уравнения имеем , из второго . Полагая , получим ненулевое решение системы (8):

Покажем теперь, что при этих значениях тождество (7) будет выполняться для всех . Имеем

каково бы ни было . Следовательно, система функций (6) линейно зависима на интервале .

Замечание. Для случая двух функций можно дать более простой критерий линейной независимости. Именно, функции и будут линейно независимыми на интервале , если их отношение не равно тождественной постоянной на этом интервале; если же , то функции будут линейно зависимыми.

Пример 5. Функции и линейно независимы в интервале , так как их отношение в этом интервале.

Пример 6. Функции и линейно зависимы в интервале , так как их отношение в этом интервале (в точках разрыва функции доопределяем это отношение по непрерывности).

Пусть функций имеют производные (n–1)-го порядка. Определитель

называется определителем Вронского для этой системы функций. Определитель Вронского вообще является функцией от , определенной в некотором интервале.

Пример 7. Найти определитель Вронского для функций .

Пример 8. Найти определитель Вронского для функций:

так как первая и последняя строки определителя пропорциональны.

Теорема. Если система функций линейно зависима на отрезке , то ее определитель Вронского тождественно равен нулю на этом отрезке.

Так, например, система функций линейно зависима в интервале , и определитель Вронского этих функций равен нулю всюду в этом интервале (см. примеры 4 и 8).

Эта теорема дает необходимое условие линейной зависимости системы функций. Обратное утверждение неверно, т. е. определитель Вронского может тождественно обращаться в ноль и в том случае, когда данные функции образуют линейно независимую систему на некотором интервале.

Пример 9. Рассмотрим две функции:

Графики их имеют вид, указанный на рис. 25.

Эта система функций линейно независима, так как тождество выполняется только при . В самом деле, рассматривая его на отрезке , мы получаем , откуда , так как ; на отрезке же имеем , откуда , так как на этом отрезке.

Найдем определитель Вронского системы. На отрезках и :

Таким образом, определитель Вронского на отрезке тождественно равен нулю.

Пусть имеем систему функций на отрезке . Положим

называется определителем Грама системы функций .

Теорема. Для того, чтобы система функций была линейно зависимой, необходимо и достаточно, чтобы ее определитель Грама равнялся нулю.

Пример 10. Показать, что функции и линейно зависимы на отрезке .

Вычислим определитель Грама следовательно, функции и линейно зависимы.

Линейные дифференциальные уравнения высших порядков

Оговорим сразу тот факт, что нахождение решения общего аналитического вида для линейных однородных и неоднородных дифференциальных уравнений высших порядков зачастую невозможно. В основном пользуются приближенными методами решения.

Материал данной статьи представлен базовой теоретической информацией на тему решения ЛОДУ
n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 и ЛНДУ n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) .

Сначала поговорим о линейных однородных дифференциальных уравнениях n -ого порядка, а затем займемся неоднородными ДУ.

Линейные однородные дифференциальные уравнения

Общее решение для линейного однородного дифференциального уравнения n -ого порядка y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 при непрерывных на интервале интегрирования
X коэффициентах f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) определяет линейная комбинация y 0 = ∑ j = 1 n C j · y j , в которой y j , j = 1 , 2 , . . . , n являются линейно независимыми частными решениями ЛОДУ на X , а C j , j = 1 , 2 , . . . , n являются произвольными постоянными.

Когда тождество a 1 · y 1 + a 2 · y 2 + . . . + a n · y n ≡ 0 верно только при нулевых коэффициентах a 1 = a 2 = . . . = a n = 0 , функции y j , j = 1 , 2 , . . . , n являются линейно независимыми на неком интервале X .

Для линейно независимых функций y j , j = 1 , 2 , . . . , n определитель Вронского при любых
x из X отличен от нуля:

W ( x ) = y 1 y 2 … y n y ‘ 1 y ‘ 2 … y ‘ n y » 1 y » 2 … y » n … … … … y 1 ( n — 1 ) y 2 ( n — 1 ) … y n ( n — 1 ) ≠ 0

Тот факт, что определитель Вронского не равен нулю, возможно применять в качестве критерия линейной независимости функций на интервале.

Каким же образом определяются y j , j = 1 , 2 , . . . , n — линейно независимые частные решения линейного однородного дифференциального уравнения n -ого порядка?

В большинстве случаев данные функции возможно подобрать, используя стандартные системы линейно независимых функций:

1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 · x , e k 2 · x , . . . , e k n · x 3 ) e k 1 · x , x · e k 1 · x , . . . , x n 1 · e k 1 · x , e k 2 · x , x · e k 2 · x , . . . , x n 2 · e k 2 · x , . . . e k p · x , x · e k p · x , . . . , x n p · e k p · x

Когда подобраны все n линейно независимые частные решения y j , j = 1 , 2 , . . . , n , возможно составить общее решение линейного однородного дифференциального уравнения n -ого порядка y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 — оно будет иметь запись y 0 = ∑ j = 1 n C j · y j . Когда подобраны только несколько линейно независимых частных решений, мы можем понизить степень заданного уравнения при помощи замены. Детально этот пункт мы не будем рассматривать, в случае необходимости следует изучить дополнительные материалы по теме.

Линейные неоднородные дифференциальные уравнения

Приступим к рассмотрению линейных неоднородных дифференциальных уравнений n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) .

Общее решение на интервале X линейного неоднородного дифференциального уравнения порядка n записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) при непрерывных на интервале интегрирования X коэффициентах f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) и непрерывной функции f ( x ) определяется как сумма общего решения y 0 соответствующего ЛОДУ и некоторого частного решения y

заданного неоднородного уравнения: y = y 0 + y

Нахождение y 0 — общего решения соответствующего ЛОДУ n -ого порядка — было рассмотрено выше. Остается разобрать, как находится y

— частное решение линейного неоднородного дифференциального уравнения n -ого порядка.

Иногда некое частное решение y

бывает достаточно явным, то есть его возможно подобрать. Когда
y

подобрать затруднительно, при этом определены n линейно независимых частных решений y j , j = 1 , 2 , . . . , n соответствующего ЛОДУ, общее решение исходного ЛНДУ n -ого порядка возможно определить при помощи метода вариации произвольных постоянных.

В таком случае общее решение линейного неоднородного дифференциального уравнения y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) определяется как y = ∑ j = 1 n C j ( x ) · y j , а функции C 1 ( x ) , C 2 ( x ) , … , C n ( x ) находятся интегрированием после решения системы уравнений:

∑ j = 1 n C j ‘ ( x ) · y j = 0 ∑ j = 1 n C j ‘ ( x ) · y ‘ j = 0 ∑ j = 1 n C j ‘ ( x ) · y » j = 0 … ∑ j = 1 n C j ‘ ( x ) · y j ( n — 2 ) = 0 ∑ j = 1 n C j ‘ ( x ) · y j ( n — 1 ) = 0