Линейно зависимая система уравнений это

Линейная зависимость системы векторов. Коллинеарные векторы

В данной статье мы расскажем:

• что такое коллинеарные векторы;
• какие существуют условия коллинеарности векторов;
• какие существуют свойства коллинеарных векторов;
• что такое линейная зависимость коллинеарных векторов.

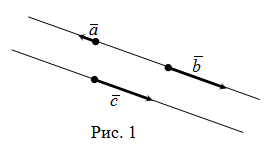
Коллинеарные векторы

Коллинеарные векторы — это векторы, которые являются параллелями одной прямой или лежат на одной прямой.

Условия коллинеарности векторов

Два векторы являются коллинеарными, если выполняется любое из следующих условий:

• условие 1. Векторы a и b коллинеарны при наличии такого числа λ , что a = λ b ;
• условие 2. Векторы a и b коллинеарны при равном отношении координат:

a = ( a 1 ; a 2 ) , b = ( b 1 ; b 2 ) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• условие 3. Векторы a и b коллинеарны при условии равенства векторного произведения и нулевого вектора:

Условие 2 неприменимо, если одна из координат вектора равна нулю.

Условие 3 применимо только к тем векторам, которые заданы в пространстве.

Примеры задач на исследование коллинеарности векторов

Исследуем векторы а = ( 1 ; 3 ) и b = ( 2 ; 1 ) на коллинеарность.

В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:

Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.

Ответ: a | | b

Какое значение m вектора a = ( 1 ; 2 ) и b = ( — 1 ; m ) необходимо для коллинеарности векторов?

Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:

Отсюда видно, что m = — 2 .

Ответ: m = — 2 .

Критерии линейной зависимости и линейной независимости систем векторов

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

Пусть система e 1 , e 2 , . . . , e n является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Пусть a k ≠ 0 k ∈ 1 , 2 , . . . , n .

Делим обе части равенства на ненулевой коэффициент:

a k — 1 ( a k — 1 a 1 ) e 1 + ( a k — 1 a k ) e k + . . . + ( a k — 1 a n ) e n = 0

— a k — 1 a m , где m ∈ 1 , 2 , . . . , k — 1 , k + 1 , n

β 1 e 1 + . . . + β k — 1 e k — 1 + β k + 1 e k + 1 + . . . + β n e n = 0

или e k = ( — β 1 ) e 1 + . . . + ( — β k — 1 ) e k — 1 + ( — β k + 1 ) e k + 1 + . . . + ( — β n ) e n

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

Пусть один из векторов можно линейно выразить через все остальные векторы системы:

e k = γ 1 e 1 + . . . + γ k — 1 e k — 1 + γ k + 1 e k + 1 + . . . + γ n e n

Переносим вектор e k в правую часть этого равенства:

0 = γ 1 e 1 + . . . + γ k — 1 e k — 1 — e k + γ k + 1 e k + 1 + . . . + γ n e n

Поскольку коэффициент вектора e k равен — 1 ≠ 0 , у нас получается нетривиальное представление нуля системой векторов e 1 , e 2 , . . . , e n , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).

• Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
• Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.

Свойства линейно зависимых векторов

1. Для 2-х и 3-х мерных векторов выполняется условие: два линейно зависимых вектора — коллинеарны. Два коллинеарных вектора — линейно зависимы.
2. Для 3-х мерных векторов выполняется условие: три линейно зависимые вектора — компланарны. (3 компланарных вектора — линейно зависимы).
3. Для n-мерных векторов выполняется условие: n + 1 вектор всегда линейно зависимы.

Примеры решения задач на линейную зависимость или линейную независимость векторов

Проверим векторы a = 3 , 4 , 5 , b = — 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 на линейную независимость.

Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.

Проверим векторы a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , — 1 , 1 на линейную независимость.

Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:

x 1 a + x 2 b + x 3 c 1 = 0

Записываем векторное уравнение в виде линейного:

x 1 + x 2 = 0 x 1 + 2 x 2 — x 3 = 0 x 1 + x 3 = 0

Решаем эту систему при помощи метода Гаусса:

1 1 0 | 0 1 2 — 1 | 0 1 0 1 | 0

Из 2-ой строки вычитаем 1-ю, из 3-ей — 1-ю:

1 1 0 | 0 1 — 1 2 — 1 — 1 — 0 | 0 — 0 1 — 1 0 — 1 1 — 0 | 0 — 0

1 1 0 | 0 0 1 — 1 | 0 0 — 1 1 | 0

Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:

1 — 0 1 — 1 0 — ( — 1 ) | 0 — 0 0 1 — 1 | 0 0 + 0 — 1 + 1 1 + ( — 1 ) | 0 + 0

0 1 0 | 1 0 1 — 1 | 0 0 0 0 | 0

Из решения следует, что у системы множество решений. Это значит, что существует ненулевая комбинация значения таких чисел x 1 , x 2 , x 3 , при которых линейная комбинация a , b , c равняется нулевому вектору. Следовательно, векторы a , b , c являются линейно зависимыми. ​​​​​​​

Линейная зависимость и независимость векторов

Набор векторов называется системой векторов .

Система из векторов называется линейно зависимой , если существуют такие числа , не все равные нулю одновременно, что

Система из векторов называется линейно независимой, если равенство (1.1) возможно только при , т.е. когда линейная комбинация в левой части равенства (1.1) тривиальная.

1. Один вектор тоже образует систему: при — линейно зависимую, а при — линейно независимую.

2. Любая часть системы векторов называется подсистемой .

Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора , то она линейно зависима.

4. Система из 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQCAMAAACx1dbmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAiXFYMbEhAcBBoPDQoeAQ0I3cqgAAALZJREFUKM+VktsSwyAIRDWKiFf+/2uLSZvEhkxaXnTGs7KsGvN3UYrwC+ffa3D8zCMlxo+QlyfcNmg7v7A/t7VBux/jzkOe54lJURw8ZrHvop0UdM8P+3axGc89aqQ7XuxbjzybMkEUqPLAIPP6/u0g1OYUHnMpTQs02KLxq/0p0Y1O0al+RvqOCcv51CeZF1UeJBjhacoT6PJehTd9k/R7gdgPul7ei3itcWeYPp/sqv4fRhnzAuOaBpbDogV3AAAAAElFTkSuQmCC» /> векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов линейно независима, а после присоединения к ней вектора оказывается линейно зависимой, то вектор можно разложить по векторам , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

Докажем, например, последнее свойство. Так как система векторов — линейно зависима, то существуют числа , не все равные 0, что . В этом равенстве . В самом деле, если , то . Значит, нетривиальная линейная комбинация векторов равна нулевому вектору, что противоречит линейной независимости системы . Следовательно, и тогда , т.е. вектор есть линейная комбинация векторов . Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения и , причем не все коэффициенты разложений соответственно равны между собой (например, ).

Тогда из равенства получаем .

Следовательно, линейная комбинация векторов равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере ), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов . Полученное противоречие подтверждает единственность разложения.

Пример 1.3. Параллелограмм построен на векторах и ; точки и — середины сторон и соответственно (рис. 1.11). Требуется:

а) найти линейные комбинации векторов

б) доказать, что векторы , , линейно зависимы.

а) Так как , то по правилу треугольника: .

Рассуждая аналогично, получаем: . Построим вектор . Из равенства треугольников и следует, что . Тогда .

б) Учитывая, что и , получаем: .

Перенося векторы в левую часть, приходим к равенству , т.е. нетривиальная линейная комбинация векторов , , равна нулевому вектору. Следовательно, векторы , , линейно зависимы, что и требовалось доказать.

Линейно зависимая система уравнений это

Определение 1. Система векторов 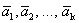называется линейно зависимой, если один из векторов системы можно представить в виде линейной комбинации остальных векторов системы, и линейно независимой — в противном случае.

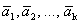
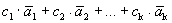
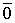
Определение 1´. Система векторов называется линейно зависимой, если найдутся числа с ₁ , с ₂ , …, с _k , не все равные нулю, такие, что линейная комбинация векторов с данными коэффициентами равна нулевому вектору: = , в противном случае система называется линейно независимой.

Покажем, что эти определения эквивалентны.

Пусть выполняется определение 1, т.е. один из векторов системы равен линейной комбинации остальных:

,

.

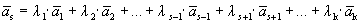
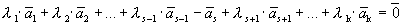
Линейная комбинация системы векторов равна нулевому вектору, причем не все коэффициенты этой комбинации равны нулю, т.е. выполняется определение 1´.

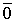
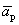
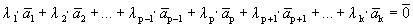
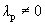
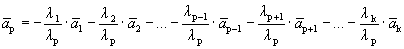
Пусть выполняется определение 1´. Линейная комбинация системы векторов равна , причем не все коэффициенты комбинации равны нулю, например, коэффициенты при векторе .

,

,

.

Один из векторов системы мы представили в виде линейной комбинации остальных, т.е. выполняется определение 1.

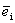
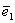
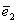
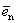
Определение 2. Единичным вектором, или ортом, называется n -мерный вектор , у которого i -я координата равна единице, а остальные — нулевые.

. (1, 0, 0, …, 0),

(0, 1, 0, …, 0),

(0, 0, 0, …, 1).

Теорема 1. Различные единичные векторы n -мерного пространства линейно независимы.

Доказательство. Пусть линейная комбинация этих векторов с произвольными коэффициентами равна нулевому вектору.

= .

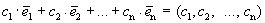
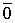
Из этого равенства следует, что все коэффициенты равны нулю. Получили противоречие.

Каждый вектор n -мерного пространства ā(а ₁ , а ₂ , . а _n ) может быть представлен в виде линейной комбинации единичных векторов с коэффициентами, равными координатам вектора

.

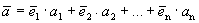
Теорема 2. Если системы векторов содержит нулевой вектор, то она линейно зависима.

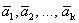
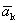
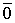
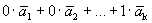
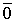
Доказательство. Пусть дана система векторов и один из векторов является нулевым, например = . Тогда с векторами данной системы можно составить линейную комбинацию, равную нулевому вектору, причем не все коэффициенты будут нулевыми:

= .

Следовательно, система линейно зависима.

Теорема 3. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.

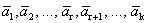
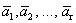
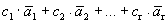
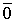
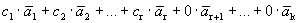
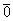
Доказательство. Дана система векторов . Предположим, что система линейно зависима, т.е. найдутся числа с ₁ , с ₂ , …, с _r , не все равные нулю, такие, что = . Тогда

= .

Получилось, что линейная комбинация векторов всей системы равна 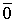, причем не все коэффициенты этой комбинации равны нулю. Следовательно, система векторов линейно зависима.

Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.

Предположим противное, т.е. некоторая подсистема линейно зависима. Из теоремы следует, что вся система линейно зависима. Мы пришли к противоречию.

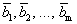
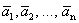
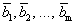
Теорема 4 (теорема Штейница). Если каждый из векторов является линейной комбинацией векторов и m > n , то система векторов линейно зависима.

Следствие. В любой системе n -мерных векторов не может быть больше чем n линейно независимых.

Доказательство. Каждый n -мерный вектор выражается в виде линейной комбинации n единичных векторов. Поэтому, если система содержит m векторов и m > n , то, по теореме, данная система линейно зависима.