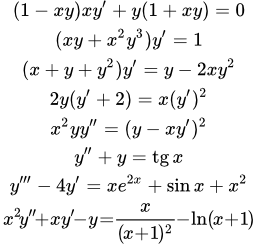Линейное дифференциальное уравнение его решение

Линейные дифференциальные уравнения в высшей математике

Содержание:

Линейные дифференциальные уравнения. Линейные дифференциальные уравнения первого порядка

В предыдущей лекции мы изучали дифференциальные уравнения с разделяющимися переменными. Другим часто встречающимся типом являются линейные дифференциальные уравнения.

Определение 1. Дифференциальное уравнение вида

(1)

называется линейным дифференциальным уравнением первого порядка. Если , то линейное дифференциальное уравнение (ЛДФУ) (1) можно представить в виде:

, (2)

где .

(3)

называется линейным однородным уравнением, соответствующим уравнению (2).

Уравнение (2) — это уравнение с разделяющимися переменными. Действительно

.

Интегрируя это уравнение, получим

где — произвольная первообразная для функции , а положительная постоянная. Из последнего уравнения находим общее решение уравнение (3):

,

где — постоянная произвольного знака.

Одним из наиболее удобных методов решения уравнения (2) является метод подстановки .

Применим этот метод к уравнению (2). Получим

Приравняем выражение в квадратных скобках к нулю и найдем одно из решений этого дифференциального уравнения. Тогда линейное дифференциальное уравнение (2) будет сведено к системе двух дифференциальных уравнений с разделяющимися переменными

Найдя из системы (4) функции и , запишем общее решение уравнения (2) как .

Пример №122

.

Решение:

Данное уравнение — это ЛДФУ первого порядка (2). Применим метод подстановки .

Составим систему (4):

Решим первое уравнение системы:

Так как нам нужно одно ЧР ДФУ, то возьмем = 1. Имеем

Решаем второе уравнение:

Итак, OP Л ДФУ будет таким:

.

Убедимся проверкой в правильности решения:

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Рассмотрим линейное дифференциальное уравнение (ЛДФУ) второго порядка с постоянными коэффициентами

(5)

где — некоторые константы.

Уравнению (5) соответствует однородное ЛДФУ:

. (6)

Пусть — ОР неоднородного уравнения (5), — ЧР неоднородного уравнения (5), — ОР однородного уравнения (6). Имеет место следующее утверждение.

Теорема 1. Общее решение неоднородного уравнения (5) есть сумма общего решения соответствующего ему однородного уравнения (6) и частного решения неоднородного уравнения (5):

(7)

Рассмотрим однородное ЛДФУ (6). Имеет место следующий результат.

Теорема 2. Пусть — решения уравнения (6), тогда их линейная комбинация , где — произвольные константы, также является решением уравнения (6).

Ранее мы отмечали, что ОР ДФУ 2-го порядка зависит от двух произвольных констант. Из теоремы 2 следует, что функция

(8)

является решением уравнения (6). Возникает вопрос: может ли формула (8) определять ОР ДФУ (6). Если да, то при каких условиях? Чтобы разобраться в этом, введем несколько понятий, аналогичных сведениям из линейной алгебры.

Определение 2. Функции называются линейно независимыми, если их линейная комбинация обращается в ноль, т.е.

,

только лишь в случае . В противном случае они называются линейно зависимыми.

Определение 3. Систему функций , состоящую из двух линейно независимых решений уравнения (6), будем называть фундаментальным набором решений этого уравнения.

Имеет место следующий факт.

Теорема 3. Пусть — фундаментальный набор решений уравнения (6), тогда ОР этого уравнения задается формулой:

(9)

Фундаментальный набор решений уравнения (6) находят методом Эйлера в виде функций . Получаем . Подставляя выражения для , и в уравнение (6), имеем

.

Так как , то это соотношение эквивалентно уравнению

. (10)

Определение 4. Алгебраическое уравнение (10) называется характеристическим уравнением однородного ЛДФУ (6).

При решении характеристического уравнения могут возникать три случая.

Случай 1. Дискриминант характеристического уравнения (10) больше нуля. Тогда существует два действительных и различных решения и кратности 1. Соответствующие им решения , образуют фундаментальный набор и ОР уравнения (6) имеет вид

.

Пример №123

.

Решение:

Корнями характеристического уравнения

являются числа = 1 и =-2. Следовательно, ОР однородного ЛДФУ имеет вид

.

Проверкой можно убедиться в правильности решения.

Случай 2. Дискриминант = 0. У характеристического уравнения существует единственный действительный корень кратности 2. Ему соответствует решение . Вторым решением из фундаментального набора будет функция .

Таким образом, ОР имеет вид

.

Пример №124

.

Решение:

имеет единственный действительный корень = -3 кратности 2. Поэтому ОР имеет вид

.

Проверкой можно убедиться в правильности решения.

Случай 3. Дискриминант

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Примеры дифференциальных уравнений с решениями

• Попробуйте решить приведенные ниже дифференциальные уравнения.
• Нажмите на изображение уравнения, и вы попадете на страницу с подробным решением.

Примеры решений дифференциальных уравнений первого порядка

Примеры решений дифференциальных уравнений второго и высших порядков

Найти общее решение дифференциального уравнения, или решение с заданными начальными условиями.

Примеры решений линейных дифференциальных уравнений с постоянными коэффициентами

Примеры решений линейных уравнений в частных производных первого порядка

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .

Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность
, .

Автор: Олег Одинцов . Опубликовано: 28-01-2016 Изменено: 26-11-2021