Линейное уравнение ax b cx d
Линейные уравнения и неравенства с параметром
Уравнение вида
| ax + b = 0, | (1) |
где a,b О R, x — переменная, называется уравнением первой степени (линейным уравнением).
Ниже приведены примеры линейных уравнений:
| a) 2x + 6 = 0, | где a = 2, b = 6; |
| b) x — 2 = 0 | где a = 1, b = -2; |
| c) 0·x + 0 = 0, | где a = b = 0; |
| d) 0·x + 1 /3 = 0, | где a = 0, b = 1 /3; |
| e) — 1 /2x = 0, | где a = — 1 /2; b = 0. |
Уравнение (1) равносильно уравнению ax = —b откуда следует следующее утверждение.
Утверждение 1.
- Если a ≠ 0, то уравнение (1) имеет единственное решение x = — b /a;
- Если a = 0, b ≠ 0, то множество решений уравнения (1) пусто;
- Если a = 0, b = 0, то любое действительное число является решением уравнения (1).
Таким образом, приведенные выше линейные уравнения решаются следующим образом:
a) x = — 6 /2, то есть x = -3;
b) x = 2;
c) любое действительное число является решением данного уравнения;
d) уравнение не имеет решений;
e) x = 0.
Замечание 2. Уравнение (ax + b)(cx + d) = 0 где a, b, c, d О R, сводится к совокупности линейных уравнений
 | ax + b = 0, |
| cx + d = 0. |
Пример 1. Решить уравнения
a) 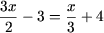 , , | c) —x + 2 = 2 — x, |
| b) 2x + 1 = 2x + 3, | d) (2x + 4)(3x — 1) = 0. |
Решение. a) 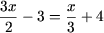
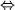
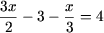
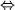
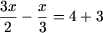
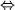
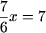
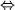
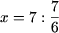
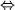
b) 2x + 1 = 2x + 3 Ы 2x — 2x = 3 — 1 Ы 0·x = 2 откуда следует, что уравнение не имеет решений.
c) —x + 2 = 2 — x Ы —x + x = 2 — 2 Ы 0·x = 0, следовательно, любое действительное число является решением уравнения.
| d) (2x + 4)(3x — 1) = 0 Ы |
| Ы |
|
В дальнейшем будут рассматриваться линейные уравнения с параметрами. Под параметром понимается (смотрите тему Уравнения с параметром) фиксированное (но неизвестное) число. Как правило, параметр обозначается первыми буквами латинского алфавита.
Пример 2. Решить уравнения
| a) ax = 1; | e) 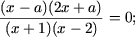 |
| b) a 2 x — 1 = x + a; | f) 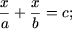 |
| c) ax + b = cx + d; | g)  |
d) 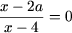 ; ; |
Решение. a) Применяя утверждение 1, получим:
при a ≠ 0 уравнение имеет единственное решение, x = 1 /a;
при a = 0 уравнение примет вид 0·x = 1 и, следовательно, оно не имеет решений.
Ответ: если a О R\<0>, то x = 1 /a; если a = 0, то уравнение не имеет решений.
b) После элементарных преобразований получим: a 2 x — 1 = x + a Ы a 2 x — x = a + 1 Ы x(a 2 — 1) = a + 1.
откуда, применяя утверждение 1, получим:
- если a 2 -1 ≠ 0, то есть a ≠ ± 1, то
или
- если a = 1, то уравнение примет вид 0·x = 2 и, следовательно, не имеет решений;
- если a = -1, то уравнение примет вид 0·x = 0, и, следовательно, любое действительное число является решением этого уравнения.
c) Перепишем уравнение следующим образом (a — c)x = d — b, откуда следует:
- если a — c ≠ 0, то есть a ≠ c, то уравнение имеет единственное решение
- если a = c и d — b ≠ 0, то уравнение примет вид 0·x = d — b ( ≠ 0) и, следовательно, оно не имеет решений;
- если a = c и d = b, то уравнение примет вид 0·x = 0, и, следовательно, множество его решений есть R
d) Область допустимых значений (ОДЗ) уравнения есть x ≠ 4. В ОДЗ уравнение решается следующим образом:
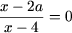 | Ы |
| Ы |
|
Таким образом, если 2a ≠ 4, то есть a ≠ 2, то уравнение имеет единственное решение x = 2a, а если a = 2, то уравнение не имеет решений.
f) Если a = 0 или b = 0, то уравнение не имеет смысла. Пусть a·b ≠ 0. Тогда уравнение равносильно следующему x(b + a) = abc откуда следует:
- если b + a ≠ 0, то есть a ≠ —b, то уравнение имеет единственное решение
- если a = —b и c ≠ 0, то уравнение не имеет решений.
- если a = —b и c = 0, то любое действительное число есть решение данного уравнения.
g) ОДЗ уравнения определяется из системы
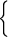 | 5x —a ≠ 0, |
| ax — 1 ≠ 0, |
откуда x ≠ a /5 и, если a ≠ 0, x ≠ 1 /a. Если a = 0, то уравнение примет вид 
откуда 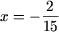

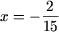
Пусть a ≠ 0. Тогда в ОДЗ уравнение примет вид 2(ax — 1) = 3(5x — a), откуда (2a — 15)x = 2 — 3a и, следовательно,
- если 2a — 15 ≠ 0, то есть
то получим
;
- если 2a-15 = 0, то есть
то уравнение не имеет решений.
Таким образом для 

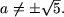
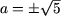
В случае второго ограничения получим 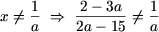
Таким образом, если 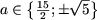
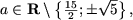
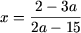
Пример 3. Решить уравнения
| a) |x — a| = 2; | c) |x — a| + |x — 2a| = a; |
| b) |x| + |x — a| = 0; | d) |x — 1| + |x — 2| = a. |
Решение. a) Используя свойство модуля, получим:
| |x — a| = 2 Ы |
| Ы |
|
Таким образом, для любого действительного a уравнение имеет два различных решения, x1 = a + 2 и x2 = a — 2.
b) Левая часть уравнения принимает неотрицательные значения (как сумма двух неотрицательных слагаемых), а правая часть равна нулю. Следовательно,
| или |
|
Таким образом, если a = 0, то система (а, следовательно, и уравнение) имеет единственное решение x = 0, а если a ≠ 0, то система (и исходное уравнение) решений не имеет.
c) Так как | f(x)| = |-f(x)| уравнение можно переписать следующим образом |x — a| + |2a — x| = a.
Очевидно, что если a 0. Тогда a = |a| = |(2a — x) + (x — a)|, и уравнение примет вид |x — a| + |2a — x| = |(2a — x) + (x — a)|. Это уравнение равносильно (см. свойства модуля) неравенству (2a — x)(x — a) ≥ 0 откуда, учитывая, что 0 О [a;2a].
если a 0, то уравнение имеет бесконечное число решений — любое число a ≤ x ≤ 2a.
d) Очевидно, что уравнение имеет решения только при a > 0. Рассмотрим три случая:
- Пусть x —x + 1 — x + 2 = a или -2x = a — 3 откуда
. Поскольку x
откуда a > 1. Таким образом, если a > 1, то
;
- Пусть x О [1;2]. Тогда |x — 1| = x — 1, |x — 2| = -(x-2) и уравнение примет вид x — 1 — x + 2 = a, 0·x = a — 1. Используя утверждение 1, получим:
если a = 1, то любое действительное число из отрезка [1;2] есть решение исходного уравнения;
если a ≠ 1, то решений нет.
Пусть x > 2. Тогда |x — 1| = x — 1, |x — 2| = x — 2 и уравнение примет вид x — 1 + x — 2 = a откуда 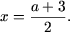
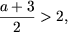
если a > 1, то уравнение имеет два различных решения 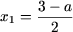
если a = 1, то любое число отрезка [1;2] есть решение уравнения;
если a Линейные неравенства
| ax + b > 0, ax + b ≥ 0, ax + b О R, x — переменная, называются неравенствами первой степени (линейными неравенствами). Поскольку все неравенства (2) решаются аналогично, приведем решение лишь первого из них: ax + b > 0. Рассмотрим следующие случаи:
Рассмотрим несколько примеров. Пример 1. Решить неравенства
|
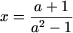 или
или 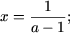
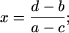
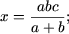
 то получим
то получим  то уравнение не имеет решений.
то уравнение не имеет решений.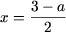 . Поскольку x
. Поскольку x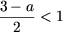 откуда a > 1. Таким образом, если a > 1, то
откуда a > 1. Таким образом, если a > 1, то 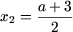

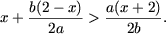
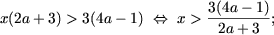
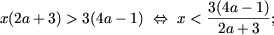
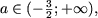 то
то 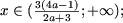
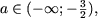 то
то 
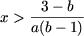
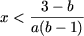

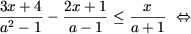
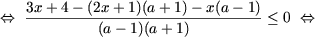
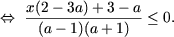
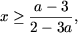
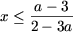 .
.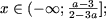
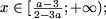
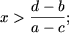
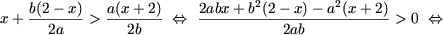
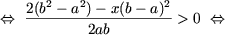
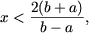
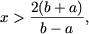
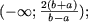 если a и b — противоположных знаков (ab
если a и b — противоположных знаков (ab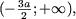 (а, следовательно, и множеством решений неравенства) явяется множество
(а, следовательно, и множеством решений неравенства) явяется множество 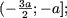
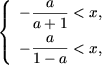 откуда (учитывая, что x > 0) получим
откуда (учитывая, что x > 0) получим 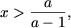 а вторая система совокупности примет вид
а вторая система совокупности примет вид 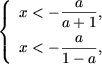 и, так как a > 1 влечет
и, так как a > 1 влечет 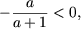 а x > 0, система не имеет решений.
а x > 0, система не имеет решений.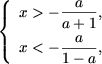 или
или 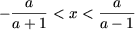 откуда, заметив, что
откуда, заметив, что 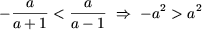 получим, что первая система совокупности несовместна. Из второй системы получим
получим, что первая система совокупности несовместна. Из второй системы получим 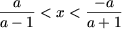 и, учитывая, что x > 0, получим
и, учитывая, что x > 0, получим 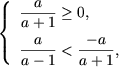 откуда a О [0;1), то неравенство не имеет решений, а если a О (-1;0), то множество решений неравенства есть
откуда a О [0;1), то неравенство не имеет решений, а если a О (-1;0), то множество решений неравенства есть 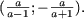
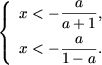 Так как a 0, то в этом случае исходное неравенство не имеет решений. Вторая система совокупности примет вид
Так как a 0, то в этом случае исходное неравенство не имеет решений. Вторая система совокупности примет вид 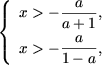 и, поскольку x > 0, получим
и, поскольку x > 0, получим 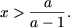
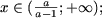


 .
.
 :
:


 :
:







 .
. решаем квадратное уравнение a(t 2 – 2) + bt + c = 0
решаем квадратное уравнение a(t 2 – 2) + bt + c = 0 , после замены
, после замены  получаем уравнение t 2 – 2t – 3 = 0
получаем уравнение t 2 – 2t – 3 = 0 – уравнение не имеет корней.
– уравнение не имеет корней.
 имеем (t + 14)(t + 11 ) = 4.
имеем (t + 14)(t + 11 ) = 4.


