Линейные дифференциальные уравнения произвольного порядка
4.1 Линейное однородное дифференциальное уравнение
§ Линейное однородное дифференциальное уравнение имеет вид
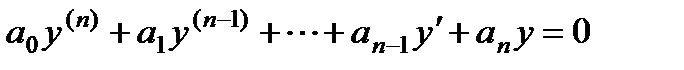
где коэффициенты аk являются непрерывными функциями от х (в частности они могут быть постоянными или нулями). Полагая коэффициент а0(х) не равным нулю в некотором интервале 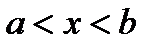
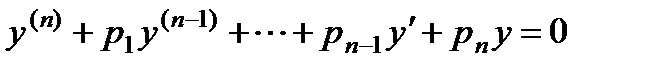
В дальнейшем говоря о линейном однородном уравнении мы будем подразумевать, что оно приведено к виду (1) с коэффициентом при старшей производной равным единице.
§ Для уравнения (1) справедливы следующие теоремы:
Т е о р е м а 1. Если у1 и у2 суть два (частных) решения уравнения (1), то у1 + у2
есть также решение этого уравнения.
Т е о р е м а 2. Если у1 есть решение уравнения (1), то С у1 есть также решение этого уравнения (С – любая постоянная).
Следствие. Если у1, у2,…,уп суть частные решения линейного однородного уравнения п – гопорядка, то выражение 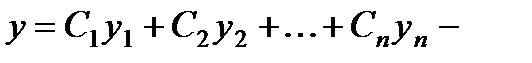
§ Вопрос о том, каким условиям должны удовлетворять частные решения, чтобы это
выражение являлось общим решением однородного уравнения, разрешается в связи с понятием линейной зависимости функций. Функции 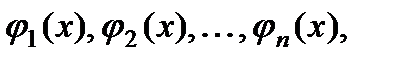
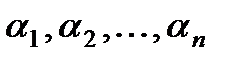
Если не существует таких постоянных 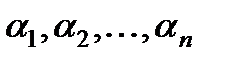

§ Пусть мы имеем п функций от х, имеющих непрерывные производные до

называется определителем Вронского этих функций.
Т е о р е м а 3. Если функции у1 , у2 , … , уп линейно зависимы, то определитель
Вронского тождественно равен нулю.
Т е о р е м а 4. Если решения у1 , у2 , … , уп линейно независимы [в интервале
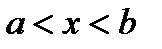
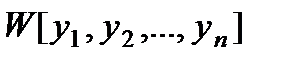
Теоремы 3 и 4 можно объединить в следующей формулировке: определитель
Вронского, составленный для системы п решений линейного уравнения п-го порядка (1), или тождественно равен нулю, или не обращается в нуль ни в одной точке того интервала, где коэффициенты уравнения непрерывны.
Любая система из п линейно независимых частных решений линейного однород-
ного уравнения (1) называется фундаментальной системой.
Т е о р е м а 5. Для всякого линейного однородного дифференциального уравнения
существует фундаментальная система.
Т е о р е м а 6. Если у1 , у2 , … , уп образуют фундаментальную систему решений
уравнения 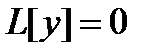
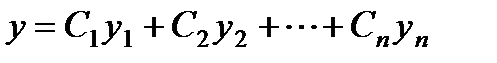
П р и м е р 13. Уравнение 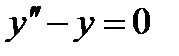
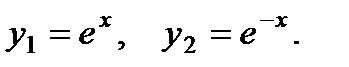

Следовательно, 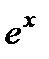
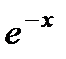
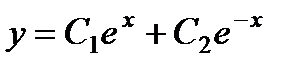
Т е о р е м а 7. Если мы имеем п + 1 частных решений уравнения (1)
то между ними необходимо существует линейная зависимость.
Т е о р е м а 8. Фундаментальная система вполне определяет линейное
однородное уравнение со старшим коэффициентом, равным единице.
Решим теперь такую задачу:
Дана фундаментальная система (в интервале 
соответствующее дифференциальное уравнение.
Для этой цели приравниваем нулю следующий определитель, в котором у обозна-
чает искомую функцию:

Разлагая его по элементам последнего столбца, мы убеждаемся в том, что равенство (2) представляет собой однородное дифференциальное уравнение п-го порядка относительно функции у. При подстановке вместо у функций уi (i = 1, 2, …, п) мы получаем определитель с двумя равными столбцами. Он тождественно равен нулю; следовательно, уравнение (2) допускает частные решения у1 , у2 , … , уп .
П р и м е р 14. Построить уравнение, имеющее в качестве фундаментальной системы функции х, х 2 , х 3 . Строим уравнение по формуле (2):
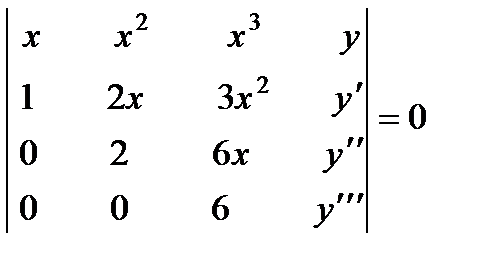
Раскрывая определитель по элементам последнего столбца, получаем:
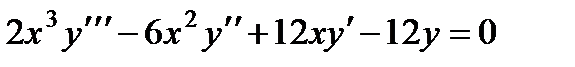
Здесь 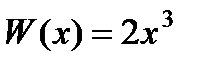
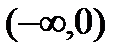

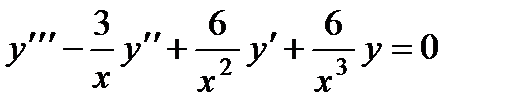
§ Понижение порядка линейного однородного уравнения
1. Для линейного однородного уравнения (1) справедлива формула Остроградского –
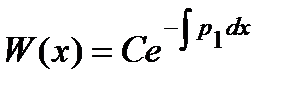
Применим ее к нахождению общего решения уравнения второго порядка:
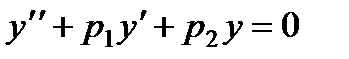
у которого нам известно одно частное решение у1.
Пусть у есть любое решение этого уравнения, отличное от у1. Составляем
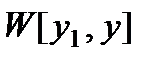
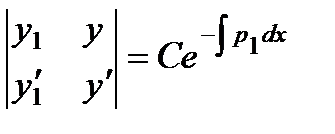
Раскрывая определитель, имеем линейное уравнение первого порядка:

делим обе части на 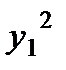
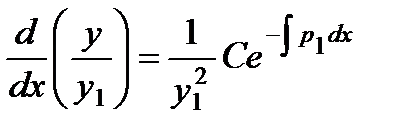
откуда у определяется квадратурой:
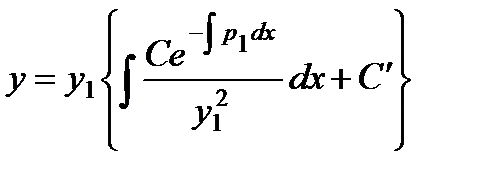
Полученное решение содержит два произвольных постоянных и, следовательно, является общим.
Итак, если известно одно частное решение линейного однородного уравнения
второго порядка, общее решение находится квадратурами.
Примечание. При решении задач пользоваться готовой квадратурой не рекоменду-
ется. Следует повторить ход решения.
П р и м е р 15. Проинтегрировать уравнение
Легко убедиться, что частным решением этого уравнения является у1 = х. В нашем случае 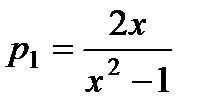
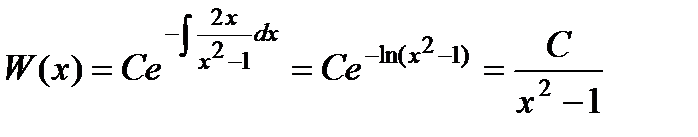
Теперь раскрываем выражение 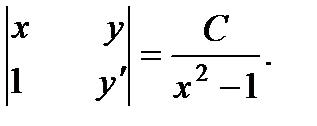
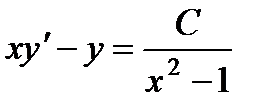
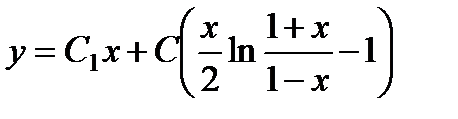
2. Понижение порядка в уравнении (1) при известном частном решении у1(х) можно
произвести с помощью подстановки у = у1z , где z – новая неизвестная функция.
В результате этой подстановки для z получим опять уравнение порядка п ,
которое не будет содержать неизвестной функции z , и, как следует из раздела 3.1, подстановка 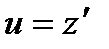
П р и м е р 16. Найти общее решение уравнения 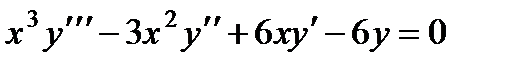
Легко находим частное решение у1 = х. Подстановка у = хz приводит к уравнению третьего порядка для z : 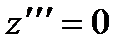
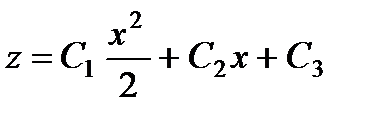
Так как у = хz , то окончательно 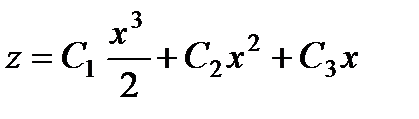
4.2 Линейное неоднородное дифференциальное уравнение
Рассмотрим неоднородное линейное дифференциальное уравнение вида:

Однородное линейное уравнение с теми же коэффициентами, но с правой частью,
равной нулю, называется однородным уравнением, соответствующим неоднородному уравнению (3).
Т е о р е м а 1. Если известно какое-нибудь частное решение Y неоднородного уравнения (3), то общее его решение есть сумма этого частного решения и общего решения соответствующего однородного уравнения, т.е. 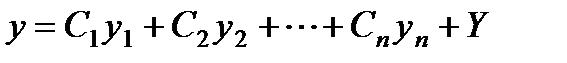
Здесь 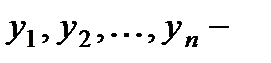
П р и м е р 17. Найти общее решение уравнения 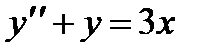
Легко видеть, что его частным решением будет у = 3х. Соответствующее однородное уравнение 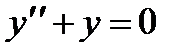
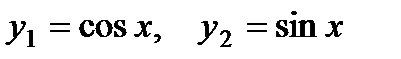
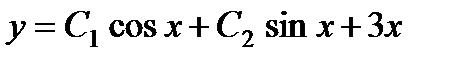
Т е о р е м а 2. Если известна фундаментальная система решений соответствую-
щего однородного уравнения, то общее решение неоднородного уравнения может быть найдено при помощи квадратур (методом вариации произвольных постоянных).
Решение неоднородного уравнения (3) ищется в виде:
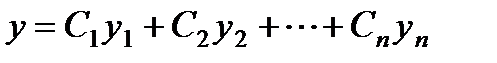
где 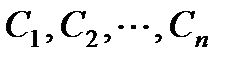
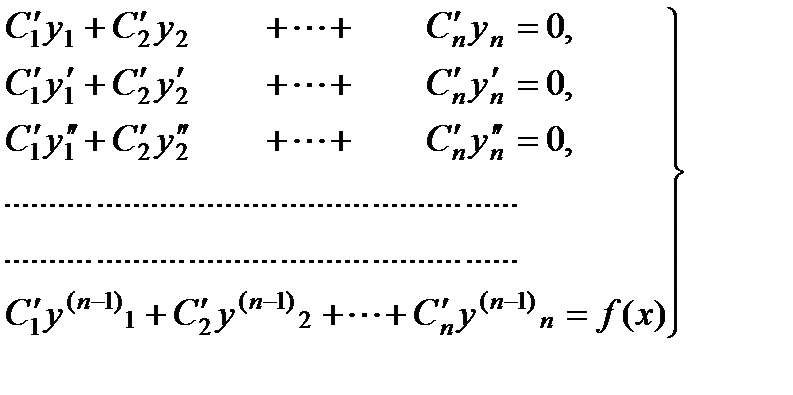
П р и м е р 18. Решить уравнение 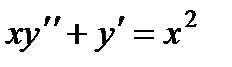
Решая однородное уравнение 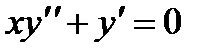
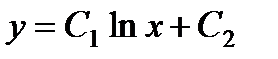
Следовательно, фундаментальная система решений имеет вид
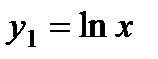
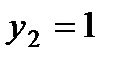
Составляем систему (4), учитывая, что канонический вид уравнения есть 
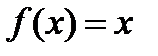

и, следовательно, по формуле 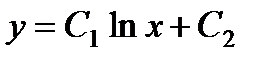
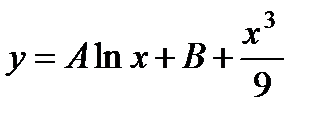
Последнее слагаемое в правой части есть не что иное, как частное решение исходного неоднородного уравнения.
4.3 Линейные уравнения с постоянными коэффициентами
4.3.1 Линейные однородные уравнения
Линейное однородное дифференциальное уравнение с постоянными
коэффициентами п-го порядка имеет вид
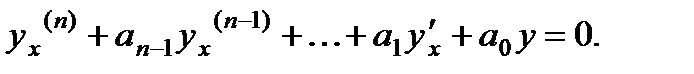
Общее решение этого уравнения определяется корнями характеристического уравнения
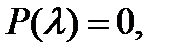
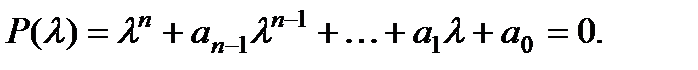
Возможны следующие случаи:
§ Все корни 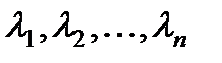

§ Имеется т равных действительных корней: 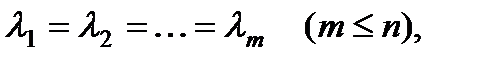
§ Имеется т равных комплексно сопряженных корней: 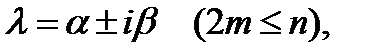
где 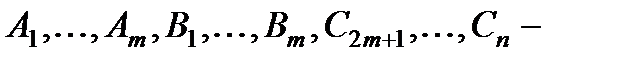
§ В общем случае, когда имеются r различных корней 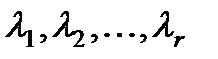
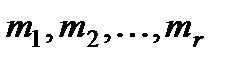
где 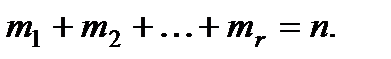
где 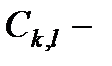
Если имеются комплексно сопряженные корни уравнения 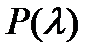
П р и м е р 19. Решить уравнение 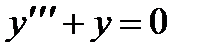
Его характеристическое уравнение 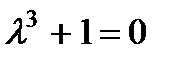
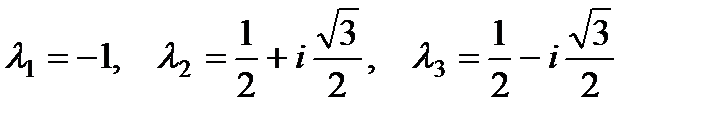

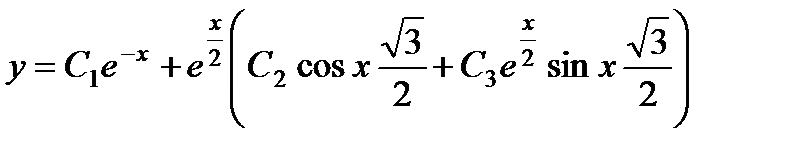
П р и м е р 20. Решить уравнение 
Его характеристическое уравнение 
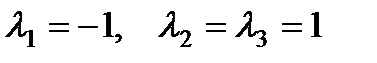
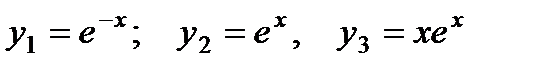

П р и м е р 21. Решить уравнение 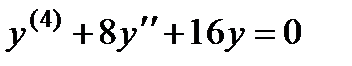
Его характеристическое уравнение 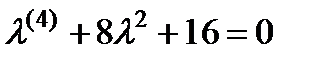
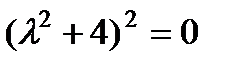
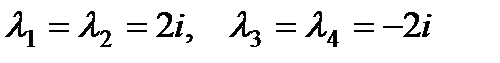
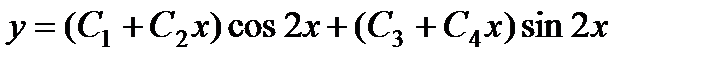
4.3.2 Линейные неоднородные уравнения
Когда найдено решение соответствующего однородного уравнения, т.е. известна
его фундаментальная система решений, то решение неоднородного уравнения согласно теореме 2 (разд. 4.2) находится в квадратурах.
Если правая часть неоднородного уравнения принадлежит к одному из указанных в
нижеследующей таблице типов, то решение неоднородного уравнения с постоянными коэффициентами может быть найдено вообще без интегрирования методом неопределенных коэффициентов.
В предлагаемой таблице перечислены типы правых частей уравнений и соответст-
вующие типы частных решений.
Вид частных решений неоднородного уравнения с постоянными коэффициентами 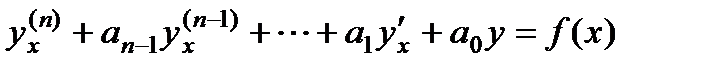
Вид правой части 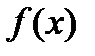 | Корни характеристического уравнения 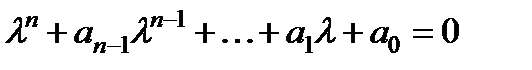 | Вид частного решения 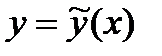 |
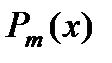 | Число 0 не является корнем характеристического уравнения | 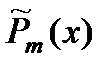 |
| Число 0 является корнем характеристического уравнения (кратности r) | 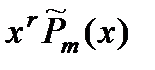 | |
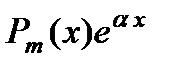 ( ( 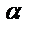 — действительное число) — действительное число) | Число 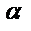 не является корнем характеристического уравнения не является корнем характеристического уравнения | 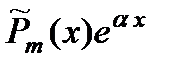 |
Число 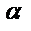 является корнем характеристического уравнения (кратности r) является корнем характеристического уравнения (кратности r) |  | |
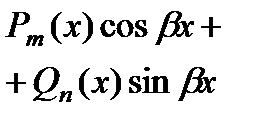 | Число 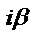 не является корнем характеристического уравнения не является корнем характеристического уравнения | 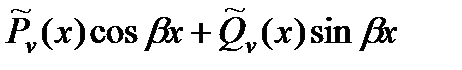 |
Число  является корнем характеристического уравнения (кратности r) является корнем характеристического уравнения (кратности r) | 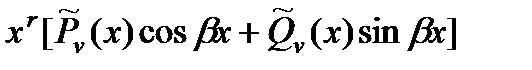 | |
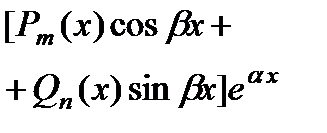  | Число 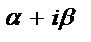 не является корнем характеристического уравнения не является корнем характеристического уравнения | 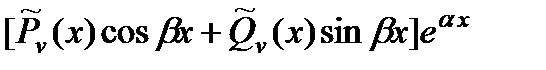 |
Число 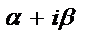 является корнем характеристического уравнения (кратности r) является корнем характеристического уравнения (кратности r) |  | |
Обозначения: 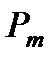 и и 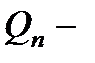 многочлены степени т и п с заданными коэффициентами; многочлены степени т и п с заданными коэффициентами;  и и 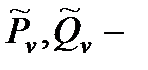 многочлены степени т и v, коэффициенты которых определяются в результате подстановки данного частного решения в исходное уравнение; v = max (m, n). многочлены степени т и v, коэффициенты которых определяются в результате подстановки данного частного решения в исходное уравнение; v = max (m, n). |
П р и м е р 22. Найти частное решение неоднородного уравнения 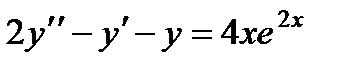
Характеристическое уравнение 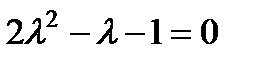
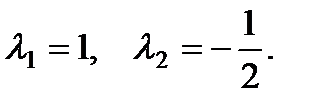
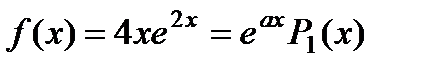
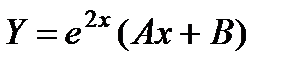
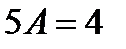
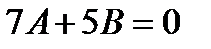
Таким образом, искомое частное решение 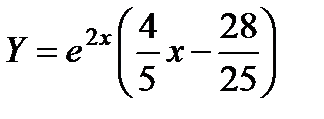
П р и м е р 23. Найти частное решение неоднородного уравнения 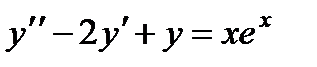
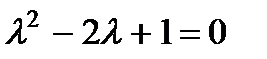
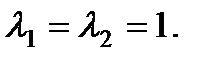
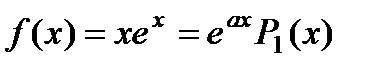
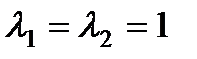
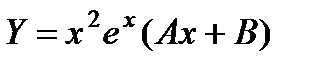
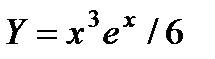
П р и м е р 24. Найти частное решение неоднородного уравнения 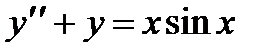
Характеристическое уравнение 
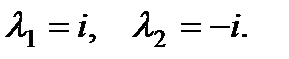
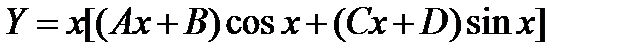

Отсюда находим 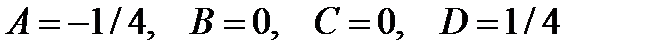
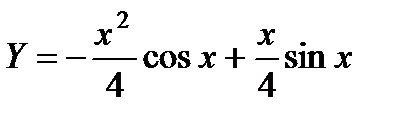
П р и м е р 25. Теперь рассмотрим пример с комбинированной правой частью:
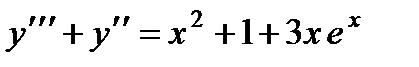
Обозначим 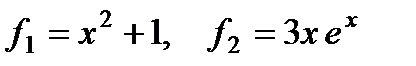
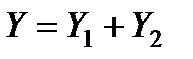
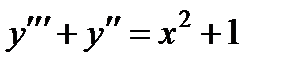

Характеристическое уравнение 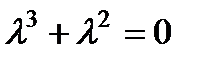
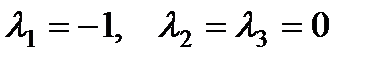
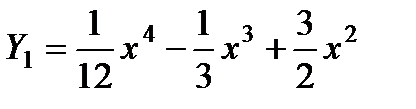
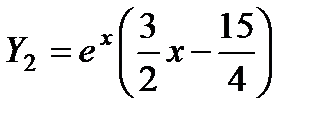

Если правая часть линейного уравнения с постоянными коэффициентами не имеет вида, приведенного в таблице и не является их линейной комбинацией, то для нахождения частного решения следует применить метод вариации произвольных постоянных.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Предлагается 25 вариантов индивидуальных заданий, включающих в себя
различные дифференциальные уравнения и две задачи на составление дифференциальных уравнений. Каждый вариант состоит из 8 заданий. Если в задании не указаны начальные условия, то следует найти общее решение заданного уравнения, а если к уравнению добавлены начальные условия, то следует решить задачу Коши. В седьмом и восьмом задании следует составить дифференциальное уравнение (исходя из условий задачи) и решить его.
Вариант 1
1.
2.
3.
4.
5.
6.
7. Два одинаковых груза подвешены к кольцу пружины. Найти закон движения одного из грузов, если другой оборвется. Дано, что удлинение пружины под влиянием одного из грузов равно а см.
8. Найти кривые, у которых в любой точке радиус кривизны вдвое больше отрезка нормали, заключенного между этой точкой кривой и осью абсцисс, если известно, что кривая обращена выпуклостью к оси ординат.
Вариант 2
1.
2.
3.
4.
5.
6.
7. Последовательно включены источники тока, напряжение каждого меняется по закону 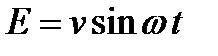
8. Найти плоские кривые, радиус кривизны которых пропорционален кубу длины отрезка нормали.
Вариант 3
1.
2.
3.
4.
5.
6.
7. Найти кривые, у которых радиус кривизны равен нормали.
8. Материальная точка массы т движется прямолинейно к неподвижному центру, притягивающему ее силой, обратно пропорциональной кубу расстояния от точки до неподвижного центра. В начальный момент точка находится в покое и стоит от центра на расстоянии х0 . Определить время, по истечении которого точка достигает центра.
Вариант 4
1.
2.
3.
4.
5.
6.
7. Найти линию, длина дуги которой, отсчитываемая от некоторой точки, пропорциональна угловому коэффициенту касательной в конечной точке дуги.
8. Материальная точка массы т движется прямолинейно под действием силы притяжения к неподвижному центру, пропорциональной расстоянию от точки до центра (k1 > 0). Сила сопротивления среды пропорциональна скорости (k2 > 0). В начальный момент времени точка находится на расстоянии а от центра, скорость равна v0 и направлена по прямой, соединяющей точку с центром. Найти закон движения, если (k2 2 0).
Вариант 8
1. 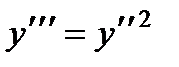
2.
3.
4.
5.
6.
7. Найти кривые постоянного радиуса кривизны.
8. Найти закон прямолинейного движения материальной точка массы т под действием отталкивающей силы, обратно пропорциональной кубу расстояния от точки до неподвижного центра. В начальный момент точка находится в покое и отстоит от центра на расстоянии х0 .
Вариант 9
1.
2.
3.
4.
5.
6.
7. Найти линию, для которой проекция радиуса кривизны на ось Оу есть величина постоянная, равная 7.
8. Моторная лодка весом 300 кг движется прямолинейно с начальной скоростью
66 м/с . Сопротивление воды пропорционально скорости и равно 10 кг при скорости 1 м/с. Через какое время скорость лодки будет 8 м/с ?
Вариант 10
1.
2.
3.
4.
5.
6. 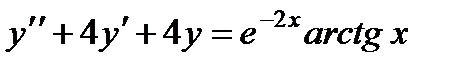
7. При каких k и 
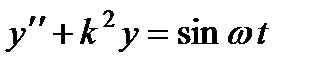
8. Материальная точка массы т движется прямолинейно под действием силы отталкивания от неподвижного центра, пропорциональной расстоянию от точки до центра (k1 > 0). Сила сопротивления среды пропорциональна скорости (k2 > 0). В начальный момент точка находится на расстоянии а от центра, скорость равна v0 и направлена по прямой, соединяющей точку с центром. Найти закон движения точки.
Вариант 11
1.
2.
3.
4.
5.
6.
7. Составить дифференциальное уравнение семейства плоских кривых 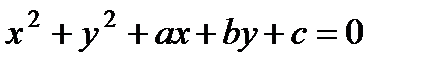
8. Цепь длиной 6м соскальзывает со стола. В момент начала движения со стола свисал 1м цепи. В течении какого времени со стола соскользнет вся цепь (трением пренебрегаем).
Вариант 12
1.
2.
3.
4.
5.
6.
7. Найти интегральную кривую уравнения 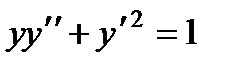
8. Частица массы т движется по оси Ох, отталкиваясь от точки х = 0 с силой 3mr0 и притягиваясь к точке х = 1 с силой 4mr1 , где r0 и r1 – расстояние до этих точек. Определить движения частицы с начальными условиями х(0) = 2, v(0) = 0.
Вариант 13
1.
2.
3.
4.
5.
6.
7. Найти уравнение кривых, у которых радиус кривизны в любой точке равен длине отрезка нормали заключенного между этой точкой и осью абсцисс, если кривая вогнута вниз.
8. Тело массы т движется прямолинейно под действием постоянной силы р. Найти скорость движения и пройденный им путь как функцию времени, если в начальный момент они оба равны нулю, а сопротивление среды пропорционально квадрату скорости.
Вариант 14
1.
2.
3.
4.
5.
6.
7. Найти кривые, у которых проекции радиуса кривизны на ось постоянны.
8. Тяжелое тело без начальной скорости скользит по наклонной плоскости. Найти закон движения, если угол наклона равен 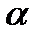
Указание: сила трения равна 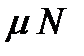
Вариант 15
1.
2.
3.
4.
5.
6.
7. При каких а и b изо всех решений уравнения 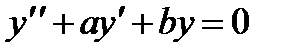
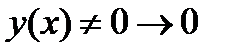

8. Груз массой 4кг подвешен на пружине и увеличивает ее длину на 1см . Найти закон движения груза, если верхний конец пружины совершает гармоническое вертикальное колебание 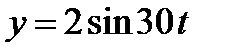
Вариант 16
1.
2.
3.
4.
5.
6.
7. Найти форму равновесия однородной нерастяжимой нити под действием силы тяжести (цепная линия).
8. Найти закон движения тела, падающего без начальной скорости. Допуская, что сопротивление воздуха пропорционально квадрату скорости и что скорость имеет своим пределом при 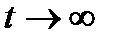
Вариант 17
1.
2.
3.
4.
5.
6.
7. Определить формулу равновесия нерастяжимой нити с закрепленными концами, на которую действует нагрузка так, что на каждую единицу длины горизонтальной проекции нагрузка одинакова (цепи цепного листа). Весом самой нити пренебречь.
8. Материальная точка медленно погружается в жидкость. Найти закон движения, считая, что при медленном погружении сопротивление жидкости пропорционально скорости погружения.
Вариант 18
1.
2.
3.
4.
5.
6.
7. Найти уравнения кривых, у которых радиус кривизны в любой точке равен длине отрезка нормали, заключенного между этой точкой и осью абсцисс, если кривая вогнута вверх.
8. Мяч массой 400г падает с высоты 16,7м без начальной скорости. Сопротивление воздуха пропорционально скорости мяча и равно 0,0048Н при скорости 1м/с. Вычислить время падения и скорость мяча в конце падения. Принять g = 10м/с 2 .
Вариант 19
1.
2.
3.
4.
5.
6.
7. Найти кривую, у которой радиус кривизны вдвое больше нормали.
8. Балка длины l , встроенная правым концом в стену, изгибается силой р , приложенной к левому концу и равномерно распределенной нагрузкой q. Найти уравнение изогнутой балки и ее максимальный прогиб.
Вариант 20
1.
2.
3.
4.
5.
6.
7. При каких а и b все решения уравнения 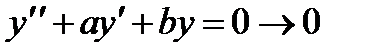
8. Если тело медленно погружается в воду, то его скорость v и ускорение w приближенно связаны уравнением 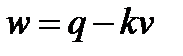
Вариант 21
1.
2.
3.
4.
5.
6.
7. Найти плоские кривые, у которых радиус кривизны пропорционален длине отрезка нормали. Рассмотреть случаи, когда коэффициент пропорциональности k равен +1 , +2.
8. Найти скорость, с которой тело падает на поверхность Земли, если считать, что оно падает с бесконечно большой высоты и движение происходит только под влиянием притяжения Земли. Радиус Земли считать равным 6400км.
Вариант 22
1.
2.
3.
4.
5.
6.
7. Найти кривые, у которых радиус кривизны обратно пропорционален косинусу угла между касательной и осью абсцисс.
8. Материальная точка массы т отталкивается от центра О с силой, пропор-циональной расстоянию. Сопротивление среды пропорционально скорости движения. Найти закон движения.
Вариант 23
1.
2.
3.
4.
5.
6.
7. Найти уравнение кривой, касающейся оси абсцисс в начале координат, если ее кривизна в любой точке равна 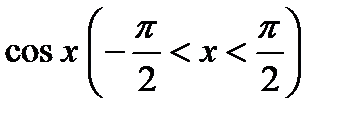
8. Найти закон движения тела, падающего в воздухе без начальной скорости, считая сопротивление воздуха пропорциональным квадрату скорости.
Вариант 24
1.
2.
3.
4.
5.
6.
7. Найти кривую, у которой радиус кривизны пропорционален кубу нормали.
8. Балка длины l, лежащая концами на двух опорах, находится под действием равномерно распределенной нагрузки интенсивности q. Найти уравнение прогнутой оси балки и ее максимальный прогиб, выбрав начало координат в середине нагруженной балки.
Вариант 25
1.
2.
3.
4.
5.
6.
7. Найти кривые, у которых радиус кривизны пропорционален модулю радиус-вектора из начала координат до точки кривой.
8. Груз массы т покоится на упругой рессоре. На груз действуют восстанав-ливающая сила пропорциональная отклонению 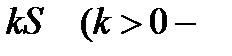
Список литературы
1. Егоров А.И. Обыкновенные дифференциальные уравнения с приложениями. – Физматлит, 2005.
2. Федорюк М.В. Обыкновенные дифференциальные уравнения. Издание 3 – URSS: 2009.
3. Задачи и упражнения по математическому анализу для ВТУЗов под редакцией Б.П. Демидовича. – М: «Интеграл – пресс», 1997.
4. Бабиков Ю.Н. Курс обыкновенных дифференциальных уравнений. – М: «Высшая школа», 1991.
5. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – Ижевск: «РХД», 2000.
6. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. – М:Наука, 1980.
7. Арнольд В.И. Обыкновенные дифференциальные уравнения. – «Регулярная и хаотическая динамика», 2000.
Обыкновенные дифференциальные уравнения
Содержание:
Обыкновенные дифференциальные уравнения
При решении многих задач математики, техники, экономики и других отраслей науки бывает трудно установить закон, связывающий искомые и известные переменные величины. Но удается установить связь между производными или дифференциалами этих переменных, которая выражается уравнениями или системами уравнений. Такие уравнения называют дифференциальными уравнениями. Термин «дифференциальное уравнение» введен в 1676 году В. Лейбницом.
Мы рассмотрим только уравнения с функциями одной переменной и обычными производными, которые называют обычными дифференциальными уравнениями.
Основные понятия о дифференциальных уравнениях
Определение. Дифференциальным уравнением называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и еепроизводные или дифференциалы разных порядков, то есть уравнение

Важно понять, что искомая функция в дифференциальном уравнении входит под знак дифференциала или под знак производной.
Определение. Порядком дифференциального уравнения называется наивысший порядок производной от неизвестной функции, входящей в дифференциальное уравнение.
Так, уравнение y’ – 2 xy 2 + 5 = 0 является дифференциальным уравнением первого порядка, а уравнения y» + 2 y’ – y – sin x = 0 — дифференциальным уравнением второго порядка.
Определение. Решением дифференциального уравнения (7.1) называется такая функция y = φ (x), которая при подстановке в уравнение (7.1) превращает его в тождество.
Например, для дифференциального уравнения
y’- 2 x = 0 (7.2)
решением является функция y = x 2 . Найдем производную y’= 2x и подставим в уравнение, получим: 2x – 2x = 0, 0 ≡ 0.
Следует заметить, что y = x 2 не единственное решение уравнения. Это уравнение имеет бесконечное множество решений, которые можно записать так: y = x 2 + C.
Дифференциальные уравнения первого порядка
Определение. Дифференциальным уравнением первого порядка называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и ее первую производную:
F (x, y, y’) = 0. (7.3)
Поскольку производную можно записать в виде отношения дифференциалов, то в уравнение производная может не входить, а будут входить дифференциалы неизвестной функции и независимой переменной.
Если уравнение (7.2) решить относительно у’, то оно будет иметь вид:
y’= f (x, y) или 
Простые примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений. Это мы видим на примере уравнения (7.2). Легко убедиться также, что дифференциальное уравнение 


Как видим, в решение указанных дифференциальных уравнений входит произвольное число C. Предоставляя постоянной C различные значения, будем получать различные решения дифференциального уравнения.
Определение. Общим решением дифференциального уравнения (7.3) называется функция
у = φ (х, С), (7.5)
которая зависит от одной произвольной постоянной и удовлетворяет дифференциальное уравнение при произвольном значении C.
Если функция (7.5) выражается неявно, то есть в виде
Ф (х, у, С) = 0, (7.6)
то (7.6) называется общим интегралом дифференциального уравнения.
Определение. Частным решением дифференциального уравнения (7.3) называется такое решение, которое получается из общего решения (7.5) при некотором конкретном значении постоянной C.
Ф (х, у, С0) называется частным интегралом дифференциального уравнения.
На практике при решении конкретных задач часто приходится находить не все решения, а решение, которое удовлетворяет определенным начальным условиям. Одной из таких задач является задача Коши, которая для дифференциального уравнения первого порядка формулируется так: среди всех решений дифференциального уравнения (7.3) найти такое решение y, которое при заданном значении независимой переменной x = x0 равна заданному значению y0 , то есть y (x0) = y0 или 
Условие (7.7) называется начальным условием решения.
Покажем на примере, как найти частное решение дифференциального уравнения, когда известно общее решение и задано начальное условие.
Мы видим, что дифференциальное уравнение 

Ответ на вопрос о том, при каких условиях уравнение (7.4) имеет
решение, дает теорема Коши.
ТЕОРЕМА (о существовании и единственности решения). Если функция f (x, y) и ее частная производная 
Теорема Коши дает достаточные условия существования единого решения дифференциального уравнения (7.4). Заметим, что в условии теоремы не требуется существования частной производной 
График произвольного частного решения дифференциального уравнения называется интегральной кривой. Общему решению отвечает семья кривых. Так мы проверили, что уравнение 
которые проходят через начало координат (рис. 1).
Уравнение 
Если задано начальное условие 
интегральных кривых мы выбираем проходящую через точку M0 (x0; y0).
Надо заметить, что нахождение решения дифференциального уравнения часто называют интегрированием уравнения. При этом операцию интегрирования функций называют квадратурой.
Общего метода решения дифференциальных уравнений первого порядка не существует. Рассмотрим некоторые методы решения отдельных типов дифференциальных уравнений.
Дифференциальные уравнения с разделенными переменными
Определение. Уравнение вида
f1 (y) dy = f2 (x) dx, (7.8)
где f1 (y) и f2 (x) — заданные функции, называется дифференциальным уравнением с разделенными переменными.
В этом уравнении каждая из переменных находится только в той части уравнения, где находится ее дифференциал. Уравнение dy = f (x) dx является частным случаем уравнения (7.8). Чтобы решить уравнение (7.8), надо проинтегрировать обе его части: 
Понятно, что произвольную постоянную С можно записывать в любой части равенства.
Пример 1. Решить дифференциальное уравнение: 
Решение. Проинтегрируем левую и правую части уравнения, причем для удобства потенцирования, произвольную постоянную запишем в виде ln |C| получим: 


Подставляя в общее решение начальное условие, найдем С: 2 = С.
Итак,

Дифференциальные уравнения с разделяющимися переменными
Определение. Уравнение вида
f1 (x) f2 (y) + g1 (x) g2 (y) = 0 (7.9)
называется дифференциальным уравнением с разделяющимися переменными.
В этом уравнении переменные еще не разделены, но, поделив обе части уравнения на произведение f2 (y) g1 (x), получим уравнение с разделенными переменными:
Интегрируя это уравнение, запишем 
Получили общий интеграл данного уравнения.
Пример 2. Решить дифференциальное уравнение
x (y + 1) dx – (x 2 + 1) ydy = 0.
Решение. Поделим обе части этого уравнения на (y + 1) (x 2 + 1), после чего получим 
Интегрируя, получим



Пример 3. Найти частное решение дифференциального уравнения (1 + x 2 ) dy + ydx = 0, удовлетворяющее начальному условию y (0) = 1.
Решение. Отделим переменные, поделив уравнение на y ⋅ (1 + x 2 ), и проинтегрируем данное уравнение:
Получили общий интеграл дифференциального уравнения.
Используя начальное условие, найдем произвольную постоянную С:
ln 1 + arctg 0 = C, откуда C = 0.
Найденную постоянную подставим в общий интеграл и отыщем частное решение:

Однородные дифференциальные уравнения
Определение. Функция двух переменных f (x, y) называется однородной n- го измерения, если выполняется условие
Например, f (x, y) = x 2 + y 2 , f (tx, ty) = t 2 f (x 2 + y 2 ) — однородная функция второго измерения.
Определение. Дифференциальное уравнение
y ‘= f (x, y) (7.10)
называется однородным, если функция f (x, y) однородная нулевого измерения.
Покажем, что это уравнение можно свести к уравнению с разделенными переменными.
Рассмотрим функцию f (tx, ty). Сделаем замену 

Тогда уравнение (7.10) запишется в виде 
В общем случае переменные в однородном уравнение не разделяются сразу. Но, если ввести вспомогательную неизвестную функцию u = u (x) по формуле

то мы сможем превратить однородное уравнение в уравнение с разделенными переменными.
Из формулы (7.12) найдем y’ = u + xu’ и уравнение 
то есть 

После интегрирования получим 
Отсюда находим выражение для функции u, возвращаемся к переменной y = xu и получим решение однородного уравнения.
Чаще всего не удается найти функцию u явно выраженной, тогда, после интегрирования, в левую часть следует подставить 
В результате получим решение уравнения в неявном виде.
Пример 1. Найти решение однородного уравнения
Решение. Заменой y = xu сведем заданное уравнение к уравнению


Отделяя переменные, найдем




Возвращаясь к переменной y, получим общее решение: 
Линейные дифференциальные уравнения
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое содержит искомую функцию и ее производную в первой степени без их произведения:
y’ + P (x) y = Q (x). (7.13)
Здесь P (x), Q (x) — известные функции независимой переменной x. Например, y’ + 2 xy = x 2 .
Если Q (x) = 0, то уравнение (7.13) называется линейным однородным и является уравнением с разделяющимися переменными.
Если Q (x) ≠ 0, то уравнение (7.13) называется линейным неоднородным, которое можно решить несколькими способами.
Рассмотрим метод Бернулли, с помощью которого уравнение (7.13) можно свести к интегрированию двух дифференциальных уравнений первого порядка с разделяющимися переменными.
Решение дифференциального уравнения (7.13) ищем в виде y = u (x) v (x) или y = uv, (7.14)
где u (x), v (x) — неизвестные функции. Одну из этих функций можно взять произвольную, а другая определяется из уравнения (7.13).
Из равенства y = uv найдем производную y’:
y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение (7.13):
u’v + uv’ + P (x) ⋅ u⋅ v = Q (x) или u’v + u (v’ + P (x) ⋅ v) = Q (x).
Выберем функцию v такой, чтобы v’ + P (x) v = 0. (7.15)
Тогда для отыскания функции u получим уравнение:
u’v = Q (x). (7.16)
Сначала найдем v из уравнения (7.15).
Отделяя переменные, имеем 
Под неопределенным интегралом здесь будем понимать какую-то одну первообразную от функции P (x), то есть v будет определенной функцией от x.
Зная v, находим u из уравнения (7.16): 
откуда
Здесь мы уже берем для u все первообразные.
Найденные функции u и v подставляем в (7.14) и получаем общее решение линейного дифференциального уравнения:

При решении конкретных примеров проще выполнять эти выкладки, чем применять громоздкую формулу (7.17).
Пример 1. Решить дифференциальное уравнение 
Решение. Решение ищем в виде y = uv, тогда y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение: 

Выражение, стоящее в скобках, приравниваем к нулю, имеем

Отделим переменные, домножив обе части уравнения на 

После интегрирования, получим ln |v| = ln |x| (здесь ограничимся одной первообразной), откуда v = x.
Подставим v = x в уравнение (7.18):
Общее решение запишется:
y = x (x + C) = x 2 + Cx.
Пример 2. Найти частное решение дифференциального уравнения 
Решение. Заданное уравнение — это линейное неоднородное уравнение первого порядка, решение которого ищем в виде y = u⋅v.
Тогда 
Подставим v в уравнение и найдем u:
Общее решение дифференциального уравнения будет:
Подставляем начальные условия в найденное решение и находим С:
Из общего решения получаем частное решение 
Дифференциальное уравнение Бернулли
Определение. Уравнения вида


называется дифференциальным уравнением Бернулли.
Данное уравнение отличается от уравнения (7.13) только множителем y» (или x») в правой части. Для того, чтобы права часть данного уравнения была такой, как в (7.13), разделим его левую и праву часть на y»:
Сделаем замену: 
Домножим левую и правую части полученного уравнения на (n + 1) и, используя замену, получим: 
Мы получили линейное дифференциальное уравнение относительно новой переменной
Пример 1. Найти общее решение дифференциального уравнения xy’ + y = y 2 ln x.
Решение. 
Сделаем замену 
Данное уравнение решим, сделав замену z = u (x) ⋅ v (x).
Выбираем функцию v (x) так, чтобы выражение в скобках равнялось нулю, и эта функция была бы частным решением уравнения
Тогда 
Проинтегрировав правую часть этого уравнения по частям, получим 
Обыновенное дефференциальное уравнение
Обыкновенным дифференциальным уравнением называется любое соотношение, связывающее независимую переменную 


Обыкновенное дифференциальное уравнение может быть приведено к виду
Здесь 
Число 
Обыкновенные дифференциальные уравнения первого порядка, разрешенные относительно производной. уравнения, интегрируемые в квадратурах
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Основные понятия и определения
Понятие об уравнении первого порядка, разрешенном относительно производной. В соответствии со сказанным во введении, уравнение первого порядка имеет вид
В этой главе мы будем рассматривать уравнение, разрешенное относительно производной:
Наряду с этим уравнением мы всегда будем рассматривать перевернутое уравнение
используя последнее в окрестности тех точек, в которых 
Во многих случаях оказывается целесообразным «место уравнении (2) и (2′) рассматривать одно равносильное им дифференциальное уравнение
Обе переменные 

Умножая обе части уравнения (3) на некоторую функцию 
где 


Иногда уравнение записывают *з так называемой симметрической форме:
Возможно вам будут полезны данные страницы:
Решение уравнения. Предположим, что правая часть уравнения (2), 




- Существует производная
для всех значений
из интервала
(Отсюда следует, что решение
представляет собою функцию, непрерывную ею всей области определения).
- Функция
обращает уравнение (2) в тождество:
справедливое для всех значений 





Так как наряду с уравнением (2) рассматривается перевернутое уравнение (2′), то и решения 
В этом смысле в дальнейшем мы будем для краткости называть решения уравнения (2′) решениями уравнения (2).
Примеры с решением
Пример 1.
является решением уравнения
в интервале 
справедливое при всех значениях
Пример 2.
Функция 

Пример 3.
является решением уравнения
в интервале
Иногда функцию 
Системы обыкновенных дифференциальных уравнений
При решении многих задач нужно найти функции y1 = y1 (x), y2 = y2 (x), . yn = yn (x), которые удовлетворяют системе дифференциальных уравнений, содержащих независимую переменную x , искомые y1 , y2 , . yn и их производные.
Пример. Пусть материальная точка массы m имеет криволинейную траекторию движения в пространстве. Определить положение точки в любой момент времени t, когда на нее действует сила 
Положение точки в любой момент времени t определяется ее координатами x, y, z; следовательно, x, y, z являются функциями от t. Проекциями вектора скорости точки на оси координат будут производные x’ , y’ , z’.
Положим, что сила

функции определяются из уравнений динамики:
Мы получили систему трех дифференциальных уравнений второго порядка. В случае движения, когда траектория является плоской кривой, лежит, например, в плоскости Оxy, получим систему двух уравнений для определения неизвестных функций x (t) и y (t):
Рассмотрим простейшие системы дифференциальных уравнений.
Системы дифференциальных уравнений первого порядка
Система n уравнений первого порядка с n неизвестными функциями имеет вид:

где x — независимая переменная, y1, y2, . yn — неизвестные функции.
Если в левой части уравнений системы стоят производные первого порядка, а правые части уравнений вовсе не содержат производных, то такая система уравнений называется нормальной.
Решением системы называется совокупность функций y1, y2, . yn, которые превращают каждое уравнение системы в тождество относительно x.
Задача Коши для системы (7.38) состоит в нахождении функций y1, y2, . yn , удовлетворяющих систему (7.38) и заданные начальные условия:

Интегрирование системы (7.38) делают следующим образом. Дифференцируем по x первое уравнение системы (7.38): 
Заменим производные


Дифференцируем полученное уравнение и, подставив в это равенство значения производных из системы (7.38), найдем 
Продолжая дальше таким образом, получим 
В результате получаем следующую систему уравнений:

Из первых (n-1) уравнений определим y2, y3, . yn:

и подставим их значения в последнее уравнение системы (7.40) для определения y1:
Продифференцируем это выражение (n-1) раз, определим


Для того, чтобы полученное решение удовлетворяло заданным начальным условиям, остается только найти значение произвольных постоянных из уравнений (7.42) и (7.43) так, как мы это делали для одного дифференциального уравнения.
Пример 1. Проинтегрировать систему 
когда заданы начальные условия 
Решение. Дифференцируем по x первое уравнение, имеем: 



Из первого уравнения системы найдем 

Общим решением этого уравнения является

и тогда 
Подберем постоянные С1 и С2 так, чтобы выполнялись начальные условия. На основании (*) и (**) имеем:
1 = С1 – 9; 0 = С2 – 2С1 + 14, откуда С1 = 10, С2 = 6.
Таким образом, решением системы, которое удовлетворяет заданным начальным условиям, будет:
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Система дифференциальных уравнений:

где коэффициенты aij — постоянные числа, t — независимая переменная, x1 (t), . xn (t) —
неизвестные функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами.
Эту систему можно решать путем сведения к одному уравнению n-го порядка, как это было показано выше. Но эту систему можно решить и другим способом. Покажем, как это делается.
Будем искать решение системы (7.44) в виде:

Надо определить постоянные α1, α2, . αn и k так, чтобы функции (7.45) удовлетворяли систему (7.44). Подставим функции (7.45) в систему (7.44):
Сократим на e kt и преобразуем систему, сведя ее к такой системе:

Это система линейных алгебраических уравнений относительно α1, α2, . αn. Составим определитель системы:
Мы получим нетривиальные (ненулевые) решения (7.45) только при таких k, при которых определитель превратится в ноль. Получаем уравнение n-го порядка для определения k:
Это уравнение называется характеристическим уравнением для системы (7.44).
Рассмотрим отдельные случаи на примерах:
1) Корни характеристического уравнения действительны и различны. Решение системы записывается в виде:
Пример 2. Найти общее решение системы уравнений:
Решение. Составим характеристическое уравнение:

Решение системы ищем в виде
Составим систему (7.46) для корня k1 и найдем 


Откуда 


Итак, мы получили решение системы:
Далее составляем систему (7.46) для k = 4:
Откуда 
Получим второй решение системы: 
Общее решение системы будет:
2) Корни характеристического уравнения различны, но среди них есть комплексные:
k1 = α + iβ, k2 = α – iβ. Этим корням будут отвечать решения:


Можно доказать также, что истинные и мнимые части комплексного решения также будут решениями. Таким образом, получим два частных решения:

где 

Соответствующие комбинации функций (7.49) войдут в общий решение системы.
Пример 3. Найти общее решение системы
Решение. Составляем характеристическое уравнение:

Подставляем поочередно k1, k2 в систему (7.46), найдем
Запишем уравнение (7.47) и (7.48) для наших данных
Перепишем эти решения в таком виде:
За частные решения можно взять отдельно действительные и отдельно мнимые части:
Общим решением системы будет
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами
Ниже разберем способы, как решить линейные однородные и неоднородные дифференциальные уравнения порядка выше второго, имеющих постоянные коэффициенты. Подобные уравнения представлены записями y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , в которых f 0 , f 1 , . . . , f n — 1 — являются действительными числами, а функция f ( x ) является непрерывной на интервале интегрирования X .
Оговоримся, что аналитическое решение подобных уравнений иногда неосуществимо, тогда используются приближенные методы. Но, конечно, некоторые случаи дают возможность определить общее решение.
Общее решение ЛОДУ и ЛДНУ
Мы зададим формулировку двух теорем, показывающих, какого вида общих решений ЛОДУ и ЛНДУ n -ого порядка следует искать.
Общим решением y 0 ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 на интервале
X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) будет линейная комбинация
n линейно независимых частных решений ЛОДУ y j , j = 1 , 2 , . . . , n , содержащая произвольные постоянные коэффициенты C j , j = 1 , 2 , . . . , n , то есть y 0 = ∑ j = 1 n C j · y j .
Общим решением y ЛНДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) на интервале X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) и функцией f ( x ) будет являться сумма y = y 0 + y
, где y 0 — общее решение соответствующего ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 , а y
— некоторое частное решение исходного ЛНДУ.
Итак, общее решение линейного неоднородного дифференциального уравнения, содержащего постоянные коэффициенты y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , нужно искать, как y = y 0 + y
— некоторое его частное решение, а y 0 = ∑ j = 1 n C j · y j – общее решение соответствующего однородного дифференциального уравнения y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .
В первую очередь рассмотрим, как осуществлять нахождение y 0 = ∑ j = 1 n C j · y j — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами, а потом научимся определять частное решение y
линейного неоднородного дифференциального уравнения n -ого порядка при постоянных коэффициентах.
Алгебраическое уравнение n -ого порядка k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 носит название характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка, содержащего постоянные коэффициенты, записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .
Возможно определить n частных линейно независимых решений y 1 , y 2 , . . . , y n исходного ЛОДУ, исходя из значений найденных n корней характеристического уравнения k 1 , k 2 , . . . , k n .
Методы решения ЛОДУ и ЛНДУ
Укажем все существующие варианты и приведем примеры на каждый.
- Когда все решения k 1 , k 2 , . . . , k n характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 действительны и различны, линейно независимые частные решения будут выглядеть так:
y 1 = e k 1 · x , y 2 = e k 2 · x , . . . , y n = e k n · x . Общее же решение ЛОДУ n -ого порядка при постоянных коэффициентах запишем как: y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x + . . . + C n · e k n · x .
Пример 1
Задано ЛОДУ третьего порядка, содержащее постоянные коэффициенты y ‘ ‘ ‘ — 3 y » — y ‘ + 3 y = 0 . Определите его общее решение.
Решение
Cоставим характеристическое уравнение и найдем его корни, разложив предварительно многочлен из левой части равенства на множители, используя метод группировки:
k 3 — 3 k 2 — k + 3 = 0 k 2 ( k — 3 ) — ( k — 3 ) = 0 ( k 2 — 1 ) ( k — 3 ) = 0 k 1 = — 1 , k 2 = 1 , k 3 = 3
Ответ: найденные корни являются действительными и различными, значит общее решение ЛОДУ третьего порядка с постоянными коэффициентами запишем как: y 0 = C 1 · e — x + C 2 e x + C 3 · e 3 x .
- Когда решения характеристического уравнения являются действительными и одинаковыми ( k 1 = k 2 = . . . = k n = k 0 ) , линейно независимые частные решения линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами буду иметь вид: y 1 = e k 0 · x , y 2 = x · e k 0 · x , . . . , y n = x n — 1 · e k 0 · x .
Общее же решение ЛОДУ будет выглядеть так:
y 0 = C 1 · e k 0 · x + C 2 · e k 0 · x + . . . + C n · x n — 1 · e k 0 · x = = e k 0 · x · C 1 + C 2 · x + . . . + C n · x n — 1
Задано дифференциальное уравнение: y ( 4 ) — 8 k ( 3 ) + 24 y » — 32 y ‘ + 16 y = 0 . Необходимо определить его общее решение.
Решение
Составим характеристическое уравнение заданного ЛОДУ: k 4 — 8 k 3 + 24 k 2 — 32 k + 16 = 0 .
Преобразуем данное характеристическое уравнение, используя формулу бинома Ньютона, оно примет вид: k — 2 4 = 0 . Отсюда мы выделим его четырехкратный корень k 0 = 2 .
Ответ: общим решением заданного ЛОДУ станет: y 0 = e 2 x · C 1 + C 2 · x + C 3 · x 2 + C 4 · x 3
- Когда решения характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка при постоянных коэффициентах — различные комплексно сопряженные пары α 1 ± i · β 1 , α 2 ± i · β 2 , . . . , α m ± i · β m , n = 2 m , линейно независимые частные решения такого ЛОДУ будут иметь вид:
y 1 = e α 1 x · cos β 1 x , y 2 = e α 1 x · sin β 1 x , y 3 = e α 2 x · cos β 2 x , y 4 = e α 2 x · sin β 2 x , … y n — 1 = e α m x · cos β m x , y n = e α m x · sin β m x
Общее же решение запишем так:
y 0 = e α 1 x · C 1 · cos β 1 x + C 2 · sin β 1 x + + e α 2 x · C 3 · cos β 2 x + C 4 · sin β 2 x + . . . + + e α m x · C n — 1 · cos β m x + C n · sin β m x
Задано ЛОДУ четвертого порядка при постоянных коэффициентах y ( 4 ) — 6 y ( 3 ) + 14 y » — 6 y ‘ + 13 y = 0 . Необходимо его проинтегрировать.
Решение
Составим характеристическое уравнение заданного ЛОДУ: k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 . Осуществим преобразования и группировки:
k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 k 4 + k 2 — 6 k 3 + k + 13 k 2 + 1 = 0 k 2 + 1 k 2 — 6 k + 13 = 0
Из полученного результата несложно записать две пары комплексно сопряженных корней k 1 , 2 = ± i и k 3 , 4 = 3 ± 2 · i .
Ответ: общее решение заданного линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами запишется как:
y 0 = e 0 · C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x = = C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x
- Когда решения характеристического уравнения — это совпадающие комплексно сопряженные пары α ± i · β , линейно независимыми частными решениями линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами будут записи:
y 1 = e α · x · cos β x , y 2 = e α · x · sin β x , y 3 = e α · x · x · cos β x , y 4 = e α · x · x · sin β x , … y n — 1 = e α · x · x m — 1 · cos β x , y n = e α · x · x m — 1 · sin β x
Общим решением ЛОДУ будет:
y 0 = e α · x · C 1 · cos β x + C 2 · sin β x + + e α · x · x · C 4 · cos β x + C 3 · sin β x + . . . + + e α · x · x m — 1 · C n — 1 · cos β x + C n · sin β x = = e α · x · cos β x · C 1 + C 3 · x + . . . + C n — 1 · x m — 1 + + e α · x · sin β x · C 2 + C 4 · x + . . . + C n · x m — 1
Задано линейное однородное дифференциальное уравнение с постоянными коэффициентами y ( 4 ) — 4 y ( 3 ) + 14 y » — 20 y ‘ + 25 y = 0 . Необходимо определить его общее решение.
Решение
Составим запись характеристического уравнения, заданного ЛОДУ, и определим его корни:
k 4 — 4 k 3 + 14 k 2 — 20 k + 25 = 0 k 4 — 4 k 3 + 4 k 2 + 10 k 2 — 20 k + 25 = 0 ( k 2 — 2 k ) 2 + 10 ( k 2 — 2 k ) + 25 = 0 ( k 2 — 2 k + 5 ) 2 = 0 D = — 2 2 — 4 · 1 · 5 = — 16 k 1 , 2 = k 3 , 4 = 2 ± — 16 2 = 1 ± 2 · i
Таким образом, решением характеристического уравнения будет двукратная комплексно сопряженная пара α ± β · i = 1 ± 2 · i .
Ответ: общее решение заданного ЛОДУ: y 0 = e x · cos 2 x · ( C 1 + C 3 · x ) + e x · sin 2 x · ( C 2 + C 4 · x )
- Встречаются различные комбинации указанных случаев: некоторые корни характеристического уравнения ЛОДУ n -ого порядка с постоянными коэффициентами являются действительными и различными, некоторые — действительными и совпадающими, а какие-то — комплексно сопряженными парами или совпадающими комплексно сопряженными парами.
Пример 5
Задано дифференциальное уравнение y ( 5 ) — 9 y ( 4 ) + 41 ( 3 ) + 35 y » — 424 y ‘ + 492 y = 0 . Необходимо определить его общее решение.
Решение
Составим характеристическое уравнение заданного ЛОДУ: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = 0 .
Левая часть содержит многочлен, который возможно разложить на множители. В числе делителей свободного члена определяем двукратный корень k 1 = k 2 = 2 и корень k 3 = — 3 .
На основе схемы Горнера получим разложение: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = k + 3 k — 2 2 k 2 — 8 k + 41 .
Квадратное уравнение k 2 — 8 k + 41 = 0 дает нам оставшиеся корни k 4 , 5 = 4 ± 5 · i .
Ответ: общим решением заданного ЛОДУ с постоянными коэффициентами будет: y 0 = e 2 x · C 1 + C 2 x + C 3 · e — 3 x + e 4 x · C 4 · cos 5 x + C 5 · sin 5 x
Таким образом, мы рассмотрели основные случаи, когда возможно определить y 0 — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами.
Следующее, что мы разберем – это ответ на вопрос, как решить линейное неоднородное дифференциальное уравнение n -ого порядка с постоянными коэффициентами записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) .
Общее решение в таком случае составляется как сумма общего решения соответствующего ЛОДУ и частного решения исходного ЛНДУ: y = y 0 + y
. Поскольку мы уже умеем определять y 0 , остается разобраться с нахождением y
, т.е. частного решения ЛНДУ порядка n с постоянными коэффициентами.
Приведем все способы нахождения y
согласно тому, какой вид имеет функция f ( x ) , находящаяся в правой части рассматриваемого ЛНДУ.
- Когда f ( x ) представлена в виде многочлена n -ой степени f ( x ) = P n ( x ) , частным решением ЛНДУ станет: y
= Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом степени n , а r – указывает, сколько корней характеристического уравнения равно нулю.
Когда функция f ( x ) представлена в виде произведения многочлена степени n и экспоненты f ( x ) = P n ( x ) · e α · x , частным решением ЛНДУ второго порядка станет: y
= e α · x · Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом n —ой степени, r указывает, сколько корней характеристического уравнения равно α .
Когда функция f ( x ) записана как f ( x ) = A 1 cos ( β x ) + B 1 sin ( β x ) , где А 1 и В 1 – числа, частным решением ЛНДУ станет запись y
= A cos β x + B sin β x · x γ . Здесь где А и В являются неопределенными коэффициентами, r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно ± i β .
Когда f ( x ) = e α x · P n ( x ) sin β x + Q k x cos β x , то y
= e α x · L m x sin β x + N m x cos β x · x γ , где r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно α ± i β , P n ( x ) , Q k ( x ) , L m ( x ) и N m ( x ) являются многочленами степени n , k , m и m соответственно, m = m a x ( n , k ) .
Коэффициенты, которые неизвестны, определяются из равенства y
( n — 1 ) + . . . + f 1 y
Подробности нахождения решений уравнений в каждом из указанных случаев можно изучить в статье линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, поскольку схемы решения ЛНДУ степени выше второй полностью совпадают.
Когда функция f ( x ) имеет любой иной вид, общее решение ЛНДУ возможно определить, используя метод вариации произвольных постоянных. Его разберем подробнее.
Пусть нам заданы y j , j = 1 , 2 , . . . , n — n линейно независимые частные решения соответствующего ЛОДУ, тогда, используя различные вариации произвольных постоянных, общим решением ЛНДУ
n -ого порядка с постоянными коэффициентами будет запись: н = ∑ j = 1 n C j ( x ) · y j . В нахождении производных функций C j ( x ) , j = 1 , 2 , . . . , n поможет система уравнений:
∑ j = 1 n C j ‘ ( x ) · y j = 0 ∑ j = 1 n C j ‘ ( x ) · y ‘ j = 0 ∑ j = 1 n C j ‘ ( x ) · y » j = 0 … ∑ j = 1 n C j ‘ ( x ) · y j ( n — 2 ) = 0 ∑ j = 1 n C j ‘ ( x ) · y j ( n — 1 ) = 0
а собственно функции C j ( x ) , j = 1 , 2 , . . . , n найдем при последующем интегрировании.
Задано ЛНДУ с постоянными коэффициентами: y ‘ ‘ ‘ — 5 y » + 6 y ‘ = 2 x . Необходимо найти его общее решение.
Решение
Составим характеристическое уравнение: k 3 — 5 k 2 + 6 k = 0 . Корни данного уравнения: k 1 = 0 , k 2 = 2 и k 3 = 3 . Таким образом, общим решением ЛОДУ будет запись: y 0 = C 1 + C 2 · e 2 x + C 3 · e 3 x , а частные линейно независимые решения это: y 1 = 1 , y 2 = e 2 x , y 3 = e 3 x .
Варьируем произвольные постоянные: y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x .
Чтобы определить C 1 ( x ) , C 2 ( x ) и C 3 ( x ) , составим систему уравнений:
C ‘ 1 ( x ) · y 1 + C ‘ 2 ( x ) · y 2 + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · y ‘ 1 + C ‘ 2 ( x ) · y ‘ 2 + C ‘ 3 ( x ) · y ‘ 3 = 0 C ‘ 1 ( x ) · y » 1 + C ‘ 2 ( x ) · y » 2 + C ‘ 3 ( x ) · y » 3 = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · 1 ‘ + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · e 3 x ‘ = 0 C ‘ 1 ( x ) · 1 ‘ ‘ + C ‘ 2 x · e 2 x ‘ ‘ + C ‘ 3 ( x ) · e 3 x ‘ ‘ = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x + C ‘ 3 ( x ) · e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 2 e 2 x + C ‘ 3 ( x ) · 3 e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 4 e 2 x + C ‘ 3 ( x ) · 9 e 3 x = 2 x
Решаем, используя метод Крамера:
∆ = 1 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 0 4 e 2 x 9 e 3 x = 18 e 2 x · e 3 x — 12 e 2 x · e 3 x = 6 e 5 x ∆ C 1 ‘ ( x ) = 0 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 2 x 4 e 2 x 9 e 3 x = e 5 x · 2 x ⇒ C ‘ 1 ( x ) = ∆ C 1 ‘ ( x ) ∆ = e 5 x · 2 x 6 e 5 x = 1 6 · 2 x ∆ C 2 ‘ ( x ) = 1 0 e 3 x 0 0 3 e 3 x 0 2 x 9 e 3 x = — 3 e x · 2 x ⇒ C ‘ 2 ( x ) = ∆ C 2 ‘ ( x ) ∆ = — 3 e 3 x · 2 x 6 e 5 x = — 1 2 · e — 2 x · 2 x ∆ C 3 ‘ ( x ) = 1 e 2 x 0 0 2 e 2 x 0 0 4 e 2 x 2 x = 2 e 2 x · 2 x ⇒ C ‘ 3 ( x ) = ∆ C 3 ‘ ( x ) ∆ = 2 e 2 x · 2 x 6 e 5 x = 1 3 · e — 3 x · 2 x
Интегрируем C ‘ 1 ( x ) = 1 6 · 2 x с помощью таблицы первообразных, а
C ‘ 2 ( x ) = — 1 2 · e — 2 x · 2 x и C ‘ 3 ( x ) = 1 3 · e — 3 x · 2 x при помощи метода интегрирования по частям, получим:
C 1 ( x ) = 1 6 · ∫ 2 x d x = 1 6 · 2 x ln 2 + C 4 C 2 ( x ) = — 1 2 · ∫ e — 2 x · 2 x d x = — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 C 3 ( x ) = 1 3 · ∫ e — 3 x · 2 x d x = 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6
Ответ: искомым общим решением заданного ЛОДУ с постоянными коэффициентами будет:
y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x = = 1 6 · 2 x ln 2 + C 4 + — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 · e 2 x + + 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6 · e 3 x
где C 4 , C 5 и C 6 – произвольные постоянные.
http://natalibrilenova.ru/obyiknovennyie-differentsialnyie-uravneniya/
http://zaochnik.com/spravochnik/matematika/differentsialnye-uravnenija/linejnye-differentsialnye-uravnenija-vysshih-por-1/
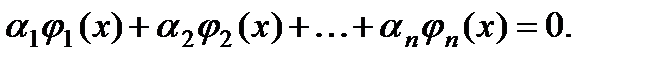
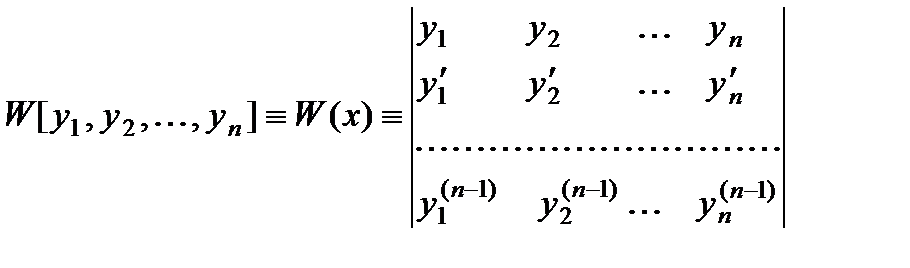

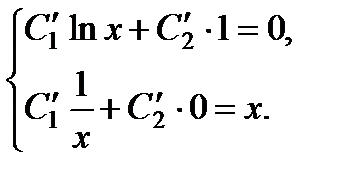
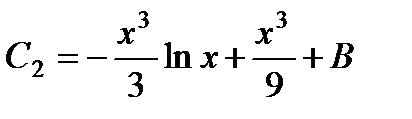
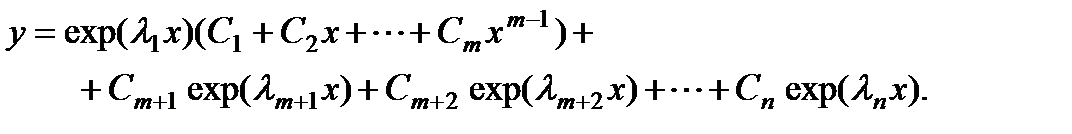

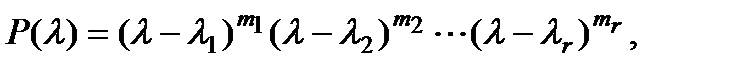
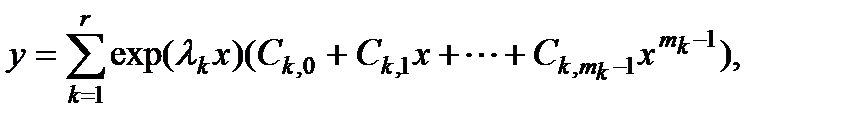
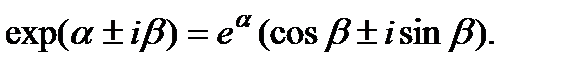
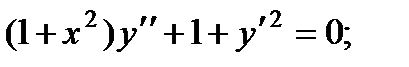
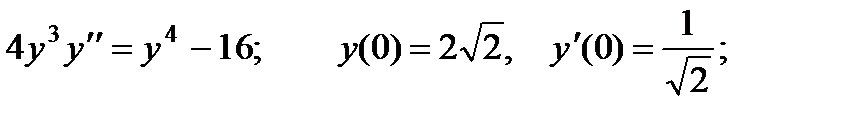
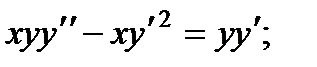
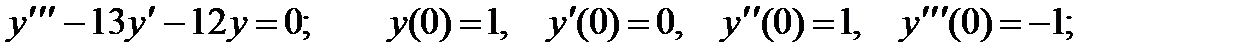
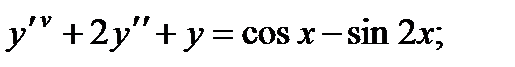
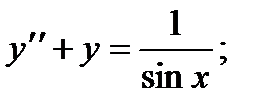

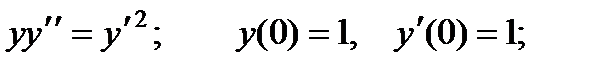
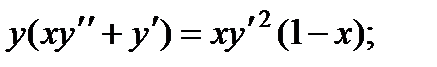
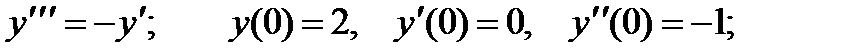
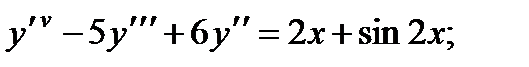
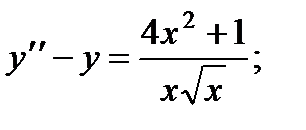

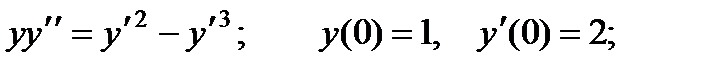
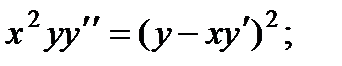

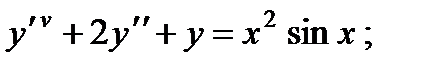
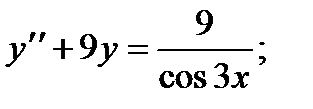
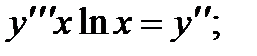
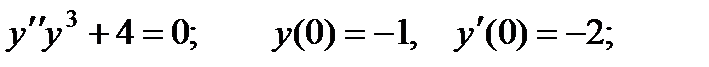
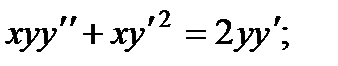

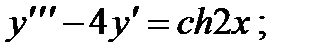
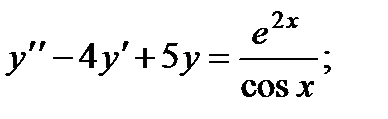

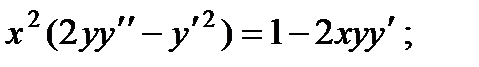
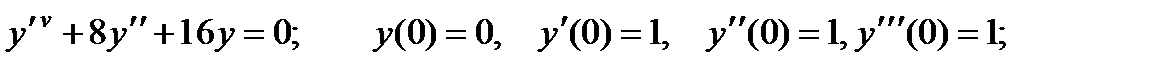
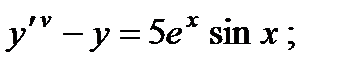
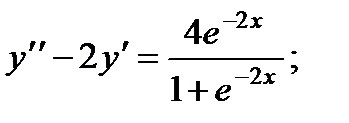
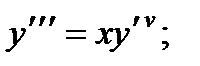
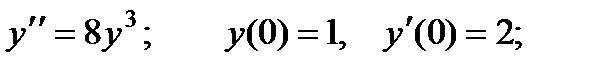
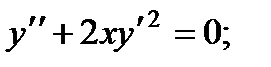
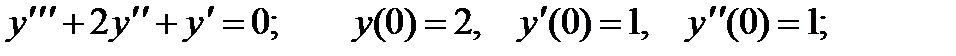
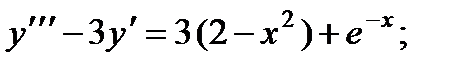
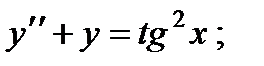
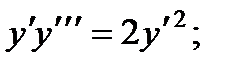
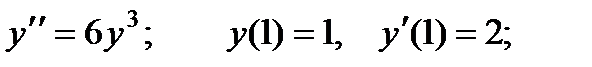


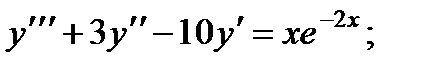
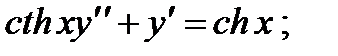
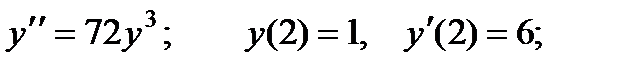
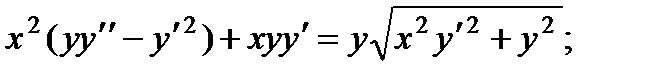
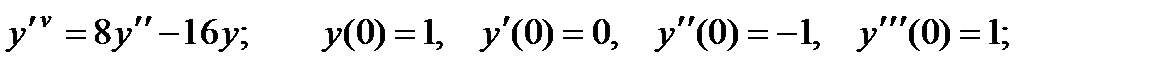
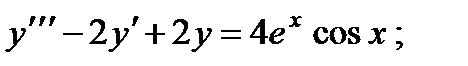


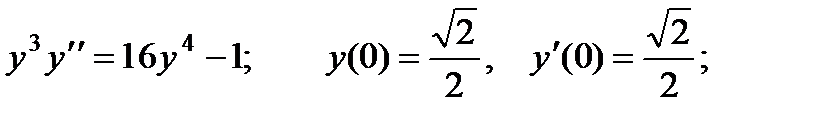
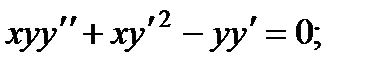
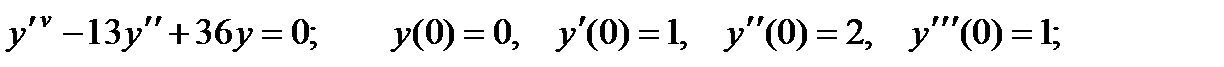
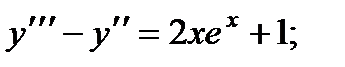
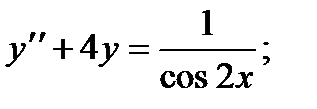
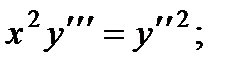
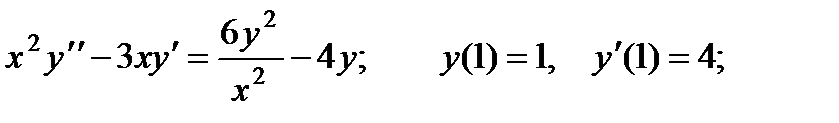
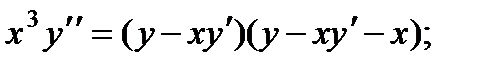
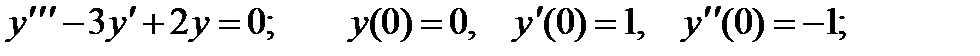
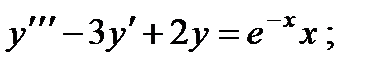
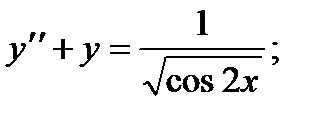
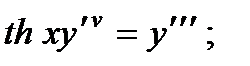
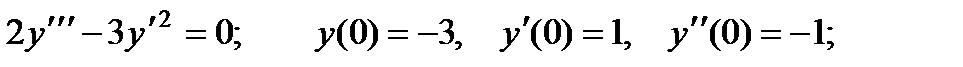
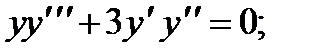
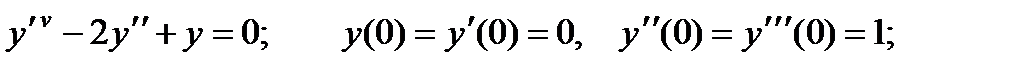
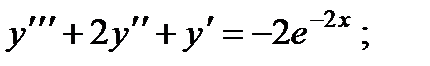
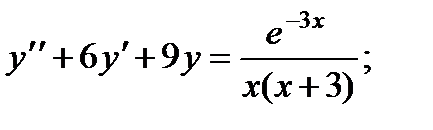
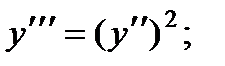
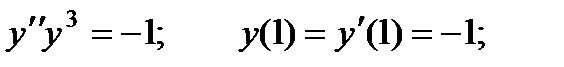
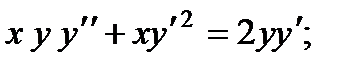
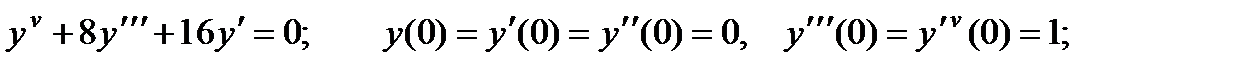
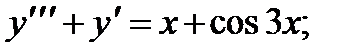
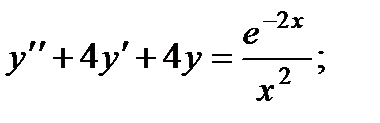
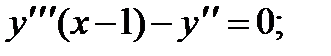

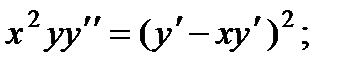
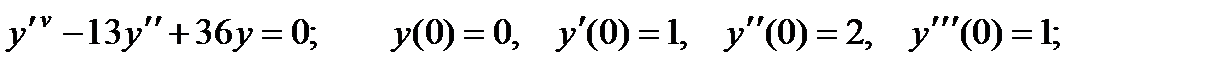

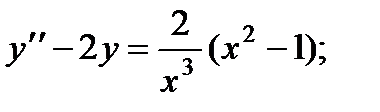
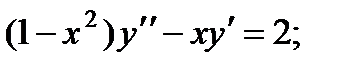
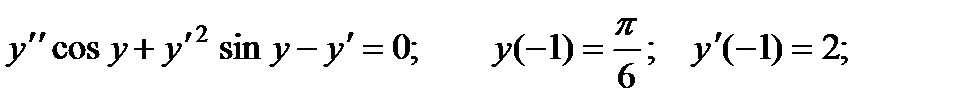

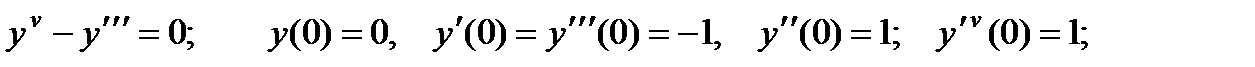
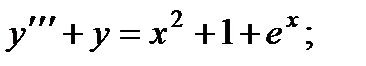

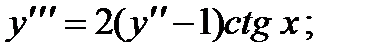
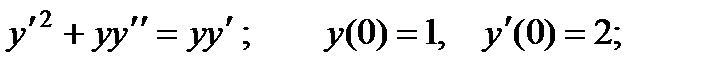

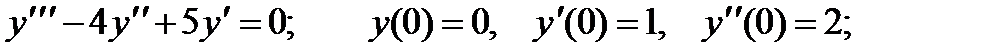
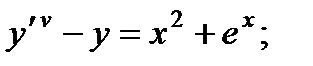

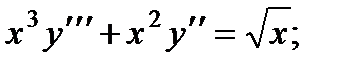

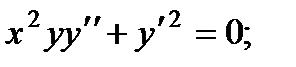
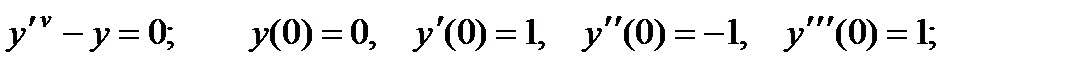
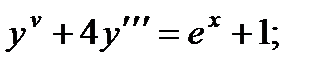
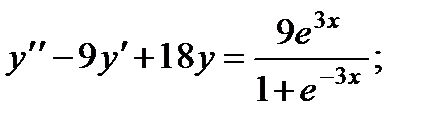
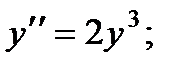

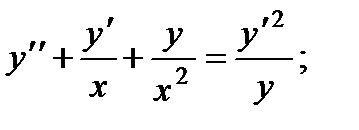

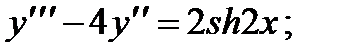
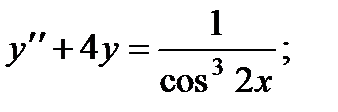
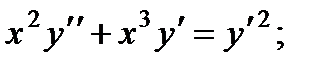
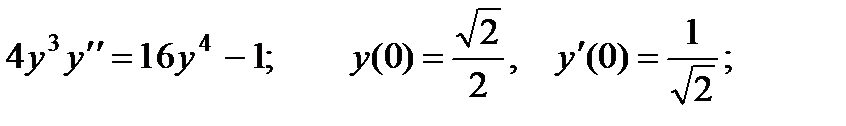
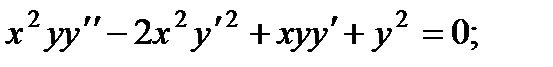

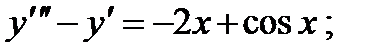
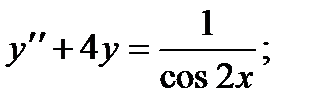
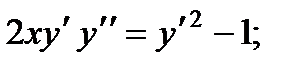



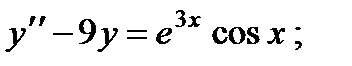
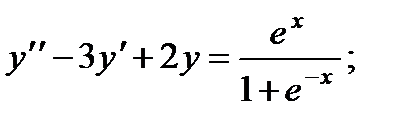


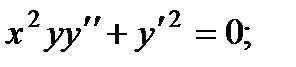

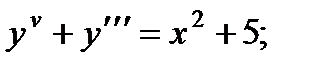
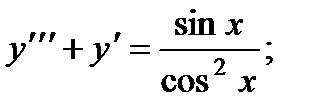

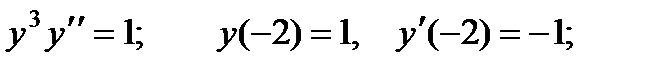
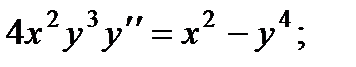
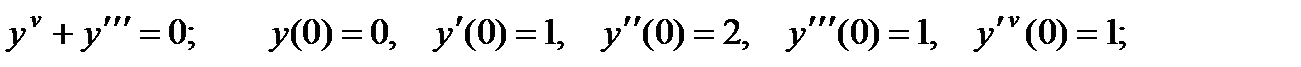
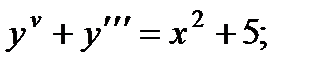
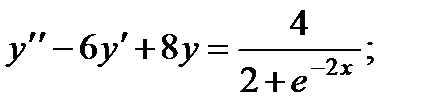
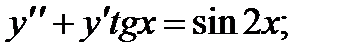
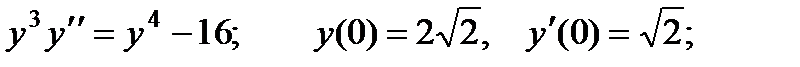
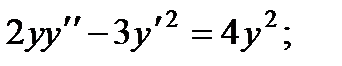
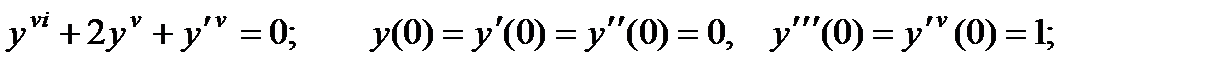

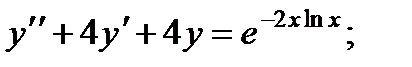


































 для всех значений
для всех значений  из интервала
из интервала  (Отсюда следует, что решение
(Отсюда следует, что решение  представляет собою функцию, непрерывную ею всей области определения).
представляет собою функцию, непрерывную ею всей области определения). обращает уравнение (2) в тождество:
обращает уравнение (2) в тождество: 


































