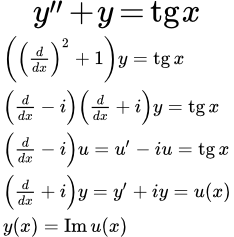Линейные дифференциальные уравнения с комплексными коэффициентами

Пример комплексной подстановки при решении линейного неоднородного дифференциального уравнения

Метод понижения порядка линейного неоднородного дифференциального уравнения с комплексными корнями характеристического уравнения

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) .
Мы полагаем, что коэффициенты этого уравнения являются действительными числами. Здесь мы рассматриваем случай, когда характеристическое уравнение
(2)
имеет комплексные корни.

Для решения уравнения (1), применим метод понижения порядка. Поскольку коэффициенты характеристического уравнения (2) являются действительными числами, то его комплексные корни являются попарно комплексно сопряженными. Пусть – два комплексно сопряженные корня: . Запишем исходное уравнение (1) в следующем виде:
(3) ,
где – оператор дифференцирования.

Обозначим:
.
Тогда уравнение (3) принимает следующий вид:
.
Сделаем подстановку:
(4) .
Получаем уравнение первого порядка с комплексным коэффициентом :
.
Или
(5) .
Решение этого уравнения имеет следующий вид (см. страницу метод понижения порядка ):
,
где – комплексная постоянная.

Далее замечаем, что поскольку исходное уравнение (1) имеет действительные коэффициенты, то переменная u и ее производная u′ должны быть действительными. Выразим комплексный корень через действительную и мнимую части:
.
Подставим в (4):
.
Извлекая мнимую часть, получаем:
.
Отсюда
.

Таким образом, в случае с комплексными корнями, один этап решения приводит к понижению порядка на две единицы.

Пример решения дифференциального уравнения

Решить уравнение
(П1) .

Перепишем уравнение в следующем виде:
.
Вводим обозначение :
.

Характеристическое уравнение

имеет комплексные корни: . Тогда
.

Переписываем исходное уравнение:
;
.
Делаем подстановку:
;
(П2) .
Тогда уравнение принимает вид:
;
(П3) .

Это линейное неоднородное дифференциальное уравнение первого порядка. Ищем решение с помощью интегрирующего множителя. Умножим на и выполняем преобразования:
;
;
(П4) ,
где – комплексная постоянная; – действительные постоянные.

Вычисляем интеграл в (П4) с помощью подстановки .

.

Выразим арктангенс через логарифм, используя уравнение: .
;
.
Отсюда
(П5) .

Теперь в правой части (П6) нам нужно отделить вещественную и мнимую части. Мнимая часть уравнения (П6) и даст искомое решение y .

Для преобразования логарифма, используем формулу: . Далее замечаем, что . Тогда при имеем:
.
При :
.
Оба случая можно записать одной формулой:
,
где при нужно взять верхний знак ′+′; при – нижний знак ′–′.

Подставим в (П6) и выполним преобразования:
;
.
Переобозначим постоянную :
(П7) .

Теперь преобразуем экспоненту с помощью формулы Эйлера: , и выразим комплексную постоянную через действительную и мнимую части: . Подставляем в (П7):
.
Выполняем преобразования:

.
Тогда

.
Отделяем мнимую часть:

.

Автор: Олег Одинцов . Опубликовано: 20-07-2013 Изменено: 26-08-2020

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Дифференциальные уравнения
• Высшая математика.
• Комплексные числа

Комплексные числа

Действия над комплексными числами.

Комплексные числа — числа вида $x+iy,$ где $x,y\in \mathbb$ а
$\,i,$ такое число, что $ i^2=-1.$ Множество комплексных чисел
обозначается $\mathbb.$

Действия над комплексными числами.

Сложение комплексных чисел:

Умножение двух комплексных чисел:

Умножение комплексного числа на действительное:

$$\lambda(x+iy)=\lambda x+i\lambda y.$$

Деление комплексных чисел:

Действительные числа $x$ и $y$ комплексного числа $z=x+iy,$ называются действительной и мнимой частью числа $z$ и обозначаются, соответственно, $Re z=x$ и $Im z=y.$

Два комплексных числа $z_1=x_1+iy_1$ и $z_2=x_2+iy_2$ называются равными в том и только том случае, если $x_1=x_2,$ $y_1=y_2.$

Запись $z=x+iy$ называют алгебраической формой комплексного числа $z.$

Числа $z_1=x+iy$ и $z_2=x-iy$ называют сопряженными.

Примеры:

Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:

1.421. $(2+3i)(3-i).$

Решение:

Ответ: $9+7i.$

1.424. $(2i-i^2)^2+(1-3i)^3.$

Решение.

Ответ: $24+22i.$

Решение.

Ответ: $\frac<1><2>-\frac<3><2>i.$

Решение.

Ответ: $\frac<14><5>i.$

Найти действительные решения следующего уравнения:

1. 430. $(1+i)x+(-2+5i)y=-4+17i.$

Решение.

Ответ: $x=2; y=3.$

Домашнее задание.

Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:

1.422. $(1+2i)^2.$

Ответ: $-3+4i.$

1.423. $(1-i)^3-(1+i)^3.$

1.427. $\left(\frac<1-i><1+i>\right)^3.$

Найти действительные решения следующего уравнения:

1.431. $12((2x+i)(1+i)+(x+y)(3-2i))=17+6i.$

Решить следующие системы линейных уравнений:

1.432. $(3-i)z_1+(4+2i)z_2=1+3i;$

$(4+2i)z_1-(2+3i)z_2=7.$

1.433. $(2+i)z_1+(2-i)z_2=6;$

$(3+2i)z_1+(3-2i)z_2=8.$

Геометрическая интерпретация комплексных чисел.

Множество действительных чисел можно рассматривать как подмножество комплексных чисел, у которых $Im z = 0.$

Можно также изображать комплексное число в виде радиус-вектора $\$ и определять его, задавая его длину $r$ и угол $\varphi$ между осью $Ox$ и вектором.

Длина этого вектора называется модулем комплексного числа $$|z|=r=\sqrt\geq 0,$$ а угол $\varphi$ называется аргументом комплексного числа и обозначается $Arg z.$ Аргумент определяется с точностью до слагаемого $2\pi k\,\,\,\,\, (k=0, \pm 1, \pm 2, \pm 3, . )$ и для положительных значений отсчитывается от оси $Ox$ до вектора против часовой стрелки, а для отрицательных значений – по часовой стрелке.

Значение аргумента, который принадлежит интервалу $(-\pi, \pi],$ называется главным значением аргумента и определяется $arg z.$ Главное значение аргументу числа $x+iy$ можно вычислять по формуле $\varphi= arg z=arctg\left(\frac\right)+k\pi,$ где $k=0,$ если $z$ находится в первой или четвертой четвертях, $k=1,$ если $z$ находится во второй четверти, $k=-1,$ если $z$ находится в третей четверти. Если $x=Rez=0,$ то $\varphi=\pi/2,$ когда $y=Imz>0$ и $\varphi=-\pi/2,$ когда $y=Imz плоскость называется комплексной плоскостью C (рисунок 1), ось $Ox$ называется действительной осью, а ось $Oy$ – мнимой осью. Таким образом, действительному числу $z=x+0i=x$ отвечает точка на действительной оси, а мнимому числу $z=0+iy=y -$ точка на мнимой оси.

Формулы Эйлера и Муавра. Корень n-й степени с комплексного числа.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Формулы Эйлера:

Формула Муавра:

Если $z=re^, $ то $$z^n=r^ne^,$$ или, в тригонометричской форме:

$$z^n=r^n(\cos n\varphi+i\sin n\varphi).$$

Пусть $a=re^, \,\, a\neq 0,-$ фиксированное комплексное число. Тогда уравнение $z^n=a,\,\,\, n\in N,$ имеет в точности $n$ различных решений $z_0, z_1, . z_$ причем эти решения даются формулой $$z_k=\sqrt[n]e^+\frac<2\pi>k\right)>=\sqrt[n]\left(\cos\frac<\varphi+2\pi k>+i\sin\frac<\varphi+2\pi k>\right),$$ $$k=0, 1, . , n-1.$$ (здесь $\sqrt r$ действительное положительное число) Числа $z_k, \,\, k=0, 1, . n-1,$ называются корнями $n-$й степени из комплексного числа $a$ и обозначаются символом $\sqrt[n].$

Примеры:

1.483. Доказать формулу Эйлера $\cos\varphi=\frac+e^<-i\varphi>><2>.$

Решение.

Известно, что $e^=\cos<\varphi>+i\sin\varphi.$ Соответственно, $e^<-i\varphi>=\cos<(-\varphi)>+i\sin(-\varphi)=\cos\varphi-i\sin\varphi.$

Отсюда находим $e^+e^<-i\varphi>=\cos\varphi+i\sin\varphi+\cos\varphi-i\sin\varphi=2\cos\varphi.$

Cледовательно, $\cos\varphi=\frac+e^<-i\varphi>><2>.$ Что и требовалось доказать.

Используя формулу Муавра, вычислить следующие выражения:

1.485. $(1+i)^<10>.$

Решение.

Запишем число $z=1+i$ в показательной форме:

Поскольку число $z$ находится в первой четверти, то

Таким образом, мы можем записать число $z=1+i$ в показательной форме: $z=\sqrt 2 e^<4>>.$

Теперь, используя формулу Муавра можно найти $z^<10>:$

Ответ: $(1+i)^<10>=32i.$

1.491. Используя формулу Муавра, выразить через $\cos\varphi$ и $\sin\varphi$ функцию$\cos 3\varphi.$

Решение.

$$+\left.\cos^3(-\varphi)-3i\cos^2(-\varphi)\sin(-\varphi)+3i^2\cos(-\varphi)\sin^2(-\varphi)-i^3\sin^3(-\varphi)\right)=$$ $$=\frac<1><2>\left(\cos^3<\varphi>+3i(1-\sin^2\varphi)\sin\varphi-3\cos\varphi(1-\cos^2\varphi)\right.-i\sin^3\varphi+$$ $$+\left.\cos^3\varphi+3i(1-\sin^2\varphi)\sin\varphi-3\cos\varphi(1-\cos^2\varphi)-i\sin^3\varphi\right)=$$ $$=\cos^3\varphi+3i\sin\varphi-3i\sin^3\varphi-3\cos\varphi+3\cos^3\varphi-i\sin^3\varphi=$$ $$=4\cos^3\varphi-3\cos\varphi+3i\sin\varphi-4i\sin^3\varphi.$$

Ответ: $4\cos^3\varphi-3\cos\varphi+3i\sin\varphi-4i\sin^3\varphi.$

1.495. Найти и изобразить на комплексной плоскости все корни 2-й, 3-й и 4-й степени из единицы.

Решение.

Запишем число 1 в показательной форме:

$1=1e^<0i>.$ То есть $r=1, \varphi=0.$

Далее, пользуясь формулой Муавра вычисляем корень второй степени из единицы:

Вычисляем корень третьей степени из единицы:

Вычисляем корень четвертой степени из единицы:

Ответ: Корни второй степени: $z_0=1;\,\, z_1 =-1.$ Корни третьей сепени: $z_0=1;\,\, z_1=-\frac<1><2>+i\frac<\sqrt 3><2>;\,\, z_2=-\frac<1><2>-i\frac<\sqrt 3><2>.$ Корни четвертой степени: $z_0=1;\,\, z_1=i;\,\, z_2=-1;\,\, z_3=-i.$

Найти все значения корней:

Решение.

Запишем число $z=-1+i\sqrt 3$ в показательной форме:

Поскольку число $z$ находится во второй четверти, то

Таким образом, мы можем записать число $z=-1+i\sqrt 3$ в показательной форме: $z=2 e^<3>>.$

Пользуясь формулой Муавра вычисляем корень второй степени из единицы:

Ответ: $\pm\frac<\sqrt 2><2>(1+i\sqrt 3)$

1.501. $\sqrt [5]<-1-i>.$

Решение.

Запишем число $z=-1-i 3$ в показательной форме:

Поскольку число $z$ находится в третьей четверти, то

Таким образом, мы можем записать число $z=-1-i$ в показательной форме: $z=\sqrt 2 e^<4>>.$

Пользуясь формулой Муавра вычисляем корень второй степени из единицы:

1.483. Доказать формулу Эйлера $\sin\varphi=\frac-e^<-i\varphi>><2i>.$

Используя формулу Муавра, вычислить следующие выражения:

Используя формулу Муавра, выразить через $\cos\varphi$ и $\sin\varphi$ следующие функции:

Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами

Ниже разберем способы, как решить линейные однородные и неоднородные дифференциальные уравнения порядка выше второго, имеющих постоянные коэффициенты. Подобные уравнения представлены записями y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , в которых f 0 , f 1 , . . . , f n — 1 — являются действительными числами, а функция f ( x ) является непрерывной на интервале интегрирования X .

Оговоримся, что аналитическое решение подобных уравнений иногда неосуществимо, тогда используются приближенные методы. Но, конечно, некоторые случаи дают возможность определить общее решение.

Общее решение ЛОДУ и ЛДНУ

Мы зададим формулировку двух теорем, показывающих, какого вида общих решений ЛОДУ и ЛНДУ n -ого порядка следует искать.

Общим решением y 0 ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 на интервале
X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) будет линейная комбинация
n линейно независимых частных решений ЛОДУ y j , j = 1 , 2 , . . . , n , содержащая произвольные постоянные коэффициенты C j , j = 1 , 2 , . . . , n , то есть y 0 = ∑ j = 1 n C j · y j .

Общим решением y ЛНДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) на интервале X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) и функцией f ( x ) будет являться сумма y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 , а y

— некоторое частное решение исходного ЛНДУ.

Итак, общее решение линейного неоднородного дифференциального уравнения, содержащего постоянные коэффициенты y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , нужно искать, как y = y 0 + y

— некоторое его частное решение, а y 0 = ∑ j = 1 n C j · y j – общее решение соответствующего однородного дифференциального уравнения y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .

В первую очередь рассмотрим, как осуществлять нахождение y 0 = ∑ j = 1 n C j · y j — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами, а потом научимся определять частное решение y

линейного неоднородного дифференциального уравнения n -ого порядка при постоянных коэффициентах.

Алгебраическое уравнение n -ого порядка k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 носит название характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка, содержащего постоянные коэффициенты, записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .

Возможно определить n частных линейно независимых решений y 1 , y 2 , . . . , y n исходного ЛОДУ, исходя из значений найденных n корней характеристического уравнения k 1 , k 2 , . . . , k n .

Методы решения ЛОДУ и ЛНДУ

Укажем все существующие варианты и приведем примеры на каждый.

1. Когда все решения k 1 , k 2 , . . . , k n характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 действительны и различны, линейно независимые частные решения будут выглядеть так:
   y 1 = e k 1 · x , y 2 = e k 2 · x , . . . , y n = e k n · x . Общее же решение ЛОДУ n -ого порядка при постоянных коэффициентах запишем как: y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x + . . . + C n · e k n · x .

Пример 1

Задано ЛОДУ третьего порядка, содержащее постоянные коэффициенты y ‘ ‘ ‘ — 3 y » — y ‘ + 3 y = 0 . Определите его общее решение.

Решение

Cоставим характеристическое уравнение и найдем его корни, разложив предварительно многочлен из левой части равенства на множители, используя метод группировки:
k 3 — 3 k 2 — k + 3 = 0 k 2 ( k — 3 ) — ( k — 3 ) = 0 ( k 2 — 1 ) ( k — 3 ) = 0 k 1 = — 1 , k 2 = 1 , k 3 = 3

Ответ: найденные корни являются действительными и различными, значит общее решение ЛОДУ третьего порядка с постоянными коэффициентами запишем как: y 0 = C 1 · e — x + C 2 e x + C 3 · e 3 x .

1. Когда решения характеристического уравнения являются действительными и одинаковыми ( k 1 = k 2 = . . . = k n = k 0 ) , линейно независимые частные решения линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами буду иметь вид: y 1 = e k 0 · x , y 2 = x · e k 0 · x , . . . , y n = x n — 1 · e k 0 · x .

Общее же решение ЛОДУ будет выглядеть так:
y 0 = C 1 · e k 0 · x + C 2 · e k 0 · x + . . . + C n · x n — 1 · e k 0 · x = = e k 0 · x · C 1 + C 2 · x + . . . + C n · x n — 1

Задано дифференциальное уравнение: y ( 4 ) — 8 k ( 3 ) + 24 y » — 32 y ‘ + 16 y = 0 . Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 4 — 8 k 3 + 24 k 2 — 32 k + 16 = 0 .

Преобразуем данное характеристическое уравнение, используя формулу бинома Ньютона, оно примет вид: k — 2 4 = 0 . Отсюда мы выделим его четырехкратный корень k 0 = 2 .

Ответ: общим решением заданного ЛОДУ станет: y 0 = e 2 x · C 1 + C 2 · x + C 3 · x 2 + C 4 · x 3

1. Когда решения характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка при постоянных коэффициентах — различные комплексно сопряженные пары α 1 ± i · β 1 , α 2 ± i · β 2 , . . . , α m ± i · β m , n = 2 m , линейно независимые частные решения такого ЛОДУ будут иметь вид:
   y 1 = e α 1 x · cos β 1 x , y 2 = e α 1 x · sin β 1 x , y 3 = e α 2 x · cos β 2 x , y 4 = e α 2 x · sin β 2 x , … y n — 1 = e α m x · cos β m x , y n = e α m x · sin β m x

Общее же решение запишем так:

y 0 = e α 1 x · C 1 · cos β 1 x + C 2 · sin β 1 x + + e α 2 x · C 3 · cos β 2 x + C 4 · sin β 2 x + . . . + + e α m x · C n — 1 · cos β m x + C n · sin β m x

Задано ЛОДУ четвертого порядка при постоянных коэффициентах y ( 4 ) — 6 y ( 3 ) + 14 y » — 6 y ‘ + 13 y = 0 . Необходимо его проинтегрировать.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 . Осуществим преобразования и группировки:

k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 k 4 + k 2 — 6 k 3 + k + 13 k 2 + 1 = 0 k 2 + 1 k 2 — 6 k + 13 = 0

Из полученного результата несложно записать две пары комплексно сопряженных корней k 1 , 2 = ± i и k 3 , 4 = 3 ± 2 · i .

Ответ: общее решение заданного линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами запишется как:
y 0 = e 0 · C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x = = C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x

1. Когда решения характеристического уравнения — это совпадающие комплексно сопряженные пары α ± i · β , линейно независимыми частными решениями линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами будут записи:
   y 1 = e α · x · cos β x , y 2 = e α · x · sin β x , y 3 = e α · x · x · cos β x , y 4 = e α · x · x · sin β x , … y n — 1 = e α · x · x m — 1 · cos β x , y n = e α · x · x m — 1 · sin β x

Общим решением ЛОДУ будет:

y 0 = e α · x · C 1 · cos β x + C 2 · sin β x + + e α · x · x · C 4 · cos β x + C 3 · sin β x + . . . + + e α · x · x m — 1 · C n — 1 · cos β x + C n · sin β x = = e α · x · cos β x · C 1 + C 3 · x + . . . + C n — 1 · x m — 1 + + e α · x · sin β x · C 2 + C 4 · x + . . . + C n · x m — 1

Задано линейное однородное дифференциальное уравнение с постоянными коэффициентами y ( 4 ) — 4 y ( 3 ) + 14 y » — 20 y ‘ + 25 y = 0 . Необходимо определить его общее решение.

Решение

Составим запись характеристического уравнения, заданного ЛОДУ, и определим его корни:

k 4 — 4 k 3 + 14 k 2 — 20 k + 25 = 0 k 4 — 4 k 3 + 4 k 2 + 10 k 2 — 20 k + 25 = 0 ( k 2 — 2 k ) 2 + 10 ( k 2 — 2 k ) + 25 = 0 ( k 2 — 2 k + 5 ) 2 = 0 D = — 2 2 — 4 · 1 · 5 = — 16 k 1 , 2 = k 3 , 4 = 2 ± — 16 2 = 1 ± 2 · i

Таким образом, решением характеристического уравнения будет двукратная комплексно сопряженная пара α ± β · i = 1 ± 2 · i .

Ответ: общее решение заданного ЛОДУ: y 0 = e x · cos 2 x · ( C 1 + C 3 · x ) + e x · sin 2 x · ( C 2 + C 4 · x )

1. Встречаются различные комбинации указанных случаев: некоторые корни характеристического уравнения ЛОДУ n -ого порядка с постоянными коэффициентами являются действительными и различными, некоторые — действительными и совпадающими, а какие-то — комплексно сопряженными парами или совпадающими комплексно сопряженными парами.

Пример 5

Задано дифференциальное уравнение y ( 5 ) — 9 y ( 4 ) + 41 ( 3 ) + 35 y » — 424 y ‘ + 492 y = 0 . Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = 0 .

Левая часть содержит многочлен, который возможно разложить на множители. В числе делителей свободного члена определяем двукратный корень k 1 = k 2 = 2 и корень k 3 = — 3 .

На основе схемы Горнера получим разложение: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = k + 3 k — 2 2 k 2 — 8 k + 41 .

Квадратное уравнение k 2 — 8 k + 41 = 0 дает нам оставшиеся корни k 4 , 5 = 4 ± 5 · i .

Ответ: общим решением заданного ЛОДУ с постоянными коэффициентами будет: y 0 = e 2 x · C 1 + C 2 x + C 3 · e — 3 x + e 4 x · C 4 · cos 5 x + C 5 · sin 5 x

Таким образом, мы рассмотрели основные случаи, когда возможно определить y 0 — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами.

Следующее, что мы разберем – это ответ на вопрос, как решить линейное неоднородное дифференциальное уравнение n -ого порядка с постоянными коэффициентами записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) .

Общее решение в таком случае составляется как сумма общего решения соответствующего ЛОДУ и частного решения исходного ЛНДУ: y = y 0 + y

. Поскольку мы уже умеем определять y 0 , остается разобраться с нахождением y

, т.е. частного решения ЛНДУ порядка n с постоянными коэффициентами.

Приведем все способы нахождения y

согласно тому, какой вид имеет функция f ( x ) , находящаяся в правой части рассматриваемого ЛНДУ.

Когда f ( x ) представлена в виде многочлена n -ой степени f ( x ) = P n ( x ) , частным решением ЛНДУ станет: y

= Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом степени n , а r – указывает, сколько корней характеристического уравнения равно нулю.
Когда функция f ( x ) представлена в виде произведения многочлена степени n и экспоненты f ( x ) = P n ( x ) · e α · x , частным решением ЛНДУ второго порядка станет: y

= e α · x · Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом n —ой степени, r указывает, сколько корней характеристического уравнения равно α .
Когда функция f ( x ) записана как f ( x ) = A 1 cos ( β x ) + B 1 sin ( β x ) , где А 1 и В 1 – числа, частным решением ЛНДУ станет запись y

= A cos β x + B sin β x · x γ . Здесь где А и В являются неопределенными коэффициентами, r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно ± i β .
Когда f ( x ) = e α x · P n ( x ) sin β x + Q k x cos β x , то y

= e α x · L m x sin β x + N m x cos β x · x γ , где r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно α ± i β , P n ( x ) , Q k ( x ) , L m ( x ) и N m ( x ) являются многочленами степени n , k , m и m соответственно, m = m a x ( n , k ) .

Коэффициенты, которые неизвестны, определяются из равенства y

( n — 1 ) + . . . + f 1 y

Подробности нахождения решений уравнений в каждом из указанных случаев можно изучить в статье линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, поскольку схемы решения ЛНДУ степени выше второй полностью совпадают.

Когда функция f ( x ) имеет любой иной вид, общее решение ЛНДУ возможно определить, используя метод вариации произвольных постоянных. Его разберем подробнее.

Пусть нам заданы y j , j = 1 , 2 , . . . , n — n линейно независимые частные решения соответствующего ЛОДУ, тогда, используя различные вариации произвольных постоянных, общим решением ЛНДУ
n -ого порядка с постоянными коэффициентами будет запись: н = ∑ j = 1 n C j ( x ) · y j . В нахождении производных функций C j ( x ) , j = 1 , 2 , . . . , n поможет система уравнений:

∑ j = 1 n C j ‘ ( x ) · y j = 0 ∑ j = 1 n C j ‘ ( x ) · y ‘ j = 0 ∑ j = 1 n C j ‘ ( x ) · y » j = 0 … ∑ j = 1 n C j ‘ ( x ) · y j ( n — 2 ) = 0 ∑ j = 1 n C j ‘ ( x ) · y j ( n — 1 ) = 0

а собственно функции C j ( x ) , j = 1 , 2 , . . . , n найдем при последующем интегрировании.

Задано ЛНДУ с постоянными коэффициентами: y ‘ ‘ ‘ — 5 y » + 6 y ‘ = 2 x . Необходимо найти его общее решение.

Решение

Составим характеристическое уравнение: k 3 — 5 k 2 + 6 k = 0 . Корни данного уравнения: k 1 = 0 , k 2 = 2 и k 3 = 3 . Таким образом, общим решением ЛОДУ будет запись: y 0 = C 1 + C 2 · e 2 x + C 3 · e 3 x , а частные линейно независимые решения это: y 1 = 1 , y 2 = e 2 x , y 3 = e 3 x .

Варьируем произвольные постоянные: y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x .

Чтобы определить C 1 ( x ) , C 2 ( x ) и C 3 ( x ) , составим систему уравнений:

C ‘ 1 ( x ) · y 1 + C ‘ 2 ( x ) · y 2 + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · y ‘ 1 + C ‘ 2 ( x ) · y ‘ 2 + C ‘ 3 ( x ) · y ‘ 3 = 0 C ‘ 1 ( x ) · y » 1 + C ‘ 2 ( x ) · y » 2 + C ‘ 3 ( x ) · y » 3 = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · 1 ‘ + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · e 3 x ‘ = 0 C ‘ 1 ( x ) · 1 ‘ ‘ + C ‘ 2 x · e 2 x ‘ ‘ + C ‘ 3 ( x ) · e 3 x ‘ ‘ = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x + C ‘ 3 ( x ) · e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 2 e 2 x + C ‘ 3 ( x ) · 3 e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 4 e 2 x + C ‘ 3 ( x ) · 9 e 3 x = 2 x

Решаем, используя метод Крамера:

∆ = 1 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 0 4 e 2 x 9 e 3 x = 18 e 2 x · e 3 x — 12 e 2 x · e 3 x = 6 e 5 x ∆ C 1 ‘ ( x ) = 0 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 2 x 4 e 2 x 9 e 3 x = e 5 x · 2 x ⇒ C ‘ 1 ( x ) = ∆ C 1 ‘ ( x ) ∆ = e 5 x · 2 x 6 e 5 x = 1 6 · 2 x ∆ C 2 ‘ ( x ) = 1 0 e 3 x 0 0 3 e 3 x 0 2 x 9 e 3 x = — 3 e x · 2 x ⇒ C ‘ 2 ( x ) = ∆ C 2 ‘ ( x ) ∆ = — 3 e 3 x · 2 x 6 e 5 x = — 1 2 · e — 2 x · 2 x ∆ C 3 ‘ ( x ) = 1 e 2 x 0 0 2 e 2 x 0 0 4 e 2 x 2 x = 2 e 2 x · 2 x ⇒ C ‘ 3 ( x ) = ∆ C 3 ‘ ( x ) ∆ = 2 e 2 x · 2 x 6 e 5 x = 1 3 · e — 3 x · 2 x

Интегрируем C ‘ 1 ( x ) = 1 6 · 2 x с помощью таблицы первообразных, а
C ‘ 2 ( x ) = — 1 2 · e — 2 x · 2 x и C ‘ 3 ( x ) = 1 3 · e — 3 x · 2 x при помощи метода интегрирования по частям, получим:
C 1 ( x ) = 1 6 · ∫ 2 x d x = 1 6 · 2 x ln 2 + C 4 C 2 ( x ) = — 1 2 · ∫ e — 2 x · 2 x d x = — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 C 3 ( x ) = 1 3 · ∫ e — 3 x · 2 x d x = 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6

Ответ: искомым общим решением заданного ЛОДУ с постоянными коэффициентами будет:

y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x = = 1 6 · 2 x ln 2 + C 4 + — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 · e 2 x + + 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6 · e 3 x

где C 4 , C 5 и C 6 – произвольные постоянные.