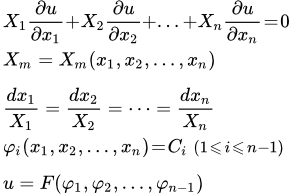Линейные дифференциальные уравнения в частных производных первого порядка
Линейные однородные уравнения в частных производных первого порядка
Пусть X 1 , X 2 , . Xn – заданные функции переменных x 1 , x 2 , . xn .
Чтобы решить линейное однородное уравнение в частных производных первого порядка:
необходимо решить систему обыкновенных дифференциальных уравнений (уравнение характеристик):
:
Далее нужно представить решение в виде:
φ 1( x 1 , x 2 , . xn ) = C 1 ,
φ 2( x 1 , x 2 , . xn ) = C 2 ,
.
φn- 1 ( x 1 , x 2 , . xn ) = Cn- 1 ,
где Ck – постоянные.
После чего сразу получаем общее решение:
,
где F – произвольная функция от n – 1 аргументов.
Если нужно получить частное решение с определенными граничными условиями, то необходимо подставить значения переменных из граничных условий в общее решение и найти вид функции F .
Линейные неоднородные уравнения в частных производных первого порядка
Пусть X 1 , X 2 , . Xn+ 1 – заданные функции от переменных x 1 , x 2 , . xn и z .
Чтобы решить линейное неоднородное уравнение в частных производных первого порядка:
,
необходимо решить уравнение характеристик:
.
Решение этой системы нужно представить в следующем виде:
φ 1( x 1 , x 2 , . xn , z ) = C 1 ,
φ 2( x 1 , x 2 , . xn , z ) = C 2 ,
.
φn ( x 1 , x 2 , . xn , z ) = Cn .
После чего сразу получаем общий интеграл в неявном виде:
где F – произвольная функция. Также общий интеграл можно представить в различных вариантах, например:
φ 1 = F ( φ 2 , φ 3 , . φn ) ,
φ 2 = F ( φ 1 , φ 3 , . φn ) ,
и т. д.
Примеры решений линейных уравнений в частных производных первого порядка
Однородное уравнение
Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .
Это линейное однородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:
Это уравнение характеристик содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье будет выполнено автоматически.
Выбираем и решаем первое уравнение:
Здесь переменные уже разделены, интегрируем:
Интегралы табличные,
Потенцируем:
Отсюда
Подставим во второе уравнение:
Или:
Это линейное уравнение. Решаем с помощью интегрирующего множителя. Умножим на x -1 и преобразуем:
Интегрируем:
Подставим полученное ранее выражение C1 = x y 2 :
Итак, мы нашли два интеграла уравнения характеристик:
Общее решение исходного уравнения в частных производных имеет вид:
где F — произвольная функция от двух аргументов F(φ1, φ2) . Найдем ее вид из граничного условия
при .
Рассматриваем решение на границе.
Положим x y = –1 :
Отсюда
На границе
.
Итак, мы нашли, что на границе функция F имеет вид:
F ( φ 1 , φ 2 ) = φ 1 φ 2 .
Такой же вид она имеет и во всей области
Подставляя
;
,
получаем частное решение исходного уравнения в частных производных с заданным граничным условием:
Общее решение:
где F — произвольная функция от двух аргументов F ( φ 1 , φ 2 ) .
Неоднородное уравнение
Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность x + y + z = 0 , x 2 + y 2 + z 2 = a 2 .
Это линейное неоднородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:
Оно содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье удовлетворится автоматически. Выбираем первое и второе уравнения.
Решаем уравнение:
Умножаем на 2 z и интегрируем:
Интегралы табличные,
Потенцируем:
Отсюда
x = C 1 y
Подставим во второе уравнение:
Или:
Замечаем, что , тогда
Это линейное уравнение. Решаем с помощью интегрирующего множителя. Разделим на y 2 и преобразуем:
Интегрируем:
Подставим полученное ранее выражение и преобразуем:
Итак, мы нашли два интеграла уравнения характеристик:
Для удобства дальнейших вычислений заметим, что функция от постоянной также является постоянной. Поэтому запишем интегралы в виде:
Общий интеграл исходного уравнения в частных производных имеет вид:
F ( φ 1 , φ 2) = 0
Но, поскольку F — произвольная функция от двух аргументов, то общий интеграл можно записать также в виде:
φ 1 = F ( φ 2) ,
где F — произвольная функция от одного аргумента.
Найдем вид этой функции, рассматривая решение на границе.
На границе, x 2 + y 2 + z 2 = a 2 , .
Из уравнения x + y + z = 0 , z = – ( x + y ) . Подставим в x 2 + y 2 + z 2 = a 2 и преобразуем:
x 2 + y 2 + ( x + y ) 2 = a 2
x 2 + y 2 + x 2 + 2 xy + y 2 = a 2
2 x 2 + 2 xy + 2 y 2 = a 2
Разделив на y 2 , имеем
Итак, мы нашли, что на границе:
.
Подставим в выражение общего интеграла:
φ 1 = F ( φ 2)
.
Сделаем подстановку
:
.
Итак, мы нашли, что на границе функция F имеет вид:
.
Такой же вид она имеет и во всей области, тогда
.
Подставляем выражения для φ1 и φ2 :
.
Умножим на a 2 y 2 .
Автор: Олег Одинцов . Опубликовано: 23-09-2014
Реферат: Использование дифференциальных уравнений в частных производных для моделирования реальных процес
| Название: Использование дифференциальных уравнений в частных производных для моделирования реальных процес Раздел: Рефераты по математике Тип: реферат Добавлен 10:52:30 29 августа 2006 Похожие работы Просмотров: 961 Комментариев: 23 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать | |||||||||||||
|
Выполнила: студентка 5-го курса
дневной формы обучения
Прокофьевой Я. К.
Студенческий билет № 95035
|
Научный руководитель:доцент, канд.
Глава 1. Уравнения гиперболического типа.
§1.1. Задачи, приводящие к уравнениям гиперболического типа..………………5
1.1.2. Уравнение электрических колебаний в проводах…….………………8
§1.2. Метод разделения переменных ……………………………………………..10
1.2.1. Уравнение свободных колебаний струны….…………………………10
Глава 2. Уравнения параболического типа.
§2.1. Задачи, приводящие к уравнениям параболического типа………………..17
2.1.1. Уравнение распространения тепла в стержне.……………………….17
2.1.2. Распространение тепла в пространстве.………………………………19
Глава 3. Моделирование с помощью дифференциальных уравнений в частных производных.
§3.1. Дифракция излучения на сферической частице……………………………29
Изучением дифференциальных уравнений в частных производных занимается математическая физика. Основы теории этих уравнений впервые были изложены в знаменитом «Интегральном исчислении» Л. Эйлера.
Классические уравнения математической физики являются линейными. Особенность линейных уравнений состоит в том, что если U и V – два решения, то функция aU + bV при любых постоянных a и b снова является решением. Это обстоятельство позволяет построить общее решение линейного дифференциального уравнения из фиксированного набора его элементарных решений и упрощает теорию этих уравнений.
Современная общая теория дифференциальных уравнений занимается главным образом линейными уравнениями и специальными классами нелинейных уравнений. Основным методом решения нелинейных дифференциальных уравнений в частных производных выступает численное интегрирование.
Круг вопросов математической физики тесно связан с изучением различных физических процессов. Сюда относятся явления, изучаемые в гидродинамике, теории упругости, электродинамике и т.д. Возникающие при этом математические задачи содержат много общих элементов и составляют предмет математической физики.
Постановка задач математической физики, будучи тесно связанной с изучением физических проблем, имеет свои специфические черты. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов.
Круг вопросов, относящихся к математической физике, чрезвычайно широк. В данной работе рассматриваются задачи математической физики, приводящие к уравнениям с частными производными.
Расположение материала соответствует основным типам уравнений. Изучение каждого типа уравнений начинается с простейших физических задач, приводящих к уравнениям рассматриваемого типа.
Глава 1. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
§1.1. Задачи, приводящие к уравнениям гиперболического типа.
Уравнения с частными производными 2-го порядка гиперболического типа наиболее часто встречаются в физических задачах, связанных с процессами колебаний. Простейшее уравнение гиперболического типа
называется волновым уравнением. К исследованию этого уравнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т.д.
1.1.1. Уравнение колебаний струны.
В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени, направлены по касательной к ее профилю. Пусть струна длины 
в начальный момент направлена по отрезку оси Оx от 0 до . Предположим, что концы струны закреплены в точках 
. Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя струны, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения – говорят, что струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.
Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси Ox и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией 
, которая дает величину перемещения точки струны с абсциссой x в момент t.
 |
Так как мы рассматриваем малые отклонения струны в плоскости 
, то будем предполагать, что длина элемента струны 
равняется ее проекции на ось Ox, т.е. 
.1 Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.
Рассмотрим элемент струны 
.
 | |
|
На концах этого элемента, по касательным к струне, действуют силы Т. Пусть касательные образуют с осью Ox углы 
. Тогда проекция на ось Ou сил, действующих на элемент , будет равна 
. Так как угол 
мал, то можно положить 
, и мы будем иметь:
(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).
Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть 
— линейная плотность струны. Тогда масса элемента струны будет 
. Ускорение элемента равно 
. Следовательно, по принципу Даламбера будем иметь:
.
Сокращая на 
и обозначая 
, получаем уравнение движения
. (1)
Это и есть волновое уравнение – уравнение колебаний струны. Для полного определения движения струны одного уравнения (1) недостаточно. Искомая функция 
должна удовлетворять еще граничным условиям, указывающим, что делается на концах струны 
, и начальным условиям, описывающим состояние струны в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.
Пусть, например, как мы предполагали, концы струны при неподвижны. Тогда при любом t должны выполнятся равенства:
(2’)
(2’’)
Эти равенства являются граничными условиями для нашей задачи.
В начальный момент t = 0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f (x). Таким образом, должно быть
(3’)
Далее, в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией 
. Таким образом, должно быть
(3’’)
Условия (3’) и (3’’) являются начальными условиями.
Замечание. В частности, может быть 
или 
. Если же и , то струна будет находится в покое, следовательно, 
.
1.1.2. Уравнение электрических колебаний в проводах.
Как указывалось выше, к уравнению (1) приводит и задача об электрических колебаниях в проводах. Электрический ток в проводе характеризуется величиной i (x, t) и напряжением v (x, t), которые зависят от координаты x точки провода и от времени t. Рассматривая элемент провода , можем написать, что падение напряжения на элементе равно 
. Это падение напряжения складывается из омического, равного 
, и индуктивного, равного 
. Итак,
(4)
где R и L – сопротивление и коэффициент индуктивности, рассчитанные на единицу длины провода. Знак минус взят потому, что ток течет в направлении, обратном возрастанию v. Сокращая на , получаем уравнение
(5)
Далее, разность токов, выходящего из элемента и входящего в него за время 
, будет
Она расходуется на зарядку элемента, равную 
, и на утечку через боковую поверхность провода вследствие несовершенства изоляции, равную 
(здесь А – коэффициент утечки). Приравнивая эти выражения и сокращая на 
, получим уравнение
(6)
Уравнения (5) и (6)принято называть телеграфными уравнениями.
Из системы уравнений (5) и (6) можно получить уравнение, содержащее только искомую функцию i (x, t), и уравнение, содержащее только искомую функцию v (x, t). Продифференцируем члены уравнения (6) по x; члены уравнения (5) продифференцируем по t и умножим их на С. Произведя вычитание, получим:
Подставляя в последнее уравнение выражение 
из уравнения (5), получим:
(7)
Аналогичным образом получается уравнение для определения v (x, t):
(8)
Если пренебречь утечкой через изоляцию 
и сопротивлением 
, то уравнения (7) и (8) переходят в волновые уравнения:
где обозначено: 
. Исходя из физических условий, формулируют граничные и начальные условия задачи.
§1.2. Метод разделения переменных.
1.2.1. Уравнение свободных колебаний струны.
Метод разделения переменных или метод Фурье, является одним из наиболее распространенных методов решения уравнений с частными производными. Изложение этого метода мы проведем для задачи о колебаниях струны, закрепленной на концах. Итак, будем искать решение уравнения
удовлетворяющее однородным граничным условиям
(9)
и начальным условиям
(10)
Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений, можно попытаться при помощи суммирования их с некоторыми коэффициентами найти искомое решение.
Поставим основную вспомогательную задачу: найти решение уравнения
не равное тождественно нулю, удовлетворяющее однородным граничным условиям
(11)
и представимое в виде произведения
(12)
Подставляя предполагаемую форму решения (12) в уравнение (1), получим:
или, после деления на XT,
(13)
Чтобы функция (12) была решением уравнения (1), равенство (13) должно удовлетворяться тождественно, т. е. 0 ‹ х ‹ , t › 0. Правая часть равенства (13) является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства (13) при изменении своих аргументов сохраняют постоянное значение
(14)
где 
– постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.
Из соотношения (14) получаем обыкновенные дифференциальные уравнения для определения функций X (x) и T (t)
(15)
(16)
Граничные условия (11) дают:
Отсюда следует, что функция X (x) должна удовлетворять дополнительным условиям:
X(0) = X() = 0, (17)
Так как иначе мы имели бы
в то время как задача состоит в нахождении нетривиального решения. Для функции T (t) в основной вспомогательной задаче никаких дополнительных условий нет.
Таким образом, в связи с нахождением функции X (x) мы приходим к простейшей задаче о собственных значениях:
найти те значения параметра 
, при которых существуют нетривиальные решения задачи:
(18)
а также найти эти решения. Такие значения параметра называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (18). Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.
Рассмотрим отдельно случаи, когда параметр отрицателен, равен нулю или положителен.
1. При ‹ 0 задача не имеет нетривиальных решений. Действительно, общее решение уравнения (15) имеет вид
Граничные условия дают:
Но в рассматриваемом случае 
– действительно и положительно, так что 
. Поэтому
Х (х)
0.
2. При = 0 также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид
Граничные условия дают:
т. е. С1 = 0 и С2 = 0 и, следовательно,
Х (х)0.
3. При › 0 общее решение уравнения может быть записано в виде
Граничные условия дают:
Если Х(х) не равно тождественно нулю, то D2 
0, поэтому
(19)
где n- любое целое число. Следовательно, нетривиальные решения задачи (18) возможны лишь при значениях
Этим собственным значениям соответствуют собственные функции
где Dn – произвольная постоянная.
Итак, только при значениях , равных
(20)
существуют нетривиальные решения задачи (11)
(21)
определяемые с точностью до произвольного множителя, который мы положили равным единице. Этим же значениям n соответствуют решения уравнения (9)
(22)
где An и Bn – произвольные постоянные.
Возвращаясь к задаче (1), (9), (10), заключаем, что функции
(23)
являются частными решениями уравнения (1), удовлетворяющими граничным условиям (11) и представимыми в виде произведения (12) двух функций, одна из которых зависит только от х, другая – от t. Эти решения могут удовлетворить начальным условиям (10) нашей исходной задачи только для частных случаев начальных функций j(x) и y(x).
Обратимся к решению задачи (1), (9), (10) в общем случае. В силу линейности и однородности уравнения (1) сумма частных решений
(24)
также удовлетворяет этому уравнению и граничным условиям (9). Начальные условия позволяют определить An и Bn . Потребуем, чтобы функция (24) удовлетворяла условиям (10)
(25)
Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция f(x), заданная в промежутке 
, разлагается в ряд Фурье
(26)
(27)
Если функции j(x) и y(x) удовлетворяют условиям разложения в ряд Фурье, то
(28)
(29)
Сравнение этих рядов с формулами (25) показывает, что для выполнения начальных условий надо положить
(30)
чем полностью определяется функция (24), дающая решение исследуемой задачи.
Итак, мы доказали, что ряд (24), где коэффициенты An и Bn определены по формуле (30), если он допускает двукратное почленное дифференцирование, представляет функцию u (x, t), которая является решением уравнения (1) и удовлетворяет граничным и начальным условиям (9) и (10).
Замечание. Решая рассмотренную задачу для волнового уравнения другим методом, можно доказать, что ряд (24) представляет решение и в том случае, когда он не допускает почленного дифференцирования. При этом функция 
должна быть дважды дифференцируемой, а 
— один раз дифференцируемой.
Глава 2. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
§2.1. Задачи, приводящие к уравнениям гиперболического типа.
2.1.1. Уравнение распространения тепла в стержне.
Рассмотрим однородный стержень длины . Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.
Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, а другой – с точкой х = .
 |
Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой
(1)
где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.
Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х1 и х2 (х2 – х1 = 
х). Количество тепла, прошедшего через сечение с абсциссой х1 за время t, будет равно
(2)
то же самое с абсциссой х2 :
(3)
Приток Q1 — Q2 в элемент стержня за время t будет равняться:
(4)
Этот приток тепла за время t затратился на повышение температуры элемента стержня на величину u:
(5)
где с – теплоемкость вещества стержня, – плотность вещества стержня (xS – масса элемента стержня).
Приравнивая выражения (4) и (5) одного и того же количества тепла 
, получим:
|
Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.
Чтобы решение уравнения (6) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (6) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для 
, следующие:
u (, t) = ψ2 (t). (9)
Физическое условие (7) (начальное условие) соответствует тому, что при 
в разных сечениях стержня задана температура, равная φ(x). Условия (8) и (9) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х = поддерживается температура, равная ψ1 (t) и ψ2 (t) соответственно.
Доказывается, что уравнение (6) имеет единственное решение в области 
, удовлетворяющее условиям (7) – (9).
2.1.2. Распространение тепла в пространстве.
Рассмотрим процесс распространения тепла в трехмерном пространстве. Пусть u (x, y, z, t) – температура в точке с координатами (x, y, z) с момент времени t. Опытным путем установлено, что скорость прохождения тепла через площадку 
s, т. е. количество тепла, протекающего за единицу времени, определяется формулой (аналогично формуле (1))
(10)
где k – коэффициент теплопроводности рассматриваемой среды, которую мы считаем однородной и изотропной, n – единичный вектор, направленный по нормали к площадке s в направлении движения тепла. Таким образом, можем записать:
где 
– направляющие косинусы вектора n, или
Подставляя выражение 
в формулу (10), получаем:
Q = -k n grad u s.
Количество тепла, протекающего за время ∆t через площадку ∆s, будет равно:
Qt = -k n grad u t s.
Вернемся к поставленной задаче. В рассматриваемой среде выделим малый объем V, ограниченный поверхностью S. Количество тепла, протекающего через поверхность S, будет равно:
(11)
где n – единичный вектор, направленный по внешней нормали к поверхности S. Очевидно, что формула (11) дает количество тепла, поступающего в объем V (или уходящего из объема V) за время t. Количество тепла, поступившего в объем V, идет на повышение температуры вещества этого объема.
Рассмотрим элементарный объем υ. Пусть за время t его температура поднялась на u. Очевидно, что количество тепла, затраченное на это повышение температуры элемента υ, будет равно
где с – теплоемкость вещества, ρ – плотность. Общее количество тепла, затраченное на повышение температуры в объеме V за время t, будет
Но это есть тепло, поступающее в объем V за время t; оно определено формулой (11) . Таким образом, имеет место равенство
Сокращая на t, получаем:
(12)
Поверхностный интеграл, стоящий в левой части этого равенства, преобразуем по формуле Остроградского (в векторной форме, где F – дивергенция векторного поля, 
– замкнутая поверхность)
полагая F = k grad u:
Заменяя двойной интеграл, стоящий в левой части равенства (12), тройным интегралом, получим:
|
Применив теорему о среднем к тройному интегралу, стоящего слева, получим :
(14)
где P (x, y, z) – некоторая точка объема V.
Так как мы можем выделить произвольный объем V в трехмерном пространстве, где происходит распространение тепла, и так как мы предполагаем, что подынтегральная функция в равенстве (13) непрерывна, то равенство (14) будет выполняться в каждой точке пространства. Итак,
(15)
Подставляя в уравнение (15), получаем:
(16)
Если k – постоянное, то
и уравнение (15) в этом случае дает:
или, положив 
(17)
Коротко уравнение (17) записывается так:
где u – оператор Лапласа. Уравнение (17) и есть уравнение теплопроводности в пространстве. Для того чтобы найти единственное решение, отвечающее поставленной задаче, нужно задать краевые условия.
Пусть имеем тело 
, поверхность которого . В этом теле рассматривается процесс распространения тепла. В начальный момент температура тела задана. Это соответствует тому, что известно значение решения при t = 0 – начальное условие:
u (x, y, z, 0) = φ (x, y, z). (18)
Кроме того, должна быть известна температура в любой точке М поверхности тела в любой момент времени t – граничное условие:
u (М, t) = ψ (М, t). (19)
(Возможны и другие граничные условия.)
Если искомая функция u (x, y, z, t) не зависит от z, что соответствует тому, что температура не зависит от z, то получаем уравнение:
(20)
— уравнение распространения тепла на плоскости. Если рассматривается распространения тепла в плоской области D с границей С, то граничные условия, аналогично (18) и (19), формулируются так:
где φ и ψ – заданные функции, М – точка границы С.
Если же функция u не зависит ни от z, ни от y, то получаем уравнение
— уравнение распространения тепла в стержне.
§2.2. Температурные волны.
Задача о распространении температурных волн в почве является одним из первых примеров приложения математической теории теплопроводности, развитой Фурье, к изучению явлений природы.
Температура на поверхности земли носит, как известно, ярко выраженную суточную и годовую периодичность. Обратимся к задаче о распространении периодических температурных колебаний в почве, которую будем рассматривать как однородное полупространство 
. Эта задача является характерной задачей без начальных условий, так как при многократном повторении температурного хода на поверхности влияние начальной температуры будет меньше влияния других факторов, которыми мы пренебрегаем (например, неоднородность почвы). Таким образом, приходим к следующей задаче:
найти ограниченное решение уравнения теплопроводности
(1)
u (0, t) = A cos 
t. (2)
Предполагается, что функции u (x, t) и m (t) ограничены всюду, т.е.
Запишем граничное условие в виде
(2’)
Из линейности уравнения теплопроводности следует, что действительная и мнимая части некоторого комплексного решения уравнения теплопроводности каждая в отдельности удовлетворяет тому же решению.
Если найдено решение уравнения теплопроводности, удовлетворяющее условию (2’), то его действительная часть удовлетворяет условию (2), а мнимая – условию
Итак, рассмотрим задачу:
(3)
Ее решение будем искать в виде
(4)
где 
и 
— неопределенные пока постоянные.
Подставляя выражение (4) в уравнение (3) и граничное условие, находим:
,
Для u (x, t) имеем:
(5)
Действительная часть этого решения
(6)
удовлетворяет уравнению теплопроводности и граничному условию (2). Формула (6) в зависимости от выбора знака определяет не одну, а две функции. Однако только функция, соответствующая знаку минус, удовлетворяет требованию ограниченности. Таким образом, решение поставленной задачи получаем в виде
(7)
На основании полученного решения можно дать следующую характеристику процесса распространения температурной волны в почве. Если температура поверхности длительное время периодически меняется, то в почве также устанавливаются колебания температуры с тем же периодом, причем:
1.Амплитуда колебаний экспоненционально убывает с глубиной
,
т.е. если глубины растут в арифметической прогрессии, то амплитуды убывают в геометрической прогрессии (первый закон Фурье).
2. Температурные колебания в почве происходят со сдвигом фазы. Время 
запаздывания максимумов (минимумов) температуры в почве от соответствующих моментов на поверхности пропорционально глубине
(второй закон Фурье).
3. Глубина проникновения тепла в почву зависит от периода колебаний температуры на поверхности. Относительное изменение температурной амплитуды равно
Эта формула показывает, что чем меньше период, тем меньше глубина проникновения температуры. Для температурных колебаний с периодами Т1 и Т2 глубины x1 и x2 , на которых происходит одинаковое относительное изменение температуры, связаны соотношением
(третий закон Фурье). Так, например, сравнение суточных и годовых колебаний, для которых Т2 = 365 Т1 , показывает, что
т.е. что глубина проникновения годовых колебаний при одинаковой амплитуде на поверхности была бы в 19,1 раза больше глубины проникновения суточных колебаний.
Следует, однако, иметь в виду, что изложенная здесь теория относится к распространению тепла в сухой почве или горных породах. Наличие влаги усложняет температурные явления в почве, при замерзании происходит выделение скрытой теплоты, не учитываемое этой теорией.
Температуропроводность является одной из характеристик тела, важных для изучения его физических свойств, а также для различных технических расчетов. На изучении распространения температурных волн в стержнях основан один из лабораторных методов определения температуропроводности.
Пусть на конце достаточно длинного стержня поддерживается периодическая температура 
(t). Представив эту функцию в виде ряда Фурье
где Т – период, и взяв температурные волны, соответствующие каждому слагаемому, получим, что температура u (x, t) для любого x будет периодической функцией времени и ее n-я гармоника равна
Эта формула показывает, что если произвести измерение температуры в каких-нибудь двух точках, x1 и x2 , за полный период, то, находя коэффициенты an (x1 ), bn (x1 ), an (x2 ), bn (x2 ) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а 2 .
Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ.
§3.1. Дифракция излучения на сферической частице.
Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в случае монохроматического излучения частоты система уравнений Максвелла сводится к системе уравнений для напряженностей электрического 
и магнитного 
полей:
(1)
где 
— волновое число для пустоты; с0 – скорость света в вакууме. Обозначим через k = k0 m – волновое число в среде с комплексным показателем преломления m = n – ix. Показатели преломления и поглощения (n и x) называются оптическими постоянными, их зависимость от w обычно известна из эксперимента.
Задача о разыскании шести неизвестных функций (
) может быть сведена к задаче о разыскании двух функций – электрического и магнитного потенциалов (U1 и U2 ), которые являются решениями колебательного уравнения. Получим их по методу Фурье в виде бесконечных сумм частных решений с неопределенными коэффициентами, которые определяются «сшиванием» значений внутри и снаружи сферы. Через найденные потенциалы составляющие полей легко вычисляются дифференцированием.
Пусть на сферическую частицу радиуса а, центр которой совмещен с началом координат, в отрицательном напрвлении оси Oz падает линейно поляризованная плоская волна (рис 4.). Ось Ox является направлением электрических колебаний, а ось Oy – магнитных. Электрическое и магнитное поля в падающей волне описываются формулами:
(2)
где ka = ma k0 – величина волнового вектора падающего излучения во внешней среде с вещественным показателем преломления ma .
 |
Рис. 3.1. Сферическая система координат для изучения
дифракции света на шаре.
В дальнейшем в промежуточных формулах всюду будет опущен множитель Е0 , который будет внесен в окончательные выражения для полей.
В сферической системе координат, в которой естественно решать данную задачу, уравнения Максвелла (1) имеют вид:
(5)
(6)
(7)
(8)
Падающее поле возбуждает в шаре внутреннее поле, а во внешнем пространстве – дифрагированное поле, причем все эти поля должны иметь оду и ту же временную зависимость, т.е. частоту. Произвольное электромагнитное поле будем представлять как суперпозицию двух типов колебаний. Первый тип назовем электрическими колебаниями и будем считать, что у этих колебаний радиальная составляющая магнитного поля во всех точках равна нулю:
(9)
Второй тип – магнитные колебания:
(10)
В случае электрических колебаний из уравнения (6) получим
Это соотношение, очевидно, будет удовлетворено, если предположим, что 
есть производные от некоторой третьей функции 
: первая – по 
, а вторая – по 
:
Подставляя эти соотношения в формулы (4) и (5) получим
Этим соотношениям можно удовлетворить, если положить 
где 
— некоторая новая функция. Тогда найдем 
. Если теперь вместо функции ввести 
, то формула (3) получит вид
(11)
тогда как (7) и (8) приводятся к одному и тому же волновому уравнению для функции 
Используя указанные выше соотношения и заменяя в выражении для 
производные по 
через производные по r из уравнения (12), получим следующие соотношения:
(13)
которые выражают все составляющие полей для случая 
через одну функцию — потенциал электрических колебаний. Подставив эти выражения в уравнение (3) – (8), легко убедиться в том, что равенства (13) образуют решение уравнений Максвелла, если U1 является решением волнового уравнения. Аналогично для магнитных колебаний все составляющие полей могут быть выражены через некоторую функцию 
— потенциал магнитных колебаний.
В общем случае в поле присутствуют колебания обоих типов. Для составляющих полей получим при этом следующие выражения:
(14)
Функции U1 и U2 являются решением волнового уравнения.
(15)
которое будем решать по методу Фурье (значок у U временно опущен, он появится при рассмотрении граничных условий, которые для U1 и U2 различны). В качестве частного решения положим
(16)
Подставляя (16) в (13) и разделяя переменные, получим для f и Y следующие уравнения:
(17)
(18)
Уравнение для Y имеет однозначное и непрерывное решение на всей сфере только для 
, где n = 0, 1, 2… В этом случае его решением являются сферические функции:
(19)
где 
а 
— полином Лежандра. В уравнении (17) сделаем подстановку 
, тогда для Rn (x) получим следующее уравнение (x = kr):
(20)
Это уравнение Бесселя и его решением являются цилиндрические функции с полуцелым индексом 
. Таким образом, n-е частное решение уравнения (15) будет
(21)
Из всех цилиндрических функций только бесселевы функции первого рода 
конечны в нуле. Поэтому только они могут быть использованы для решения внутри шара. Вне шара, в соответствии с принципом излучения, решение должно иметь характер расходящейся волны. Так как временной множитель выбран в виде 
, то только ханкелевская функция второго рода 
дает волну, расходящуюся из источника дифракции 
. Обозначим
(22)
тогда частное решение, очевидно, следует представить в виде суперпозиции частных решений с неопределенными коэффициентами, которые вычисляются из граничных условий. Граничные условия для потенциалов U1 и U2 на шаре получаются из требования непрерывности тангенциальных () составляющих полей. Из (14) видно, что для этого необходимо, чтобы на поверхности шара были непрерывны следующие величины: 
, т.е.
(23)
(24)
где U a – потенциал дифрагированного поля, а U i – внутреннего.
Представим теперь электрический и магнитный потенциалы падающей волны также в виде рядов по 
, используя известное разложение плоской волны по полиномам Лежандра:
(25)
Тогда после преобразований получим:
(26)
Потенциалы 
и 
должны иметь такую же угловую зависимость, как и потенциалы падающего поля. Поэтому можно записать:
(27)
(28)
Коэффициенты 
должны быть определены из условий (23), (24), которые образуют относительно пар коэффициентов 
и 
с данным значком 
две независимые системы по два линейных уравнения. Запишем их, введя следующие обозначения: 
; 
— относительный (комплексный) показатель преломления, 
— длина волны излучения. Для 
и 
имеем:
(29)
Аналогичная система получается для 
и 
:
(30)
Решая эти системы относительно и , получим:
(31)
Аналогичные выражения получаются и для и . Подставляя эти выражения в (27) и (28), получаем однозначное решение уравнений для потенциалов, удовлетворяющее всем граничным условиям. Из потенциалов, в соответствии с (14), можно получить выражения для составляющих внутреннего и дифрагированного полей. Так как в дальнейшем нас будет интересовать дифрагированное поле, то выпишем только его составляющие, восстановив опущенный ранее множитель Е0 :
(32)
Штрихи всюду означают производные по аргументу, указанному под знаком функции ( 
и 
). На достаточно большом расстоянии от рассматриваемой частицы, в так называемой волновой зоне, можно пренебречь составляющими Er и Hr по сравнению с составляющими по и 
. Дифрагированное поле будет являться поперечной волной, распространяющейся из источника дифракции. Введя обозначения
(33)
(34)
и применяя асимптоматические выражения для функций 
при 
, получим:
(35)
Согласно этим формулам, дифрагированное поле представляется в виде сумм отдельных парциальных волн. Интенсивность возбуждения 
-й парциальной волны определяется числами 
, которые существенно зависят от 
.
Поле вне частицы 
есть суперпозиция падающего 
и дифрагированного 
полей:
(36)
Средняя по времени величина вектора потока энергии определяется
(37)
где 
— вектор, комплексно сопряженный к 
. В силу (36) поток может быть представлен в виде 
, где 
— поток падающего поля, 
— дифрагированного поля и 
— поток, обязанный интерференции падающего и рассеянного излучений. Определим величины сечений поглощения сп и рассеяния ср излучения частицей
(38)
где J0 – интенсивность падающего излучения, 
— радиальные составляющие потоков, 
— элемент телесного угла, а 
— элемент площади на сфере. Все интегралы распространены по сфере. Полное ослабление потока в результате прохождения им частицы будет складываться из рассеяния и поглощения, т.е. для сечения ослабления излучения частицей имеем с = сп + ср . Поскольку поток падающего излучения постоянен по направлению, то 
и для искомых сечений получим
(39)
(40)
Рассмотрим интеграл в (39). Имеем 
Подставляя сюда выражение (32) для полей, выполняя интегрирование по 
и группируя соответствующим образом члены, получим двойную сумму следующих двух типов выражений:
Сумма будет иметь общий множитель 
. Оба интеграла легко вычисляются. Интеграл а) равен нулю, так как его подынтегральное выражение есть 
, а функция 
равна нулю при 
. В интеграле б) преобразуем вначале первое слагаемое, проинтегрировав его по частям
Заключение
В дипломной работе приведены некоторые примеры применения дифференциальных уравнений для моделирования таких реальных процессов, как колебания струны, электрические колебания в проводах, распространение тепла в стержне и пространстве, распространение температурных волн в почве, дифракция излучения на сферической частице.
Работа начинается с рассмотрения простейших задач, приводящих к дифференциальным уравнениям гиперболического типа (колебания струны, электрические колебания в проводах). Затем рассматривается один из методов решения уравнений данного типа. Во второй главе рассматриваются дифференциальные уравнения параболического типа (распространение тепловых волн) и одно из приложений к данной сфере – температурные волны. В третьей главе рассматривается вывод уравнения дифракции излучения на сферической частице.
Вследствие большого объема теории по применению дифференциальных уравнений для моделирования реальных процессов в данной дипломной работе не мог быть рассмотрен весь материал.
В заключение хотелось бы отметить особую роль дифференциальных уравнений при решении многих задач математики, физики и техники, так как часто не всегда удается установить функциональную зависимость между искомыми и данными переменными величинами, но зато удается вывести дифференциальное уравнение, позволяющее точно предсказать протекание определенного процесса при определенных условиях.
1. Н. С.Пискунов «Дифференциальное и интегральное исчисления», М., «Наука», 1972, том. 2.
2. И. М. Уваренков, М. З. Маллер «Курс математического анализа», М., «Просвещение», 1976.
3. А. Н. Тихонов, А. А. Самарский «Уравнения математической физики», М., «Наука», 1972.
4. Владимиров В. С. «Уравнения математической физики», М., «Наука», 1988.
1 Это предположение эквивалентно тому, что мы пренебрегаем величиной 
по сравнению с 1. Действительно, 
.
Линейные дифференциальные уравнения в частных производных курсовая
. Основы теории дифференциальных уравнений в частных производных
.1 Основные определения теории уравнений в частных производных
.2 Физические задачи, приводящие к уравнениям в частных производных
. Использование вероятностных методов в решении уравнений в частных производных
.1 Общее описание методов Монте-Карло
.2 Решение уравнений в частных производных методом Монте-Карло на примере задачи Дирихле для уравнений Лапласа и Пуассона
Для сложных математических моделей аналитические решения удаётся получить сравнительно редко. Поэтому среди приближённых математических методов основными методами решения задач являются численные. Эти методы позволяют добиться хорошего качественного и количественного описания исследуемого процесса или явления.
Задача Дирихле может быть сформулирована следующим образом: найти функцию, непрерывную в данной замкнутой области , гармоническую в области и принимающую на ее границе непрерывные заданные значения. В рамках данной работы проведено рассмотрение решения задачи Дирихле для уравнения Лапласа и уравнения Пуассона методом Монте-Карло на основе метода сеток.
Применяя метод сеток для решения краевых задач, прежде всего, появляется задача замены дифференциальных уравнений разностными уравнениями — заданное дифференциальное уравнение заменяется в узлах построенной сетки соответствующим конечно-разностным уравнением.
Идея метода сеток восходит еще к Эйлеру [17, c.83]. Однако практическое использование метода наталкивалось на серьезные трудности, так как получение достаточно точного решения краевой задачи приводило к системам алгебраических уравнений, на решение которых при ручном счете требовались затраты времени. Положение резко изменилось с появлением быстродействующих электронных вычислительных машин.
Методами Монте-Карло называются численные методы решения математических задач при помощи моделирования случайных величин и статистической оценки их характеристик. В данной работе приведено два метода решения задачи Дирихле для уравнения Лапласа с использованием методом Монте-Карло, и на основании одного из них приведена программа его реализующая.
Целью данной работы является исследование вероятностных методов решения уравнений в частных производных.
изучение основных положений теории дифференциальных уравнений в частных производных;
классификация уравнений в частных производных;
изучение методов решения уравнений в частных производных;
изучение методов Монте-Карло;
применение метода Монте-Карло для решения задачи Дирихле для уравнений Лапласа и Пуассона.
Объект исследования: дифференциальные уравнения в частных производных.
Предмет исследования: вероятностные методы решения уравнений в частных производных.
Работа состоит из двух глав, введения, заключения и списка литературы. В главе 1 приведены основные понятия теории дифференциальных уравнений в частных производных и показано их практическое применение. В главе 2 приведено описание методов Монте-Карло в контексте задач решения уравнений в частных производных.
1. Основы теории дифференциальных уравнений в частных производных
.1 Основные определения теории уравнений в частных производных
Теория дифференциальных уравнений — раздел математики, который занимается изучением дифференциальных уравнений и связанных с ними задач. Её результаты применяются во многих естественных науках, особенно широко — в физике.
Неформально говоря, дифференциальное уравнение — это уравнение, в котором неизвестной величиной является некоторая функция. При этом в самом уравнении участвует не только неизвестная функция, но и различные производные от неё. Дифференциальным уравнением описывается связь между неизвестной функцией и её производными. Такие связи обнаруживаются в самых разных областях знания: в механике, физике, химии, биологии, экономике и др.
Различают обыкновенные дифференциальные уравнения (ОДУ) и дифференциальные уравнения в частных производных (УРЧП). Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы [18, c.28].
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.
Одно из простейших применений дифференциальных уравнений — решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения. Например, в соответствии со вторым законом Ньютона, ускорение тела пропорционально сумме действующих сил; соответствующее дифференциальное уравнение имеет вид. Зная действующие силы (правая часть), можно решить это уравнение и, учитывая начальные условия (координаты и скорость в начальный момент времени), найти траекторию движения точки [16, c.45].
Пусть — некоторая неизвестная функция и т.д. ее частные производные различного порядка.
связывающие независимые переменные х, у, искомую функцию u(х, у) и ее частные производные различного порядка. Уравнение (1) называют дифференциальным уравнением в частных производных.
Порядок уравнения определяется наивысшим порядком частной производной, входящей в это уравнение.
) — дифференциальное уравнение первого порядка.
) — дифференциальное уравнение второго порядка и т.п.
Решением дифференциального уравнения называется любая функция u(х, у), обращающая его в тождество. Задачи, связанные с решением дифференциального уравнения в частных производных, как правило, более сложные по сравнению с задачами для обыкновенных дифференциальных уравнений [18, c.180].
Мы знаем, что общее решение обыкновенных дифференциальных уравнений n-го порядка зависит от n произвольных постоянных С1, С2, …, Сn. Более сложная ситуация складывается при решении дифференциальных уравнений в частных производных. Например, решением дифференциального уравнения является любая функция т.е. общее решение зависит от бесконечного числа функций, зависящих только от одной переменной
Предмет теории уравнений в частных производных составляет изучение дифференциальных уравнений, описывающих то или иное явление природы, по преимуществу физической. Наш курс будет посвящен по преимуществу уравнениям в частных производных второго порядка.
В связи с этим рассмотрим некоторые физические задачи, приводящие к решению дифференциальных уравнений в частных производных [5, c.58].
Теория дифференциальных уравнений является одним из самых больших разделов современной математики. Чтобы охарактеризовать ее место в современной математической науке, прежде всего, необходимо подчеркнуть основные особенности теории дифференциальных уравнений, состоящей из двух обширных областей математики: теории обыкновенных дифференциальных уравнений и теории уравнений с частными производными.
Первая особенность — это непосредственная связь теории дифференциальных уравнений с приложениями. Характеризуя математику как метод проникновения в тайны природы, можно сказать, что основным путем применения этого метода является формирование и изучение математических моделей реального мира. Изучая какие-либо физические явления, исследователь, прежде всего, создает его математическую идеализацию или, другими словами, математическую модель, то есть, пренебрегая второстепенными характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Очень часто эти законы можно выразить в виде дифференциальных уравнений. Такими оказываются модели различных явлений механики сплошной среды, химических реакций, электрических и магнитных явлений и др [5, c.60].
Исследуя полученные дифференциальные уравнения вместе с дополнительными условиями, которые, как правило, задаются в виде начальных и граничных условий, математик получает сведения о происходящем явлении, иногда может узнать его прошлое и будущее. Изучение математической модели математическими методами позволяет не только получить качественные характеристики физических явлений и рассчитать с заданной степенью точности ход реального процесса, но и дает возможность проникнуть в суть физических явлений, а иногда предсказать и новые физические эффекты. Бывает, что сама природа физического явления подсказывает и подходы, и методы математического исследования. Критерием правильности выбора математической модели является практика, сопоставление данных математического исследования с экспериментальными данными.
Постановка задач для уравнений в частных производных включает определение самого уравнения (или системы нескольких уравнений), а также необходимого количества краевых условий (число и характер задания которых определяется спецификой уравнения). По своему названию уравнения должны содержать частные производные неизвестной функции и (или нескольких функций, если уравнений несколько) по различным аргументам, например пространственной переменной х и времени t. Соответственно, для решения задачи требуется вычислить функцию нескольких переменных, например u 0 и находится в прямолинейном положении равновесия. В момент времени t=0 точкам струны сообщаются некоторые отклонения и скорости [12, c.145].
Поставим задачу об определении малых поперечных колебаний точек струны при t>0, если концы струны:
а) жестко закреплены,
в) двигаются в поперечном направлении по заданным законам.
Сопротивлением среды и силой тяжести пренебрегаем.
Решение. Пусть ось ох совпадает с первоначальным положением струны в положении равновесия
Выделим участок струны от А до В и спроектируем все действующие на этот участок силы на ось u. Согласно принципу Даламбера сумма проекций должна равняться нулю.
так как мы рассматриваем малые колебания и — малой величиной пренебрегаем.
Это значит, что удлинение участка струны не происходит и, следовательно, по закону Гука величина натяжения не зависит ни от времени, ни от х.
Проекция силы натяжения
Пусть — непрерывная линейная плотность внешних сил. Тогда на АВ действует вдоль оси u сила
Для нахождения силы инерции воспользуемся выражением где Тогда
Это и есть уравнение вынужденных колебаний струны.
Если ?=const и то
Кроме того, искомая функция u(х, у) должна удовлетворять начальным условиям:
— начальное положение струны
а) струна закреплена на концах
б) в случае свободных концов должно быть
в) — законы движения концов струны.
Задача 2. Уравнение неразрывности. Задача обтекания.
Рассмотрим движение идеальной жидкости (газа), т.е. жидкости в которой отсутствуют силы вязкости [18, c.196].
Пусть — вектор скорости движения жидкости, -ее плотность, — интенсивность источников. Выделим в жидкости некоторый объем ?, ограниченный поверхностью S. Изменение массы жидкости внутри ? в единицу времени равно
с другой стороны это изменение должно равняться приращению количества Q1 жидкости за счет источников
минус количество Q2, вытекающей через S
где — внешняя нормаль к S, таким образом
В силу произвольности ?
Это и есть уравнение неразрывности движения идеальной жидкости.
Рассмотрим теперь задачу обтекания твердого тела ? с границей S потенциальным потоком несжимаемой однородной жидкости, имеющей заданную скорость на бесконечности при отсутствии источников. В этом случае и Поэтому: при условии
Пусть u -потенциал скоростей, т.е. тогда
Задача 3. О распространении тепла
Вывод уравнения теплопроводности базируется на законе Фурье, согласно которому количество тепла, проходящего за время ?t через малую площадку ?S, лежащую внутри рассматриваемого тела, определяется формулой
где — нормаль к ?S, направленная в сторону передачи тепла, k(x, u) — коэффициент внутренней теплопроводности, u(x, t) — температура тела в точке в момент времени t. Предполагается, что тело изотропно в отношении теплопроводности, т.е. k(x, u) не зависит от направления площадки [18, c.165].
Выделим внутри тела объем ?, ограниченный S. Согласно закону Фурье, количество тепла, втекающее через S за промежуток [t1, t2], равно
Если — плотность тепловых источников, то количество тепла, образованного за их счет в ? за указанный промежуток времени, равно
Общее количество тепла притекающего в ? за время от t1 до t2 можно посчитать и за счет приращения температуры
где и — теплоемкость и плотность вещества. Тогда
В силу произвольности ? и промежутка времени t1, t2, следует равенство
называемое уравнением теплопроводности. Если (не зависит от температуры), то уравнение (5) становится линейным. Если же тело однородно и уравнение (5) примет вид [18, c.196]:
Из физических соображений следует, что для однозначного описания процесса распространения тепла необходимо кроме уравнения, задать начальное распределение температуры
— начальное условие и температурный режим на границе
— граничное условие, (возможны и другие варианты задания граничных условий).
2. Использование вероятностных методов в решении уравнений в частных производных
.1 Общее описание методов Монте-Карло
Далеко не всегда удается найти решение дифференциального уравнения в частных производных аналитическим путем. В случаях, не предполагающих нахождения решения уравнения аналитически, используются численные методы.
В рамках данной работы рассматривается группа численных методов, основанная на математическом аппарате теории вероятностей, называемая методами Монте-Карло.
Общепринятого определения методов Монте-Карло пока нет. Назовем методами Монте-Карло численные методы решения математических задач при помощи моделирования случайных величин и статистической оценки их характеристик. При таком определении приходится к методам Монте-Карло причислить некоторые другие методы, как, например, стохастические приближения или случайный поиск, которые по традиции рассматриваются отдельно. Однако специалисты, занимающиеся этими вопросами, нередко сами называют свои приемы методами Монте-Карло. В то же время в определении подчеркивается что [10, c.58]:
а) речь идет о численных методах (и конкурировать они могут с классическими численными методами, а не с аналитическими методами решения задач);
б) решать методами Монте-Карло можно любые математические задачи (а не только задачи вероятностного происхождения, связанные со случайными величинами).
Официальной датой рождения методов Монте-Карло считают 1949 год, когда появилась статья под заглавием «Метод Монте-Карло». Возникновение метода связывают обычно с именами Дж. Неймана, С. Улама, Н. Метрополиса, а также Г. Кана и Э. Ферми; все они в 40-х годах работали в Лос-Аламосе (США) [10, c.69].
Необходимо сразу же подчеркнуть, что теоретические основы методов Монте-Карло были известны значительно раньше. Более того, фактически такие методы не раз использовались для расчетов в математической статистике. Однако до появления электронных вычислительных машин (ЭВМ) методы Монте-Карло не могли стать универсальными численными методами, ибо моделирование случайных величин вручную — весьма трудоемкий процесс [10, c.89].
Развитию методов Монте-Карло способствовало бурное развитие ЭВМ. Алгоритмы Монте-Карло (как правило, обладающие небольшой связностью) сравнительно легко программируются и позволяют рассчитывать многие задачи, недоступные для классических численных методов. Так как совершенствование ЭВМ продолжается, есть все основания ожидать дальнейшего развития методов Монте-Карло и дальнейшего расширения области их применения.
Важнейший прием построения методов Монте-Карло — сведение задачи к расчету математических ожиданий. Более подробно: для того чтобы приближенно вычислить некоторую скалярную величину а, надо придумать такую случайную величину , что ; тогда, вычислив независимых значений величины , можно считать, что .
Пример. Требуется оценить объем некоторой ограниченной пространственной фигуры .
Выберем параллелепипед , содержащий , объем которого известен. Выберем случайных точек, равномерно распределенных в , и обозначим через количество точек, попавших в . Если велико, то, очевидно, : , откуда получаем оценку .
В этом примере случайная величина равна , если случайная точка попадает в , и равна нулю, если точка попадает в . Нетрудно проверить, что математическое ожидание , а среднее арифметическое
Легко видеть, что существует бесконечно много случайных величин таких, что . Поэтому теория методов Монте-Карло должна дать ответы на два вопроса [7, c.87]:
) как выбрать удобную величину для расчета той или иной задачи;
) как находить значения произвольной случайной величины ?
Изучение этих вопросов и должно составить основное содержание практического курса методов Монте-Карло.
Многие методы основаны на расчете математических ожиданий. Существуют методы случайного поиска (кроме простейшего) и стохастических приближений [10, c.105].
Среди методов Монте-Карло можно выделить методы, в которых полностью воспроизводится модель рассчитываемого процесса. Такие методы иногда называют «физическими», хотя автору представляется более удачным другое название этих методов — имитационные. Имитация естественных процессов широко используется в самых различных областях науки, техники, экономики.
.2 Решение уравнений в частных производных методом Монте-Карло на примере задачи Дирихле для уравнений Лапласа и Пуассона
Определение. Функция , имеющая непрерывные частные второго порядка в области и удовлетворяющая внутри уравнению Лапласа, называется гармонической функцией [15, c.78]:
Простейшим примером гармонической функции двух переменных является функция вида , где (основное решение уравнения Лапласа).
Задача Дирихле в иных терминах может быть сформулирована следующим образом: найти функцию, непрерывную в данной замкнутой области , гармоническую в области и принимающую на ее границе непрерывные заданные значения.
Если , то задача Дирихле удовлетворяет уравнению Пуассона Единственность решения задачи Дирихле и непрерывная запись ее от краевых условий (корректность краевой задачи) вытекают из следующих гармонических функций [14, c.40].
Свойство 1 (принцип максимума). Гармоническая в ограниченной области функция, непрерывная в замкнутой области , не может принимать внутри этой области значений больших, чем максимум ее значений на границе непрерывные заданные значения [14, c.45].
Доказательство. Пусть — максимум значений на границе . Допустим, что функция в некоторой точке внутри принимает значение , причем .
Составим вспомогательную функцию
где — диаметр области . Очевидно, имеем
причем при выполняется неравенство
Следовательно, функция достигает своего наибольшего значения внутри области в некоторой точке , причем в этой точке будут выполнены необходимые условия для максимума функции [13, c.28]:
вытекает, что по крайней мере одна из производных или положительна внутри . Поэтому функция ни в какой конкретной точке области не может иметь максимума, и, следовательно, приходим к противоречию. Таким образом, .
Аналогично доказывается, что , где — наименьшее значение функции на границе .
Следствие. Пусть функция — гармоническая в ограниченной области и непрерывная в замкнутой области . В таком случае справедливо равенство , где на , на .
Замечание. Можно доказать более сильное утверждение, что гармоническая в ограниченной и замкнутой области функция, отличная от константы, не принимает внутри наибольшего и наименьшего значений.
Свойство II (единственность решения задачи Дирихле). Задача Дирихле для замкнутой и ограниченной области может иметь лишь единственное решение, т. е. не существует двух непрерывных гармонических функций в замкнутой ограниченной области , принимающих, на границе одни и те же значения [14, c.202].
Доказательство. Допустим, что две функции и гармонические в области , совпадают всюду на ее границе. Рассмотрим функцию
Очевидно, что на — гармоническая функция, обращающаяся в нуль на границе. По свойству I эта функция не может принимать внутри значений больше или меньше нуля, следовательно, внутри и .
Замечание. Из свойства II не следует, что задача Дирихле для ограниченной замкнутой области имеет решение; это свойство лишь утверждает, что если существует решение задачи Дирихле для области , то оно единственно [14, c.158].
Можно доказать, что если область выпуклая, т. е. вместе с двумя своими точками содержит соединяющий их отрезок, и граница ее действительно имеет решение (теорем Неймана).
Свойство III (корректность задачи Дирихле). Решение задачи Дирихле для замкнутой и ограниченной области непрерывно зависит от граничных данных.
Доказательство. Допустим, что и — решения задачи Дирихле, соответственно принимающее на границе значение и .
Пусть всюду на выполнено неравенство
где — произвольное малое положительное число.
Рассмотрим гармоническую функцию
На границе эта функция принимает значение
Так как на , то по свойству I имеем при , т.е. или .
Таким образом, для задачи Дирихле требование корректности выполнено при .
Пусть на плоскости дана область с кусочно-гладкой границей . В области построим квадратную сетку с шагом :
Мы предполагаем, что сетка состоит из внутренних узлов и граничных узлов первого рода. Граничные узлы сетки образуют ее границу. Грубо говоря, граница представляет собой линейный ряд точек , аппроксимирующий криво-криволинейную границу области с точностью до .
Представим себе частицу , которая совершает равномерное случайное блуждание по узлам сетки (1). А именно, находясь во внутреннем узле сетки , эта частица за один переход с одной и той же вероятностью, равной 1/4, может переместиться в один из четырех соседних узлов: или в (шаг влево), или в (шаг вправо), или в (шаг вниз), или в (шаг вверх), причем каждый такой единичный переход совершенно случаен и не зависит от положения частицы и ее прошлой истории. Будем считать, что блуждание частицы заканчивается, как только эта частица попадет на границу ; в этом смысле граница представляет собой «поглощающий экран». Можно доказать, что с вероятностью, равной 1, блуждание точки через конечное число шагов заканчивается на границе [14, c.198].
Если частица начала свое блуждание с фиксированной внутренней точки сетки , то конечная совокупность последовательных положений этой частицы: где и , называется траекторией частицы (с шагами) или историей блуждания.
Равномерное случайное блуждание частицы на плоскости можно организовать с помощью равномерно распределенной последовательности одноразрядных случайных чисел, принимающих значения. Для этого, например, достаточно производить розыгрыш, т.е. случайную выборку из чисел ; причем числа 8 и 9 переигрываются.
Случайные числа берутся из готовых таблиц или вырабатываются электронной машиной. Последний способ при работе на счетной машине предпочтительнее, так как он позволяет не загружать сильно память машины [1, c.28].
Пусть в точках границы Г области G определена некоторая функция . Перенесем эти значения на границу сетки . Например, для каждого граничного узла определим ближайшую по горизонтали (или вертикали) точку и положим .
Для краткости введем обозначение .
Пусть — вероятность того, что траектория частицы, вышедшей из узла сетки , закончится в граничном узле . Так как блуждание точки неизбежно заканчивается на границе в первой же точке выхода ее на границу, то
где суммирование распространяется на все точки границы , причем
где — граничный узел.
где точка пробегает всю границу . Если функцию рассматривать как случайную величину, принимающую значения на границе , то сумма (4) представляет собой математическое ожидание (среднее значение) функции на границе для траекторий, начинающихся в точке («премия за выход на границу» из начальной точки ). Частица, начавшая свое случайное блуждание из внутреннего узла , после первого шага с вероятностью, равной 1/4, попадает в один из четырех соседних узлов. Поэтому случайные блуждания, начинающиеся в узле , в зависимости от вида траекторий распадаются на четыре категории новых случайных блужданий [8, c.98]:
По формуле полной вероятности имеем
Отсюда, умножая обе части равенства (5) на граничные значения и суммируя по всем возможным значениям и , на основании формулы (4) получим
Кроме того, в силу формулы (3) имеем
Рассмотрим теперь задачу Дирихле об отыскании функции , гармонической области и принимающей на ее границе заданные непрерывные значения . Согласно методу сеток эта задача сводится к нахождению значений искомой функции во внутренних узлах некоторой сетки при условии, что значения в граничных узлах известны и равны . Неизвестные определяются из системы линейных уравнений
Сравнивая формулы (8) с формулами (6), (7), мы усматриваем, что они совпадают с точностью до обозначений. Следовательно, искомые неизвестные можно рассматривать как математические ожидания . Величины допускают экспериментальное определение. Рассмотрим достаточно большое число равномерных случайных блужданий частицы по узлам сетки , исходящих из фиксированного узла и заканчивающихся на границе . Пусть соответствующие точки выхода частицы на границу . Заменяя математическое ожидание эмпирическим математическим ожиданием, будем иметь
Формула (9) дает статистическую оценку величины и может быть применена для приближенного решения задачи Дирихле. Метод решения задач, основанный на использовании случайных величин, получил общее название метода Монте-Карло [10, c.104].
Заметим, что с помощью формулы (9) можно непосредственно найти приближенное значение решения задачи Дирихле в единственной фиксированной точке сетки , не зная решения задачи для остальных точек сетки. Этим обстоятельством метод Монте-Карло для задачи Дирихле резко отличается от обычных стандартных способов решения этой задачи.
Интересно отметить, что вероятность , в силу формулы (4), представляет собой аналог функции Грина для задачи Дирихле в области. Эта величина может быть найдена экспериментально на основании формулы (9), если задать следующие граничные условия [14, c.55]:
Построив такую функцию Грина, мы получаем возможность, применяя формулу (9), просто
находить приближенное решение задачи Дирихле для области данной границей при любых граничных значениях .
Недостатком рассмотренного варианта метода Монте-Карло для задачи Дирихле является слабая сходимость по вероятности при эмпирического математического ожидания
к математическому ожиданию . Чтобы устранить это неблагоприятное обстоятельство, используют различные модификации случайных блужданий. Кроме того, при решении задачи полезно учитывать также, что блуждание частицы , начинающееся в точке автоматически является случайным блужданием частицы, начинающимся в любой промежуточной точке траектории этой частицы [4, c.129].
Укажем другой метод Монте-Карло для решения задачи Дирихле для уравнения Лапласа, не связанный с разностными уравнениями. Пусть задана ограниченная связная область и точка . Определим случайную траекторию следующим образом: положим ; далее, если точка известна, то построим окружность произвольного радиуса , расположенную внутри , и на этой окружности выберем случайную точку .
Таким образом, , где , и угол равномерно распределен в интервале .
Приведем теорему: если функция удовлетворяет в области уравнению Лапласа
то при каждом и при любых математическое ожидание равно значению в начале траектории [12, c.204].
Доказательство. Придадим более точный смысл утверждению о произвольности радиуса . Будем считать, что задана некоторая плоскость , которая тождественно равна нулю при всех , превосходящих минимальное расстояние от до границы , а также при ; случай также допускается; и выбор осуществляется в соответствии с плотностью . Пусть — плотность распределения точки в . Тогда математическое ожидание величины равно
По теореме о среднем значении гармонической функции
При точка и . Применяя индукцию, получим утверждение теоремы.
Построение траекторий рассмотренного типа в трехмерном случае иногда называют блужданием по сферам.
Приведенную выше траекторию можно использовать для приближенного решения задачи Дирихле. Пусть на границе области задана ограниченная функция . Обозначим через искомое решение, удовлетворяющее внутри уравнению (1) и обращающееся в при .
Фиксируем достаточно малую окрестность границы (рис. 3, Приложение D). Чтобы вычислить , будем строить траектории вида до тех пор, пока случайная точка не попадет в . Пусть — ближайшая к точка границы . Можем считать, что значение случайной величины приближенно равно . Построив траекторий такого типа, получим значения , по которым оценивается искомое решение
Замети, что сходимость по вероятности
когда не вытекает из теоремы Хинчина, говорящей о том, что последовательность одинаково распределенных независимых величин, у которых существуют математические ожидания, подчиняется закону больших чисел, так как в сумме (3) фигурируют различных случайных величин, различающихся правилами выбора Можно, однако воспользоваться другой формой закона больших чисел — теоремой Чебышева [14, c.150]:
Если величины независимы и существует и , то при
(Доказательство этой теоремы легко получить, применяя к величине неравенство Чебышева — ).
В нашем случае все , а дисперсии , где . В самом деле, как известно, максимум и минимум гармонической функции достигаются на границе области, так что при всех .
Такой метод расчета считается более быстрым, чем метод использования разностных уравнений, так как вдали от границы позволяет делать большие шаги . Обычно рекомендуют выбирать максимально возможные радиусы .
Данный метод был предложен Дж. Брауном и обоснован М. Мюллером, который доказал, в частности, что вероятность того, что траектория никогда не попадет в , равна нулю. Дальнейшее развитие метода — организация зависимых испытаний, решение уравнений более общего вида, использование вместо кругов других фигур (для которых известны функции Грина) [3, c.102].
Пусть — решение уравнения Лапласа в единичном квадрате , удовлетворяющее граничным условиям . Вычислить значение .
Выберем в квадрате сетку с шагом и перенумеруем узлы (рис. (4), Приложение Е). Для уравнения Лапласа формула (8) все более упрощается: , так что равно значению в том узле, в котором цепь попадает на границу.
Если случайная цифра окажется 0 или 4, то будем перемещаться в соседний узел справа, если окажется 1 или 5, то будем перемещаться влево, окажется 2 или 6, то перемещаться вверх, если окажется 3 или 7, то перемещаться вниз; значения , равные 8 или 9, опускаем.
В таблице 2 (Приложение F) приведены 16 случайных цепей. В первой строке записаны использованные случайные цифры, а в третьей — сама цепь (номера ). Соответствующие этим цепям значения равны . Среднее арифметическое этих величин дает нам приближенное значение решения в точке :
Из эмпирической оценки дисперсии
следует, что вероятная ошибка .
Точное решение рассмотренной задачи , так что , и фактическая ошибка расчета равна 0,08.
Приведенный здесь метод позволяет вычислять решения разностных уравнений, аппроксимирующих дифференциальные уравнения.
В рамках данной работы проведено изучение основных положений теории дифференциальных уравнений в частных производных, показана возможность применения вероятностных методов для их решения. В качестве примера была выбрана задача Дирихле для уравнений Лапласа и Пуассона.
Во многих областях физики, математики и других естественных наук часто используются численные и эмпирические методы для решения прямых и обратных задач. Следует отметить особую роль дифференциальных уравнений при решении таких задач, поскольку не всегда удается установить функциональную зависимость между искомыми и данными переменными величинами, но зато часто удается вывести дифференциальное уравнение, позволяющее точно предсказать протекание определенного процесса при определенных условиях.
Дифференциальные уравнения имеют огромное прикладное значение, являясь мощным орудием исследования многих задач естествознания и техники: они широко используются в механике, астрономии, физике, во многих задачах химии, биологии. Это объясняется тем, что весьма часто законы, которым подчиняются те или иные процессы, записываются в форме дифференциальных уравнений, а сами эти уравнения, таким образом, являются средством для количественного выражения этих законов.
уравнение производный задача лаплас
1.Араманович И.Г., Левин В.И. Уравнения математической физики. — М.: Наука, 1964.
2.Березин И.С., Жидков Н.П. Методы вычислений. — М.: Изд-во Государственной литературы, 1959. — 602 с.
3.Бицадзе А.В. Уравнения математической физики: Учеб. М.: Наука, 1982. 336 с.
4.Бицадзе А.В., Калиниченко Д.Ф. Сборник задач по уравнениям математической физики: Учеб. пособие. М.: Наука, 1977. 222 с.
.Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике: Учеб. пособие. М.: Наука, 1980. 686 с.
6.Бусленко Н.П., Шрейдер Ю.А. Метод статистических испытаний (Монте-Карло) и его реализация в цифровых машинах. — М.: Физматгиз, 1961. — 315 с.
7.Владимиров В.С., Уравнения математической физики, М., 1967. — 256с.
8.Голоскоков Д.П. Уравнения математической физики. Решение задач в системе Maple. — С-Пб: Питер, 2004. — 145с.
9.Демидович Б.П., Марон И.А., Шувалова Э. Численные методы анализа. — М.:Наука, 1967. — 368 с.
10.Канторович Л.В. и Крылов В.И., Приближённые методы высшего анализа, 5 изд., Л. — М., 1962. — 256с.
11.Карслоу Г.С., Теория теплопроводности, пер. с англ., М.: Приор, 2002.
.Михайлов В.П. Дифференциальные уравнения в частных производных: Учеб.пособие. М.: Наука, 1983. 424 с.
.Петровский И.Г., Лекции по теории интегральных уравнений, 3 изд., М., 1999. — 213с.
14.Сдвижников О.А., Математика на компьютере: Maple8. М.: Солон-Пресс, 2003. -176 с.
.Смирнов В.И. Курс высшей математики: Учеб.: В 4 т. Т.2. М.: Наука, 1981. 655 с.
16.Соболь И.М. Численные методы Монте-Карло. — М.: Наука, 1973. — 312 с.
17.Тихоненко А.В. Компьютерные математические пакеты в курсе «Линейные и нелинейные уравнения физики». Обнинск: ИАТЭ, 2005.- 80 с.
18.Тихонов А.Н., Самарский А.А. Уравнения математической физики: Учеб.Пособие. М.: Наука, 1977. 735 с.
Теги: Дифференциальные уравнения в частных производных Курсовая работа (теория) Математика
http://www.bestreferat.ru/referat-244220.html
http://dodiplom.ru/ready/129001