Линейные диофантовы уравнения двумя переменными

Линейные диофантовы уравнения с двумя переменными

Калькулятор решает линейные диофантовы уравнения с двумя переменными.

Сначала калькулятор, теория под ним.

Линейные диофантовы уравнения с двумя переменными

Диофантово уравнение с двумя неизвестными имеет вид:

где a, b, c — заданные целые числа, x и y — неизвестные целые числа.

Для нахождения решений уравнения используется Расширенный алгоритм Евклида (исключая вырожденный случай, когда a = b = 0 и уравнение имеет либо бесконечно много решений, либо же не имеет решений вовсе).
Если числа a и b неотрицательны, тогда с помощью расширенного алгоритма Евклида мы можем найти их наибольший общий делитель g, а также такие коэффициенты и , что:
.

Утверждается, что если число c делится на g, то диофантово уравнение имеет решение; в противном случае диофантово уравнение решений не имеет. Это следует из очевидного факта, что линейная комбинация двух чисел по-прежнему должна делиться на их общий делитель.

То есть если c делится на g, тогда выполняется соотношение:

т. е. одним из решений диофантова уравнения являются числа:

Если одно из чисел a и b или они оба отрицательны, то можно взять их по модулю и применить к ним алгоритм Евклида, как было описано выше, а затем изменить знак найденных коэффициентов и в соответствии с настоящим знаком чисел a и b соответственно.

Если мы знаем одно из решений, мы можем получить выражение для всех остальных решений, которых бесконечное множество.

Итак, пусть g = НОД (a,b), выполняется условие:
.

Тогда, прибавив к число и одновременно отняв от , мы не нарушим равенства:

Этот процесс можно повторять сколько угодно, т. е. все числа вида:

,
где k принадлежит множеству целых чисел, являются множеством всех решений диофантова уравнения.

Линейное диофантово уравнение и 4 способа его решения

Разделы: Математика

Првило 1. Если с не делится на d, то уравнение ах + ву = с не имеет решений в целых числах. Н.О.Д.(а,в) = d.

Правило 2. Чтобы найти решение уравнения ах + ву = с при взаимно-простых а и в, нужно сначала найти решение (Х_о ; у_о) уравнения ах + ву = 1; числа СХ_о , Су_о составляют решение уравнения ах + ву = с.

Решить в целых числах (х,у) уравнение

Первый способ. Нахождение частного решения методом подбора и запись общего решения.

Знаем, что если Н.О.Д.(а;в) =1, т.е. а и в взаимно-простые числа, то уравнение (1)

имеет решение в целых числах х и у. Н.О.Д.(5;8) =1. Методом подбора находим частное решение: Х_о = 7; у_о =2.

Итак, пара чисел (7;2) — частное решение уравнения (1).

Значит, выполняется равенство: 5 x 7 – 8 x 2 = 19 … (2)

Вопрос: Как имея одно решение записать все остальные решения?

Вычтем из уравнения (1) равенство (2) и получим: 5(х -7) – 8(у — 2) =0.

Отсюда х – 7 = . Из полученного равенства видно, что число (х – 7) будет целым тогда и только тогда, когда (у – 2) делится на 5, т.е. у – 2 = 5n, где n какое-нибудь целое число. Итак, у = 2 + 5n, х = 7 + 8n, где n Z.

Тем самым все целые решения исходного уравнения можно записать в таком виде:

n Z.

Второй способ. Решение уравнения относительно одного неизвестного.

Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. 5х — 8у = 19 х = .

Остатки при делении на 5: 0,1,2,3,4. Подставим вместо у эти числа.

Если у = 0, то х = =.

Если у =1, то х = =.

Если у = 2, то х = = = 7 Z.

Если у =3, то х = =.

Если у = 4 то х = =.

Итак, частным решением является пара (7;2).

Тогда общее решение: n Z.

Третий способ. Универсальный способ поиска частного решения.

Для решения применим алгоритм Евклида. Мы знаем, что для любых двух натуральных чисел а, в, таких, что Н.О.Д.(а,в) = 1 существуют целые числа х,у такие, что ах + ву = 1.

1. Сначала решим уравнение 5m – 8n = 1 используя алгоритм Евклида.

2. Затем найдем частное решение уравнения (1)по правилу 2.

3. Запишем общее решение данного уравнения (1).

1. Найдем представление: 1 = 5m – 8n. Для этого используем алгоритм Евклида.

8 = 5 1 + 3.

5 = 3

3 = 2 .

Из этого равенства выразим 1. 1 = 3 — 2 = 3 – (5 — 3 ) =

= 3 — 5 = 3 = (8 — 5 — 5 82 -5

= 5(-2). Итак, m = -3, n = -2.

2. Частное решение уравнения (1): Х_о = 19m; у_о =19n.

Отсюда получим: Х_о =19; у_о =19 .

Пара (-57; -38)- частное решение (1).

3. Общее решение уравнения (1): n Z.

Четвертый способ. Геометрический.

1. Решим уравнение 5х – 8у = 1 геометрически.

2. Запишем частное решение уравнения (1).

3. Запишем общее решение данного уравнения (1).

Отложим на окружности последовательно друг за другом равные дуги, составляющие

-ю часть полной окружности. За 8 шагов получим все вершины правильного вписанного в окружность 8-угольника. При этом сделаем 5 полных оборотов.

На 5 – ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли — ю часть окружности, так что х = у + .

Итак, Х_о = 5, у_о =3 является частным решением уравнения 5х – 8у = 1.

2. Частное решение уравнения (1): Х_о = 19 у_о =19

3. Общее решение уравнения (1): n Z.

Линейные диофантовы уравнения

Линейные диофантовы уравнения и методы их решения в школьном курсе математики не изучаются. Их можно встретить, в основном, лишь в олимпиадных заданиях. В данной работе рассматриваются следующие способы решения линейных диофантовых уравнений: алгоритм Евклида, метод перебора, метод спуска, метод рассмотрения остатков от деления, а также приведены примеры решения линейных диофантовых уравнений с тремя неизвестными.

Просмотр содержимого документа
«Линейные диофантовы уравнения»

Линейные диофантовы уравнения

Исследовательская работа по алгебре

ученика 9 класса МОУ «Упшинская ООШ»

«Если вы хотите научиться плавать, то

смело входите в воду, а если хотите

научиться решать задачи, то решайте их.»

Руководитель – Софронова Н.А .

Для настилки пола шириной в 3 метра имеются доски шириной в 11 см и 13 см. Сколько нужно взять досок того и другого размера?

Если х – число досок шириной в 11 см, а у – число досок шириной в 13 см, то нам надо решить уравнение:

Особенности уравнения 11 х + 13 у = 300: ▪ Коэффициенты 11, 13, 300 – целые числа. ▪ Число неизвестных превышает число уравнений. ▪ Решения данного уравнения х и у должны быть целыми положительными числам

Алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, в которых число неизвестных превышает число уравнений и для которых надо найти целые решения, называют неопределенными или диофантовыми, по имени греческого математика Диофанта .

Примеры диофантовых уравнений

1 . Найдите все пары целых чисел

2 . Покажите, что уравнение

имеет бесконечное множество решений

• Всегда ли можно найти для конкретного неопределенного уравнения все целые решения или доказать отсутствие таковых?

• Какиеметодысуществуютдлярешения диофантовых уравнений?

• Найти и изучить методы решениялинейныхдиофантовых уравнений с двумя переменными.

• Рассмотреть возможности теории линейных диофантовых уравнений.

• Неопределенные уравнения в целых числах решались еще до Диофанта. Большой интерес вызывало, например, алгебраическое уравнениеx2+y2=z2,связывающее стороныx,у,zпрямоугольного треугольника. Натуральные числаx,yиz, являющиеся решениями этого уравнения, называются«пифагоровыми тройками».

• К работам Диофанта имеют непосредственное отношение и математические исследования французского математика Пьера Ферма. Считается, что именно с работ Ферма началась новая волна в развитии теории чисел. И одна из его задач — это знаменитое уравнение Ферма

Ни один крупный математик не прошел мимо теории диофантовых уравнений.

Ферма, Эйлер, Лагранж, Гаусс, Чебышев оставили неизгладимый след в этой интересной теории.

1, ( Каталана); ах 2 + bxy + су 2 + dx + еу + f = 0 , где а , b , с , d , е , f — целые числа, т. е. общее неоднородное уравнение второй степени с двумя неизвестными (П.Ферма, Дж. Валлис, Л. Эйлер, Ж. Лагранж и К.Гаусс) » width=»640″

Диофантовы уравнения в 20 веке

1900 год. Международный математический конгресс.

10-я проблема Гильберта

Задано Диофантово уравнение с некоторым числом неизвестных и рациональными целыми коэффициентами. Необходимо придумать процедуру, которая могла определить за конечное число операций – является ли уравнение разрешимым в рациональных целых числах.

Русский математик Юрий Матиясевич доказал :

10-ая проблема Гильберта неразрешима — требуемого в ней алгоритма не существует.

Всегда ли можно найти для конкретного неопределенного уравнения все целые решения или доказать отсутствие таковых?

• Проблема решения уравнений в целых числах решена до конца только для уравнений первой степени с двумя или тремя неизвестными.
• ДУ второй степени с двумя неизвестными решаются уже с большим трудом.
• ДУ второй степени с числом неизвестных больше двух решены лишь в отдельных частных случаях, например уравнениеx2+y2=z2.
• ДУ степени выше второй имеют, как правило, лишь конечное число решений (в целых числах).
• Для уравнений выше второй степени с двумя или более неизвестными достаточно трудной является даже задача существования целочисленных решений. Например, неизвестно, имеет ли уравнение

• Для решения отдельных ДУ, а иногда и для конкретных уравнений, приходится изобретать новые методы. Очевидно, что алгоритма, который позволял бы находить решения произвольных ДУ не существует.

Линейные диофантовы уравнения

ЛДУ с двумя переменными:

ЛДУ с тремя переменными:

ЛДУ с двумя неизвестными

ЛДУ с двумя переменными:

Поиск частного решения

• Метод кратных.
• Применение алгоритма Евклида.
• Метод перебора.
• Метод спуска.

• Метод рассмотрения остатков от деления
• Метод рассмотрения остатков от деления

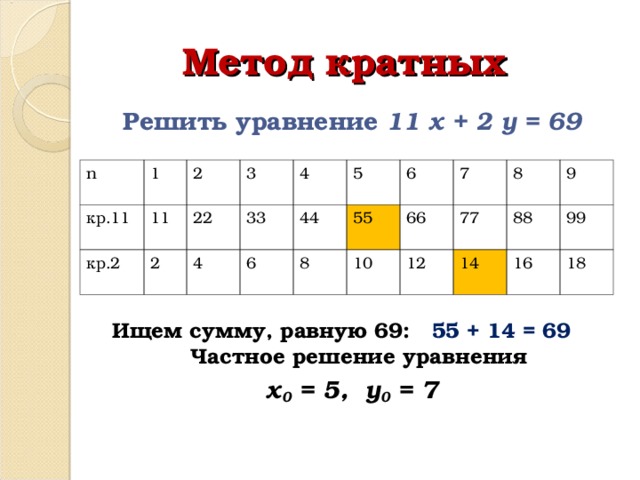
Решить уравнение 11 х + 2 у = 69

Ищем сумму, равную 69: 55 + 14 = 69 Частное решение уравнения

Применение алгоритма Евклида

Решить уравнение 4 х + 7 у = 16

• Найдем НОД чисел 4 и 7 по алгоритму Евклида : НОД(4,7) =1

• Выразим число1через коэффициентыа= 4 иb=7, используя теорему о линейном разложении НОД:

Решить уравнение 7 х + 12 у = 100

Метод спуска: 3х+8у=60

Метод рассмотрения остатков от деления

• Решить в целых числах уравнение3х – 4у = 1
• 3 х = 4 у + 1
• Левая часть уравнения делится на 3, значит и правая должна делиться на 3. При делении на 3 могут получиться остатки 0, 1, и 2.
• Рассмотрим 3 случая.

3 x = 4 ∙ 3p + 1 = 12 p + 1

Не делится на 3

3 x = 4 ∙ (3p + 1) +1 = 12 p + 3

Не делится на 3

3 x = 4 ∙ (3p + 2) +1 = 12 p + 9

Что дала мне работа над проектом?

• Получил представление о работе над исследовательским проектом.
• Познакомился с историей развития диофантовых уравнений и биографией Диофанта.
• Изучил методы решения ЛДУ с двумя и тремя неизвестными.
• решил группу задач, которые носят практический характер, а также встречаются на олимпиадах, экзаменах за курс основной школы
• Приобрел навыки решения нестандартных задач.

Думаю, что в последующем я продолжу изучение диофантовых уравнений второй степени и методов их решения.