Линейные диофантовы уравнения примеры для решения

Линейное диофантово уравнение и 4 способа его решения

Разделы: Математика

Првило 1. Если с не делится на d, то уравнение ах + ву = с не имеет решений в целых числах. Н.О.Д.(а,в) = d.

Правило 2. Чтобы найти решение уравнения ах + ву = с при взаимно-простых а и в, нужно сначала найти решение (Х_о ; у_о) уравнения ах + ву = 1; числа СХ_о , Су_о составляют решение уравнения ах + ву = с.

Решить в целых числах (х,у) уравнение

Первый способ. Нахождение частного решения методом подбора и запись общего решения.

Знаем, что если Н.О.Д.(а;в) =1, т.е. а и в взаимно-простые числа, то уравнение (1)

имеет решение в целых числах х и у. Н.О.Д.(5;8) =1. Методом подбора находим частное решение: Х_о = 7; у_о =2.

Итак, пара чисел (7;2) — частное решение уравнения (1).

Значит, выполняется равенство: 5 x 7 – 8 x 2 = 19 … (2)

Вопрос: Как имея одно решение записать все остальные решения?

Вычтем из уравнения (1) равенство (2) и получим: 5(х -7) – 8(у — 2) =0.

Отсюда х – 7 = . Из полученного равенства видно, что число (х – 7) будет целым тогда и только тогда, когда (у – 2) делится на 5, т.е. у – 2 = 5n, где n какое-нибудь целое число. Итак, у = 2 + 5n, х = 7 + 8n, где n Z.

Тем самым все целые решения исходного уравнения можно записать в таком виде:

n Z.

Второй способ. Решение уравнения относительно одного неизвестного.

Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. 5х — 8у = 19 х = .

Остатки при делении на 5: 0,1,2,3,4. Подставим вместо у эти числа.

Если у = 0, то х = =.

Если у =1, то х = =.

Если у = 2, то х = = = 7 Z.

Если у =3, то х = =.

Если у = 4 то х = =.

Итак, частным решением является пара (7;2).

Тогда общее решение: n Z.

Третий способ. Универсальный способ поиска частного решения.

Для решения применим алгоритм Евклида. Мы знаем, что для любых двух натуральных чисел а, в, таких, что Н.О.Д.(а,в) = 1 существуют целые числа х,у такие, что ах + ву = 1.

1. Сначала решим уравнение 5m – 8n = 1 используя алгоритм Евклида.

2. Затем найдем частное решение уравнения (1)по правилу 2.

3. Запишем общее решение данного уравнения (1).

1. Найдем представление: 1 = 5m – 8n. Для этого используем алгоритм Евклида.

8 = 5 1 + 3.

5 = 3

3 = 2 .

Из этого равенства выразим 1. 1 = 3 — 2 = 3 – (5 — 3 ) =

= 3 — 5 = 3 = (8 — 5 — 5 82 -5

= 5(-2). Итак, m = -3, n = -2.

2. Частное решение уравнения (1): Х_о = 19m; у_о =19n.

Отсюда получим: Х_о =19; у_о =19 .

Пара (-57; -38)- частное решение (1).

3. Общее решение уравнения (1): n Z.

Четвертый способ. Геометрический.

1. Решим уравнение 5х – 8у = 1 геометрически.

2. Запишем частное решение уравнения (1).

3. Запишем общее решение данного уравнения (1).

Отложим на окружности последовательно друг за другом равные дуги, составляющие

-ю часть полной окружности. За 8 шагов получим все вершины правильного вписанного в окружность 8-угольника. При этом сделаем 5 полных оборотов.

На 5 – ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли — ю часть окружности, так что х = у + .

Итак, Х_о = 5, у_о =3 является частным решением уравнения 5х – 8у = 1.

2. Частное решение уравнения (1): Х_о = 19 у_о =19

3. Общее решение уравнения (1): n Z.

Алгебра. 7 класс

Конспект урока

Линейные диофантовы уравнения

Перечень рассматриваемых вопросов:

• Диофантово уравнение.
• Разрешимость диофантова уравнения.
• Решение задач с помощью диофантова уравнения.

Диофантовым уравнением называется уравнение вида ах + bу = с (а ≠ 0, b ≠ 0), где а, b, с, х и у – целые числа.

Если c делится на НОД(а; b), то уравнение ах + bу = с имеет решение в целых числах. Если c не делится на НОД (а; b), то уравнение ах + bу = с не имеет решений в целых числах.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Определение диофантова уравнения.

Пусть дано уравнение ах + bу = с (а ≠ 0, b ≠ 0), где а, b, с – целые числа. Если поставлена задача найти только такие его решения (х₀; у₀), где х_0, у₀ – целые числа, то это уравнение называют линейным диофантовым уравнением.

Диофантовы уравнения связаны с именем древнегреческого математика Диофанта Александрийского. О подробностях жизни Диофанта Александрийского практически ничего не известно. С одной стороны, Диофант цитирует Гипсикла (II век до нашей эры); с другой стороны, о Диофанте пишет Теон Александрийский (около 350 года нашей эры). Откуда можно сделать вывод, что жил он приблизительно в III веке нашей эры.

Решение диофантовых уравнений.

Решим линейное диофантово уравнение

Выразим у через х:

Из этого равенства видно, что у будет целым только тогда, когда целое число х делится на 3, т.е. х = 3х_1, где х_{1 –} некоторое целое число. Тогда у = 2 -2х₁.

Таким образом, решениями уравнения являются все пары чисел (3х_1;2 -2х₁).

Приведём некоторые частные решения этого уравнения.

Если х₁ = 0, то х = 3х_{1 =} 0, а у = 2 — 2 х₁ = 2; решением уравнения является пара (0;2).

Если х_{1 =} 1, то х = 3х_{1 =} 3, а у = 2 — 2 х₁ = 0;

решением уравнения является пара (3; 0)

Аналогично можно найти и другие частные решения, их бесконечно много.

Решение задач при помощи линейных диофантовых уравнений.

Линейные диофантовы уравнения возникают при решении некоторых задач.

У покупателя и продавца имеются монеты только по 2р. и 5р. Сможет ли покупатель заплатить за покупку стоимостью 1р.?

Если покупатель даст х монет по 2р. и у монет по 5 р., то он заплатит (2х + 5у) р. А по условию задачи это 1р. Составим уравнение:

Выразим х через у из уравнения:

Из равенства видно, что х будет целым только тогда, когда у будет нечетным числом: у = 2m + 1, где m – целое число.

Таким образом, решением уравнения являются все пары чисел (-5m – 2; 2m + 1), где m – любое целое число.

Таким образом, способов оплаты товара стоимостью 1р. Бесконечно много. Если х окажется отрицательным, то это означает, что покупатель должен получить сдачу: х монет по 2р.

Например, пара (-2; 1) является решением уравнения. Это означает, что покупатель далодну монету по 5 р. и получил сдачу 2 монеты по 2р.

Разрешимость диофантова уравнения.

Не каждое диофантово уравнение имеет решение в целых числах.

Рассмотрим на примере уравнения

3х + 6у = 2 алгоритм, с помощью которого можно определить, имеет оно решение в целых числах.

1 шаг. Надо найти наибольший общий делитель чисел 3 и 6. НОД(3; 6) = 3.

2 шаг. Определить, делится ли 2 на НОД(3; 6).

3 шаг. Если 2 делится на НОД(3; 6), то уравнение имеет решение в целых числах.

Если 2 не делится на НОД (3; 6), то уравнение не имеет решений в целых числах.

Расширенный алгоритм Евклида для решения диофантовых уравнений.

Для нахождения наибольшего общего делителя двух целых неотрицательных чисел используют алгоритм Евклида. Рассмотрим его реализацию на примере чисел 24 и 17.

Разделим большее из этих чисел на меньшее, то есть 24 на 17.

Получаем 24 : 17 = 1 (ост. 7), что можно записать в виде равенства:

Теперь разделим делитель на остаток, то есть 17 на 7, получим:

Снова разделим делитель на остаток:

Выполним деление еще раз:

Мы получили остаток, равный нулю, так как 3 делится на 1 без остатка.

В представленной последовательности действий мы получали остатки: 7, 3, 1, 0. Последний остаток, не считая 0, является наибольшим общим делителем чисел 24 и 17. То есть, НОД(24; 17) = 1.

Рассмотрим еще один пример: НОД(612; 342)?

612 = 342 ∙ 1 + 270,

342 = 270 ∙ 1 + 72,

Теперь выполним действия «в обратном направлении», то есть выразим 18 (остаток) через числа 612 и 342.

Для этого в каждой строчке последовательности Евклида выразим остатки через делимое и делитель (второй столбик таблицы):

612 = 342 ∙ 1 + 270

342 = 270 ∙ 1 + 72

270 = 612 – 342 ∙ 1

72 = 342 – 270 ∙ 1

Получаем, 18 = 72 – 54 ∙ 1 = 72 – (270 – 72 ∙ 3) = 342 – 270 ∙ 1 – (270 – (342 — 270 ∙ 1) ∙3) =

342 – ((612 – 342 ∙1) ∙ 1) – (612 – 342 ∙ 1 – (342 – (612 – 342 ∙ 1)) ∙3) = 342 – 612 + 342 – 612 + 342 + 342 ∙ 3 – 612 ∙ 3 + 342 ∙ 3 = 342 ∙ 9 – 612 ∙ 5 = 342 ∙ 9 + 612 ∙ (-5).

То есть 18 = 9 ∙ 342 + (-5) ∙ 612.

Умение выполнять действия алгоритма «в обратном направлении» понадобится нам в решении диофантовых уравнений при помощи расширенного алгоритма Евклида.

Пример: решите уравнение 24x−17y=2.

Найдем при помощи алгоритма Евклида НОД(24, 17):

Выполним действия «в обратном направлении»:

1 = 7 – 3 · 2 = 7 − (17 – 7 · 2) · 2 = 7 – 17 · 2 + 7 · 4 + 5 · 7 – 2 · 17 = 5 · (24 – 17 · 1) – 2 · 17 = 5 · 24 – 5 · 17 – 2 · 17 = 5 · 24 – 7 · 17 = 24 · 5 – 17 · 7.

24 · 5 – 17 · 7 = 1; В исходном уравнении в правой части стоит число 2. Поэтому умножим обе части уравнения на 2. Получим:

24 · 10 – 17 · 14 = 2.

То есть, x₀ = 10, y₀ = 14 – частные решения уравнения 24x −17y = 2.Если уравнение имеет одно решение в целых числах, то оно имеет бесконечное множество других решений.

Прибавим коэффициент b к значению х.

Чтобы значение исходного уравнения не изменилось, при прибавлении одного числа к х нужно вычесть другое число изу:

(-7; -10) – еще одно решение уравнения.

Значения x будут равны сумме исходного решения (х₀) и любого кратного коэффициента b. То есть х = 10 + (-17t), где t – целое число.

А значение у – равны разности у₀ и любого кратного коэффициента а. То есть у = 14 – 24t.

Ответ: (10 − 17t, 14 − 24t), t ∈ Z.

Разбор заданий тренировочного модуля.

1. Решите задачу:

Некий чиновник купил ослов и быков за 1770 талеров. За каждого осла он уплатил по 31 талеру, а за каждого быка – по 21 талеру. Сколько ослов и быков купил чиновник?

Пусть чиновник купил х ослов и у быков. Тогда 31х + 21у = 1770.

По смыслу задачи х и у – натуральные числа. Так как 21 и 1770 делятся на 3, то 31х делится на 3, т. е. х делится на 3: х = 3n, где n – натуральное число. Тогда 31n + 7у = 590. Откуда n =

Очевидно, что n будет целым, если 7у – 1 делится на 31.

Наименьшее натуральное у, при котором это произойдет, равно 9. При этом n = 17, х = 51. Первое решение найдено: (51; 9).

Заметим, что следующие целые n будут получаться в результате увеличения у = 9 на число, кратное 31.

При у = 9 + 21 = 40 имеем n = 10, х = 30.

При у = 40 + 9 имеем n = 3, х = 9.

При следующих значениях у значения n отрицательны. Таким образом, исходное уравнение имеет 3 решения: (51, 9), (30, 40), (9, 71).

Ответ: (51, 9), (30, 40), (9, 71).

2. Решение уравнения.

Разделите уравнения на 2 группы: уравнение имеет решение в целых числах, уравнение не имеет решений в целых числах.

1) НОД(7; 5) = 1, 2 делится на 1, следовательно, 7х – 5у = 2 имеет решение в целых числах.

2) НОД(3; 5) = 1, 10 делится на 1, следовательно, 3х + 5у = 10 имеет решение в целых числах.

3) НОД(2; 4) = 2, -1 не делится на 2, следовательно, 2х + 4у = -1 не имеет решений в целых числах.

4) НОД(3; 9) = 3, 10 не делится на 3, следовательно, 3х – 9у = 10 не имеет решений в целых числах.

5) НОД(6; 9) = 3, 2 не делится на 3, следовательно, 6х + 9у = 2 не имеет решений в целых числах.

6) НОД(2; 5) = 1, 15 делится на 1, следовательно, 2х – 5у = 15 имеет решение в целых числах.

Линейные диофантовы уравнения

Линейные диофантовы уравнения и методы их решения в школьном курсе математики не изучаются. Их можно встретить, в основном, лишь в олимпиадных заданиях. В данной работе рассматриваются следующие способы решения линейных диофантовых уравнений: алгоритм Евклида, метод перебора, метод спуска, метод рассмотрения остатков от деления, а также приведены примеры решения линейных диофантовых уравнений с тремя неизвестными.

Просмотр содержимого документа
«Линейные диофантовы уравнения»

Линейные диофантовы уравнения

Исследовательская работа по алгебре

ученика 9 класса МОУ «Упшинская ООШ»

«Если вы хотите научиться плавать, то

смело входите в воду, а если хотите

научиться решать задачи, то решайте их.»

Руководитель – Софронова Н.А .

Для настилки пола шириной в 3 метра имеются доски шириной в 11 см и 13 см. Сколько нужно взять досок того и другого размера?

Если х – число досок шириной в 11 см, а у – число досок шириной в 13 см, то нам надо решить уравнение:

Особенности уравнения 11 х + 13 у = 300: ▪ Коэффициенты 11, 13, 300 – целые числа. ▪ Число неизвестных превышает число уравнений. ▪ Решения данного уравнения х и у должны быть целыми положительными числам

Алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, в которых число неизвестных превышает число уравнений и для которых надо найти целые решения, называют неопределенными или диофантовыми, по имени греческого математика Диофанта .

Примеры диофантовых уравнений

1 . Найдите все пары целых чисел

2 . Покажите, что уравнение

имеет бесконечное множество решений

• Всегда ли можно найти для конкретного неопределенного уравнения все целые решения или доказать отсутствие таковых?

• Какиеметодысуществуютдлярешения диофантовых уравнений?

• Найти и изучить методы решениялинейныхдиофантовых уравнений с двумя переменными.

• Рассмотреть возможности теории линейных диофантовых уравнений.

• Неопределенные уравнения в целых числах решались еще до Диофанта. Большой интерес вызывало, например, алгебраическое уравнениеx2+y2=z2,связывающее стороныx,у,zпрямоугольного треугольника. Натуральные числаx,yиz, являющиеся решениями этого уравнения, называются«пифагоровыми тройками».

• К работам Диофанта имеют непосредственное отношение и математические исследования французского математика Пьера Ферма. Считается, что именно с работ Ферма началась новая волна в развитии теории чисел. И одна из его задач — это знаменитое уравнение Ферма

Ни один крупный математик не прошел мимо теории диофантовых уравнений.

Ферма, Эйлер, Лагранж, Гаусс, Чебышев оставили неизгладимый след в этой интересной теории.

1, ( Каталана); ах 2 + bxy + су 2 + dx + еу + f = 0 , где а , b , с , d , е , f — целые числа, т. е. общее неоднородное уравнение второй степени с двумя неизвестными (П.Ферма, Дж. Валлис, Л. Эйлер, Ж. Лагранж и К.Гаусс) » width=»640″

Диофантовы уравнения в 20 веке

1900 год. Международный математический конгресс.

10-я проблема Гильберта

Задано Диофантово уравнение с некоторым числом неизвестных и рациональными целыми коэффициентами. Необходимо придумать процедуру, которая могла определить за конечное число операций – является ли уравнение разрешимым в рациональных целых числах.

Русский математик Юрий Матиясевич доказал :

10-ая проблема Гильберта неразрешима — требуемого в ней алгоритма не существует.

Всегда ли можно найти для конкретного неопределенного уравнения все целые решения или доказать отсутствие таковых?

• Проблема решения уравнений в целых числах решена до конца только для уравнений первой степени с двумя или тремя неизвестными.
• ДУ второй степени с двумя неизвестными решаются уже с большим трудом.
• ДУ второй степени с числом неизвестных больше двух решены лишь в отдельных частных случаях, например уравнениеx2+y2=z2.
• ДУ степени выше второй имеют, как правило, лишь конечное число решений (в целых числах).
• Для уравнений выше второй степени с двумя или более неизвестными достаточно трудной является даже задача существования целочисленных решений. Например, неизвестно, имеет ли уравнение

• Для решения отдельных ДУ, а иногда и для конкретных уравнений, приходится изобретать новые методы. Очевидно, что алгоритма, который позволял бы находить решения произвольных ДУ не существует.

Линейные диофантовы уравнения

ЛДУ с двумя переменными:

ЛДУ с тремя переменными:

ЛДУ с двумя неизвестными

ЛДУ с двумя переменными:

Поиск частного решения

• Метод кратных.
• Применение алгоритма Евклида.
• Метод перебора.
• Метод спуска.

• Метод рассмотрения остатков от деления
• Метод рассмотрения остатков от деления

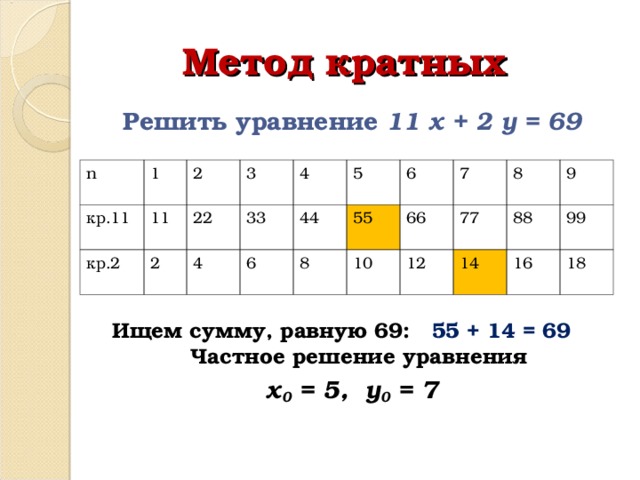
Решить уравнение 11 х + 2 у = 69

Ищем сумму, равную 69: 55 + 14 = 69 Частное решение уравнения

Применение алгоритма Евклида

Решить уравнение 4 х + 7 у = 16

• Найдем НОД чисел 4 и 7 по алгоритму Евклида : НОД(4,7) =1

• Выразим число1через коэффициентыа= 4 иb=7, используя теорему о линейном разложении НОД:

Решить уравнение 7 х + 12 у = 100

Метод спуска: 3х+8у=60

Метод рассмотрения остатков от деления

• Решить в целых числах уравнение3х – 4у = 1
• 3 х = 4 у + 1
• Левая часть уравнения делится на 3, значит и правая должна делиться на 3. При делении на 3 могут получиться остатки 0, 1, и 2.
• Рассмотрим 3 случая.

3 x = 4 ∙ 3p + 1 = 12 p + 1

Не делится на 3

3 x = 4 ∙ (3p + 1) +1 = 12 p + 3

Не делится на 3

3 x = 4 ∙ (3p + 2) +1 = 12 p + 9

Что дала мне работа над проектом?

• Получил представление о работе над исследовательским проектом.
• Познакомился с историей развития диофантовых уравнений и биографией Диофанта.
• Изучил методы решения ЛДУ с двумя и тремя неизвестными.
• решил группу задач, которые носят практический характер, а также встречаются на олимпиадах, экзаменах за курс основной школы
• Приобрел навыки решения нестандартных задач.

Думаю, что в последующем я продолжу изучение диофантовых уравнений второй степени и методов их решения.