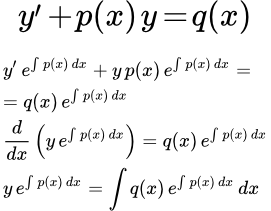Линейные неоднородные уравнения первого порядка с примерами

Решение линейных дифференциальных уравнений первого порядка

Определения и методы решений

Линейное дифференциальное уравнение первого порядка – это уравнение вида
,
где p и q – функции переменной x .

Линейное однородное дифференциальное уравнение первого порядка – это уравнение вида
.

Линейное неоднородное дифференциальное уравнение первого порядка – это уравнение вида
.

Член q ( x ) называется неоднородной частью уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

Решение линейного дифференциального уравнения с помощью интегрирующего множителя

Рассмотрим метод решения линейного дифференциального уравнения первого порядка с помощью интегрирующего множителя.
Умножим обе части исходного уравнения (1) на интегрирующий множитель
:
(2)
Далее замечаем, что производная от интеграла равна подынтегральной функции:

По правилу дифференцирования сложной функции:

По правилу дифференцирования произведения:

Подставляем в (2):

Интегрируем:

Умножаем на . Получаем общее решение линейного дифференциального уравнения первого порядка:

Пример решения линейного дифференциального уравнения первого порядка

Разделим обе части исходного уравнения на x :
(i) .
Тогда
;
.
Интегрирующий множитель:

Знак модуля можно опустить, поскольку интегрирующий множитель можно умножать на любую постоянную (в том числе на ± 1 ).
Умножим (i) на x 3 :
.
Выделяем производную.
;
.
Интегрируем, применяя таблицу интегралов:
.
Делим на x 3 :
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 22-07-2012 Изменено: 25-02-2015

Линейные неоднородные дифференциальные уравнения первого порядка

В данной теме поговорим о способах решения линейных неоднородных дифференциальных уравнений вида y ‘ = P ( x ) · y = Q ( x ) . Начнем с метода вариации произвольной постоянной и покажем способ применения этого метода для решения задачи Коши. Продолжим рассмотрением метода, который предполагает представление произвольной постоянной у как произведения двух функций u ( x ) и v ( x ) . В разделе мы приводим большое количество задач по теме с детальным разбором решения.

На тот случай, если применяемые при разборе темы термины и понятия окажутся незнакомыми для вас, мы рекомендуем заглядывать в раздел «Основные термины и определения теории дифференциальных уравнений».

Метод вариации произвольной постоянной для решения ЛНДУ первого порядка

Для краткости будет обозначать линейное неоднородное дифференциальное уравнение аббревиатурой ЛНДУ, а линейное однородное дифференциальное уравнение (ЛОДУ).

ЛНДУ вида y ‘ = P ( x ) · y = Q ( x ) соответствует ЛОДУ вида y ‘ = P ( x ) · y = 0 , при Q ( x ) = 0 . Если посмотреть на дифференциальное уравнение y ‘ = P ( x ) · y = 0 , становится понятно, что мы имеем дело с уравнением с разделяющимися переменными. Мы можем его проинтегрировать: y ‘ = P ( x ) · y = 0 ⇔ d y y = — P ( x ) d x , y ≠ 0 ∫ d y y = — ∫ P ( x ) d x ⇔ ln y + C 1 = — ∫ P ( x ) d x ⇔ ln y = ln C — ∫ P ( x ) d x , ln C = — C 1 , C ≠ 0 ⇔ e ln y = e ln C — ∫ P ( x ) d x ⇔ y = C · e — ∫ P ( x ) d x

Мы можем утверждать, что значение переменной y = 0 тоже является решением, так как при этом значении переменной уравнение y ‘ = P ( x ) · y = 0 обращается в тождество. Этому случаю соответствует решение y = C · e — ∫ P ( x ) d x при значении C = 0 .

Получается, что y = C · e — ∫ P ( x ) d x — общее решение ЛОДУ, где С – произвольная постоянная.

y = C · e — ∫ P ( x ) d x — это решение ЛОДУ y ‘ = P ( x ) · y = 0 .

Для того, чтобы найти общее решение неоднородного уравнения y ‘ = P ( x ) · y = Q ( x ) , будем считать С не константой, а функцией аргумента х . Фактически, мы примем y = C ( x ) · e — ∫ P ( x ) d x общим решением ЛНДУ.

Подставим y = C ( x ) · e — ∫ P ( x ) d x в дифференциальное уравнение y ‘ = P ( x ) · y = Q ( x ) . Оно при этом обращается в тождество:

y ‘ = P ( x ) · y = Q ( x ) C x · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x )

Теперь обратимся к правилу дифференцирования произведения. Получаем:

C ‘ ( x ) · e — ∫ P ( x ) d x + C ( x ) · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x )

Производная сложной функции e — ∫ P ( x ) d x ‘ равна e — ∫ P ( x ) d x · — ∫ P ( x ) d x ‘ .

Теперь вспомним свойства неопределенного интеграла. Получаем:

e — ∫ P ( x ) d x · — ∫ P ( x ) d x ‘ = — e — ∫ P ( x ) d x · P ( x )

Теперь выполним переход:

C ‘ ( x ) · e — ∫ P ( x ) d x + C ( x ) · e — ∫ P ( x ) d x ‘ + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x ) C ‘ ( x ) · e — ∫ P ( x ) d x — P ( x ) · C ( x ) · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x ) C ‘ ( x ) · e — ∫ P ( x ) d x = Q ( x )

Так мы пришли к простейшему дифференциальному уравнению первого порядка. В ходе решения этого уравнения мы определим функцию C ( x ) . Это позволит нам записать решение исходного ЛНДУ первого порядка следующим образом:

y = C ( x ) · e — ∫ P ( x ) d x

Подведем итог

Метод вариации произвольной постоянной при решении ЛНДУ предполагает проведение трех этапов:

• нахождение общего решения соответствующего ЛОДУ y ‘ + P ( x ) · y = 0 в виде y = C · e — ∫ P ( x ) d x ;
• варьирование произвольной постоянной С , что заключается в замене ее функцией С ( x ) ;
• подстановка функции y = C ( x ) · e — ∫ P ( x ) d x в исходное дифференциальное уравнение, откуда мы можем вычислить C ( x ) и записать ответ.

Теперь применим этот алгоритм к решению задачи.

Найдите решение задачи Коши y ‘ — 2 x y 1 + x 2 = 1 + x 2 , y ( 1 ) = 3 .

Нам нужно отыскать частное решение ЛНДУ y ‘ — 2 x y 1 + x 2 = 1 + x 2 при начальном условии y ( 1 ) = 3 .

В нашем примере P ( x ) = — 2 x 1 + x 2 и Q ( x ) = x 2 + 1 . Начнем с того, что найдем общее решение ЛОДУ. После этого применим метод вариации произвольной постоянной и определим общее решение ЛНДУ. Это позволит нам найти искомое частное решение.

Общим решением соответствующего ЛОДУ y ‘ — 2 x y 1 + x 2 = 0 будет семейство функций y = C · ( x 2 + 1 ) , где С – произвольная постоянная.

Варьируем произвольную постоянную y = C ( x ) · ( x 2 + 1 ) и подставляем эту функцию в исходное уравнение:
y ‘ — 2 x y 1 + x 2 = 1 + x 2 C x · ( x 2 + 1 ‘ — 2 x · C ( x ) · ( x 2 + 1 ) 1 + x 2 = 1 + x 2 C ‘ ( x ) · ( x 2 + 1 ) + C ( x ) · 2 x — 2 x · C ( x ) = 1 + x 2 C ‘ ( x ) = 1 ,

откуда C ( x ) = ∫ d x = x + C 1 , где C 1 – произвольная постоянная.

Это значит, что y = C ( x ) · ( x 2 + 1 ) = ( x + C 1 ) · ( x 2 + 1 ) — общее решение неоднородного уравнения.

Теперь приступим к отысканию частного решения, которое будет удовлетворять начальному условию y ( 1 ) = 3 .

Так как y = ( x + C 1 ) · ( x 2 + 1 ) , то y ( 1 ) = ( 1 + C 1 ) · ( 1 2 + 1 ) = 2 · ( 1 + C 1 ) . Обратившись к начальному условию, получаем уравнение 2 · ( 1 + C 1 ) = 3 , откуда C 1 = 1 2 . Следовательно, искомое решение задачи Коши имеет вид y = x + 1 2 · ( x 2 + 1 )

Теперь рассмотрим еще один метод решения линейных неоднородных дифференциальных уравнений y ‘ + P ( x ) · y = Q ( x ) .

Еще один метод решения ЛНДУ первого порядка

Мы можем представить неизвестную функцию как произведение y = u ⋅ v , где u и v – функции аргумента x .

Мы можем подставить эту функцию в ЛНДУ первого порядка. Имеем:

y ‘ + P ( x ) · y = Q ( x ) ( u · v ) ‘ + P ( x ) · u · v = Q ( x ) u ‘ · v + u · v ‘ + P ( x ) · u · v = Q ( x ) u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x )

Если найти такое v , чтобы оно было ненулевым частным решением дифференциального уравнения v ‘ + P ( x ) · v = 0 , то u можно будет определить из уравнения с разделяющимися переменными u ‘ · v = Q ( x ) .

Рассмотрим этот алгоритм решения на предыдущем примере. Это позволит нам сосредоточиться на главном, не отвлекаясь на второстепенные детали.

Найдите общее решение линейного неоднородного дифференциального уравнения y ‘ — 2 x y 1 + x 2 = 1 + x 2 .

Пусть y = u ⋅ v , тогда
y ‘ — 2 x y x 2 + 1 = x 2 + 1 ⇔ ( u · v ) — 2 x · u · v x 2 + 1 = x 2 + 1 u ‘ · v + u · v ‘ — 2 x · u · v x 2 + 1 = x 2 + 1 u ‘ · v + u · v ‘ — 2 x · v x 2 + 1 = x 2 + 1

Находим такое v , отличное от нуля, чтобы выражение в скобках обращалось в ноль. Иными словами, находим частное решение дифференциального уравнения v ‘ — 2 x · v x 2 + 1 = 0 .
v ‘ — 2 x · v x 2 + 1 = 0 ⇔ d v d x = 2 x · v x 2 + 1 ⇒ d v v = 2 x d x x 2 + 1 ⇔ d v v = d ( x 2 + 1 ) x 2 + 1 ∫ d v v = ∫ d ( x 2 + 1 ) x 2 + 1 ln v + C 1 = ln ( x 2 + 1 ) + C 2

Возьмем частное решение v = x 2 + 1 , соответствующее C 2 – С 1 = 0 .

Для этого частного решения имеем
u ‘ · v + u · v ‘ — 2 x · v x 2 + 1 = x 2 + 1 ⇔ u ‘ · ( x 2 + 1 ) + u · 0 = x 2 + 1 ⇔ u ‘ = 1 ⇔ u = x + C

Следовательно, общее решение исходного линейного неоднородного дифференциального уравнения есть y = u · v = ( x + C ) · ( x 2 + 1 )

Ответы в обоих случаях совпадают. Это значит, что оба метода решения, которые мы привели в статье, равнозначны. Выбирать, какой из них применить для решения задачи, вам.

Линейные дифференциальные уравнения в высшей математике

Содержание:

Линейные дифференциальные уравнения. Линейные дифференциальные уравнения первого порядка

В предыдущей лекции мы изучали дифференциальные уравнения с разделяющимися переменными. Другим часто встречающимся типом являются линейные дифференциальные уравнения.

Определение 1. Дифференциальное уравнение вида

(1)

называется линейным дифференциальным уравнением первого порядка. Если , то линейное дифференциальное уравнение (ЛДФУ) (1) можно представить в виде:

, (2)

где .

(3)

называется линейным однородным уравнением, соответствующим уравнению (2).

Уравнение (2) — это уравнение с разделяющимися переменными. Действительно

.

Интегрируя это уравнение, получим

где — произвольная первообразная для функции , а положительная постоянная. Из последнего уравнения находим общее решение уравнение (3):

,

где — постоянная произвольного знака.

Одним из наиболее удобных методов решения уравнения (2) является метод подстановки .

Применим этот метод к уравнению (2). Получим

Приравняем выражение в квадратных скобках к нулю и найдем одно из решений этого дифференциального уравнения. Тогда линейное дифференциальное уравнение (2) будет сведено к системе двух дифференциальных уравнений с разделяющимися переменными

Найдя из системы (4) функции и , запишем общее решение уравнения (2) как .

Пример №122

.

Решение:

Данное уравнение — это ЛДФУ первого порядка (2). Применим метод подстановки .

Составим систему (4):

Решим первое уравнение системы:

Так как нам нужно одно ЧР ДФУ, то возьмем = 1. Имеем

Решаем второе уравнение:

Итак, OP Л ДФУ будет таким:

.

Убедимся проверкой в правильности решения:

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Рассмотрим линейное дифференциальное уравнение (ЛДФУ) второго порядка с постоянными коэффициентами

(5)

где — некоторые константы.

Уравнению (5) соответствует однородное ЛДФУ:

. (6)

Пусть — ОР неоднородного уравнения (5), — ЧР неоднородного уравнения (5), — ОР однородного уравнения (6). Имеет место следующее утверждение.

Теорема 1. Общее решение неоднородного уравнения (5) есть сумма общего решения соответствующего ему однородного уравнения (6) и частного решения неоднородного уравнения (5):

(7)

Рассмотрим однородное ЛДФУ (6). Имеет место следующий результат.

Теорема 2. Пусть — решения уравнения (6), тогда их линейная комбинация , где — произвольные константы, также является решением уравнения (6).

Ранее мы отмечали, что ОР ДФУ 2-го порядка зависит от двух произвольных констант. Из теоремы 2 следует, что функция

(8)

является решением уравнения (6). Возникает вопрос: может ли формула (8) определять ОР ДФУ (6). Если да, то при каких условиях? Чтобы разобраться в этом, введем несколько понятий, аналогичных сведениям из линейной алгебры.

Определение 2. Функции называются линейно независимыми, если их линейная комбинация обращается в ноль, т.е.

,

только лишь в случае . В противном случае они называются линейно зависимыми.

Определение 3. Систему функций , состоящую из двух линейно независимых решений уравнения (6), будем называть фундаментальным набором решений этого уравнения.

Имеет место следующий факт.

Теорема 3. Пусть — фундаментальный набор решений уравнения (6), тогда ОР этого уравнения задается формулой:

(9)

Фундаментальный набор решений уравнения (6) находят методом Эйлера в виде функций . Получаем . Подставляя выражения для , и в уравнение (6), имеем

.

Так как , то это соотношение эквивалентно уравнению

. (10)

Определение 4. Алгебраическое уравнение (10) называется характеристическим уравнением однородного ЛДФУ (6).

При решении характеристического уравнения могут возникать три случая.

Случай 1. Дискриминант характеристического уравнения (10) больше нуля. Тогда существует два действительных и различных решения и кратности 1. Соответствующие им решения , образуют фундаментальный набор и ОР уравнения (6) имеет вид

.

Пример №123

.

Решение:

Корнями характеристического уравнения

являются числа = 1 и =-2. Следовательно, ОР однородного ЛДФУ имеет вид

.

Проверкой можно убедиться в правильности решения.

Случай 2. Дискриминант = 0. У характеристического уравнения существует единственный действительный корень кратности 2. Ему соответствует решение . Вторым решением из фундаментального набора будет функция .

Таким образом, ОР имеет вид

.

Пример №124

.

Решение:

имеет единственный действительный корень = -3 кратности 2. Поэтому ОР имеет вид

.

Проверкой можно убедиться в правильности решения.

Случай 3. Дискриминант

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.