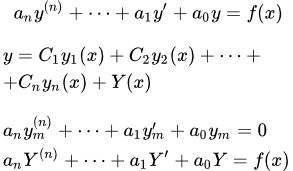Линейные однородные и неоднородные уравнения 2 порядка

Линейные однородные дифференциальные уравнения и линейные неоднородные дифференциальные уравнения 2-го порядка

Линейные однородные дифференциальные уравнения (ЛОДУ) и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка .

Частным случаем дифференциальных уравнений (ДУ) такого типа называют линейные однородные дифференциальные уравнения и линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.

Общее решение линейного однородного дифференциального уравнения на отрезке [a;b] представляет собой линейную комбинацию 2х линейно независимых частных решений y₁ и y₂ нашего уравнения, т.е.:

.

Самое сложное заключается в определении линейно независимых частных решений ДУ такого типа. Зачастую, частные решения выбирают из таких систем линейно независимых функций:

Но достаточно редко частные решения представляются именно так.

Примером линейного однородного дифференциального уравнения можно назвать .

Общее решение линейного неоднородного дифференциального уравнения определяется как ,

где y₀ является общим решением соответствующего линейного однородного дифференциального уравнения,

а является частным решением исходного ДУ. Метод определения y₀ мы сейчас обсудили, а вычисляют, используя метод вариации произвольных постоянных.

Как пример линейного неоднородного дифференциального уравнения приводим .

Познакомиться ближе с теорией и просмотреть примеры решений можете здесь: Линейные дифференциальные уравнения второго порядка.

Линейные однородные и неоднородные уравнения 2 порядка

Линейным называется дифференциальное уравнение n -го порядка , если оно 1-ой степени относительно искомой функции y ( x ) и ее производных , то есть имеет вид:

Если коэффициент P ₀ ( x ) ≠ 1, то на него можно поделить и после соответствующих переобозначений получить:

Уравнение (8.43) называется уравнением с переменными коэффициентами. Предположим, что в нем функции , непрерывны на интервале . Тогда для уравнения (8.43) на данном интервале имеет место задача Коши, сформулированная нами ранее.

Примечание. Частным случаем (8.43) является линейное дифференциальное уравнение 2-го порядка с переменными коэффициентами:

Если в уравнении (8.43) f ( x ) ≡ 0, то оно называется однородным, если f ( x ) ≠ 0, то неоднородным.

Теорема 8.3 (о структуре общего решения линейного неоднородного ДУ). Общее решение линейного неоднородного дифференциального уравнения представляет собой сумму общего решения соответствующего однородного и некоторого частного решения неоднородного уравнения . Запишем коротко:

Однородное дифференциальное уравнение, соответствующее неоднородному уравнению (8.43), имеет вид:

Пусть в уравнении (8.45) функции . Тогда оно принимает вид:

и называется линейным однородным дифференциальным уравнением n -го порядка с постоянными коэффициентами , где – функции, n раз дифференцируемые.

Рассмотрим решения уравнений (8.45) и (8.46). Обозначим полную совокупность их линейно независимых решений через . Тогда, по свойству решений однородного уравнения, их линейная комбинация также является решением уравнения (8.45) и (8.46), т о есть общее решение может быть записано в виде:

где c_i – константы интегрирования.

Перейдем к конструированию функций . Какого они вида? Так как эти функции в уравнениях (8.45) и (8.46) n раз дифференцируемы, то их конструкция при дифференцировании не меняется. Это возможно в случае экспоненциального вида функций, то есть при

где , . Отсюда, линейная комбинация функций (8.48):

– также решение уравнений (8.45) и (8.46).

Рассмотрим одну из функций (8.48) – функцию y = e λx как решение для уравнения (8.46) с постоянными коэффициентами. Продифференцируем ее n раз:

Так как e λx ≠ 0 , то ( 8.50)

–алгебраическое уравнение n -ой степени относительно λ, называемое характеристическим уравнением для уравнения (8.46). Известно, что уравнение n -ой степени имеет равно n корней как действительных, так и комплексных, с учетом их кратности. Значит, характеристическое уравнение (8.50) дает нам n значений числа λ, ранее обозначенных нами через , которые при подстановке в (8.49) приводит нас к окончательному виду общего решения линейного однородного дифференциального уравнения (8.46) с постоянными коэффициентами.

Рассмотрим наиболее распространенный частный случай уравнения (8.46) – его аналог 2-го порядка:

Для данного уравнения характеристическое уравнение (8.50) принимает вид:

Уравнение (8.52) является квадратным относительно λ. В зависимости от дискриминанта D характеристического уравнения рассматривают три случая, приведенных в таблице 8.1.

Пример 8.17. Найти общее решение уравнений:

а) Составляем характеристическое уравнение λ 2 +2 λ – 15 = 0. Корнями этого уравнения будут λ ₁ = –5 и λ ₂ = 3 . Тогда, применяя (8.53), получаем общее решение: y=C ₁ e – 5x +C ₂ e 3x .

б) Составляем характеристическое уравнение λ 2 – 16 λ + 64 = 0.

Решая это уравнение, получим λ ₁ = λ ₂ = 8 . Так как корни равные, то, применяя (8.54), будем иметь:

в) Характеристическое уравнение λ 2 – 4 λ + 13 = 0 имеет комплексные корни λ ₁ = 2+3 i и λ ₂ = 2 –3 i . Положив в (8.55) α=2 и β = 3, получим общее решение: .

г) Характеристическое уравнение λ 2 +9 = 0 имеет корни λ 1;2 = ± 3 i . П олагая в (8.55) α=0 и β = 3, получим общее решение

Рассмотрим теперь линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

Теорема 8.4. Пусть задано линейное дифференциальное неоднородное уравнение второго порядка с постоянными коэффициентами и п равой частью специального вида

1. Если не является корнем характеристического уравнения соответствующего однородного уравнения, то частное решение уравнения (8.57) имеет вид:

где – многочлены общего вида (с неопределенными коэффициентами).

2. Если – корень характеристического уравнения кратности s , то частное решение уравнения (8.57) имеет вид:

– многочлены общего вида

Рассмотрим в таблице 8.2 некоторые случаи составления частного решения линейного неоднородного дифференциального уравнения (8.57) по специальному виду его правой части.

Пример 8.18. Найти общее решение уравнения .

Решение. Найдем общее решение соответствующего однородного ДУ: . Х арактеристическое уравнение λ 2 +2 λ +1 = 0 имеет корень λ₁ = 1 кратности 2 (смотри таблицу 8.1). Значит, y_{o . o .} = c ₁ ∙ e x + c ₂ ∙ x ∙ e x . Находим частное решение исходного уравнения. В нем правая часть x –4=( x –4)∙ e 0∙ x есть формула вида P ₁ ( x )∙ e 0∙ x , причем α= 0 не является корнем характеристического уравнения: α ≠ λ . Поэтому согласно формуле (8.58), частное решение y _ч.н. ищем в виде y _ч.н. = Q ₁ ( x )∙ e 0∙ x , т.е. y _ч.н. = Ax + B , где A и B – неопределенные коэффициенты. Тогда

Пример 8.19. Решить уравнение .

уравнения . Характеристическое уравнение λ 2 – 4 λ +13 = 0 имеет корни λ₁ = 2+3 i , λ 2 = 2 –3 i (смотри таблицу 8.1). Следовательно, .

Находим частное решение y _ч.н. . Правая часть неоднородного уравнения в нашем случае имеет вид

Отсюда, сравнивая коэффициенты при косинусе и синусе, имеем . Следовательно, A = 1, B = – 3 . Поэтому . И наконец, с учетом теоремы 8.3 получаем общее решение заданного линейного неоднородного ДУ в виде:

Пример 8.20. Найти частное решение уравнения , удовлетворяющее начальным условиям .

Решение . Находим общее решение однородного уравнения . Характеристическое уравнение λ 2 – λ – 2 = 0 имеет два корня λ ₁ = –1 и λ ₂ = 2 (смотри таблицу 8.1) ; тогда y_{o . o .} = C ₁ ∙ e – x + C ₂ ∙ e 2 x – общее решение соответствующего однородного ДУ.

В правой части заданного уравнения имеется показательная функция. Так как в данном случае α=2 совпадает с одним из корней характеристического уравнения, то частное решение следует искать в виде функции Axe 2 x . Таким образом, y _ч.н. = Axe 2 x . Дифференцируя дважды это равенство, по лучим: . Подставим y _ч.н. и ее производные в левую часть заданного уравнения и найдем коэффициент A : . Следовательно, частное решение y _ч.н. = 3xe 2 x , общее решение

Используя начальные условия, определим значения произвольных постоянных C ₁ и C ₂ . Дифференцируя общее решение (8.60), получим:

Подставим в общее решение (8.60) значения x = 0 и y = 2, будем иметь 2 = C ₁ + C ₂ . Подставим в выражение для значения x = 0 и , будем иметь: 13 = – C 1 +2 C 2 +3 ; 10 = – C 1 + C 2 . Из этих уравнений составим систему , из которой находим: C 1 = – 2 и C 2 =4 . Таким образом, есть то частное решение, которое удовлетворяет заданным начальным условиям

Теорема 8.5 (о наложении решений). Если правая часть уравнения (8.56) представляет собой сумму двух функций: , а y _{1 ч.н.} и y _{2 ч.н.} – частные решения уравнений и соответственно, то функция

является частным решением данного уравнения

Линейные дифференциальные уравнения с постоянными коэффициентами

Определения

Линейное дифференциальное уравнение с постоянными коэффициентами – это уравнение, линейное относительно зависимой переменной y и ее производных:
(1) .
Член f ( x ) называется неоднородной частью уравнения.

Линейное однородное дифференциальное уравнение с постоянными коэффициентами – это уравнение вида (1), неоднородная часть которого равна нулю:
.

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами – это уравнение вида (1) с отличной от нуля неоднородной частью:
.

Здесь все коэффициенты a _i – постоянные. n – порядок уравнения.

Свойства решений линейных дифференциальных уравнений с постоянными коэффициентами

Однородные уравнения

Рассмотрим линейное однородное дифференциальное уравнение:
(2) .
Общее решение такого уравнения можно записать в виде:
,
где – линейно независимые частные решения уравнения (2). Каждое из них удовлетворят уравнению (2):
.
В этом случае говорят, что функции образуют фундаментальную систему решений линейного однородного уравнения (2).

Фундаментальная система решений линейного однородного уравнения (2) – это n линейно независимых функций , каждая из которых является решением этого уравнения.

Линейно независимые функции – это такие функции, для которых соотношение

может выполняться только если все постоянные равны нулю.

Линейно зависимые функции – это функции, между которыми имеет место линейная зависимость:
,
где – постоянные, из которых хотя бы одна отлична от нуля.

Неоднородные уравнения

Рассмотрим линейное неоднородное дифференциальное уравнение:
(3) .
Пусть Y – частное решение этого уравнения. Тогда общее решение уравнения (3) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:
.
Здесь – общее решение однородного уравнения:
;
Y – частное (любое) решение неоднородного уравнения:
.

Часто встречается случай, когда неоднородная часть может быть представлена в виде суммы функций:
.
Тогда частное решение Y также может быть представлено в виде суммы частных решений:
,
каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций :
.
В некоторых случаях бывает легче решать отдельные частные решения от более простых неоднородных частей, а затем получать частное решение для всего уравнения, суммированием полученных частных решений.

Автор: Олег Одинцов . Опубликовано: 20-07-2013 Изменено: 13-12-2019