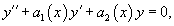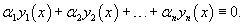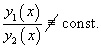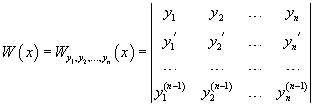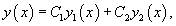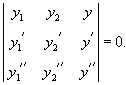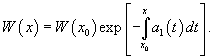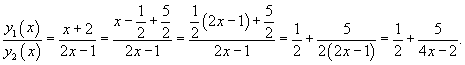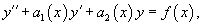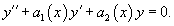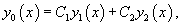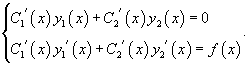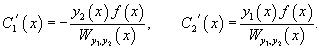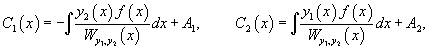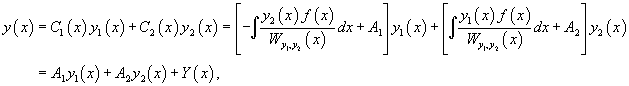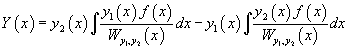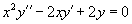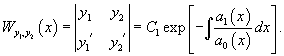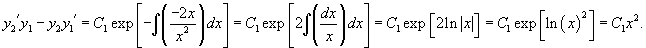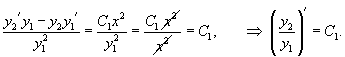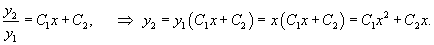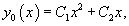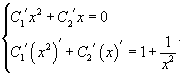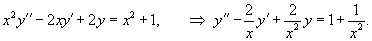Линейные однородные уравнения определитель вронского

Определитель Вронского (вронскиан).

Пусть функции $y_1(x),\;y_2(x),\;y_3(x),\ldots,y_n(x)$ непрерывны вместе с своими производными (до $n-1$ порядка включительно) на интервале $(a;b)$. Определитель Вронского (вронскиан) указанной системы функций задаётся следующей формулой:

Для того, чтобы функции $y_1(x),\;y_2(x),\;y_3(x),\ldots,y_n(x)$ были линейно независимыми на $(a;b)$, достаточно, чтобы $W(y_1,y_2,\ldots,y_n)\neq 0$ хотя бы в одной точке интервала $(a;b)$. Отметим, что это условие является достаточным, но не необходимым. Т.е. если $W(y_1,y_2,\ldots,y_n)= 0$ для всех значений переменной из интервала $(a;b)$, то про линейную зависимость функций $y_1(x),\;y_2(x),\;y_3(x),\ldots,y_n(x)$ в общем случае ничего определённого сказать нельзя.

В некоторых случаях, однако, условие $W(y_1,y_2,\ldots,y_n)\neq 0$ является не только необходимым, но и достаточным для линейной независимости функций. Например, чтобы решения $y_1(x),\;y_2(x),\;y_3(x),\ldots,y_n(x)$ линейного однородного дифференциального уравнения n-го порядка были линейно независимы на $(a;b)$, необходимо и достаточно, чтобы $W(y_1,y_2,\ldots,y_n)\neq 0$ хотя бы в одной точке интервала $(a;b)$. Об этом будет идти речь в соответствующих разделах теории дифференциальных уравнений.

Если функции $y_1(x),\;y_2(x),\;y_3(x),\ldots,y_n(x)$, непрерывные вместе с своими производными до $n-1$ порядка включительно на интервале $(a;b)$, линейно зависимы, то $W(y_1,y_2,\ldots,y_n) = 0$ для всех $x\in(a;b)$.

Исследовать на линейную зависимость функции $y_1(x)=x$, $y_2(x)=x e^x$ в их области определения.

Областью определения данных функций есть вся числовая прямая, т.е. $x\in(-\infty;+\infty)$.

Так как существует хотя бы одно значение $x\in R$, при котором $W\neq 0$ (например, при $x=1$ имеем $W=e$), то функции $y_1(x)=x$ и $y_2(x)=x e^x$ линейно независимы на $R$.

Исследовать на линейную зависимость функции $y_1(x)=1$, $y_2(x)=x$, $y_3(x)=x^2$, $y_4(x)=x^3$, $y_5(x)=x^4$ в их области определения.

Эта система функций уже была исследована в задаче №3 непосредственным применением определения линейно зависимых и независимых функций. Теперь осуществим исследование с помощью определителя Вронского. Все рассуждения проводим в области определения данных функций, т.е. на $R$.

Так как $W\neq 0$, то данные функции линейно независимы на $R$.

Исследовать на линейную зависимость функции $y_1(x)=4$, $y_2(x)=\arcsin x$, $y_3(x)=\arccos x$ в интервале $(-1;1)$.

Для вычисления полученного определителя можно использовать формулу треугольников, но лучше сделать пару предварительных преобразований. Прибавим к элементам второго столбца соответствующие элементы третьего столбца и учтем, что $\arcsin x+\arccos x=\frac <\pi><2>$ при любом $x\in[-1;1]$:

Так как $W=0$, то ничего определенного про линейную зависимость данных функций сказать нельзя.

Можно исследовать данные функции определителем Грама, но проще использовать определение линейно зависимых функций. В задаче №4 доказано по определению, что данные функции линейно зависимы на отрезке $[-1;1]$, а следовательно, будут линейно зависимы на $(-1;1)$.

Исследовать на линейную зависимость функции $y_1(x)=x$, $y_2(x)=|x|$ в их области определения.

Областью определения заданных функций есть все множество действительных чисел, т.е. $x\in R$. Рассмотрим определитель Вронского этих функций при $x≥ 0$. При данном условии $y_2(x)=|x|=x$.

Итак, вронскиан равен нулю на всей области определения заданных функций. Вновь, как и в примере №3, сказать что-либо определённое по поводу линейной зависимости функций, опираясь на значение вронскиана, нельзя. В задаче №5 эти функции были исследованы на линейную зависимость согласно определению. И, согласно результатам, функции оказались линейно независимыми.

Как видите, примеры №3 и №4 наглядно иллюстрируют тот факт, что условие $W(y_1,y_2,\ldots,y_n)\neq 0$ является достаточным, но не необходимым для линейной независимости рассматриваемых функций. В примере №3 функции были линейно зависимы, в примере №4 – линейно независимы, однако в обоих случаях $W=0$.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Линейные однородные уравнения определитель вронского

Если же это тождество выполняется лишь при , то указанные функции , , . называются линейно независимыми на отрезке .

Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функции , будут линейно независимыми на отрезке , если их отношение на данном отрезке тождественно не равно постоянной:

В противном случае, при 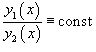, эти функции будут линейно зависимыми .

Пусть n функций , , . имеют производные порядка. Определитель

называется определителем Вронского или вронскианом для указанной системы функций.

Теорема . Если система функций , , . линейна зависима на отрезке , то ее определитель Вронского тождественно равен нулю на этом отрезке.

Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка , то функции , , . будут линейно независимыми. Это свойство определителя Вронского позволяет выяснить, являются ли найденные решения однородного дифференциального уравнения линейно независимыми.

Совокупность двух линейно независимых частных решений линейного однородного дифференциального уравнения второго порядка образует его фундаментальную систему решений .

Если , − фундаментальная система решений, то общее решение уравнения второго порядка представляется в виде

где , − произвольные постоянные.

Заметим, что по заданной фундаментальной системе решений , можно построить соответствующее однородное дифференциальное уравнение. Для случая второго порядка такое уравнение выражается через определитель в виде:

Итак, как указано выше, общее решение однородного дифференциального уравнения второго порядка является линейной комбинацией двух линейно независимых частных решений , этого уравнения.

Очевидно, что частные решения зависят от коэффициентов дифференциального уравнения. Формула Лиувилля-Остроградского устанавливает связь между вронскианом , построенном на базе частных решений , , и коэффициентом в дифференциальном уравнении.

Пусть − определитель Вронского решений , линейного однородного дифференциального уравнения 2-го порядка

К сожалению, общего метода отыскания частного решения не существует. Обычно это можно сделать путем подбора.

Если известно частное решение линейного однородного уравнения второго порядка, то его можно преобразовать к линейному уравнению первого порядка с помощью подстановки и последующей замены .

Другой способ понижения порядка основан на использовании формулы Лиувилля-Остроградского. Здесь также одно частное решение должно быть известно. Соответствующие примеры разобраны ниже.

где , и − непрерывные функции на отрезке .

Соответствующее однородное уравнение записывается в виде

Метод вариации постоянных (или метод Лагранжа) используется для построения общего решения неоднородного уравнения, когда известно общее решение ассоциированного с ним однородного уравнения.

Пусть общее решение однородного уравнения 2-го порядка выражается через фундаментальную систему решений и :

где C₁, C₂ − произвольные постоянные. Идея данного метода состоит в том, что вместо постоянных C₁ и C₂рассматриваются функции и , которые подбираются таким образом, чтобы решение удовлетворяло неоднородному уравнению.

Производные неизвестных функций и можно определить из системы уравнений

Применяя метод вариации параметров, важно помнить, что функция должна соответствовать дифференциальному уравнению, приведенному к стандартному виду, т.е. коэффициент перед старшей производной должен быть равен 1.

Далее, зная производные и , можно найти и сами функции и :

Тогда общее решение исходного неоднородного уравнения будет выражаться формулой

Теперь воспользуемся методом вариации постоянных и построим общее решение неоднородного уравнения. Будем рассматривать параметры C₁ и C₂ как функции от переменной x. Производные этих функций определяются из системы уравнений

В результате получаем общее решение неоднородного уравнения в виде

Линейная независимость функций. Определители Вронского и Грама

Пусть имеем конечную систему из функций , определенных на интервале . Функции называют линейно зависимыми на интервале , если существуют постоянные , не все равные нулю, такие, что для всех значений из этого интервала справедливо тождество

Если же это тождество выполняется только при , то функции называют линейно независимыми на интервале .

Пример 1. Показать, что система функций линейно независима на интервале .

Решение. В самом деле, равенство может выполняться для всех только при условии, что . Если же хоть одно из этих чисел не равно нулю, то в левой части равенства будем иметь многочлен степени не выше третьей, а он может обратиться в ноль не более, чем при трех значениях из данного интервала.

Пример 2. Показать, что система функций , где попарно различны, линейно независима на интервале .

Решение. Предположим обратное, т. е. что данная система функций линейно зависима на этом интервале. Тогда

на интервале , причем, по крайней мере, одно из чисел отлично от нуля, например . Деля обе части тождества (1) на , будем иметь

Дифференцируя тождество, получаем

Делим обе части тождества (2) на :

Дифференцируя (3), получаем , что невозможно, так как по предположению, по условию, а .

Наше предположение о линейной зависимости данной системы функций привело к противоречию, следовательно, эта система функций линейно независима на интервале , т.е. тождество (1) будет выполняться только при .

Пример 3. Показать, что система функций , где , линейно независима на интервале .

Решение. Определим значения и , при которых будет выполняться тождество

Разделим обе его части на :

Подставляя в (5) значение , получаем и, значит, ; но функция не равна тождественно нулю, поэтому . Тождество (5) и, следовательно, (4) имеют место только при , т. е. данные функции линейно независимы в интервале .

Замечание. Попутно доказана линейная независимость тригонометрических функций .

Пример 4. Доказать, что функции

линейно зависимы в интервале .

Решение. Покажем, что существуют такие числа , не все равные нулю, что в интервале справедливо тождество

Предполагаем тождество (7) выполненным; положим, например, . Тогда получим однородную систему трех уравнений с тремя неизвестными

Определитель этой системы трёх уравнений с тремя неизвестными равен нулю:

Следовательно, однородная система (8) имеет ненулевые решения, т. е. существуют числа , среди которых имеется по крайней мере одно отличное от нуля. Для нахождения такой тройки чисел возьмем, например, два первых уравнения системы (8):

Из первого уравнения имеем , из второго . Полагая , получим ненулевое решение системы (8):

Покажем теперь, что при этих значениях тождество (7) будет выполняться для всех . Имеем

каково бы ни было . Следовательно, система функций (6) линейно зависима на интервале .

Замечание. Для случая двух функций можно дать более простой критерий линейной независимости. Именно, функции и будут линейно независимыми на интервале , если их отношение не равно тождественной постоянной на этом интервале; если же , то функции будут линейно зависимыми.

Пример 5. Функции и линейно независимы в интервале , так как их отношение в этом интервале.

Пример 6. Функции и линейно зависимы в интервале , так как их отношение в этом интервале (в точках разрыва функции доопределяем это отношение по непрерывности).

Пусть функций имеют производные (n–1)-го порядка. Определитель

называется определителем Вронского для этой системы функций. Определитель Вронского вообще является функцией от , определенной в некотором интервале.

Пример 7. Найти определитель Вронского для функций .

Пример 8. Найти определитель Вронского для функций:

так как первая и последняя строки определителя пропорциональны.

Теорема. Если система функций линейно зависима на отрезке , то ее определитель Вронского тождественно равен нулю на этом отрезке.

Так, например, система функций линейно зависима в интервале , и определитель Вронского этих функций равен нулю всюду в этом интервале (см. примеры 4 и 8).

Эта теорема дает необходимое условие линейной зависимости системы функций. Обратное утверждение неверно, т. е. определитель Вронского может тождественно обращаться в ноль и в том случае, когда данные функции образуют линейно независимую систему на некотором интервале.

Пример 9. Рассмотрим две функции:

Графики их имеют вид, указанный на рис. 25.

Эта система функций линейно независима, так как тождество выполняется только при . В самом деле, рассматривая его на отрезке , мы получаем , откуда , так как ; на отрезке же имеем , откуда , так как на этом отрезке.

Найдем определитель Вронского системы. На отрезках и :

Таким образом, определитель Вронского на отрезке тождественно равен нулю.

Пусть имеем систему функций на отрезке . Положим

называется определителем Грама системы функций .

Теорема. Для того, чтобы система функций была линейно зависимой, необходимо и достаточно, чтобы ее определитель Грама равнялся нулю.

Пример 10. Показать, что функции и линейно зависимы на отрезке .

Вычислим определитель Грама следовательно, функции и линейно зависимы.