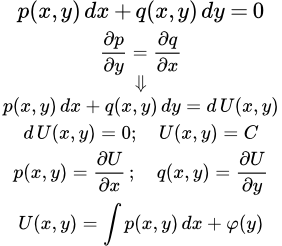Линейные однородные уравнения в полных дифференциальных уравнениях

Дифференциальные уравнения в полных дифференциалах

Введение

Если найдена такая функция U ( x, y ) , то уравнение принимает вид:
dU ( x, y ) = 0 .
Его общий интеграл:
U ( x, y ) = C ,
где C – постоянная.

Если дифференциальное уравнение первого порядка записано через производную:
,
то его легко привести к форме (1). Для этого умножим уравнение на dx . Тогда . В результате получаем уравнение, выраженное через дифференциалы:
(1) .

Свойство дифференциального уравнения в полных дифференциалах

Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:
(2) .

Доказательство

Далее мы полагаем, что все функции, используемые в доказательстве, определены и имеют соответствующие производные в некоторой области значений переменных x и y . Точка x ₀ , y ₀ также принадлежит этой области.

Докажем необходимость условия (2).
Пусть левая часть уравнения (1) является дифференциалом некоторой функции U ( x, y ) :
.
Тогда
;
.
Поскольку вторая производная не зависит от порядка дифференцирования, то
;
.
Отсюда следует, что . Необходимость условия (2) доказана.

Докажем достаточность условия (2).
Пусть выполняется условие (2):
(2) .
Покажем, что можно найти такую функцию U ( x, y ) , что ее дифференциал:
.
Это означает, что существует такая функция U ( x, y ) , которая удовлетворяет уравнениям:
(3) ;
(4) .
Найдем такую функцию. Проинтегрируем уравнение (3) по x от x ₀ до x , считая что y – это постоянная:
;
;
(5) .
Дифференцируем по y считая, что x – это постоянная и применим (2):

.
Уравнение (4) будет выполнено, если
.
Интегрируем по y от y ₀ до y :
;
;
.
Подставляем в (5):
(6) .
Итак, мы нашли функцию, дифференциал которой
.
Достаточность доказана.

В формуле (6), U ( x ₀ , y ₀) является постоянной – значением функции U ( x, y ) в точке x ₀ , y ₀ . Ей можно присвоить любое значение.

Как распознать дифференциальное уравнение в полных дифференциалах

Рассмотрим дифференциальное уравнение:
(1) .
Чтобы определить, является ли это уравнение в полных дифференциалах, нужно проверить выполнение условия (2):
(2) .
Если оно выполняется, то это уравнение в полных дифференциалах. Если нет – то это не уравнение в полных дифференциалах.

Пример

Проверить, является ли уравнение в полных дифференциалах:
.

Здесь
, .
Дифференцируем по y , считая x постоянной:

.
Дифференцируем по x , считая y постоянной:

.
Поскольку:
,
то заданное уравнение – в полных дифференциалах.

Методы решения дифференциальных уравнений в полных дифференциалах

Метод последовательного выделения дифференциала

Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:
du ± dv = d ( u ± v ) ;
v du + u dv = d ( uv ) ;
;
.
В этих формулах u и v – произвольные выражения, составленные из любых комбинаций переменных.

Пример 1

Ранее мы нашли, что это уравнение – в полных дифференциалах. Преобразуем его:
(П1) .
Решаем уравнение, последовательно выделяя дифференциал.
;
;
;
;

.
Подставляем в (П1):
;
.

Метод последовательного интегрирования

В этом методе мы ищем функцию U ( x, y ) , удовлетворяющую уравнениям:
(3) ;
(4) .

Проинтегрируем уравнение (3) по x , считая y постоянной:
.
Здесь φ ( y ) – произвольная функция от y , которую нужно определить. Она является постоянной интегрирования. Подставляем в уравнение (4):
.
Отсюда:
.
Интегрируя, находим φ ( y ) и, тем самым, U ( x, y ) .

Пример 2

Решить уравнение в полных дифференциалах:
.

Ранее мы нашли, что это уравнение – в полных дифференциалах. Введем обозначения:
, .
Ищем Функцию U ( x, y ) , дифференциал которой является левой частью уравнения:
.
Тогда:
(3) ;
(4) .
Проинтегрируем уравнение (3) по x , считая y постоянной:
(П2)
.
Дифференцируем по y :

.
Подставим в (4):
;
.
Интегрируем:
.
Подставим в (П2):

.
Общий интеграл уравнения:
U ( x, y ) = const .
Объединяем две постоянные в одну.

Метод интегрирования вдоль кривой

Функцию U , определяемую соотношением:
dU = p ( x, y ) dx + q ( x, y ) dy ,
можно найти, если проинтегрировать это уравнение вдоль кривой, соединяющей точки ( x ₀ , y ₀) и ( x, y ) :
(7) .
Поскольку
(8) ,
то интеграл зависит только от координат начальной ( x ₀ , y ₀) и конечной ( x, y ) точек и не зависит от формы кривой. Из (7) и (8) находим:
(9) .
Здесь x ₀ и y ₀ – постоянные. Поэтому U ( x ₀ , y ₀) – также постоянная.

Пример такого определения U был получен при доказательстве свойства уравнения в полных дифференциалах:
(6) .
Здесь интегрирование производится сначала по отрезку, параллельному оси y , от точки ( x ₀ , y ₀ ) до точки ( x ₀ , y ) . Затем интегрирование производится по отрезку, параллельному оси x , от точки ( x ₀ , y ) до точки ( x, y ) .

В более общем случае, нужно представить уравнение кривой, соединяющей точки ( x ₀ , y ₀ ) и ( x, y ) в параметрическом виде:
x ₁ = s ( t ₁) ; y ₁ = r ( t ₁) ;
x ₀ = s ( t ₀) ; y ₀ = r ( t ₀) ;
x = s ( t ) ; y = r ( t ) ;
и интегрировать по t ₁ от t ₀ до t .

Наиболее просто выполняется интегрирование по отрезку, соединяющим точки ( x ₀ , y ₀ ) и ( x, y ) . В этом случае:
x ₁ = x ₀ + ( x – x ₀) t ₁ ; y ₁ = y ₀ + ( y – y ₀) t ₁ ;
t ₀ = 0 ; t = 1 ;
dx ₁ = ( x – x ₀) dt ₁ ; dy ₁ = ( y – y ₀) dt ₁ .
После подстановки, получается интеграл по t от 0 до 1 .
Данный способ, однако, приводит к довольно громоздким вычислениям.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 10-08-2012 Изменено: 02-07-2015

Однородные дифференциальные уравнения
и приводящиеся к ним

Однородные уравнения

Функция называется однородной функцией своих аргументов измерения , если справедливо тождество .

Например, функция есть однородная функция второго измерения, так как

При имеем функцию нулевого измерения. Например, есть однородная функция нулевого измерения, так как

Дифференциальное уравнение вида называется однородным относительно и , если есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде

Вводя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющими переменными:

Если есть корень уравнения , то решение однородного уравнения будет или (прямая, проходящая через начало координат).

Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .

Пример 1. Решить однородное уравнение .

Решение. Запишем уравнение в виде так что данное уравнение оказывается однородным относительно и . Положим , или . Тогда . Подставляя в уравнение выражения для и , получаем . Разделяем переменные: . Отсюда интегрированием находим

Так как , то, обозначая , получаем , где или . Заменяя на , будем иметь общий интеграл .

Отсюда общее решение: .

При разделении переменных мы делили обе части уравнения на произведение , поэтому могли потерять решение, которые обращают в ноль это произведение.

Положим теперь и . Но в силу подстановки , а из соотношения получаем, что , откуда . Непосредственной проверкой убеждаемся, что функции и также являются решениями данного уравнения.

Пример 2. Рассмотреть семейство интегральных кривых однородного уравнения . Показать, что касательные в соответственных точках к кривым, определяемым этим однородным дифференциальным уравнением, параллельны между собой.

Примечание: Будем называть соответственными те точки на кривых , которые лежат на одном луче, выходящем из начала координат.

Решение. По определению соответственных точек имеем , так что в силу самого уравнения , где и — угловые коэффициенты касательных к интегральным кривым и , в точках и соответственно (рис. 12).

Уравнения, приводящиеся к однородным

А. Рассмотрим дифференциальное уравнение вида

где — постоянные, а — непрерывная функция своего аргумента .

Если , то уравнение (3) является однородным и оно интегрируется, как указано выше.

Если хотя бы одно из чисел отлично от нуля, то следует различать два случая.

1) Определитель . Вводя новые переменные и по формулам , где и — пока неопределенные постоянные, приведем уравнение (3) к виду

Выбирая и как решение системы линейных уравнений

получаем однородное уравнение . Найдя его общий интеграл и заменив в нем на , a на , получаем общий интеграл уравнения (3).

2) Определитель . Система (4) в общем случае не имеет решений и изложенный выше метод неприменим; в этом случае , и, следовательно, уравнение (3) имеет вид . Подстановка приводит его к уравнению с разделяющимися переменными.

Пример 3. Решить уравнение .

Решение. Рассмотрим систему линейных алгебраических уравнений

Определитель этой системы .

Система имеет единственное решение . Делаем замену . Тогда уравнение (5) примет вид

Это уравнение является однородным уравнением. Полагая , получаем

Интегрируя, найдем или .

Возвращаемся к переменным :

Пример 4. Решить уравнение .

Решение. Система линейных алгебраических уравнений несовместна. В этом случае метод, примененный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку , . Уравнение примет вид

Разделяя переменные, получаем

Возвращаясь к переменным , получаем общий интеграл данного уравнения

Б. Иногда уравнение можно привести к однородному заменой переменного . Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному приписать измерение 1, переменному — измерение и производной — измерение .

Пример 5. Решить уравнение .

Решение. Делаем подстановку , где пока произвольное число, которое мы выберем позже. Подставляя в уравнение выражения для и , получим

Заметим, что имеет измерение имеет измерение , имеет измерение . Полученное уравнение будет однородным, если измерения всех членов одинаковы, т.е. если выполняется условие , или .

Положим ; исходное уравнение принимает вид

Положим теперь . Тогда это уравнение примет вид , откуда .

Разделяем переменные в этом уравнении . Интегрируя, найдем

Заменяя через , получаем общий интеграл данного уравнения

Уравнение имеет еще очевидное решение , которое получается из общего интеграла при , если интеграл записать в виде , а затем перейти к пределу при . Таким образом, функция является частным решением исходного уравнения.

Линейные дифференциальные уравнения высших порядков

Оговорим сразу тот факт, что нахождение решения общего аналитического вида для линейных однородных и неоднородных дифференциальных уравнений высших порядков зачастую невозможно. В основном пользуются приближенными методами решения.

Материал данной статьи представлен базовой теоретической информацией на тему решения ЛОДУ
n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 и ЛНДУ n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) .

Сначала поговорим о линейных однородных дифференциальных уравнениях n -ого порядка, а затем займемся неоднородными ДУ.

Линейные однородные дифференциальные уравнения

Общее решение для линейного однородного дифференциального уравнения n -ого порядка y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 при непрерывных на интервале интегрирования
X коэффициентах f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) определяет линейная комбинация y 0 = ∑ j = 1 n C j · y j , в которой y j , j = 1 , 2 , . . . , n являются линейно независимыми частными решениями ЛОДУ на X , а C j , j = 1 , 2 , . . . , n являются произвольными постоянными.

Когда тождество a 1 · y 1 + a 2 · y 2 + . . . + a n · y n ≡ 0 верно только при нулевых коэффициентах a 1 = a 2 = . . . = a n = 0 , функции y j , j = 1 , 2 , . . . , n являются линейно независимыми на неком интервале X .

Для линейно независимых функций y j , j = 1 , 2 , . . . , n определитель Вронского при любых
x из X отличен от нуля:

W ( x ) = y 1 y 2 … y n y ‘ 1 y ‘ 2 … y ‘ n y » 1 y » 2 … y » n … … … … y 1 ( n — 1 ) y 2 ( n — 1 ) … y n ( n — 1 ) ≠ 0

Тот факт, что определитель Вронского не равен нулю, возможно применять в качестве критерия линейной независимости функций на интервале.

Каким же образом определяются y j , j = 1 , 2 , . . . , n — линейно независимые частные решения линейного однородного дифференциального уравнения n -ого порядка?

В большинстве случаев данные функции возможно подобрать, используя стандартные системы линейно независимых функций:

1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 · x , e k 2 · x , . . . , e k n · x 3 ) e k 1 · x , x · e k 1 · x , . . . , x n 1 · e k 1 · x , e k 2 · x , x · e k 2 · x , . . . , x n 2 · e k 2 · x , . . . e k p · x , x · e k p · x , . . . , x n p · e k p · x

Когда подобраны все n линейно независимые частные решения y j , j = 1 , 2 , . . . , n , возможно составить общее решение линейного однородного дифференциального уравнения n -ого порядка y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = 0 — оно будет иметь запись y 0 = ∑ j = 1 n C j · y j . Когда подобраны только несколько линейно независимых частных решений, мы можем понизить степень заданного уравнения при помощи замены. Детально этот пункт мы не будем рассматривать, в случае необходимости следует изучить дополнительные материалы по теме.

Линейные неоднородные дифференциальные уравнения

Приступим к рассмотрению линейных неоднородных дифференциальных уравнений n -ого порядка записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) .

Общее решение на интервале X линейного неоднородного дифференциального уравнения порядка n записи y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) при непрерывных на интервале интегрирования X коэффициентах f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) и непрерывной функции f ( x ) определяется как сумма общего решения y 0 соответствующего ЛОДУ и некоторого частного решения y

заданного неоднородного уравнения: y = y 0 + y

Нахождение y 0 — общего решения соответствующего ЛОДУ n -ого порядка — было рассмотрено выше. Остается разобрать, как находится y

— частное решение линейного неоднородного дифференциального уравнения n -ого порядка.

Иногда некое частное решение y

бывает достаточно явным, то есть его возможно подобрать. Когда
y

подобрать затруднительно, при этом определены n линейно независимых частных решений y j , j = 1 , 2 , . . . , n соответствующего ЛОДУ, общее решение исходного ЛНДУ n -ого порядка возможно определить при помощи метода вариации произвольных постоянных.

В таком случае общее решение линейного неоднородного дифференциального уравнения y ( n ) + f ( n — 1 ) ( x ) · y n — 1 + . . . + f 0 ( x ) · y = f ( x ) определяется как y = ∑ j = 1 n C j ( x ) · y j , а функции C 1 ( x ) , C 2 ( x ) , … , C n ( x ) находятся интегрированием после решения системы уравнений:

∑ j = 1 n C j ‘ ( x ) · y j = 0 ∑ j = 1 n C j ‘ ( x ) · y ‘ j = 0 ∑ j = 1 n C j ‘ ( x ) · y » j = 0 … ∑ j = 1 n C j ‘ ( x ) · y j ( n — 2 ) = 0 ∑ j = 1 n C j ‘ ( x ) · y j ( n — 1 ) = 0