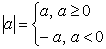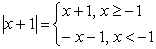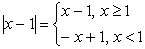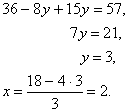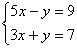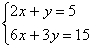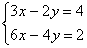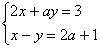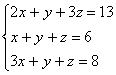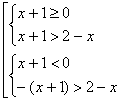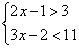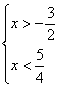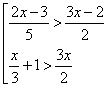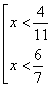Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок № 1. Повторение 7-9. Числовые и алгебраические выражения. Линейные уравнения и неравенства
Перечень вопросов, рассматриваемых в теме.
- обобщение и систематизация знаний по алгебре 7-9;
- повтор арифметики алгебраических выражений;
- решение линейных уравнений и неравенств;
- решение систем линейных уравнений и неравенств.
1. Колягин Ю. М., Ткачева М. В., Фёдорова Н. Е. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни.
2. Ткачева М. В., Федорова Н. Е. Алгебра и начала математического анализа. Тематические тесты. 10 класс. Базовый и профильный уровни
1. Шабунин М. И., Ткачева М. В., Фёдорова Н. Е. и др. Алгебра и начала математического анализа. Дидактические материалы. 10 класс. Профильный уровень.
2. Галицкий М. Л., Гольдман А. М., Звавич Л. И. Сборник задач по алгебре для 8-9 классов. Учеб. пособие для учащихся школ и классов с углубленным изучением математики. М.: Просвещение, 2000.
Открытые электронные ресурсы:
1. Федеральный институт педагогических измерений. http://www.fipi.ru
Все выражения можно разбить на два класса на основании наличия переменных: числовые выражения и выражения с переменными.
Логическая задача на классификацию
Основание для классификации: наличие переменных
Выражения с переменными
Для числовых выражений можно находить значение – результат всех выполненных действий. Для выражений с переменными можно также находить значение при некоторых значениях переменных, предварительно упростив его, например, с помощью свойств, правил, формул сокращенного умножения.
Найдите значение выражения при a=0,01 и b=12:
2) 
3) 
2)
; 
3) 
3b-2a-3b=-2a-2a=-0,02
2.Линейное уравнение с одним неизвестным
Линейное уравнение с одним неизвестным – это уравнение вида ax=b, где a и b – заданные числа, x – неизвестное
Решить уравнение – это значит найти все его корни или установить, что корней нет
Основные свойства уравнений
Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
Решение уравнения ax=b,где a и b – числа, x – переменная
Если a≠0, b – любое число, то 
.
Если a=0, b≠0, то нет корней.
Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
1) 
,
1)
,
Решим уравнение 2).
По определению модуля числа имеем 5x+7=±2.
Таким образом, либо 5x+7=2, откуда x=-1, либо 5x+7=-2, откуда x=-1,8. Получаем ответ: -1; -1,8.
Решение уравнения ax=b,где a и b – числа, x – переменная
Если a≠0, b – любое число, то 
.
Если a=0, b≠0, то нет корней.
Если a=0, b=0, то x – любое число.
Линейное уравнение с параметрами
Решите уравнение (5x+7)n=x-m, где m и n – некоторые числа, x – неизвестное
1)Если 5n-1≠0, то есть n≠0,2, то 
. Используя основное свойство дроби, получаем, что 
.
2)Если 5n-1=0, то есть n=0,2, то уравнение примет вид 0∙x=-m-1,4;
Тогда при m=-1,4 корнем уравнения будет любое число,
при m≠-1,4 уравнение не имеет корней.
Рассмотрим задачу 1.
От пристани А до пристани В катер плывет по реке 15 минут, а обратно 20 минут. Найти скорость течения реки, если собственная скорость катера 14 км/ч.
Для ее решения необходимо:
1.Провести ориентировку в тексте задачи.
1.1.Проанализировать условие и выявить данные (известные, дополнительные, скрытые).
1.2.Проанализировать вопрос задачи и выявить искомое.
1.3.Определить связи одноуровневые и межуровневые между данными и искомым.
1.4.Построить графическую схему, например, таблицу.
1.5.Установить в ней место искомого.
2.Спланировать способ решения задачи.
2.1.Подобрать метод, например, алгебраический.
2.3.Подобрать действия для решения составленной математической модели.
3.Исполнить намеченный план решения и найти искомое.
4.Провести самоконтроль решения задачи, проверив, что найденное искомое не противоречит условию задачи.
5.Провести самооценку решения задачи.
6.Провести самокоррекцию выполненного решения задачи, если есть в том необходимость.
1 способ: Провести повторное решение задачи от начала до конца.
2 способ: Провести дополнительную деятельность для того, чтобы ответить на вопрос задачи.
3 способ: Решить задачу другим способом.
удовлетворяет условию 
3.Системы линейных уравнений с двумя неизвестными
Система двух уравнений первой степени с двумя неизвестными – это система вида
где x и y – неизвестные,
– заданные числа,
причем 
и 
.
Решение системы двух уравнений с двумя неизвестными – это пара чисел x и y, которые при подстановке в эту систему обращают каждое ее уравнение в верное числовое равенство.
Решить систему уравнений – это значит найти все ее решения или установить, что их нет.
Способы решения систем уравнений: способ подстановки и способ сложения.
Решите систему способом подстановки
Для этого необходимо:
1.Выразить одну переменную через другую из какого-либо уравнения.
2.Подставить полученное выражение вместо выраженной переменной в другое уравнение.
3.Решить полученное уравнение относительно одной переменной.
4.Найти значение другой переменной, подставив найденный корень в формулу пункта 1.
5.Записать решение системы.
(1;2) – решение системы
Решите систему способом сложения
Для этого необходимо:
1.Домножить какое-либо уравнение системы или оба уравнения на такие числа, чтобы при почленном сложении уравнений получить уравнение относительно одной переменной.
2.Решить уравнение, полученное после почленного сложения.
3.Подставить найденный корень в какое-либо уравнение исходной системы.
4.Решить составленное уравнение.
5.Записать решение системы.
(3;-1) – решение системы
Решение системы двух линейных уравнений с двумя неизвестными
Если 
, то система имеет единственное решение.
Если 
то система не имеет решений.
Если 
, то система имеет бесконечно много решений.
Система линейных уравнений с параметром
Решите систему уравнений с параметром a:
Решим систему способом подстановки. Выразим y из первого уравнения системы: 
. Подставим выражение 
вместо y во второе уравнение системы:
(a-3)x+a((a+1)x-a)=-9 .
Решим полученное уравнение относительно x:
.
1. Если 
, то есть 
, то система имеет единственное решение. Найдем это решение: 
После сокращения получаем: 
. Найдем соответствующее значение y, подставив 
вместо x в формулу 
. Получим 
. Итак, если 
, то 
– решение системы.
2. Если 
и 
, то есть a=-3, то система имеет бесконечно много решений. Найдем в этом случае решения системы. Для этого подставим a=-3 в первое уравнение системы. Получим уравнение -2x-y=-3, из которого выразим y: y=3-2x. Значит, (x;3-2x), где x – любое число, — решения системы.
3. Если 
и 
, то есть a=1, то система не имеет решений.
Ответ: Если 
, то 
– решение системы;
если a=-3, то (x;3-2x), где x – любое число, — решения системы;
если a=1, то система не имеет решений.
4.Решение линейных неравенств с одним неизвестным
Неравенство первой степени с одним неизвестными – это неравенство вида ax b / ax≤b / ax ≥b, где a и b – заданные числа, x – неизвестное.
Решение неравенства с одним неизвестным – это то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство.
Решить неравенство – это значит найти все его решения или установить, что их нет.
Правило решения неравенства первой степени с одним неизвестным
1.Перенести с противоположными знаками члены, содержащие неизвестное, из правой части в левую, а не содержащие неизвестное – из левой части в правую.
2.Привести подобные члены в левой и правой частях неравенства.
3.Если коэффициент при неизвестном отличен от нуля, то разделить на него обе части неравенства.
5.Системы линейных неравенств с одним неизвестным
Решение системы неравенств с одним неизвестным – это значение неизвестного, при котором все неравенства системы обращаются в верные числовые неравенства.
Решить неравенство 2x-8 3.
Решение неравенства ax 0, то 
Если a 0, то x – любое число
Если a=0, b≤0, то решений нет
Линейное неравенство с параметром
Решите неравенство с параметром a:
ax 0, то 
Если a 0, то 
; если a 0, 2x>6, x>3.
Решим второе неравенство системы:
4x-20 b / ax≤b / ax ≥b, где a и b – заданные числа, x – неизвестное.
Система двух уравнений первой степени с двумя неизвестными – это система вида
где x и y – неизвестные,
– заданные числа,
причем 
и 
.
Урок по теме «Решение линейных уравнений и неравентсв»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Урок алгебры в 7 классе по теме : Решение линейных уравнений и неравенств.
Тип урока: закрепление и обобщения знаний
Задачи: создать условия для развития определять взаимное расположение графиков по виду линейных функций, находить компоненты линейной функции, находить решение линейного неравенства по графику заданной функции.
Предметные: обобщить и систематизировать знания учащихся о линейной функции, её свойствах, формировать навык применение свойств линейной функции при решении линейных уравнений и неравенств.
Метапредметные: познавательные – ориентироваться на разнообразие способов решения задач;
Регулятивные – учитывать правило в планировании и контроле способа решения;
Коммуникативные – учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве.
Личностные: формировать интерес к изучению темы и желанию применять приобретенные знания и умения.
Организационная структура урока
Содержание деятельности учителя
Содержание деятельности ученика (осуществляемые действия)
Формируемые способы деятельности
I . Организационный этап.
II . Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
III . Актуализация знаний учащихся.
Задает учащимся вопросы: 1) как могут располагаться прямые на плоскости (демонстрирует 1 слайд презентации);
2) как узнать по заданным уравнениям прямым как они располагаются относительно друг друга?
Выбрать из данных уравнений функций:
y=2x-3; y=-0,5x+4; y=2x+0,6; y=2(x-1,5); y=3x-8
А) параллельные прямые
Б) совпадающие прямые
В) перпендикулярные прямые
Г) пересекающиеся прямые
3) Дана функция y =1,5 x + b и точка А(4;7), лежащая на графике функции.
а) написать уравнение этой функции (найти b )
б) построить график
в) построить графики, симметричные полученному, относительно осей координат и написать их уравнения
г) указать фигуру, заключенную между графиками.
4) Сколько точек пересечения может иметь прямая с осью OX (демонстрирует слайд 2).
Отвечают на поставленные вопросы: 1)могут быть параллельными, совпадать, пересекаться и быть перпендикулярными (частный случай пресечения прямых);
2) если угловые коэффициенты прямых равны, а свободные члены нет, то прямые параллельны, если угловые коэффициенты прямых не равны, то прямые пересекаются; если произведение угловых коэффициентов равно -1, то прямые перпендикулярные, иначе прямые совпадают.
А) y =2 x -3 и y =2 x +0,6
Б) y =2 x -3 и y =2( x -1,5)
В) y =2 x -3 и y =-0,5 x +4
Г) y =3 x -8 и y =2 x -3;
y =-0,5 x +4 и y =3 x -8;
y =2 x +0,6 и y =3 x -8.
3) Выполняют письменно в тетрадях, один на закрытой доске.
Отвечают устно: одну, не иметь общих точек и бесконечно много.
Участвовать в диалоге, понимать точку зрения собеседника; подбирать аргументы для ответа на поставленный вопрос;
IV . Объяснение нового материала
Теоретический материал темы: демонстрация слайдов 3-7
V . Первичное закрепление нового материала.
Задача 1.1.4. (из практики) задайте уравнение прямой и найдите корень уравнения y ( x )=3
Задача 1.1.5. (из практики) задайте уравнение прямой и найдите корень уравнения y ( x )= — 2
Задача 1.1.6. (из практики) на рисунке изображен график функции y = y ( x ). Найдите корень уравнения y ( x )=0. Найдите множество решений неравенства y ( x )≥0, y ( x )≤0. Найдите множество решений неравенства y ( x ) ≥ -1
Пишут на готовых иллюстрациях c комментариями:
y= -3x; y=3 при x= -1
1.1.5) b=2 k= -2:2=-1 y= -x+2
1.1.6) y ( x )=0 при x =2
y ( x ) ≥0 при x є [2; +∞)
y ( x ) ≤0 при x є (-∞;2]
y ( x ) ≥-1 при x є [-1; +∞)
воспроизводить полученную информацию с заданной степенью свернутости; работать по заданному алгоритму.
Подводя итог уроку, просит учащихся продолжить высказывания об уроке:
Урок привлек меня тем….
На уроке мне было сложно…
Я бы свою работу на уроке оценил….
Заносят ответы в специальный бланк опроса
VII. Домашнее задание.
№320 дополнительно: для каждого графика решить уравнение y ( x )=0 и неравенства y ( x )≥0, y ( x )≤0.
Творческое задание из ЦОР № 1.1.7- 1.1.9, 1.1.11
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 932 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 308 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 573 258 материалов в базе
Материал подходит для УМК
«Алгебра», Никольский С.М., Потапов М.К., Решетников Н.Н. и др.
9.3. Решение линейных уравнений с одним неизвестным
Другие материалы
- 13.02.2022
- 39
- 1
- 13.02.2022
- 37
- 1
- 13.02.2022
- 31
- 0
- 13.02.2022
- 267
- 11
- 13.02.2022
- 22
- 0
- 13.02.2022
- 36
- 1
- 13.02.2022
- 41
- 0
- 13.02.2022
- 35
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 13.02.2022 43
- DOCX 17.5 кбайт
- 0 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Медко Ольга Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 7 месяцев
- Подписчики: 0
- Всего просмотров: 8930
- Всего материалов: 9
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
В Забайкалье в 2022 году обеспечат интернетом 83 школы
Время чтения: 1 минута
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
Рособрнадзор не планирует переносить досрочный период ЕГЭ
Время чтения: 0 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
«Линейные уравнения и неравенства»
Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.
Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.
Просмотр содержимого документа
«»Линейные уравнения и неравенства»»
Линейные уравнения и неравенства
Романишина Дина Соломоновна, учитель математики гимназии №2 г. Хабаровска
1. Уравнения с одной переменной.
Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.
Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.
Решить уравнение — значит найти все его корни или доказать, что корней нет.
Уравнения называются равносильными, если все корни первого уравнения являются корнями второго уравнения и наоборот, все корни второго уравнения являются корнями первого уравнения или, если оба уравнения не имеют корней. Например, уравнения х-8=2 и х+10=20 равносильны, т.к. корень первого уравнения х=10 является корнем и второго уравнения, и оба уравнения имеют по одному корню.
При решении уравнений используются следующие свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Уравнение ах=b, где х – переменная, а и b – некоторые числа, называется линейным уравнением с одной переменной.
Если а¹0, то уравнение имеет единственное решение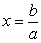 
.
Если а=0, b=0, то уравнению удовлетворяет любое значение х.
Если а=0, b¹0, то уравнение не имеет решений, т.к. 0х=b не выполняется ни при одном значении переменной.
Пример 1. Решить уравнение: -8(11-2х)+40=3(5х-4)
Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим:
Пример 2. Решить уравнения:
Эти уравнения не являются линейными, но покажем, как можно решать такие уравнения.
3х2-5х=0; х(3х-5)=0. Произведение равно нулю, если один из множителей равен нулю, получаем х1=0; х2=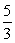
.
Ответ: 0;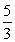 
.
Разложить на множители левую часть уравнения:
х2(х-2)-9(х-2)=(х-2)(х2-9)=(х-2)(х-3)(х-3), т.е. (х-2)(х-3)(х+3)=0. Отсюда видно, что решениями этого уравнения являются числа х1=2, х2=3, х3=-3.
с) Представим 7х, как 3х+4х, тогда имеем: х2+3х+4х+12=0, х(х+3)+4(х+3)=0, (х+3)(х+4)=0, отсюда х1=-3, х2=- 4.
Ответ: -3; — 4.
Пример 3. Решить уравнение: ½х+1ç+½х-1ç=3.
Напомним определение модуля числа: 
Например: ½3½=3, ½0½=0, ½- 4½= 4.
В данном уравнении под знаком модуля стоят числа х-1 и х+1. Если х меньше, чем –1, то число х+1 отрицательное, тогда ½х+1½=-х-1. А если х-1, то ½х+1½=х+1. При х=-1 ½х+1½=0.
Таким образом, 
Аналогично 
а) Рассмотрим данное уравнение½х+1½+½х-1½=3 при х£-1, оно равносильно уравнению -х-1-х+1=3, -2х=3, х=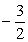
, это число принадлежит множеству х£-1.
b) Пусть -1 х £ 1, тогда данное уравнение равносильно уравнению х+1-х+1=3, 2¹3 уравнение не имеет решения на данном множестве.
с) Рассмотрим случай х1.
х+1+х-1=3, 2х=3, х=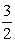
. Это число принадлежит множеству х1.
Ответ: х1=-1,5; х2=1,5.
Пример 4. Решить уравнение:½х+2½+3½х½=2½х-1½.
Покажем краткую запись решения уравнения, раскрывая знак модуля «по промежуткам».
Ответ: [-2; 0]
Пример 5. Решить уравнение: (а-1)(а+1)х=(а-1)(а+2), при всех значениях параметра а.
В этом уравнении на самом деле две переменных, но считают х–неизвестным, а а–параметром. Требуется решить уравнение относительно переменной х при любом значении параметра а.
Если а=1, то уравнение имеет вид 0×х=0, этому уравнению удовлетворяет любое число.
Если а=-1, то уравнение имеет вид 0×х=-2, этому уравнению не удовлетворяет ни одно число.
Если а¹1, а¹-1, тогда уравнение имеет единственное решение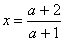 
.
Ответ: если а=1, то х – любое число;
если а=-1, то нет решений;
если а¹±1, то .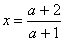
2. Системы уравнений с двумя переменными.
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему — значит найти все ее решения или доказать, что их нет. Две системы уравнений называются равносильными, если каждое решение первой системы является решением второй системы и каждое решение второй системы является решением первой системы или они обе не имеют решений.
При решении линейных систем используют метод подстановки и метод сложения.
Пример 1. Решить систему уравнений:
Для решения этой системы применим метод подстановки. Выразим из первого уравнения х и подставим это значение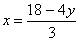 
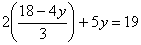
во второе уравнение системы, получим
,
Пример 2. Решить систему уравнений:
Для решения этой системы применим метод сложения уравнений. 8х=16, х=2. Подставим значение х=2 в первое уравнение, получим 10-у=9, у=1.
Пример 3. Решить систему уравнений:
Эта система равносильна одному уравнению 2х+у=5, т.к. второе уравнение получается из первого умножением на 3. Следовательно, ей удовлетворяет любая пара чисел (х; 5-2х). Система имеет бесконечное множество решений.
Ответ: (х; 5-2х), х–любое.
Пример 4. Решить систему уравнений:
Умножим первое уравнение на –2 и сложим со вторым уравнением, получим 0×х+0×у=-6. Этому уравнению не удовлетворяет ни одна пара чисел. Следовательно, эта система не имеет решений.
Ответ: система не имеет решений.
Пример 5. Решить систему:
Из второго уравнения выражаем х=у+2а+1 и подставляем это значение х в первое уравнение системы, получаем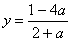 
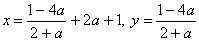
. При а=-2 уравнение не а=-2 имеет решения, если а¹-2, то 
.
Ответ: при a=-2система не имеет решения,
при а¹-2 система имеет решение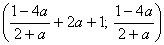 
.
Пример 6. Решить систему уравнений:
Нам дана система из трех уравнений с тремя неизвестными. Применим метод Гаусса, который состоит в том, что равносильными преобразованиями приводят данную систему к треугольной форме. Прибавим к первому уравнению второе, умноженное на –2.
Далее к третьему уравнению системы прибавим второе, умноженное на –3,
наконец прибавим к этому уравнению уравнение у-z=-1, умноженное на 2, получим — 4z=-12, z=3. Итак получаем систему уравнений:
х+у+z=6
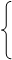
z=3, которая равносильна данной.
Система такого вида называется треугольной.
3. Решение задач с помощью уравнений и систем уравнений.
Покажем на примерах, как можно решать задачи с помощью уравнений и систем уравнений.
Пример 1. Сплав олова и меди массой 32 кг содержит 55% олова. Сколько чистого олова надо добавить в сплав, чтобы в новом сплаве щсодержалось 60% олова?
Решение. Пусть масса олова, добавленная к исходному сплаву, составляет х кг. Тогда сплав массой (32+х)кг будет содержать 60% олова и 40% меди. Исходный сплав содержал 55% олова и 45% меди, т.е. меди в нем было 32·0,45 кг. Так как масса меди в исходном и новом сплавах одна и та же, то получим уравнение 0,45·32=0,4(32+х).
Решив его, находим х=4, т.е. в сплав надо добавить 4 кг олова.
Пример 2. Задумано двузначное число, у которого цифра десятков на 2 меньше цифры единиц. Если это число разделить на сумму его цифр, то в частном получится 4 и в остатке 6. Какое число задумано?
Решение. Пусть цифра единиц есть х, тогда цифра десятков равна х-2 (х2), задуманное число имеет вид 10(х-2)+х=11х-20. Сумма цифр числа х-2+х=2х-2. Следовательно, разделив 11х-20 на 2х-2, получим в частном 4 и в остатке 6. Составляем уравнение: 11х-20=4(2х-2)+6, т.к. делимое равно делителю, умноженному на частное, плюс остаток. Решив это уравнение, получим х=6. Итак, было задумано число 46.
Пример 3. Три ящика наполнены орехами. Во втором ящике на 10% орехов больше, чем в первом, и на 30% больше, чем в третьем. Сколько орехов в каждом ящике, если в первом на 80 орехов больше, чем в третьем?
Решение. Пусть в первом ящике было х орехов, в третьем – y. Тогда во втором ящике было х+0,1х=1,1х или y+0,3y=1,3y. Учитывая, что в первом ящике было на 80 орехов больше, чем в третьем, составляем систему уравнений:
, откуда y=440, х=520, 1,1х=572.
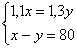
Замечание. Можно эту задачу решить, не составляя системы уравнений. Пусть в первом ящике было х орехов, тогда в третьем — х-80, во втором — 1,1х или 1,3(х-80). Имеем уравнение: 1,1х=1,3(х-80), х=520.
Ответ: в первом ящике было 520 орехов, во втором — 572, в третьем — 440.
Пример 4. Из двух городов А и В, расстояние между которыми 180 км, в 6 ч 20 мин. вышли навстречу друг другу автобус и легковой автомобиль. Их встреча произошла в 7 ч 50 мин. Если бы автобус вышел на 1 ч 15 мин. раньше, а легковой автомобиль на 15 мин. позже, то они встретились бы в 7 ч 35 мин. Какова скорость автобуса и легкового автомобиля?
Решение. Пусть скорость автобуса V1 км/ч, скорость легкового автомобиля V2 км/ч. Так как их встреча произошла через 1,5 ч, то имеем уравнение:1,5V1+1,5V2 =180. Если бы автобус вышел на 1ч 15 мин. раньше, то он был бы в пути 2 ч 30 мин. (7 ч 35 мин. – 5 ч 5 мин.= 2 ч 30 мин.). Если бы легковой автомобиль вышел на 15 мин. позже, то он был бы в пути 1 ч (7 ч 35 мин. – 6 ч 35 мин.= 1ч). Получаем уравнение: 2,5V1 +V2 =180.
Таким образом, имеем систему двух уравнений с двумя неизвестными:
, откуда V1=40 км/ч, V2=80 км/ч.
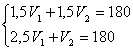
Ответ: 40 км/ч, 80 км/ч.
4. Линейные неравенства с одной переменной.
Если переменной х придать какое-либо числовое значение, то мы получим числовое неравенство, выражающее либо истинное, либо ложное высказывание. Пусть, например, дано неравенство 5х-13х+2. При х=2 получим 5·2-13·2+2 – истинное высказывание (верное числовое высказывание); при х=0 получаем 5·0-13·0+2 – ложное высказывание. Всякое значение переменной, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется решением неравенства. Решить неравенство с переменной – значит найти множество всех его решений.
Два неравенства с одной переменной х называются равносильными, если множества решений этих неравенств совпадают.
Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, более простым, но равносильным данному; полученное неравенство снова заменяем более простым равносильным ему неравенством и т.д.
Такие замены осуществляются на основе следующих утверждений.
Теорема 1. Если какой-либо член неравенства с одной переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.
Линейным называется неравенство вида ax+b0 (соответственно ax+b
Пример 1. Решить неравенство: 2(х-3)+5(1-х)³3(2х-5).
Раскрыв скобки, получим 2х-6+5-5х³6х-15,
-3х-1³6х-15, -9х³-14,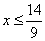 
.
Ответ: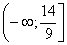 
.
Пример 2. Решить неравенство: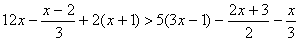 
.
Освободимся от знаменателей, для чего умножим обе части неравенства на положительное число 6, оставив без изменения знак неравенства.
, далее последовательно получаем 
; 
.
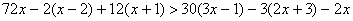
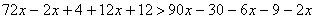
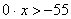
Последнее неравенство верно при любом значении х, так как при любом значении переменной х получается истинное высказывание 0-55. Поэтому множеством его решений служит вся числовая прямая.
Пример 3. Решить неравенство: ½х-1½
На основании определения модуля данное неравенство запишем в виде совокупности двух систем неравенств
(1) 
(2)
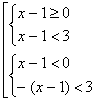
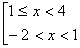
решая эту совокупность получим (2), таким образом решением этого неравенства является промежуток (-2; 4).
Пример 4. Решить неравенство:½х+1½2-х.
отсюда х0,5 из первой системы, а вторая система – не имеет решения.
5. Система и совокупности неравенств.
Говорят, что несколько неравенств с одной переменной образуют систему, если ставится задача найти множество общих решений заданных неравенств.
Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.
Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих систему. Неравенства, образующие систему, объединяются фигурной скобкой.
Например: 
Иногда используется запись в виде двойного неравенства. Например, систему неравенств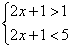 
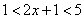
можно записать в виде двойного неравенства 
.
Говорят, что несколько неравенств с одной переменной образуют совокупность, если ставится задача найти множество таких решений, каждое из которых является решением хотя бы одного из этих неравенств.
Значение переменной, при котором хотя бы одно из неравенств, образующих совокупность, обращается в верное числовое неравенство, называется решением совокупности неравенств.
Множество решений совокупности неравенств есть объединение множеств решений неравенств, образующих совокупность. Неравенства, образующие совокупность, иногда объединяются квадратной скобкой. Так, запись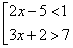 
означает, что неравенства образуют совокупность.
Пример 1. Решить систему неравенств: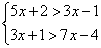 
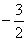
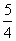
Û 
х
С помощью числовой прямой находим, что пересечением этих множеств служит интервал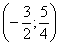 
. Это и есть множество решений данной системы.
Пример 2. Решить совокупность неравенств: 
Преобразовав каждое из неравенств, получим совокупность, равносильную данной 
х
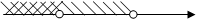
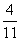
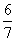
Объединением этих множеств служит промежуток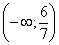 
, который и является решением совокупности неравенств.
http://infourok.ru/urok-po-teme-reshenie-linejnyh-uravnenij-i-neraventsv-5773886.html
http://kopilkaurokov.ru/matematika/uroki/linieinyie-uravnieniia-i-nieravienstva