Линейные уравнения и неравенства
Романишина Дина Соломоновна, учитель математики гимназии №2 г. Хабаровска
1. Уравнения с одной переменной.
Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.
Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.
Решить уравнение — значит найти все его корни или доказать, что корней нет.
Уравнения называются равносильными, если все корни первого уравнения являются корнями второго уравнения и наоборот, все корни второго уравнения являются корнями первого уравнения или, если оба уравнения не имеют корней. Например, уравнения х-8=2 и х+10=20 равносильны, т.к. корень первого уравнения х=10 является корнем и второго уравнения, и оба уравнения имеют по одному корню.
При решении уравнений используются следующие свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Уравнение ах=b, где х – переменная, а и b – некоторые числа, называется линейным уравнением с одной переменной.
Если а¹0, то уравнение имеет единственное решение .
Если а=0, b=0, то уравнению удовлетворяет любое значение х.
Если а=0, b¹0, то уравнение не имеет решений, т.к. 0х=b не выполняется ни при одном значении переменной.
Пример 1. Решить уравнение: -8(11-2х)+40=3(5х-4)
Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим:
Пример 2. Решить уравнения:
Эти уравнения не являются линейными, но покажем, как можно решать такие уравнения.
3х2-5х=0; х(3х-5)=0. Произведение равно нулю, если один из множителей равен нулю, получаем х1=0; х2= .
Разложить на множители левую часть уравнения:
х2(х-2)-9(х-2)=(х-2)(х2-9)=(х-2)(х-3)(х-3), т.е. (х-2)(х-3)(х+3)=0. Отсюда видно, что решениями этого уравнения являются числа х1=2, х2=3, х3=-3.
с) Представим 7х, как 3х+4х, тогда имеем: х2+3х+4х+12=0, х(х+3)+4(х+3)=0, (х+3)(х+4)=0, отсюда х1=-3, х2=- 4.
Пример 3. Решить уравнение: ½х+1ç+½х-1ç=3.
Напомним определение модуля числа:
Например: ½3½=3, ½0½=0, ½- 4½= 4.
В данном уравнении под знаком модуля стоят числа х-1 и х+1. Если х меньше, чем –1, то число х+1 отрицательное, тогда ½х+1½=-х-1. А если х>-1, то ½х+1½=х+1. При х=-1 ½х+1½=0.
а) Рассмотрим данное уравнение½х+1½+½х-1½=3 при х£-1, оно равносильно уравнению -х-1-х+1=3, -2х=3, х= , это число принадлежит множеству х£-1.
х+1+х-1=3, 2х=3, х= . Это число принадлежит множеству х>1.
Ответ: х1=-1,5; х2=1,5.
Пример 4. Решить уравнение:½х+2½+3½х½=2½х-1½.
Покажем краткую запись решения уравнения, раскрывая знак модуля «по промежуткам».
–2 1, х+2+3х=2(х-1), 2х=- 4, х=-2Ï(1; +¥)
Пример 5. Решить уравнение: (а-1)(а+1)х=(а-1)(а+2), при всех значениях параметра а.
В этом уравнении на самом деле две переменных, но считают х–неизвестным, а а–параметром. Требуется решить уравнение относительно переменной х при любом значении параметра а.
Если а=1, то уравнение имеет вид 0×х=0, этому уравнению удовлетворяет любое число.
Если а=-1, то уравнение имеет вид 0×х=-2, этому уравнению не удовлетворяет ни одно число.
Если а¹1, а¹-1, тогда уравнение имеет единственное решение .
Ответ: если а=1, то х – любое число;
если а=-1, то нет решений;
2. Системы уравнений с двумя переменными.
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему — значит найти все ее решения или доказать, что их нет. Две системы уравнений называются равносильными, если каждое решение первой системы является решением второй системы и каждое решение второй системы является решением первой системы или они обе не имеют решений.
При решении линейных систем используют метод подстановки и метод сложения.
Пример 1. Решить систему уравнений:
Для решения этой системы применим метод подстановки. Выразим из первого уравнения х и подставим это значение во второе уравнение системы, получим
Пример 2. Решить систему уравнений:
Для решения этой системы применим метод сложения уравнений. 8х=16, х=2. Подставим значение х=2 в первое уравнение, получим 10-у=9, у=1.
Пример 3. Решить систему уравнений:
Эта система равносильна одному уравнению 2х+у=5, т.к. второе уравнение получается из первого умножением на 3. Следовательно, ей удовлетворяет любая пара чисел (х; 5-2х). Система имеет бесконечное множество решений.
Ответ: (х; 5-2х), х–любое.
Пример 4. Решить систему уравнений:
Умножим первое уравнение на –2 и сложим со вторым уравнением, получим 0×х+0×у=-6. Этому уравнению не удовлетворяет ни одна пара чисел. Следовательно, эта система не имеет решений.
Ответ: система не имеет решений.
Пример 5. Решить систему:
Из второго уравнения выражаем х=у+2а+1 и подставляем это значение х в первое уравнение системы, получаем . При а=-2 уравнение не а=-2 имеет решения, если а¹-2, то .
Ответ: при a=-2система не имеет решения,
при а¹-2 система имеет решение .
Пример 6. Решить систему уравнений:
Нам дана система из трех уравнений с тремя неизвестными. Применим метод Гаусса, который состоит в том, что равносильными преобразованиями приводят данную систему к треугольной форме. Прибавим к первому уравнению второе, умноженное на –2.
Далее к третьему уравнению системы прибавим второе, умноженное на –3,
наконец прибавим к этому уравнению уравнение у-z=-1, умноженное на 2, получим — 4z=-12, z=3. Итак получаем систему уравнений:
z=3, которая равносильна данной.
Система такого вида называется треугольной.
3. Решение задач с помощью уравнений и систем уравнений.
Покажем на примерах, как можно решать задачи с помощью уравнений и систем уравнений.
Пример 1. Сплав олова и меди массой 32 кг содержит 55% олова. Сколько чистого олова надо добавить в сплав, чтобы в новом сплаве щсодержалось 60% олова?
Решение. Пусть масса олова, добавленная к исходному сплаву, составляет х кг. Тогда сплав массой (32+х)кг будет содержать 60% олова и 40% меди. Исходный сплав содержал 55% олова и 45% меди, т.е. меди в нем было 32·0,45 кг. Так как масса меди в исходном и новом сплавах одна и та же, то получим уравнение 0,45·32=0,4(32+х).
Решив его, находим х=4, т.е. в сплав надо добавить 4 кг олова.
Пример 2. Задумано двузначное число, у которого цифра десятков на 2 меньше цифры единиц. Если это число разделить на сумму его цифр, то в частном получится 4 и в остатке 6. Какое число задумано?
Решение. Пусть цифра единиц есть х, тогда цифра десятков равна х-2 (х>2), задуманное число имеет вид 10(х-2)+х=11х-20. Сумма цифр числа х-2+х=2х-2. Следовательно, разделив 11х-20 на 2х-2, получим в частном 4 и в остатке 6. Составляем уравнение: 11х-20=4(2х-2)+6, т.к. делимое равно делителю, умноженному на частное, плюс остаток. Решив это уравнение, получим х=6. Итак, было задумано число 46.
Пример 3. Три ящика наполнены орехами. Во втором ящике на 10% орехов больше, чем в первом, и на 30% больше, чем в третьем. Сколько орехов в каждом ящике, если в первом на 80 орехов больше, чем в третьем?
Решение. Пусть в первом ящике было х орехов, в третьем – y. Тогда во втором ящике было х+0,1х=1,1х или y+0,3y=1,3y. Учитывая, что в первом ящике было на 80 орехов больше, чем в третьем, составляем систему уравнений:
, откуда y=440, х=520, 1,1х=572.
Замечание. Можно эту задачу решить, не составляя системы уравнений. Пусть в первом ящике было х орехов, тогда в третьем — х-80, во втором — 1,1х или 1,3(х-80). Имеем уравнение: 1,1х=1,3(х-80), х=520.
Ответ: в первом ящике было 520 орехов, во втором — 572, в третьем — 440.
Пример 4. Из двух городов А и В, расстояние между которыми 180 км, в 6 ч 20 мин. вышли навстречу друг другу автобус и легковой автомобиль. Их встреча произошла в 7 ч 50 мин. Если бы автобус вышел на 1 ч 15 мин. раньше, а легковой автомобиль на 15 мин. позже, то они встретились бы в 7 ч 35 мин. Какова скорость автобуса и легкового автомобиля?
Решение. Пусть скорость автобуса V1 км/ч, скорость легкового автомобиля V2 км/ч. Так как их встреча произошла через 1,5 ч, то имеем уравнение:1,5V1+1,5V2 =180. Если бы автобус вышел на 1ч 15 мин. раньше, то он был бы в пути 2 ч 30 мин. (7 ч 35 мин. – 5 ч 5 мин.= 2 ч 30 мин.). Если бы легковой автомобиль вышел на 15 мин. позже, то он был бы в пути 1 ч (7 ч 35 мин. – 6 ч 35 мин.= 1ч). Получаем уравнение: 2,5V1 +V2 =180.
Таким образом, имеем систему двух уравнений с двумя неизвестными:
, откуда V1=40 км/ч, V2=80 км/ч.
Ответ: 40 км/ч, 80 км/ч.
4. Линейные неравенства с одной переменной.
Если переменной х придать какое-либо числовое значение, то мы получим числовое неравенство, выражающее либо истинное, либо ложное высказывание. Пусть, например, дано неравенство 5х-1>3х+2. При х=2 получим 5·2-1>3·2+2 – истинное высказывание (верное числовое высказывание); при х=0 получаем 5·0-1>3·0+2 – ложное высказывание. Всякое значение переменной, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется решением неравенства. Решить неравенство с переменной – значит найти множество всех его решений.
Два неравенства с одной переменной х называются равносильными, если множества решений этих неравенств совпадают.
Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, более простым, но равносильным данному; полученное неравенство снова заменяем более простым равносильным ему неравенством и т.д.
Такие замены осуществляются на основе следующих утверждений.
Теорема 1. Если какой-либо член неравенства с одной переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.
Линейным называется неравенство вида ax+b>0 (соответственно ax+b .
Пример 2. Решить неравенство: .
Освободимся от знаменателей, для чего умножим обе части неравенства на положительное число 6, оставив без изменения знак неравенства.
, далее последовательно получаем ; .
Последнее неравенство верно при любом значении х, так как при любом значении переменной х получается истинное высказывание 0>-55. Поэтому множеством его решений служит вся числовая прямая.
Пример 3. Решить неравенство: ½х-1½ (1) (2)
решая эту совокупность получим (2), таким образом решением этого неравенства является промежуток (-2; 4).
Пример 4. Решить неравенство:½х+1½>2-х.
отсюда х>0,5 из первой системы, а вторая система – не имеет решения.
5. Система и совокупности неравенств.
Говорят, что несколько неравенств с одной переменной образуют систему, если ставится задача найти множество общих решений заданных неравенств.
Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.
Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих систему. Неравенства, образующие систему, объединяются фигурной скобкой.
Иногда используется запись в виде двойного неравенства. Например, систему неравенств можно записать в виде двойного неравенства .
Говорят, что несколько неравенств с одной переменной образуют совокупность, если ставится задача найти множество таких решений, каждое из которых является решением хотя бы одного из этих неравенств.
Значение переменной, при котором хотя бы одно из неравенств, образующих совокупность, обращается в верное числовое неравенство, называется решением совокупности неравенств.
Множество решений совокупности неравенств есть объединение множеств решений неравенств, образующих совокупность. Неравенства, образующие совокупность, иногда объединяются квадратной скобкой. Так, запись означает, что неравенства образуют совокупность.
Пример 1. Решить систему неравенств: Û
С помощью числовой прямой находим, что пересечением этих множеств служит интервал . Это и есть множество решений данной системы.
Пример 2. Решить совокупность неравенств:
Преобразовав каждое из неравенств, получим совокупность, равносильную данной
Объединением этих множеств служит промежуток , который и является решением совокупности неравенств.
6. Неравенства и системы неравенств с двумя переменными.
Известно, что пара действительных чисел (х0; у0) однозначно определяет точку координатной плоскости. Это дает возможность изображать множество решений неравенства или системы неравенств с двумя переменными геометрически, в виде некоторого множества точек координатной плоскости.
Пример 1. Дать геометрическую интерпретацию решения неравенства .
Преобразуем данное неравенство к виду .
Построим в прямоугольной системе координат прямую .
Так как ордината любой точки, лежащей выше прямой , больше, чем ордината точки, лежащей на прямой и имеющей такую же абсциссу, то множество точек плоскости, расположенных выше этой прямой и служит геометрической интерпретацией решения заданного неравенства.
Геометрическая интерпретация позволяет записать решение в виде
(для составления второй записи нужно преобразовать уравнение к виду, разрешенному относительно х).
Пример 2. Решить систему неравенств:
Найдем на координатной плоскости пересечение областей , получим геометрическое решение заданной системы неравенств.
Для того, чтобы записать решения, найдем координаты точек пересечения линий , .
Решив систему уравнений найдем координаты искомых точек: (1; 4) и (4; 1), таким образом приходим к системе
Задания для самостоятельного решения
Приведенные ниже задачи, являются контрольным заданием. Необходимо решить все задачи, однако, если это не удалось, присылайте те, которые решены. Правила оформления работ смотрите во вступительной статье.
М9.1.1 Решить уравнения:
М9.1.2 Указать, при каких значениях параметра а уравнение имеет бесконечно много решений:
М9.1.3 Указать, при каких значениях параметра а уравнение не имеет решений:
М9.1.4 Решить систему уравнений:
М9.1.5 При каких значениях параметра а система имеет бесконечно много решений?
М9.1.6 Решить задачи:
а) сплав состоит из цинка и меди, входящих в него в отношении 1:2, а другой сплав содержит те же металлы в отношении 2:3. Из скольких частей обоих сплавов можно получить третий сплав, содержащий те же металлы в отношении 17:27?
б) расстояние между пристанями А и В теплоход проходит по течению за 5 ч, а против течения за 6 ч. За сколько часов проплывет по течению это расстояние плот?
М9.1.7 Решить неравенство:
М9.1.8 Решить совокупность неравенств:
М9.1.9 Найти геометрические решения систем неравенств и, по крайней мере, один из видов записи решений:
Реферат » Решение уравнений и неравенств графическим способом» ( 9 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
МБОУ Алтайская СОШ №1
Тема : « Графическое решение уравнений и неравенств»
Учащаяся 9 а класса
МБОУ Алтайская СОШ №1
Бабаева Галина Яковлевна,
МБОУ Алтайской СОШ №1
С. Алтайское , Алтайский район, 2019 год.
II . Основная часть
2. Как графически решить уравнение________________________стр.4
3. Какие бывают функции ?________________________________стр.4
4. Графическое решение линейного уравнения с одной переменной.стр.5
5. Решение квадратного уравнения графическим способом._____ стр6-8
6. Графическое решение смешанных уравнений._______________стр.8-12. 7. Решение квадратных неравенств графическим способом_______стр.13
8. Решение линейных неравенств графическим способом стр 14
IV . Список литературы______________________________________стр.16
Цель моей работы – изложить графический метод решения уравнений и неравенств, который дает возможность определить корни или доказать ,что уравнение корней не имеет ( или решением неравенства является пустое множество).
Актуальность темы : графический метод, опирающийся на знания элементарных функций, удобно применять при решении задач на нахождение числа корней и на нахождение корней уравнений.
Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес. В данной исследовательской работе я показала как наиболее удобным способом преобразовывать уравнения . чтобы сводить к построению элементарных функций.
Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков не ограничивается только этим. В ряде случаев графики облегчают нахождение решений уравнений и неравенств, сокращая и упрощая аналитические выкладки, и часто при этом являются единственным методом решения таких задач. Данный метод может использоваться не только для одиночных уравнений, но и для их систем, а также неравенств
Уравнение – выражение, содержащее переменную.
Решить уравнение – это значит найти все его корни, или доказать, что их нет.
Корень уравнения – это число, при подстановке которого в уравнение получается верное числовое равенство.
График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргументов, а ординаты – соответствующим значениям функции.
Решение уравнений графическим способом позволяет найти точное или приближенное значение корней, позволяет найти количество корней уравнения.
При построении графиков и решении уравнений используются свойства функции, поэтому метод чаще называют функционально-графическим. Графиком функции y = f(x) называется множество всех точек
Заметим , что так как функция f сопоставляет каждому x D(f) одно число f(x) , то график функции f пересекается любой прямой, параллельной оси ординат, не более, чем в одной точке. И наоборот: всякое непустое множество точек плоскости, имеющее со всякой прямой, параллельной оси ординат, не более одной общей точки, является графиком некоторой функции.
Не всякое множество точек координатной плоскости является графиком какой-либо функции. Например, множество точек окружности не может быть графиком функции, поскольку значению абсциссы внутри окружности, соответствует два значения ординаты.
В общем случае уравнение с одной переменой х можно записать в виде f(x)=g(x),где f(x) и g(x) — некоторые функции. Функция f(x) является левой частью , а g(x) — правой частью уравнения.
Тогда для решения уравнения необходимо построить в одной системе координат графики функций f(x) и g(x). Абсциссы точек пересечения будут являться решениями данного уравнения.
Использование монотонности функций при решении уравнений: если функция 


2. Как графически решить уравнение.
Иногда уравнения решают графическим способом. Для этого надо преобразовать уравнение так (если оно уже не представлено в преобразованном виде), чтобы слева и справа от знака равенства стояли выражения, для которых легко можно нарисовать графики функций. Графическим решением уравнения являются абсциссы точек пересечения графиков построенных функций. Графики могут пересекаться в нескольких точках, в одной точке, вообще не пересекаться. Отсюда следует, что уравнение может иметь несколько корней, или один корень, или вообще их не иметь.
3. Какие бывают функции .
Линейная функция задаётся уравнением у = k*x+ b , где k и b – некоторые числа. Графиком этой функции является прямая. Для построения прямой достаточно в таблице значений взять только две точки. Это вытекает из аксиомы планиметрии
Функция обратной пропорциональности у =k/x , где. График этой функции называется гиперболой.
Функция (х– a)^2+ (у – b)^2 = r^2 , где а , b и r – некоторые числа. Это окружность радиуса r с центром в т. А ( а , b ).
Квадратичная функция y = a *х 2 + b*x+ c , где а, b, с – некоторые числа и
а не равно 0. Графиком этой функции является парабола.
Графики линейных функций, содержащих выражение под знаком модуля.
Для построения графиков функций, содержащих выражение под знаком модуля, сначала находят корни выражений, стоящих под знаком модуля. Эти корни разбивают числовую прямую на промежутки. График строят в каждом промежутке отдельно.
В простейшем случает, когда только одно выражение стоит под знаком модуля и нет слагаемых без знака модуля, можно построить график функций,
опустив знак модуля, а затем часть графика, расположенного в области отрицательных значений y , отобразить симметрично оси ОХ.
Элементарная функций, содержащая модуль :
4. Графическое решение линейного уравнения с одной переменной.
Как мы уже знаем, графиком линейного уравнения является прямая линия, отсюда и название данного вида. Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и уравнение решено. Мы нашли корень .А я покажу , как это сделать графическим способом.
Задание . Решить графическим способом уравнение : 2 x − 10 = 2
1)Перенесем слагаемые следующим образом: 2 x = 12.
2) Построим графики функций: y=2x и y=12.
Но можно решать и по-другому.
Для рассмотрения альтернативного решения вернемся к нашему уравнению:
Построим графики функций: y=2 x − 10 y =2
5. Решение квадратного уравнения графическим способом.
Для этого преобразуем уравнение к виду: х 2 =-2x+8 . Построим графики функций: у = -2x+8 и у = х 2
Получим точки пересечения графиков данных функций.
В ответ запишем абсциссы этих точек : x = -4 и x =2.
Данное уравнение можно решить , переписав уравнение следующим образом: x^2 – 8 = -2x
Тогда будем строить графики функций: y = x^2 – 8 и y = -2x.
А также уравнение можно решить , переписав следующим образом:
Тогда будем строить графики следующих функций : y = x^2 + 2x и y = 8 .
При этом абсциссы точек пересечения графиков будут одинаковые :
Задание. Решить уравнение: x² – 2x = 0
Перепишем уравнение в виде : x² = 2x
Построим графики функций y = x² и y = 2 и найдем точки их пересечения :
Задание. Решить уравнение: х 2 +2=0
Преобразуем так: х 2 = -2
Построим графики функций: у=-2 и у= х 2
Графики функций не пересекаются ,поэтому уравнение решений не имеет.
Ответ : решений нет.
6. Графическое решение смешанных уравнений.
Задание. Решить уравнение: 3/х +2 =х
1)Перенесем слагаемые таким образом: 3/ х = х-2
2) Построим графики функций от каждой части уравнения.
Найдем координаты точек пересечения графиков данных функций.
Из построения видно, что графики функций пересекаются в точках с координатами : (3;1) и(-1;-3).
Задание. Решить уравнение: 2 х^3 – x — 1=0
Перепишем его так : 2 х 3 = x + 1
Построим графики функций от левой и правой части уравнения:
у= 2 х 3 (графиком этой функции является кубическая парабола) и график от правой части уравнения :у=х+1
Из построения видно, что абсцисса точки пересечения является х=1. значит, в ответ нужно записать: х=1
Решим графическим способом такое уравнение : х 3 =8.
Строим графики функций: у = х 3 и у=8., затем найдем абсциссу точки пересечения графиков этих функций.
Задание. Решить уравнение: √x – 0.5x = 0
Перепишем так: √x = 0.5x
Построим графики функций: у= 0.5x и у = √x
Как видно из построения, графики функций пересекаются в двух точках:
Нас интересует только координата x.
Значит уравнение √x – 0.5x = 0 имеет два корня: x 1 = 0 и x 2 = 4.
7. Решение квадратных неравенств графическим способом.
Способ , который нам хорошо известен при изучении данной темы по учебнику.
Я же предлагаю переписать неравенство следующим образом : х^2-4>3х.
Построим графики функций от левой и правой частей неравенства.
Выделим ту часть, где график от левой части выше графика от правой части.
На мой взгляд такое решение более красивое , интересное и более понятное.
8. Решение линейных неравенств и систем неравенств графическим способом.

Называют ся линейными неравенствами .
График линейного или квадратного неравенства строится так же, как строится график любой функции (уравнения).
Разница заключается в том, что неравенство подразумевает наличие множества решений, поэтому график неравенства представляет собой не просто точку на числовой прямой или линию на координатной плоскости.
С помощью математических операций и знака неравенства можно определить множество решений неравенства
Вообще графический способ решения неравенств с одной переменной применяется не только для решения квадратных неравенств, но и неравенств других видов.
Суть графического способа решения неравенств следующая:
рассматривают функции y = f(x) и y = g(x) , которые соответствуют левой и правой частям неравенства, строят их графики в одной прямоугольной системе координат и выясняют, на каких промежутках график одной из них располагается ниже или выше другого.
Те промежутки, на которых график функции у = f (х) выше графика функции y = g(х) являются решениями неравенства f(x)>g(x) ;
график функции y = f(х) не ниже графика функции y = g(x) являются решениями неравенства f(x) ≥ g(x) ;
график функции у = f (х) ниже графика функции y = g(х) являются решениями неравенства f(x) ;
график функции y = f(х) не выше графика функции y = g(х) являются решениями неравенства f(x) ≤ g(x) .
Также скажем, что абсциссы точек пересечения графиков функций y = f(x) и y = g(x) , являются решениями уравнения f(x) = g(x) .
Мы рассмотрели графический метод решения уравнений и квадратных неравенств; рассмотрели конкретные примеры, при решении которых использовали некоторые свойства функций.
Иногда при графическом решении некоторых уравнений и неравенств корни определяются только приближённо в силу того, что невозможно с высокой точностью построить график функции, измерить абсциссы или ординаты точек пересечения графика с осями координат или с другими графиками. Тем не менее, той точности, которую обеспечивает графический метод, бывает вполне достаточно для практических нужд.
Построение графиков основывается на знании основных элементарных функций, и на основные методы построения графиков функций. В работе представлено достаточное количество примеров, раскрывающих графический метод решения линейных и квадратных уравнений и неравенств, который доступен для понимания .
Работа может быть использована для углубления и расширения знаний в области построения графиков функций и использовании графического метода при решении некоторых видов уравнений и неравенств. Теорию можно использовать так же при подготовки к экзаменам , к олимпиадам.
Я свою работу представляла учащимся 8-х и 9-х классов нашей школы. И продолжаю дополнять свои исследования , а именно находить красивые решения линейных неравенств и систем неравенств.
Это и закрепление изученных свойств функций, и прекрасная демонстрация их применения на практике.
В старших классах я буду ещё знакомиться с другими функциями , с другими уравнениями и неравенствами и м не интересно будет продолжить свой проект.
Claw.ru | Рефераты по математике | Линейные уравнения и неравенства
Линейные уравнения и неравенства
| Категория реферата: Рефераты по математике
| Теги реферата: инновационная деятельность, реферат анализ
| Добавил(а) на сайт: Альвина.
Линейные уравнения и неравенства
Романишина Дина Соломоновна, учитель математики гимназии №2 г. Хабаровска
1. Уравнения с одной переменной.
Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.
Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.
Решить уравнение — значит найти все его корни или доказать, что корней нет.
Уравнения называются равносильными, если все корни первого уравнения являются корнями второго уравнения и наоборот, все корни второго уравнения являются корнями первого уравнения или, если оба уравнения не имеют корней. Например, уравнения х-8=2 и х+10=20 равносильны, т.к. корень первого уравнения х=10 является корнем и второго уравнения, и оба уравнения имеют по одному корню.
При решении уравнений используются следующие свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Уравнение ах=b, где х – переменная, а и b – некоторые числа, называется линейным уравнением с одной переменной.
Если а¹0, то уравнение имеет единственное решение 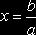
Если а=0, b=0, то уравнению удовлетворяет любое значение х.
Если а=0, b¹0, то уравнение не имеет решений, т.к. 0х=b не выполняется ни при одном значении переменной.
Пример 1. Решить уравнение: -8(11-2х)+40=3(5х-4)
Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим:
Пример 2. Решить уравнения:
Эти уравнения не являются линейными, но покажем, как можно решать такие уравнения.
3х2-5х=0; х(3х-5)=0. Произведение равно нулю, если один из множителей равен нулю, получаем х1=0; х2=
Ответ: 0; 
Разложить на множители левую часть уравнения:
Рекомендуем скачать другие рефераты по теме: скачать дипломную работу на тему, матершинные частушки.
http://infourok.ru/referat-reshenie-uravneniy-i-neravenstv-graficheskim-sposobom-klass-3684418.html
http://claw.ru/referatti/enciklopediya-referatov/matematika/referaty-referaty-po-matematike-lineynye-uravneniya-i-neravenstva.html












