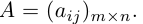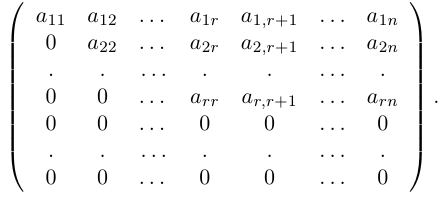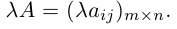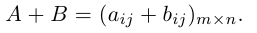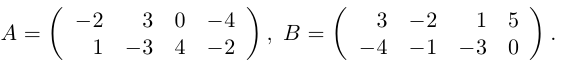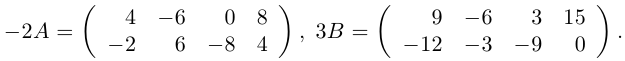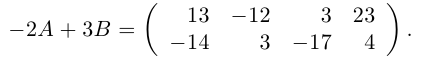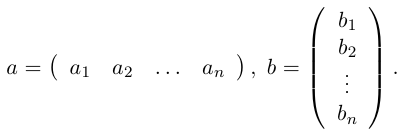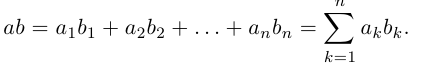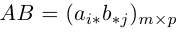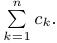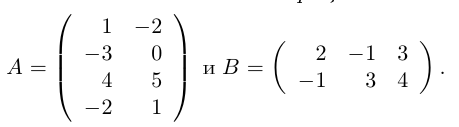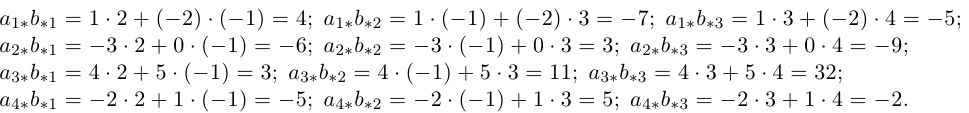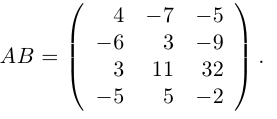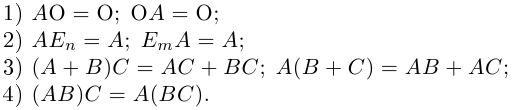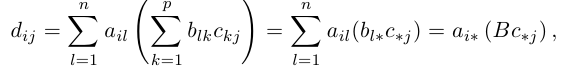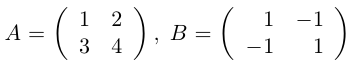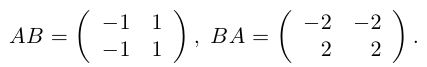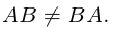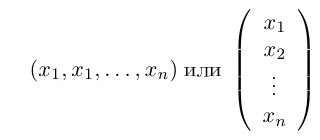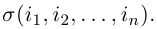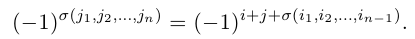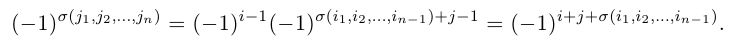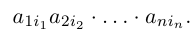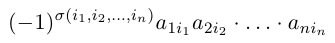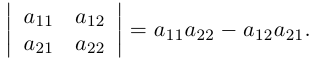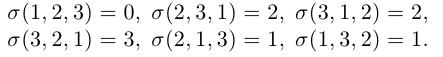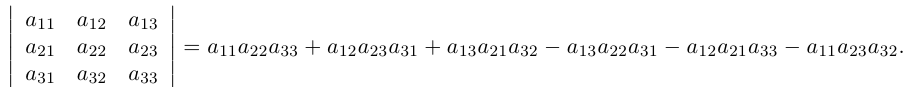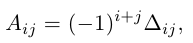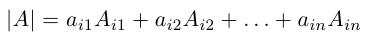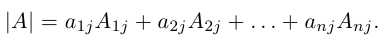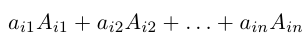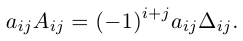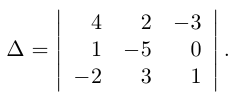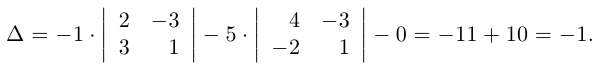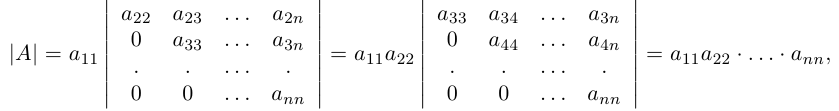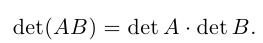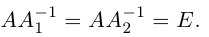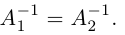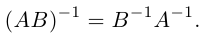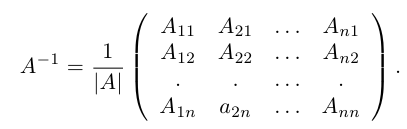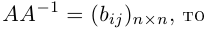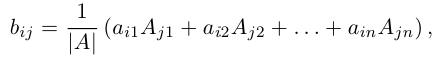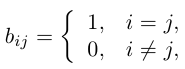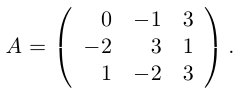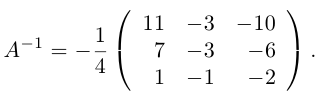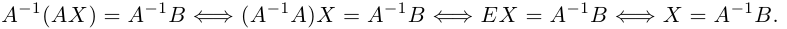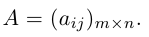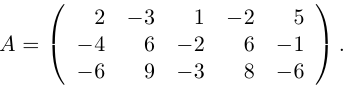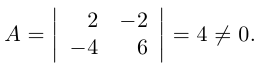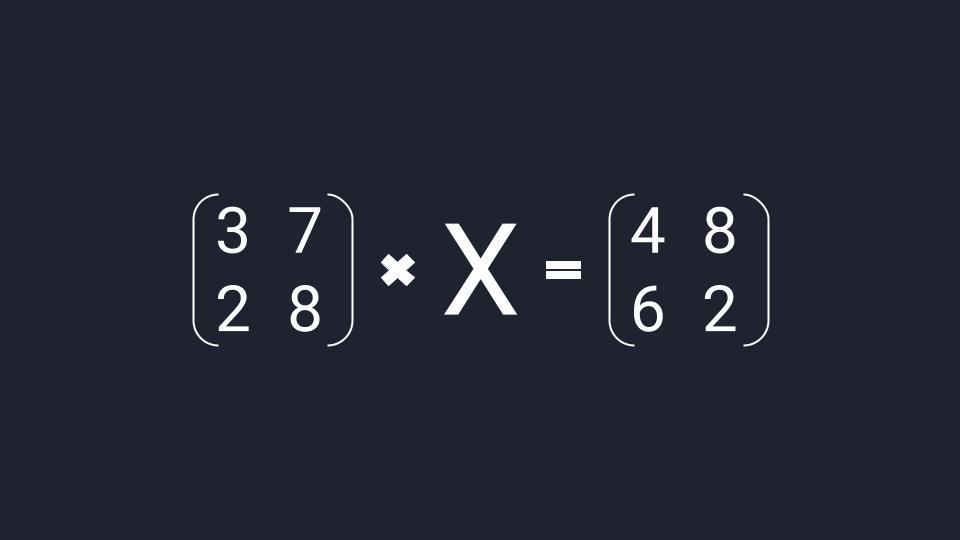Линейные уравнения линейная алгебра матрица

Линейная алгебра — примеры с решением заданий и выполнением задач

Содержание:

Линейная алгебра

Линейная алгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения, системы линейных уравнений, среди основных инструментов, используемых в линейной алгебре — определители, матрицы, сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры.

Матрицы и операции над ними

В математике и ее приложениях наряду с числами часто бывает удобным использовать чис­ловые таблицы, которые называются матрицами. Аппарат теории матриц эффективно приме­няется, например, при решении систем линейных уравнений, как мы скоро в этом убедимся. Перейдем к точным определениям.

Определение: Матрицей размерности m х n называется прямоугольная таблица дейст­вительных чисел, состоящая из m строк и n столбцов.

Числа, составляющие матрицу, называются ее элементами. Для доступа к элементам мат­рицы используются два индекса: первый указывает на номер строки, второй — на номер столб­ца, на пересечении которых расположен данный элемент.

Обозначаются матрицы, как правило, прописными латинскими буквами A, B, C,иногда указывается размерность, например, Amxn. В развернутой форме матрица записывается как таблица:

Более компактно с указанием элементов матрица записывается в виде:

Матрицы А и В одинаковой размерности считаются равными, если все элементы одной матрицы равны соответвующим элементам другой матрицы.

Рассмотрим некоторые специальные виды матриц.

Матрица, у которой все элементы равны нулю, называется нуль-матрицей и обозначается через O.

Матрица, у которой число строк равно числу столбцов, называется квадратной. Размерность квадратной матрицы часто называют ее порядком.

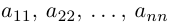
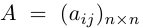
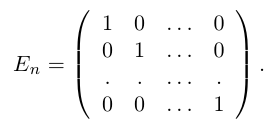
Числа в квадратной матрице называются диагональными элементами. Совокупность диагональных элементов составляет главную диагональ квадрат­ной матрицы.

Квадратная матрица, диагональные элементы которой равны единице, а все остальные — нулю, называется единичной матрицей и обозначается через 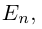где n — порядок матрицы.

Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (выше) главной диагонали, равны нулю. Например, треугольной является матрица

Матрица называется трапециевидной, если она представляет собой следующую таблицу:

Операции над матрицами

Введем сначала линейные операции над матрицами.

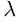
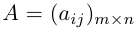
Произведением действительного числа на матрицу называется матрица

Суммой двух матриц 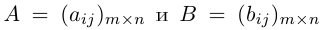одинаковой размерности называется матрица

Таким образом, элементы суммы матриц равны суммам соответствующих элементов данных матриц.

Разность матриц А и B можно определить как А — В = А + (-1)В.

Свойства линейных операций над матрицами аналогичны соответствующим свойствам действительных чисел.

Пример №1

Найти матрицу -2А +3В.

Определим теперь операцию умножения матриц. Рассмотрим сначала матрицу-строку и матрицу-столбец с одинаковым числом элементов, т.е.

Произведением этих строки и столбца называется число1

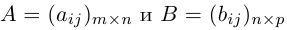
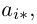
Рассмотрим так называемые согласованные матрицы , у первой из которых число столбцов равно числу строк второй матрицы. Обозначим строку с номером i матрицы А через а столбец с номером j матрицы B через

Произведением данных согласованных матриц А и B называется матрица

Часто для суммы n чисел 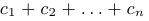мы будем использовать короткое обо значение

размерности m х p, элементы которой равны произведениям строк матрицы A на столбцы B.

Пример №2

Найти произведение согласованных матриц

Решение. Найдем произведение строк матрицы А на столбцы матрицы В.

Осталось записать искомое произведение матриц:

Отметим некоторые свойства произведения матриц1.

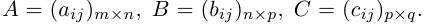
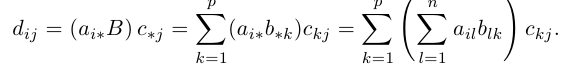
Первые три сразу следуют из определения произведения матриц. Докажем последнее свой­ство. Пусть заданы три матрицы Элемент dij произ­ведения (AB)C равен произведению строки с номером i матрицы AB на столбец с номером j матрицы C : Поменяв порядок суммирования в последней двойной сумме, получим:

что представляет собой произведение Тем строки с номером i матрицы A на столбец с номером j матрицы ВС. Тем самым свойство 4 доказано.

Заметим, что в отличие от чисел матрицы, вообще говоря, не коммутируют (не переста­новочны). Приведем соответствующий

Контрпример. Доказать, что матрицы

Таким образом, для этих матриц

Замечание. Пользуясь случаем, введем здесь определение n-мерного векторного пространства Rn, как множество упорядоченных совокупностей n действительных чисел. Каждую такую совокупность мы будем обозначать через и называть n-мерным вектором.

Мы предполагаем, что все матрицы в свойствах согласованы.

Очевидно, каждый вектор мы можем отождествить с соответствующей матрицей-строкой или матрицей-столбцом, поэтому на векторы автоматически переносятся линейные операции, которые мы определили выше для матриц.

Определитель матрицы и его свойства

Познакомимся теперь с такой важнейшей характеристикой матрицы, как определитель. Вве­дем предварительно понятие перестановки и изучим некоторые ее свойства.

Перестановки

Перестановкой n натуральных чисел 1, 2, . n называется строка

(1)

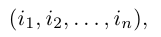
содержащая все эти числа.

Первым элементом перестановки может быть любое из чисел 1, 2, . n, вторым — любое из оставшихся n — 1 чисел и так далее, следовательно, число различных перестановок данных чисел равно (читается n-факториал).

Два числа в перестановке находятся в инверсии, если большее из них имеет меньший номер. Число всех инверсий в перестановке (1) мы обозначим через

В связи с этим перестановка (1) называется четной, если в ней число 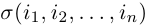четно и нечетной — в противном случае.

Отметим два свойства перестановок, которые мы будем использовать ниже.

Лемма 1. Характер четности перестановки изменится на противоположный, если в ней поменять местами какие-нибудь два элемента.

Доказательство. Предположим сначала, что меняются местами рядом стоящие элементы к и l перестановки. В этом случае число инверсий в новой перестановке изменится на единицу, а именно, увеличится на единицу, если к и l не находились в инверсии, или на­столько же уменьшится, если они находились в инверсии. Таким образом, характер четности перестановки изменится на противоположный. Рассмотрим теперь случай, когда числа к и l разделяют s других элементов перестановки. Тогда поменять местами данные элементы мы можем последовательно переставляя число к с s промежуточными элементами, а затем пере­ставляя число l в обратном порядке с элементом к и всеми s промежуточными. В результате мы выполним 2s + 1 обменов рядом стоящих элементов и, таким образом, характер четно­сти исходной перестановки изменится нечетное число раз и, следовательно, он изменится на противоположный. Лемма доказана.

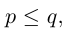
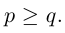
Из этой леммы сразу же следует, что количество четных перестановок равно количеству нечетных. В самом деле, поменяв местами любые два элемента в каждой из p четных переста­новок, мы получим p нечетных и, следовательно, где q — количество нечетных перестано­вок. Аналогично мы можем убедиться в справедливости неравенства Из этих неравенств и следует, что p = q.

Лемма 2. Пусть

(2)

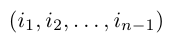
— перестановка чисел 1, 2, . n — 1. Зафиксируем число j из множества <1, 2, . , n>и оставим его перестановку (2) на место с номером i, сдвинув вправо на одну позицию все ее элементы с номерами i, i + 1, . , n — 1 и увеличив на единицу все не меньшие, чем j элемен­ты этой перестановки. В результате получим перестановку

(3)

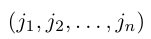
чисел 1, 2, . , n. Четности перестановок (2) и (3) связаны равенством

Действительно, предположим сначало, что элемент j в перестановке (3) стоит на первом месте. Тогда, очевидно, количество инверсий в этой перестановке равно 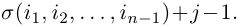Перегоним теперь число j на место с номером i, последовательно обменивая его со следующими i — 1 элементами. По лемме 1 характер четности перестановки изменится i — 1 ра и, значит,

Определитель и его вычисление для матриц второго и третьего порядков

Рассмотрим квадратную матрицу порядка n :

Составим произведение элементов данной матрицы, взятых по одному из каждой строки и каждого столбца. Упорядочив элементы этого произведения по возрастанию номеров строк, мы можем записать его в виде:

Номера столбцов в записанном произведении образуют перестановку чисел 1, 2, . , n.

Определение: Число, равное сумме всех n! произведений

называется определителем данной квадратной матрицы А (определителем n-го порядка) и обозначается через |А| или det А. В развернутой форме определитель записывается как

Найдем пользуясь этим определением выражение для определителей второго и третьего порядков.

Так как 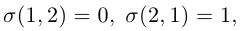то

Аналогично, для вычисления определителя третьего порядка найдем число инверсий в каждой из перестановок чисел 1, 2, 3 :

Тогда

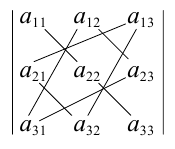
Для упрощения вычисления определителя третьего порядка можно использовать правило треугольников, согласно которому со знаком » + » следует брать произведения по схеме

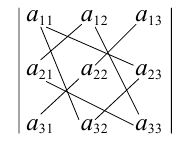
а со знаком » — » — по схеме

Пример №3

Решение. Воспользуемся правилом треугольников: = —2 + 6 — 6 — 9 — 8 — 1 = -20.

Свойства определителя

1) Если какая-либо строка (столбец) определителя состоит из нулей, то и определитель равен нулю.

2) Общий множитель элементов какой-либо строки (столбца) можно выносить за знак определителя.

3) Если все элементы какой-нибудь строки (столбца) определителя равны суммам двух слагаемых, то данный определитель равен сумме двух определителей, в которых в указан­ной строке (столбце) стоят, соответственно, первые и вторые слагаемые, а остальные элементы обоих определителей такие же, как и в исходном определителе.

Эти свойства напрямую следуют из определения определителя.

4) Если переставить две какие-нибудь строки (столбца) определителя, то он поменяет знак на противоположный.

Действительно, переставим, например, две строки определителя. В результате получим определитель, каждое слагаемое которого отличается знаком от соответствующего слагаемого исходного определителя, так как по доказанной в пункте 1 лемме 1 четность соответствующей перестановки вторых индексов изменится па противоположную.

5) Если в определителе совпадают (пропорциональны) две какие-нибудь строки (столбцы), то этот определитель равен нулю.

В самом деле, если в определителе совпадают две каие-нибудь строки (столбцы), то, с одной стороны, определитель при этом не изменится, а, с другой стороны, по предыдущему свойству его знак поменяется на противоположный. Таким образом |A| = — |A| и, стало быть, |A| = 0. Если же в определителе имеются две пропорциональные строки (столбца), то после вынесе­ния за его знак по свойству 2) общего множителя элементов строки (столбца), мы получим определитель с двумя одинаковыми строками (столбцами), который равен нулю.

6) Определитель не изменится, если к элементам какой-нибудь строки (столбца) доба­вить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.

Это следует из свойств 3) и 5), так как в этом случае полученный определитель можно представить в виде суммы двух определителей, один из которых равен исходному, а в другом имеются пропорциональные строки (столбцы), и поэтому он равен пулю.

Прежде чем сформулировать очередное свойство, введем понятие алгебраического дополне­ния к элементу матрицы.

Алгеброическим дополнением элемента aij квадратной матрицы A = (aij)nxn мы будем называть число

где 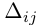— определитель порядка n — 1, полученный из определителя этой матрицы вычеркиванием i-ой строки и j-го столбца.

7) Разложение определителя по элементам строки (столбца).

Определитель матрицы равен сумме произведений элементов какой-нибудь строки (столб­ца) на соответствующие алгебраические дополнения. Таким образом,

Докажем, например, первую из этих формул. Убедимся в том, что правая часть данной формулы содержит все слагаемые определителя матрицы А. Выражение

содержит n(n — 1)! = n! различных произведений элементов определи теля матрицы A, взятых по одному из каждой строки и каждого столбца. Осталось проверить соответствие знаков.

Рассмотрим произвольное произведение

Каждое слагаемое определителя 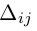представляет собой произведение элементов данной мат­рицы, взятых по одному из каждой строки и каждого столбца, исключая строку с номером i и столбец с номером j. Знак этого произведения определяется четностью перестановки

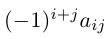
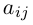
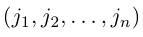
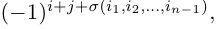
чисел 1, 2, . , n — 1. Умножив данное произведение на число и поставив множитель на место с номером i, мы получим соответствующее произведение определителя матрицы А с перестановкой вторых индексов и знаком который по лемме 2 пункта 1 соответствует четности перестановки

Таким образом, вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка.

Пример №4

Решение. Разложим этот определитель по элементам второй строки:

Пример №5

Вычислить определитель треугольной матрицы

Разлагая этот и следующие определители по первому столбцу, получим:

таким образом, определитель треугольной матрицы равен произведению диагональных эле­ментов.

8) Сумма произведений n действительных чисел на алгебраические дополнения к элементам какой-нибудь строки (столбца) равна определителю, в котором в указанной строке (столбце) расположены данные числа, а все остальные элементы совпадают с соответствующими элементами исходного определителя.

Это свойство является прямым следствием предыдущего.

9) Сумма произведений элементов какой-нибудь строки (столбца) на алгебраические до­полнения к элементам какой-нибудь другой строки (столбца) определителя равна нулю.

Действительно, по предыдущему свойству эта сумма произведений равна определителю с двумя совпадающими строками (столбцами), а такой определитель по свойству 5) равен нулю.

10) Определитель произведения матриц равен произведению определителей этих матриц, т. е.

Достаточно громоздкое доказательство этого свойства мы приводить не будем.

Обратная матрица

Определение: Обратной к квадратной матрице 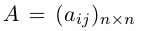называется обозначаемая через А-1 матрицы, для которой АА-1 = А-1А = Е, где Е — единичная матрица.

Из этого определения следует, что матрица А-1 также является квадратной той же размер­ности, что и матрица А.

Отметим некоторые свойства обратной матрицы, следующие из ее определения.

а) У матрицы не может существовать больше одной обратной.

Действительно, пусть для матрицы А имеются две обратные 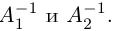Тогда

Умножив обе части первого равенства слева на матрицу 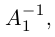получим

c) Если для квадратных матриц А и В одного порядка существуют обратные, то и у матрицы АВ также существует обратная , причем

Выясним условия, при которых обратная матрица существует.

Теорема (критерий существования обратной матрицы). Для того, чтобы существовала матрица, обратная данной, необходимо и достаточно, чтобы данная матрица была невырожденной, то есть чтобы ее определитель был не равен нулю.

Доказательство. Докажем сначала необходимость условия теоремы. Пусть для матрицы А существует обратная матрица. Тогда из равенства АА-1 = E, воспользовавшись свойством 10) определителя произведения матриц, получаем: det(AA-1) = det А det А-1 = det E = 1. Следователь но, det А 0.

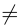
Убедимся теперь в том, что условие теоремы является и достаточным. Предположим, что матрица А является невырожденной. Проверим, что обратной к данной является матрица со следующей структурой 1:

Действительно, если

откуда, воспользовавшись свойствами 7) и 9) определителя (§2, пункт 3), заключаем:

т. е. АА-1 = Е. Аналогично убеждаем, что А-1А = Е. Теорема доказана.

В строках указанной ниже матрицы записаны алгебраические дополнения к элементам соответствующих столбцов.

Пример №6

Найти обратную к матрице

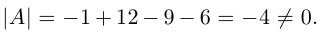
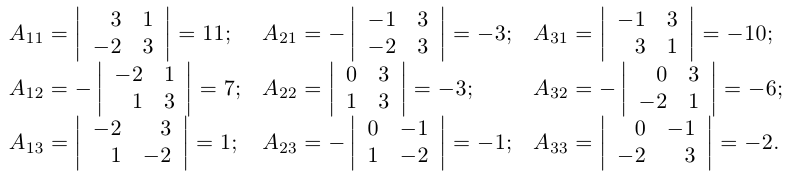
Решение. Найдем сначала определитель матрицы: Обратная матрица существует. Находим алгебраические дополнения к элементам данной матрицы:

Следовательно,

Обратную матрицу можно использовать при решении линейных матричных уравнений. Пусть, например, требуется решить матричное уравнение

с известными матрицами А и B, причем матрица A является невырожденной. Умножая обе части данного матричного уравнения слева на обратную матрицу A-1, получим:

Аналогично, решением матричного уравнения XA = B является матрица X = BA-1, а ре­шением матричного уравнения AXB = С с невырожденными матрицами A и B является матрица X = A-1CB-1.

Ранг матрицы и его вычисление

Рассмотрим произвольную матрицу

Минором порядка k матрицы A называется определитель, стоящий на пересечении выбран­ных k строк и k столбцов данной матрицы.

Определение: Рангом матрицы А называется максимальный из порядков ненулевых миноров этой матрицы. Обозначается ранг через rang A.

Естественно считать, что rang O = 0. Очевидно также, что

Пример №7

Найти ранг матрицы

Решение. Вычислим минор, находящийся на пересечении первых двух строк и первого и четвертого столбцов:

Все же миноры третьего порядка этой матрицы равны нулю, так как третья строка равна разности второй и первой строк. Следовательно, rang A = 2.

Как видно из определения, вычисление ранга матрицы через миноры является весьма тру­доемкой задачей, особенно для матриц большой размерности. Значительно сократить объем вычислений позволяет другой метод, основанный на элементарных преобразованиях матрицы.

Элементарными преобразованиями матрицы называются следующие операции над ее стро­ками или столбцами:

1. перестановка двух строк (столбцов) матрицы;
2. умножение строки (столбца) на ненулевое действительное число;
3. добавление к строке (столбцу) другой строки (столбца), умноженной на действительное число.

Тот факт, что матрица В получена из матрицы А с помощью одного или нескольких последовательно выполненных элементарных преобразований, мы будем обе тачать как

Теорема. Ранг матрицы не меняется при ее элементарных преобразованиях.

Доказательство этого утверждения для первого и второго элементарных преобразований следует из того, что по свойствам 2) и 4) определителя (§2, пункт 3) миноры исходной матрицы могут отличаться от миноров преобразованной разве лишь знаком или ненулевым множителем, что. естественно, не отражается на ранге матрицы. 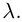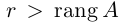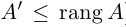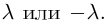Пусть теперь матрица А’ получена из матрицы А с помощью третьего элементарного преобразования, для определенности будем считать, что к строке с номером i добавлена строка с номером j, умноженная на действительное число Возьмем в матрице А’ минор М порядка (если такого минора нет, то rang ). Этот минор либо совпадает с минором матрицы A, либо по свойствам 3). 2). 4) определителя он равен сумме двух миноров матрицы А с действительными коэффициентами, один из которых равен 1. а второй В обоих случаях по определению ранга матрицы минор М равен 0. Следовательно, rang А’ n.

Следствие: Для того чтобы однородная система n уравнений с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы ее основной определитель был равен нулю.

Доказательство:

Достаточность: 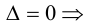система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Линейные уравнения. Решение систем линейных уравнений матричным методом.

Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.

Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.

Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем:

Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем):

Значит, её легко перевести в матричную форму:

AX=B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B.

Т.к. A −1 A=E, значит, X=A −1 B. Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A. Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A:

Для однородной системы линейных уравнений, т.е. если вектор B=0, выполняется обратное правило: у системы AX=0 есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0. Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.

Т.о., решение СЛАУ матричным методом производится по формуле . Либо, решение СЛАУ находят при помощи обратной матрицы A −1 .

Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.

Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.

Пример решения неоднородной СЛАУ.

Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.

Далее вычисляем алгебраические дополнения для элементов матрицы, которая состоит из коэффициентов при неизвестных. Эти коэффициенты нужны будут для вычисления обратной матрицы.

Теперь находим союзную матрицу, транспонируем её и подставляем в формулу для определения обратной матрицы.

Подставляем переменные в формулу:

Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.

При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например:

НЕЛЬЗЯ записать как:

Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:

Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x₁, x₂, …, x_n могут оказаться другие буквы. К примеру:

в матричной форме записываем так:

Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.

Решение матричных уравнений

Финальная глава саги.

Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».

Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.

Краткое содержание прошлых частей:

• Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
• Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
• Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
• Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
• Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
• Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.

И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.

❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.

Что такое матричное уравнение

Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.

Шаг 1. Упрощаем уравнение

Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.

Приводим матричное уравнение к упрощённому виду

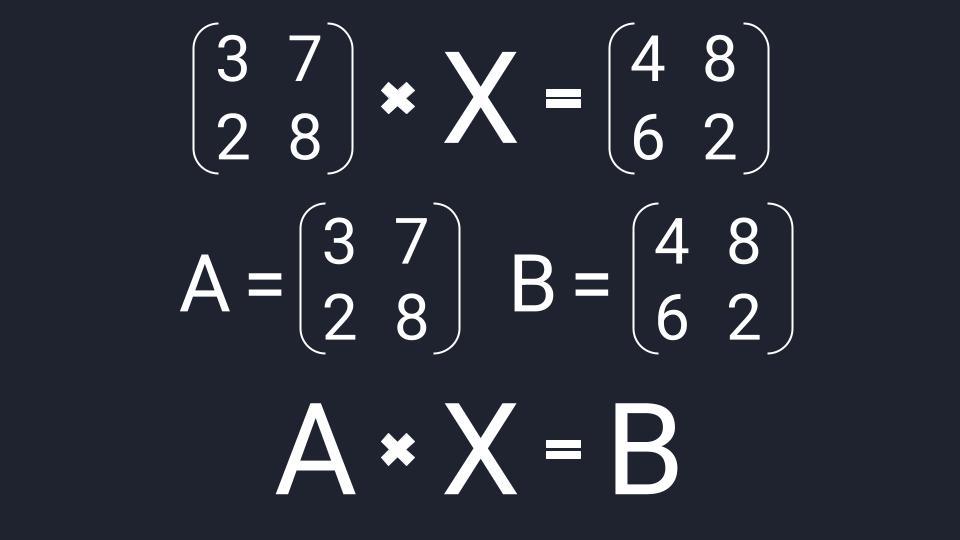
Шаг 2. Вводим единичную матрицу

В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.

Можно представить, что есть число 100 — это «сто в первой степени», 100 1

И есть число 0,01 — это «сто в минус первой степени», 100 -1

При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.

Вот такое, только в мире матриц.

Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:

А -1 × А × Х = А -1 × В

Добавляем единичную матрицу и упрощаем запись:

А -1 × А = E — единичная матрица

E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем

Х = А -1 × В — новая запись уравнения

После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.

💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.

Шаг 3. Находим обратную матрицу

Вспоминаем формулу и порядок расчёта обратной матрицы:

1. Делим единицу на определитель матрицы A.
2. Считаем транспонированную матрицу алгебраических дополнений.
3. Перемножаем значения и получаем нужную матрицу.

Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Третье действие: получаем обратную матрицу

Шаг 4. Вычисляем неизвестную матрицу

Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Решаем матричное уравнение и находим неизвестную матрицу X. Мы получили кратные числа и внесли дробь в матрицу

Шаг 5. Проверяем уравнение

Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.

👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Проверяем ответ и получаем матрицу B — наши расчёты верны

Ну и что

Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика: