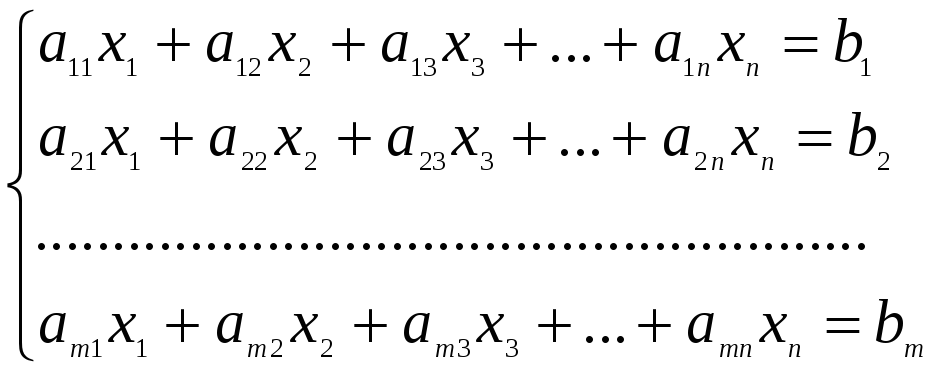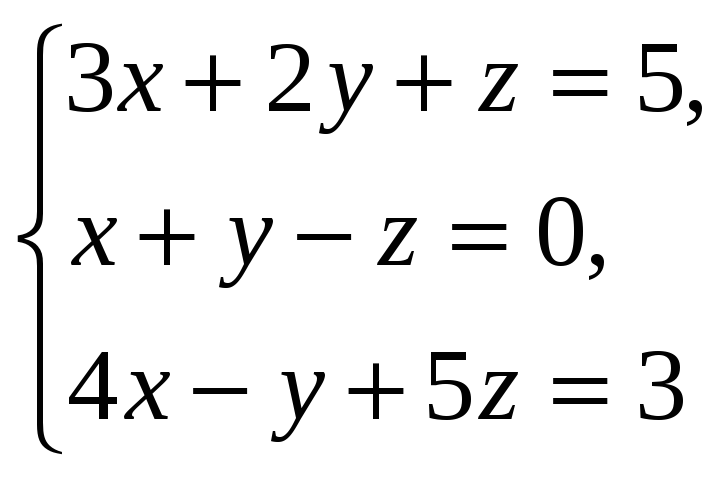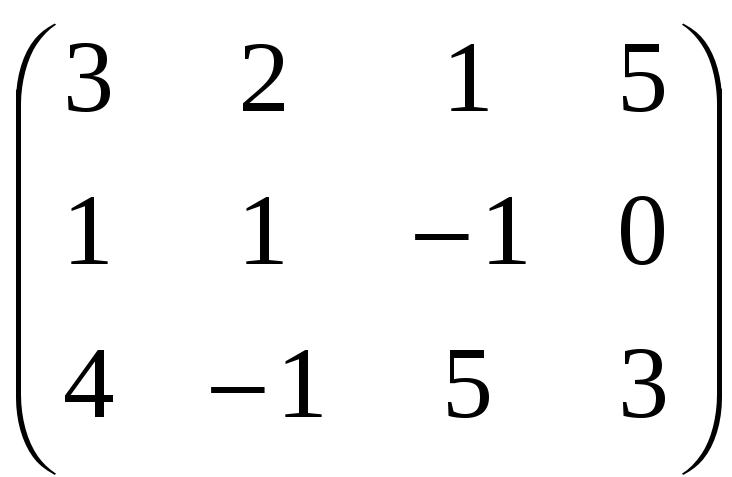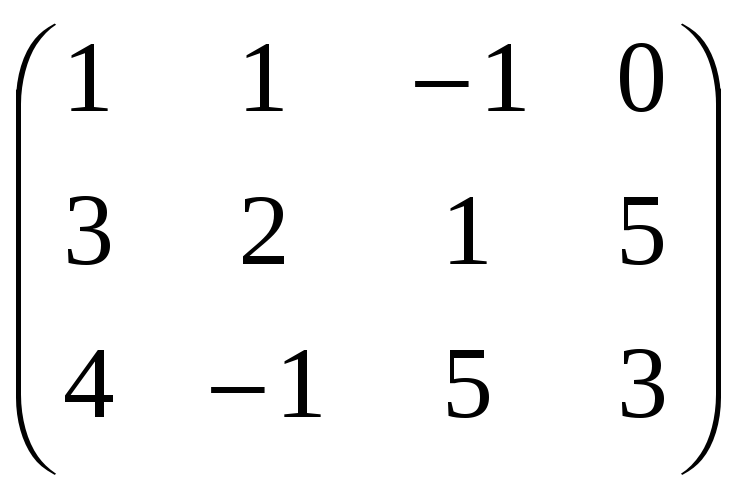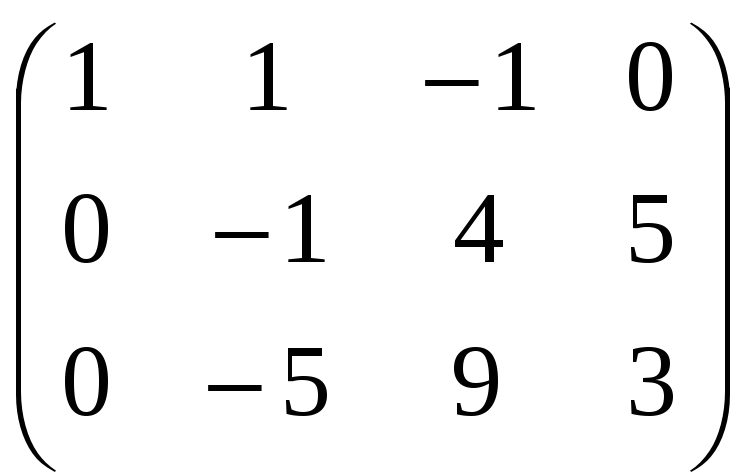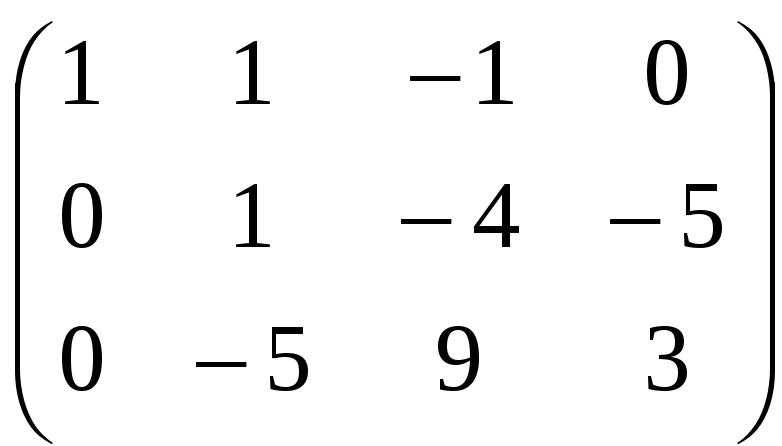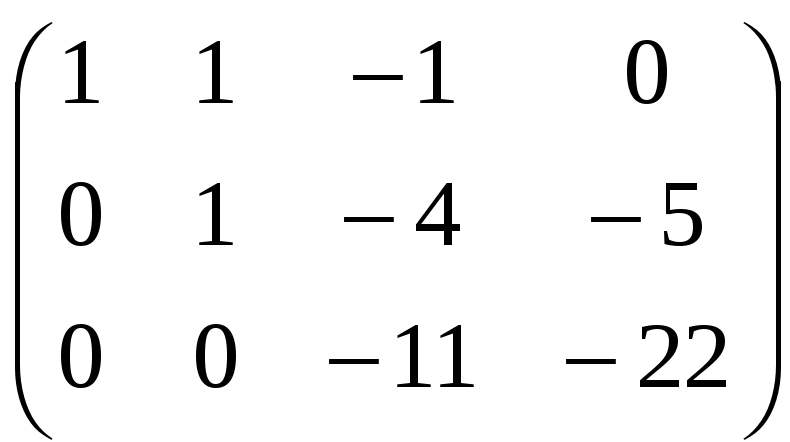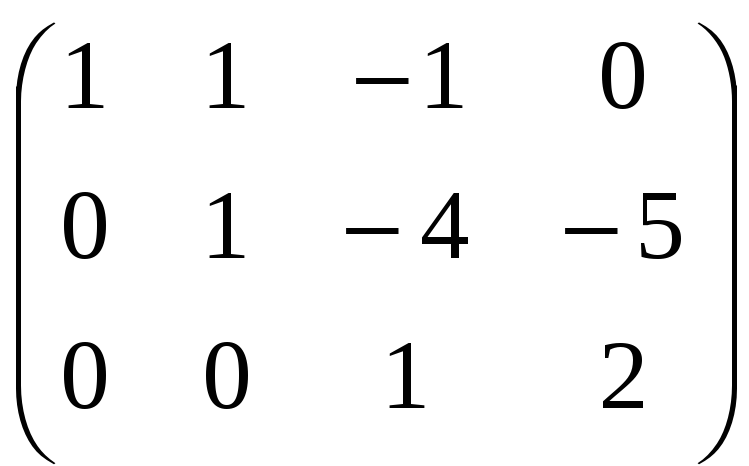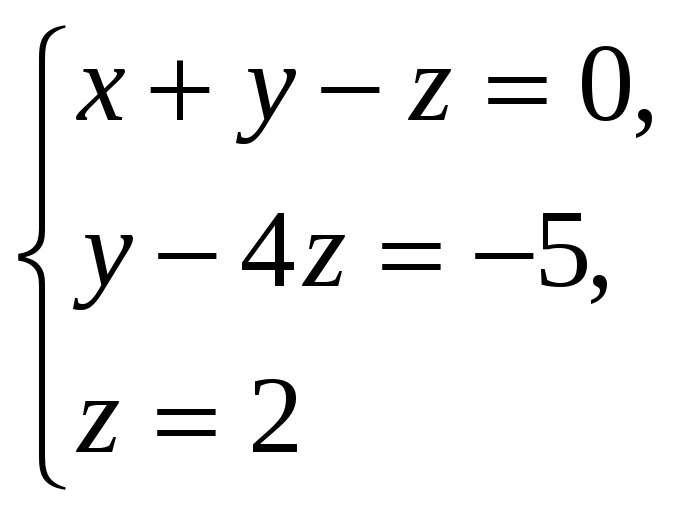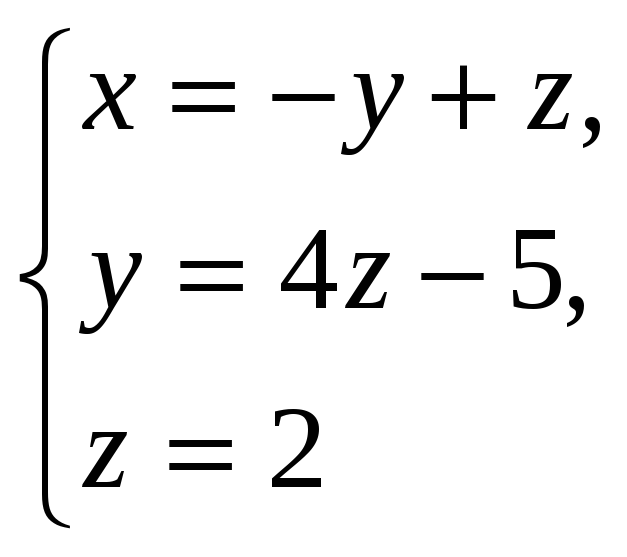Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.
С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).
Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: \( -2<,>34 \)
Ввод: -1,15
Результат: \( -1<,>15 \)
Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -\frac<2> <3>$$
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5\frac<8> <3>$$
Помните, что на ноль делить нельзя!
RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :
Немного теории.
Системы линейных алгебраических уравнений
Основные определения
Система \(m\) линейных алгебраических уравнений с \(n\) неизвестными (сокращенно СЛАУ) представляет собой систему вида
\( \left\< \begin
Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от \(n\) переменных \( x_1 , \ldots x_n \), а линейными потому, что эти многочлены имеют первую степень.
Числа \(a_
СЛАУ называют однородной, если \( b_1 = b_2 = \ldots = b_m = 0 \). Иначе её называют неоднородной.
Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных \( x_1^\circ, \ldots , x_n^\circ \), при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.
Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.
СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.
Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При \(m=n\), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.
Формы записи СЛАУ
Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.
Рассматривая коэффициенты \(a_
\( \begin
или, обозначая столбцы соответственно \( a_1 , \ldots , a_n , b \),
\( x_1 a_1 + x_2 a_2 + \ldots + x_n a_n = b \tag <2>\)
Таким образом, решение СЛАУ (1) можно трактовать как представление столбца \(b\) в виде линейной комбинации столбцов \( a_1, \ldots, a_n \). Соотношение (2) называют векторной записью СЛАУ.
Поскольку \(A \;,\; X\) и \(B\) являются матрицами, то запись СЛАУ (1) в виде \(AX=B\) называют матричной. Если \(B=0\), то СЛАУ является однородной и в матричной записи имеет вид \(AX=0\).
Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида \(AX=B\)
являются просто различной формой записи одной и той же задачи.
Критерий совместности СЛАУ
«Триединство» форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).
Матрицу
\( A = \begin
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
\( (A|B) = \left( \begin
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.
Теорема Кронекера-Капелли. Для совместности СЛАУ \(AX=B\) необходимо и достаточно, чтобы ранг её матрицы \(A\) был равен рангу её расширенной матрицы \( (A|B) \).
Формулы Крамера
Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = \frac<\Delta_i> <|A|>\;,\quad i=\overline <1,n>\tag <3>$$
где \(\Delta_i\) — определитель матрицы, получающейся из матрицы \(A\) заменой \(i\)-го столбца на столбец свободных членов.
Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.
Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.
Однородные системы
Теорема. Если столбцы \( X^<(1)>, X^<(2)>, \ldots , X^ <(s)>\) — решения однородной СЛАУ \(AX=0\), то любая их линейная комбинация также является решением этой системы.
Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.
Естественно попытаться найти такие решения \( X^<(1)>, \ldots , X^ <(s)>\) системы \(AX=0\), чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.
Определение. Любой набор из \(k=n-r\) линейно независимых столбцов, являющихся решениями однородной СЛАУ \(AX=0\), где \(n\) — количество неизвестных в системе, а \(r\) — ранг её матрицы \(A\), называют фундаментальной системой решений этой однородной СЛАУ.
При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице \(A\) однородной СЛАУ \(AX=0\) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.
Теорема. Пусть дана однородная СЛАУ \(AX=0\) с \(n\) неизвестными и \( \text
Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.
Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ <(1)>+ \ldots + c_kX^ <(k)>$$
где постоянные \( c_i \;, \quad i=\overline <1,k>\), принимают произвольные значения.
Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.
Неоднородные системы
Рассмотрим произвольную СЛАУ \(AX=B\). Заменив столбец \(B\) свободных членов нулевым, получим однородную СЛАУ \(AX=0\), соответствующую неоднородной СЛАУ \(AX=B\). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.
Теорема. Пусть столбец \(X^\circ\) — некоторое решение СЛАУ \(AX=B\). Произвольный столбец \(X\) является решением этой СЛАУ тогда и только тогда, когда он имеет представление \(X = X^\circ + Y \), где \(Y\) — решение соответствующей однородной СЛАУ \(AY=0\).
Следствие. Пусть \(X’\) и \(X»\) — решения неоднородной системы \(AX=B\). Тогда их разность \( Y = X’ — X» \) является решением соответствующей однородной системы \(AY=0\).
Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.
Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение \(X^\circ\) этой системы, чтобы свести её к однородной системе.
Теорема о структуре общего решения СЛАУ. Пусть \(X^\circ\) — частное решение СЛАУ \(AX=B\) и известна фундаментальная система решений \( X^<(1)>, \ldots , X^ <(k)>\) соответствующей однородной системы \(AX=0\). Тогда любое решение СЛАУ \(AX=B\) можно представить в виде $$ X = X^\circ + c_1 X^ <(1)>+ c_2 X^ <(2)>+ \ldots + c_k X^ <(k)>$$
где \( c_i \in \mathbb
Эту формулу называют общим решением СЛАУ.
Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Лекция 3. Понятие системы линейных уравнений. Метод Гаусса. Метод Крамера.
В данной лекции вводится понятие системы линейных алгебраических уравнений. Рассматриваются два метода решения СЛАУ: метод Крамера и метод Гаусса.
Просмотр содержимого документа
«Лекция 3. Понятие системы линейных уравнений. Метод Гаусса. Метод Крамера.»
Элементы линейной алгебры.
Лекция 3. Понятие СЛУ. Метод Гаусса. Метод Крамера
Лекция 3. Понятие системы линейных уравнений. Метод Гаусса. Метод Крамера.
1.1 Понятие системы линейных уравнений.
Определение 1. Системой линейных уравнений, содержащей m уравнений и n неизвестных, называется система вида
где числа aij – называются коэффициентами системы, числа bij – свободными членами.
Определение 2. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Определение 3. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
В последенем случае каждое решение системы называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему – это значит выяснить, совместна она или несовместна. Если совместна, найти ее общее решение.
1.2 Решение систем линейных уравнений. Метод Гаусса.
Пусть дана система m линейных уравнений с n неизвестными:
Матрица А = 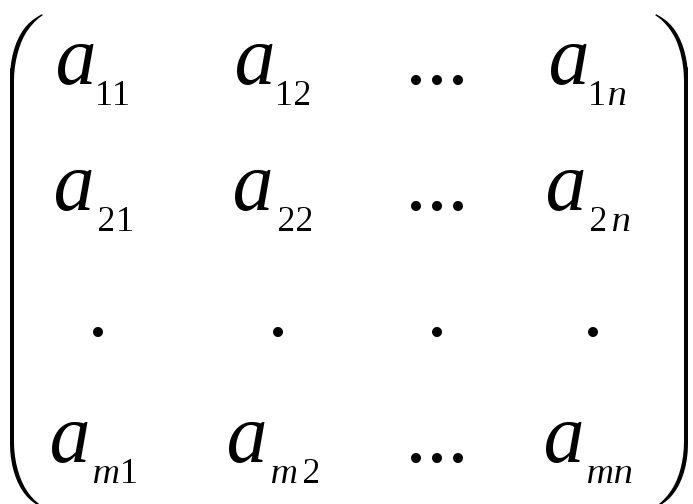
М
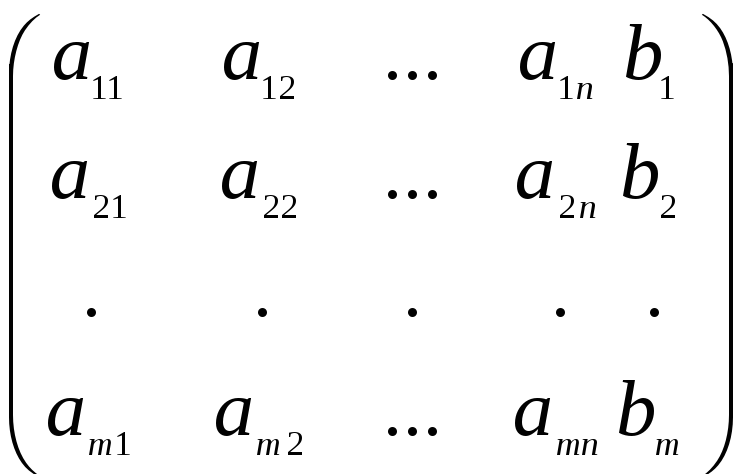
Определение 4. Матрица А называется матрицей треугольного вида, если все ее элементы выше (ниже) главной диагонали равны нулю.
Например, А = 
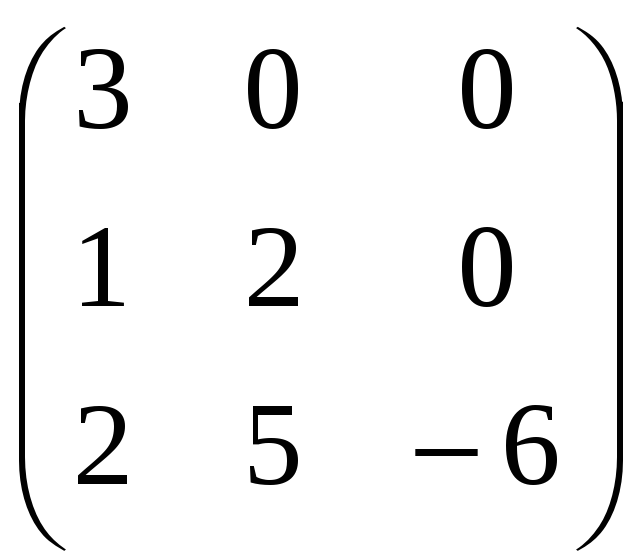
Метод Гаусса удобно использовать при решении систем с большим количеством уравнений. Этот метод заключается в последоваетльном исключении неизвестных. Систему линейных уравнений приводят к системе с треугольной матрицей с помощью эквивалентных преобразований. Затем из полученной системы переменные находят с помощью последовательных подстановок.
К эквивалентным преобразованиям относят следующие:
умножение и деление коэффициентов и свободных членов на одно и тоже число, отличное от нуля.
Сложение и вычитание уравнений.
Исключение из системы уравнений, в которых все коэффициенты равны нулю.
Решить систему линейных уравнений методом Гаусса:
Выпишем расширенную матрицу системы:
Для упрощения вычислений поменяем первую и вторую строки местами:
Умножим первую строку на –3 и сложим ее со второй строкой. Первую строку умножим на –4 и сложим с третьей сторокой, получим эквивалентную матрицу:
Умножим вторую строку на –1:
Умножим вторую строку на 5 и сложим с третьей строкой:
Разделим третью строку на –11:
Получили матрицу треугольного вида (все элементы ниже главной диагонали равны нулю). Выпишем систему уравнений треугольного вида:



Ответ: х = -1, у = 3, z = 2
1.3 Решение систем линейных уравнений методом Крамера.
Для решения систем линейных уравнений с большим количеством уравнений применяют метод Гаусса. Если же уравнений в системе не так много, то удобнее использовать метод Крамера. Этот метод основан на вычислении определителей.
Пусть дана система n линейных уравнений с n неизвестными:
Составим определитель матрицы системы:
Заменим в определителе первый столбик, соответствующий переменной х1, на столбец свободных членов b1, b2, …,bn, получим определитель х1:
Заменим в определителе второй столбик, соответствующий переменной х2, на столбец свободных членов b1, b2, …,bn, получим определитель х2:
Аналогично поступаем с третьим, четвертым, …, n –ым столбцами определителя . В итоге получим n+1 определитель. Для того, чтобы найти неизвестные х1, х2 , …, хn используем формулы Крамера:
При вычислении определителей могут возникнуть следующие случаи:
если определитель матрицы системы отличен от 0, то система линейных уравнений имеет единственное решение;
если определитель матрицы системы равен 0, а среди определителей х1, х2, …, хn есть хотя один отличный от 0, то система линейных уравнений не имеет решений;
если определитель матрицы системы равен 0 и все определители х1, х2, …, хn равны 0, то система линейных уравнений имеет бесконечно много решений.
Решить систему линейных уравнений методом Крамера:
Выпишем определитель матрицы системы и вычислим его:
Так как 0, то система имеет единственное решение.
Заменим в определителе первый столбик на столбец свободных коэффициентов, получим х :
Заменим в определителе второй столбик на столбец свободных коэффициентов, получим у :
Найдем значения переменных х и у по формулам Крамера:
Решить систему линейных уравнений методом Крамера:
Выпишем определитель матрицы системы и вычислим его:
Так как 0, то система имеет единственное решение.
Заменим в определителе первый столбик на столбец свободных коэффициентов, получим х :
Заменим в определителе первый столбик на столбец свободных коэффициентов, получим у :
Заменим в определителе первый столбик на столбец свободных коэффициентов, получим z :
Найдем значения переменных х , у и z по формулам Крамера:
http://www.evkova.org/metodyi-resheniya-sistem-linejnyih-algebraicheskih-uravnenij-slau
http://multiurok.ru/index.php/files/liektsiia-3-poniatiie-sistiemy-linieinykh-uravnien.html






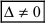 ), то система имеет единственное решение;
), то система имеет единственное решение;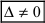 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 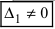 или
или 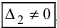 , или, . или
, или, . или 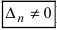 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);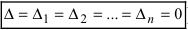 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.