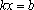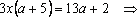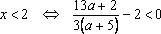Линейные уравнения параметрами 10 класс

Линейные уравнения с параметром

Рассмотрим линейные уравнения с параметром вида: $$p(a)x-q(a)=0,$$ где \(p(a)\) и \(q(a)\)- выражения, которые зависят от параметра. Для того, чтобы решить такое уравнение, нужно найти все \(x\) при всех значениях параметра \(a\). Приведем наше уравнение к виду: $$p(a)x=q(a),$$ Отсюда единственное решение: \(x=\frac\) при \(p(a)≠0.\) Если же \(p(a)=0\) и \(q(a)=0\), то решением данного уравнения является любое число. И последний случай, когда \(p(a)=0\),а \(q(a)≠0\), то уравнение не имеет решений. Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с \(x\) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились. Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:

Решить уравнение \(ax-5a=7x-3\) при всех возможных \(a\).

Перенесем все одночлены с \(x\) влево, а оставшиеся члены – вправо. И вынесем \(x\) за скобку, как общий множитель: $$x(a-7)=5a-3;$$ Первый случай, когда \((a-7)≠0\). Тогда мы можем поделить все уравнение на \(a-7\) и выразить: $$x=\frac<5a-3>.$$ Второй случай, когда \((a-7)=0\), получим уравнение $$x*0=32,$$ которое не имеет решений. Таким образом, мы нашли решения уравнения для всех значений параметра \(а\). Например, \(x=\frac<2><7>\) при \(a=0,\) \(x=\frac<-1><3>\) при \(a=1\) и т.д.
Ответ: При \(a=7\) \(x∈∅;\)
при \(a≠7\) \(x=\frac<5a-3>.\)

Найдите все \(a\), при которых корнем уравнения $$ax+5a-2(3x+2)=-5x+a^2$$ будет любое число.

Раскроем скобки и перенесем все члены, содержащие \(x\), влево, а остальные – вправо. $$ax-6x+5x=-5a+4+a^2$$ Приведем подобные: $$ax-x=a^2-5a+4$$ И вынесем за скобку \(x\) и разложим квадратный многочлен на множители: $$x(a-1)=a^2-5a+4$$ $$x(a-1)=(a-1)(a-4)$$ Первый случай: \((a-1)=0\),т.е. \(a=1\) $$x*0=(a-1)(a-4)$$ $$x*0=0.$$ Решением уравнения будет любое число.
Второй случай: \((a-1)≠0\), т.е. \(a≠1\) $$x=\frac<(a-1)(a-4)>=a-4.$$ Решением данного уравнения будет одно число \(x=a-4\).
Ответ: \(a=1.\)

Из ОДЗ видно, что \(5a+x≠0\) и \(x-5a≠0,\) таким образом, \(x≠±5a.\) Приведем уравнение к общему знаменателю \(x^2-25a^2\) и умножим на него все уравнение: $$x^2-5ax-x^2-10ax-25a^2=-100a^2$$ $$-15ax=-75a^2$$ $$ax=5a^2.$$

После преобразований получили линейное уравнение.

Первый случай: \(a=0.\) Получаем уравнение \(0*x=0.\) Решениями этого уравнения будет любое число, кроме \(x=0\) (ОДЗ \(x≠±5a\)).

Ответ: При \(a=0\) решениями уравнения будут все действительные числа, кроме \(x=0.\) Если \(a≠0,\) то решений нет.

Задачи с параметрами для 10-11 класса

Задачи с параметрами

(10 – 11 классы)

Параметры – это те же числа, просто заранее не известные.

1. Линейные уравнения и неравенства с параметрами

Линейная функция: — уравнение прямой с угловым коэффициентом . Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси .

Линейные уравнения с параметрами

Если , уравнение имеет единственное решение.

Если , то уравнение не имеет решений, когда , и уравнение имеет бесконечно много решений, когда .

Пример 1. При всех значениях параметра а решить уравнение: (a2 – 4)x = a + 2

Решение: Разложим коэффициент при на множители. .

Если , уравнение имеет единственное решение: .

Если , уравнение не имеет решений.

Если , то уравнение имеет бесконечно много решений .

Пример 2. При всех значениях параметра а решить уравнение: .

Решение: ОДЗ: . При этом условии уравнение равносильно следующему: . Проверим принадлежность к ОДЗ: , если . Если же , то уравнениене имеет решений.

Пример 3. При всех значениях параметра а решить уравнение:

Решение: Разобьем числовую прямую на 3 части точками, в которых выражения под знаком модуля обращаются в нуль и решим 3 системы:

1) , если . Найденный будет решением, если .

2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же

, то решением является любой .

3) , если . Найденный не удовлетворяет нужному неравенству, следовательно, не является решением при . Если же

, то решением является любой . Сформируем

Ответ: при ; при ;

при ; является также решением при всех .

Пример 4. Найти все а , при каждом из которых хотя бы одно из решений уравнения 15x – 7a = 2 – 3ax + 6a меньше 2 .

Решение: Найдем решения уравнения при каждом . , если . Решим неравенство:

При уравнение не имеет решений.

Ответ: а Î (-5, 4).

Линейные неравенства с параметрами

Пример 1. Решить неравенство:

Если , то . Если , то . Если , то при решением является любой , а при решений нет.

Аналогично решите остальные неравенства в рамочке.

Пример 2. Для всех значений параметра а решить неравенство

Решение. . Если скобка перед положительна, т.е. при , то . Если скобка перед отрицательна, т.е. при

, то . Если же или , то решений нет.

Пример 3. Для всех значений параметра а решить неравенство

Просмотр содержимого документа
«Задачи с параметрами для 10-11 класса »

Параметры – это те же числа, просто заранее не известные.

1. Линейные уравнения и неравенства с параметрами

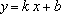
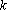
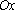
Линейная функция: — уравнение прямой с угловым коэффициентом . Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси .

Линейные уравнения с параметрами

Уравнение

Если 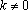, уравнение имеет единственное решение.

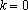
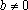
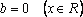
Если , то уравнение не имеет решений, когда , и уравнение имеет бесконечно много решений, когда .

Пример 1. При всех значениях параметра а решить уравнение: (a 2 – 4)x = a + 2

Решение: Разложим коэффициент при на множители. .

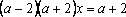
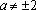
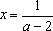
Если , уравнение имеет единственное решение: .

Если 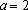, уравнение не имеет решений.

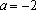
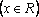
Если , то уравнение имеет бесконечно много решений .

Пример 2. При всех значениях параметра а решить уравнение: .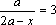

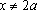
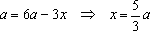
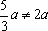
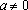
Решение: ОДЗ: . При этом условии уравнение равносильно следующему: . Проверим принадлежность к ОДЗ: , если . Если же , то уравнениене имеет решений.

Пример 3. При всех значениях параметра а решить уравнение:

Решение: Разобьем числовую прямую на 3 части точками, в которых выражения под знаком модуля обращаются в нуль и решим 3 системы:

1) , если . Найденный будет решением, если .

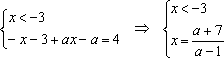
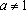
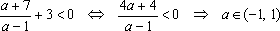
2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же

, то решением является любой .

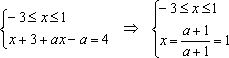
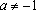
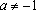
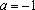
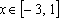
3) , если . Найденный не удовлетворяет нужному неравенству, следовательно, не является решением при . Если же

, то решением является любой . Сформируем

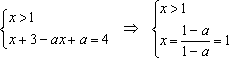
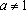
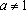
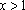
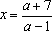
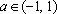
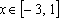
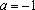
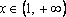
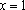
Ответ: при ; при ;

при ; является также решением при всех .

Пример 4. Найти все а , при каждом из которых хотя бы одно из решений уравнения 15x – 7a = 2 – 3ax + 6a меньше 2 .

Решение: Найдем решения уравнения при каждом . , если . Решим неравенство:

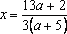
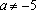
При уравнение не имеет решений.

Линейные неравенства с параметрами

Пример 1. Решить неравенство:

Если , то . Если , то . Если 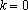, то при решением является любой , а при решений нет.

Аналогично решите остальные неравенства в рамочке.

Пример 2. Для всех значений параметра а решить неравенство

Решение. . Если скобка перед положительна, т.е. при , то . Если скобка перед отрицательна, т.е. при

, то . Если же или , то решений нет.

Пример 3. Для всех значений параметра а решить неравенство

Решение. При имеем неверное неравенство , т.е. решений нет. Пусть , тогда при оба модуля раскрываются с минусом и получаем неверное неравенство , т.е. решений нет. Если , то первый модуль раскрывается с минусом, а второй с плюсом и получаем неравенство , т.е. , т.е., решением является любой . Если оба модуля раскрываются с плюсом и получаем верное неравенство , т.е. , решением является любой . Объединяя оба ответа, получим, что при .

Пусть , тогда первое слагаемое больше, чем второе, поэтому разность в левой части неравенства положительна и, следовательно, не может быть меньше отрицательного числа . Т.о., при решений нет.

Ответ. При , при решений нет.

Замечание. Решении данной задачи получается быстрее и проще, если использовать геометрическую интерпретацию модуля разности двух чисел, как расстояние между точками. Тогда выражение в левой части можно интерпретировать, как разность расстояний от точки х до точек а и -а .

Пример 4. Найти все а , при каждом из которых все решения неравенства удовлетворяют неравенству .

Решение. Решением неравенства является множество , а решением неравенства является множество . Чтобы

удовлетворить условию задачи, нужно, чтобы множество А входило в множество В ( ). Это условие выполнится тогда и только тогда, когда

Пример 5. Найти все значения a , при которых неравенство выполняется для всех x из отрезка [1, 3] .

Решение. Дробь – меньше нуля между корнями, поэтому надо

выяснить, какой корень больше. и

. Т.о., при и чтобы неравенство выполнялось для всех x из отрезка [1, 3], нужно, чтобы

При и чтобы неравенство выполнялось для всех x из отрезка [1, 3], нужно, чтобы .

При (когда корни совпадают) решений нет, т.к. в этом случае неравенство приобретает вид : .

Пример 6. При каких значениях параметра а неравенство справедливо при всех отрицательных значениях х ?

Решение. Функция монотонно возрастает, если коэффициент при неотрицательный, и она монотонно убывает, если коэффициент при отрицательный.

Выясним знак коэффициента при . . .

Пусть . Тогда функция монотонно не убывает, и условие задачи будет выполнено, если

. Вместе с условиями получим : .

Пусть . Тогда функция монотонно убывает, и условие задачи никогда не может быть выполнено.

2. Векторы на плоскости

Пусть два вектора на плоскости заданы своими координатами:

Модуль (длина) вектора: .

где — угол между векторами.

Условие параллельности двух векторов: . Т.е.

у параллельных векторов координаты пропорциональны.

Условие перпендикулярности двух векторов: . Т.е. два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

Если вектор задан своими концами и , то вектор .

Задача 1. Через точку провести прямую, параллельную вектору .

Решение. Пусть точка — текущая точка искомой прямой. Тогда вектор параллелен вектору . Тогда выписывая условие параллельности, получим уравнение искомой прямой:

Переписав в виде , получим уравнение с угловым коэффициентом , проходящей через заданную точку .

Задача 2. Через точку провести прямую, перпендикулярную вектору . Вектор , перпендикулярный прямой, называется нормальным вектором к прямой илинормалью к прямой.

Решение. Пусть точка — текущая точка искомой прямой. Тогда вектор перпендикулярен вектору . Тогда выписывая условие перпендикулярности, получим уравнение искомой прямой:

Раскрыв скобки и обозначив число , получим так называемое общее уравнение прямой:

В этом уравнении коэффициенты при и являются координатами нормального вектора прямой.

Всякая прямая разбивает плоскость на две полуплоскости, где с одной стороны прямой и с другой стороны. При этом точки той

части плоскости, куда смотрит вектор , удовлетворяет неравенству . Поэтому:

В направлении вектора функция возрастает, а в направлении вектора она убывает.

Пример 5. Написать уравнение прямой, проходящей через точку параллельно прямой .

Решение. У параллельных прямых нормальные вектора тоже параллельны, т.е. . Согласно задаче 2 получим искомое уравнение: или .

3. Системы двух линейных уравнений с параметрами

Решениями системы двух линейных уравнений являются точки пересечения двух прямых: и .

Возможны 3 случая:

1. Прямые не параллельны . Тогда и их нормальные вектора не параллельны, т.е. . В этом случае система имеет единственное решение.

2. Прямые параллельны и не совпадают. Тогда и их нормальные вектора параллельны, но сдвиги различны, т.е. .

В этом случае система решений не имеет .

3. Прямые совпадают. Тогда их нормальные вектора параллельны и сдвиги совпадают, т.е. . В этом случае система имеет бесконечно много решений – все точки прямой.

Пример 1. При всех значениях а и b решить систему уравнений

Решение. Выразим из первого уравнения и подставим во второе уравнение. Получим: .

Если — единственное решение. Если , то если , то решений бесконечно много: . Если

же , то решений нет.

Пример 2. При каком значении параметра а система уравнений

Решение. Система не имеет решений, если .

Пример 3. При всех значениях а решить систему уравнений

Решение. Система равносильна совокупности двух систем:

Прямые параллельны , если . При этом прямые не совпадают, поэтому при 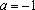решений нет.

Если 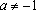, то выражая из второго уравнения и подставляя в первое, получим: .

Пример 4. Найти все такие значения а, что для любого значения b

найдётся хотя бы одно с такое, что система уравнений

имеет хотя бы одно решение.

Решение. Прямые не параллельны, если

В этом случае система имеет единственное решение при любом c.

По условию задачи система должна иметь решение при всех b.

Если то система принимает вид: . Чтобы при система также имела решения, нужно, чтобы уравнение относительно c имело хотя бы одно решение. Т.о., дискриминант этого уравнения должен быть неотрицательным, т.е.

Аналогично, если то система принимает вид: Чтобы при система также имела решения, нужно, чтобы уравнение

относительно c имело хотя бы одно решение. Т.о., дискриминант этого уравнения должен быть неотрицательным, т.е.

4. Системы двух линейных неравенств с параметрами

Пример 1. При каких значениях а система неравенств

не имеет решений?

Решение. Система имеет решения только если .

Ответ: при решением будет любой ;

при решений нет.

Пример 2. При каких значениях а система неравенств

имеет хотя бы одно решение?

Решение. При первое неравенство не имеет решений. А тогда и вся система не имеет решений.

Пусть , тогда и эта система не имеет решений, так как , а . Пусть , тогда т.е.

решения есть при , и , так как при выполнено неравенство , то решение запишется в виде .

Ответ: при решением будет любой ;

при решений нет.

Пример 3. При всех значениях а решить систему

Решение. Перепишем систему неравенств в виде . Рассмотрим все возможные случаи.

1) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем: при

2) . Тогда первое неравенство не верно. А значит, и вся система не имеет решений .

3) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем:

4) . Тогда второе неравенство не верно. А значит, и вся система не имеет решений .

5) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем: при

при и при решений нет.

Пример 4. При всех значениях а решить систему

При система не имеет решений.

Пусть , тогда и эта система не имеет решений.

Пусть , тогда и эта система будет иметь решения, если выполнено неравенство: .

Урок по теме: Решение линейных уравнений и неравенств с параметрами в 10 классе.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Урок в 10 классе

«Решение линейных уравнений и неравенств с параметрами».

Выполнила: Галстян Г.С.

Учитель математики МОУ «СОШ №11»

Конспект урока в 10 классе

Тема урока: «Решение линейных уравнений и неравенств с параметрами».

Цель: — повторить, закрепить и привести в систему знания и умения решать линейные уравнения и неравенства с параметрами, полученные в 9 классе;

-развивать логическое мышление, математическую речь, интерес к изучению математики;

— воспитывать аккуратность. Взаимопонимание. (слайд 2)

Форма работы: фронтальная беседа, работа в парах.

Метод работы: — методы организации учебно-познавательной деятельности: наглядные, практические, исследовательские;

— методы стимулирования и мотивации учебно-познавательной деятельности: учебная дискуссия, эмоциональное воздействие;

-методы контроля: письменный, самопроверка.

Оборудование: проектор, карточки.

Литература: Учебник 10-11 класса «Алгебра и начала анализа 10-11» Мордкович А.Г. – изд. Мнемозина, 2012г, задачник 10-11 класса «Алгебра и начала анализа 10-11» Мордкович А.Г. – изд. Мнемозина, 2012г.

I .Организационный момент.

II .Актуализация знаний.

У. Обычно в уравнении или неравенстве буквами обозначаются переменные.

У. Что значит решить уравнение или неравенство?

ОТВ. Решить уравнение или неравенство означает найти множество значений неизвестных, удовлетворяющих этому уравнению или неравенству.

У. Иногда уравнения и неравенства, кроме букв, обозначающих неизвестные, содержат другие буквы, называемые параметрами.

Определение. Переменная, значение которой на протяжении некоторого контекста остается фиксированным, называется параметром, по отношению к этому контексту. (слайд3)

Когда предлагают решить уравнение или неравенство с параметрами, тем самым указывают, что переменные, названные параметрами, должны рассматриваться как произвольные, но фиксированные коэффициенты.

Предавая параметрам разные числовые значения, получаем различные уравнения или неравенства, например, в линейном уравнении ax + b =0 или неравенстве ax + b ≥0,

x — переменная, a и b — параметры.

При решении уравнений или неравенств надо сначала найти множество допустимых значений параметров, а затем разбить это множество на части, в каждом из которых ответ выражается функцией через параметры.

Определение. Множество значений параметра, при каждом из которых или существуют в области действительных чисел, называют областью допустимых значений параметра. (слайд 4)

Пример 1. Данное уравнение имеет смысл при

Пример 2.× x ≤2 a – имеет смысл при a ≥3.

Определение. Число называют допустимым значением переменной x , если f и g действительны при каждом допустимом значении параметра.

Определение. Областью определения неравенства (уравнения) множества всех допустимых значений x , при которых уравнение (неравенство) имеет смысл.

В примере 1. x , в примере 2. x .(слайд 5)

Вспомним решение линейных уравнений и неравенств с параметрами a и b .

Если a – единственный корень.

Если a =0, b =0, то 0 x =0, — уравнение имеет множество корней.

Если a =0, b 0 x = b – уравнение корней не имеет.

1.Если a неравенство имеет множество решений. Если , то неравенство решений не имеет.

III . Закрепление теоретических навыков.

Решают у доски по карточкам.

№ 1. Решить уравнение относительно x .

a =-3, уравнение корней не имеет;

Ответ: а) а= -3, уравнение корней не имеет; б) , то .

№ 2. Решить неравенство относительно x .

Для самостоятельного решения с последующей проверкой ответов.

а х – 3=х+2. Ответ: а=1, нет корней; а .

ах – 3 х +2. Ответ: а=1, нет решений; а1, х ; а1 , х.(слайд 6)

IV .Исследовательская деятельность. (работа в парах)

Решите уравнение и неравенство с параметром задачник № 60.1; № 60,3; № 60.4(б).

№ 60.1 При каких значениях параметра m уравнение mx – x + 1= :

а) имеет ровно один корень;

б) не имеет корней;

в) имеет более одного корня?

в) m = 1, 0 x = 0, х- любое число.

Ответ: а) m 1, x =; б) таких m нет; в) m = 1, 0 x = 0, х- любое число.

№ 60.3 Решение уравнение (относительно х):

а = 2, а — 2; 0х = 0, х – любое число.

а = — 2, а = 2, а — 2, 0х = — 4, решений нет.

Ответ: а = 2, а — 2; 0х = 0, х – любое число; а = — 2, а = 2, а — 2, 0х = — 4, решений нет; а — 2, а 2, х = .

а = — 1, а 0, 0х = 0, х – любое число;

а 0, а — 1, х =, х = а;

Ответ: а = — 1, а 0, 0х = 0, х – любое число; а 0, а — 1, х = а; а =0, корней нет.

№ 60.4 (а) Решите неравенство (относительно х):

m = 1, 0 x 0, х – любое число;

Ответ: m = 1, 0x ≥ 0, х – любое число; m ≠ 1, m >1, x ≥ m +1; m ≠ 1, m

Сегодня на уроке мы повторили решение линейных уравнений и неравенств с параметрами. На следующем уроке мы будем рассматривать решение квадратных уравнений и неравенств с параметрами.

VI. Домашнее задание. (слайд 7)

Повторить решение квадратных уравнений и неравенств;

Учебник с.383 параграф 60 (до примера 2) – прочитать;