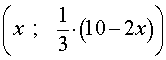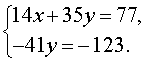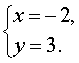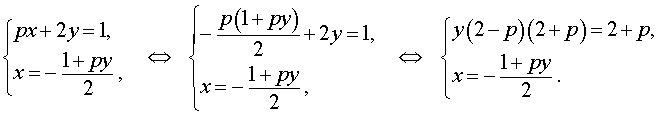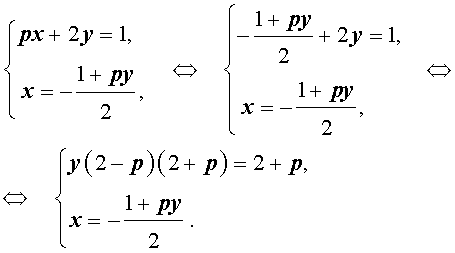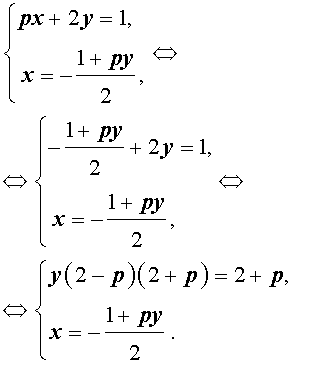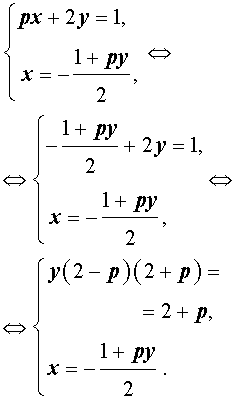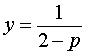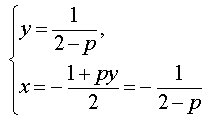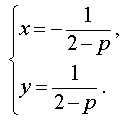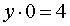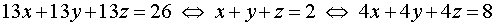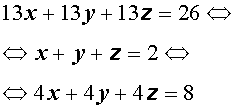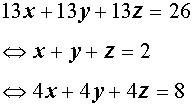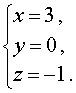Математика
63. Два уравнения с тремя неизвестными . Пусть имеем уравнения:
3x + 4y – 2z = 11
5x + 4y + 2z = 19,
которые надо решить совместно. Мы умеем решать совместно 2 уравнения с двумя неизвестными, почему прежде всего приходит мысль, что здесь одно неизвестное является лишним и что его, вероятно, можно заменить любым числом. И действительно. Если дадим x произвольное значение, например, возьмем x = 7, то получим
21 + 4y – 2z = 11
35 + 4y + 2z = 19,
т. е. 2 уравнения с двумя неизвестными, которые мы умеем решить.
Упростив эти уравнения, получим:
4y – 2z = –10
4y + 2z = –16.
Сложив из по частям, получим:
Вычитая из 2-го первое, получим:
Взяв x = 0, получим:
4y – 2z = 11
4y + 2z = 19.
Решив (так же, как и выше) эти уравнения, получим:
Так же для x = 1, получим y = 2 ¾; z = 1 ½ и т. д.
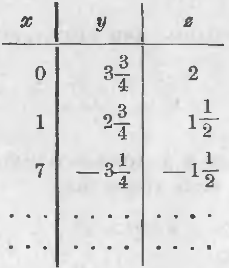
Эти решения можно записать в таблице, причем, как видим, здесь одно неизвестное (у нас x) является независимым переменным, а два других являются зависимыми переменными.
Вот эта таблица:
два уравнения с тремя неизвестными имеют бесконечно много решений, причем для получения их надо одному из неизвестных давать произвольные значения .
Чтобы удобнее получать эти решения, можно заранее из данных уравнений определить зависимые переменные через независимое.
Для этой цели перенесем члены 3x и 5x, имеющиеся в наших уравнениях, в правую часть (эти члены, ведь, приходится считать известными), — получим:
4y – 2z = 11 – 3x
4y + 2z = 19 – 5x.
Сложив эти уравнения по частям, получим:
8y = 30 – 8x и y = (30 – 8x) / 8 = (15 – 4x) / 4.
Вычитая по частям из 2-го уравнения первое, получим:
4z = 8 – 2x и z = (8 – 2x) / 4 = (4 – x) / 2.
Теперь, взяв для x какое-нибудь значение, например, x = 2, легко в уме найдем: y = 1 ¾ и z = 1.
Вот еще пример. Пусть даны уравнения:
2x + y – z = 7
3x + 2y + 4z = 11.
Определим из них x и y через z. Для этого сначала перенесем члены с z в правую часть уравнения:
2x + y = 7 + z и 3x + 2y = 11 – 4z (1).
Обе части первого уравнения умножим на 2:
4x + 2y = 14 + 2z
3x + 2y = 11 – 4z.
Вычтем по частям из 1-го уравнения второе:
Таким образом мы определили x через z. Затем умножим обе части 1-го уравнения из системы (1) на 3 и обе части 2-го на 2 (чтобы уравнять коэффициенты при x). Получим:
6x + 3y = 21 + 3z
6x + 4y = 22 – 8z.
Вычитая по частям из 2-го уравнения первое, получим:
Таким образом определили y через z.
Пользуясь равенствами (2) и (3), легко найти сколько угодно решений данных двух уравнений, причем надо неизвестному z давать произвольные значения. Вот несколько решений:
Системы линейных уравнений
 Линейные уравнения (уравнения первой степени) с двумя неизвестными Линейные уравнения (уравнения первой степени) с двумя неизвестными |
 Системы из двух линейных уравнений с двумя неизвестными Системы из двух линейных уравнений с двумя неизвестными |
 Системы из трех линейных уравнений с тремя неизвестными Системы из трех линейных уравнений с тремя неизвестными |
Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
| ax +by = c , | (1) |
где a , b , c – заданные числа.
Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1 . Найти решение уравнения
| 2x +3y = 10 | (2) |
Решение . Выразим из равенства (2) переменную y через переменную x :
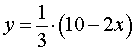 | (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Системы из двух линейных уравнений с двумя неизвестными
Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
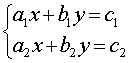 | (4) |
Определение 4 . В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных , а числа c1 , c2 – свободными членами .
Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
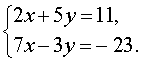 | (5) |
Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
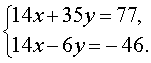 | (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Пример 3 . Найти все значения параметра p , при которых система уравнений
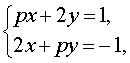 | (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
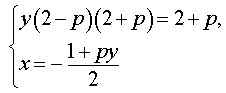 | (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если 
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда 
Если p = – 2 , то уравнение (9) принимает вид
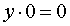
и его решением является любое число 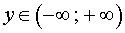
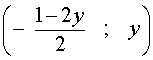
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Системы из трех линейных уравнений с тремя неизвестными
Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
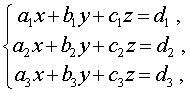 | (10) |
Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
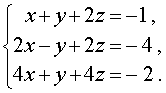 | (11) |
Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
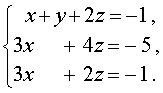 | (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
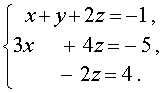 | (13) |
Из системы (13) последовательно находим
Пример 5 . Решить систему уравнений
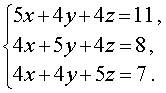 | (14) |
Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
Линейные уравнения и системы линейных уравнений
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
В данном уроке мы рассмотрим линейные уравнения и системы линейных уравнений с двумя и тремя переменными.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства»
http://www.resolventa.ru/spr/algebra/system.htm
http://interneturok.ru/lesson/algebra/11-klass/povtorenie/lineynye-uravneniya-i-sistemy-lineynyh-uravneniy