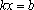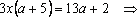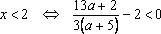Линейные уравнения с параметрами 10 класс примеры

Линейные уравнения с параметром

Рассмотрим линейные уравнения с параметром вида: $$p(a)x-q(a)=0,$$ где \(p(a)\) и \(q(a)\)- выражения, которые зависят от параметра. Для того, чтобы решить такое уравнение, нужно найти все \(x\) при всех значениях параметра \(a\). Приведем наше уравнение к виду: $$p(a)x=q(a),$$ Отсюда единственное решение: \(x=\frac\) при \(p(a)≠0.\) Если же \(p(a)=0\) и \(q(a)=0\), то решением данного уравнения является любое число. И последний случай, когда \(p(a)=0\),а \(q(a)≠0\), то уравнение не имеет решений. Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с \(x\) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились. Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:

Решить уравнение \(ax-5a=7x-3\) при всех возможных \(a\).

Перенесем все одночлены с \(x\) влево, а оставшиеся члены – вправо. И вынесем \(x\) за скобку, как общий множитель: $$x(a-7)=5a-3;$$ Первый случай, когда \((a-7)≠0\). Тогда мы можем поделить все уравнение на \(a-7\) и выразить: $$x=\frac<5a-3>.$$ Второй случай, когда \((a-7)=0\), получим уравнение $$x*0=32,$$ которое не имеет решений. Таким образом, мы нашли решения уравнения для всех значений параметра \(а\). Например, \(x=\frac<2><7>\) при \(a=0,\) \(x=\frac<-1><3>\) при \(a=1\) и т.д.
Ответ: При \(a=7\) \(x∈∅;\)
при \(a≠7\) \(x=\frac<5a-3>.\)

Найдите все \(a\), при которых корнем уравнения $$ax+5a-2(3x+2)=-5x+a^2$$ будет любое число.

Раскроем скобки и перенесем все члены, содержащие \(x\), влево, а остальные – вправо. $$ax-6x+5x=-5a+4+a^2$$ Приведем подобные: $$ax-x=a^2-5a+4$$ И вынесем за скобку \(x\) и разложим квадратный многочлен на множители: $$x(a-1)=a^2-5a+4$$ $$x(a-1)=(a-1)(a-4)$$ Первый случай: \((a-1)=0\),т.е. \(a=1\) $$x*0=(a-1)(a-4)$$ $$x*0=0.$$ Решением уравнения будет любое число.
Второй случай: \((a-1)≠0\), т.е. \(a≠1\) $$x=\frac<(a-1)(a-4)>=a-4.$$ Решением данного уравнения будет одно число \(x=a-4\).
Ответ: \(a=1.\)

Из ОДЗ видно, что \(5a+x≠0\) и \(x-5a≠0,\) таким образом, \(x≠±5a.\) Приведем уравнение к общему знаменателю \(x^2-25a^2\) и умножим на него все уравнение: $$x^2-5ax-x^2-10ax-25a^2=-100a^2$$ $$-15ax=-75a^2$$ $$ax=5a^2.$$

После преобразований получили линейное уравнение.

Первый случай: \(a=0.\) Получаем уравнение \(0*x=0.\) Решениями этого уравнения будет любое число, кроме \(x=0\) (ОДЗ \(x≠±5a\)).

Ответ: При \(a=0\) решениями уравнения будут все действительные числа, кроме \(x=0.\) Если \(a≠0,\) то решений нет.

Уравнения с параметром

Разделы: Математика

Справочный материал

Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.

Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет

Если 1 – а 0, т.е. а 1, то х =

Пример 4.

Если а = 1, то 0х = 0
х – любое действительное число

Если а = -1, то 0х = -2
Корней нет

Если а 1, а -1, то х = (единственное решение).

Это значит, что каждому допустимому значению а соответствует единственное значение х.

если а = 5, то х = = ;

Дидактический материал

3. а = +

4. + 3(х+1)

5. = –

6. =

Ответы:

1. При а1 х =;

1. При а3 х = ;

1. При а1, а-1, а0 х = ;

при а = 1 х – любое действительное число, кроме х = 1

1. При а2, а0 х = ;

1. При а-3, а-2, а0, 5 х =

1. При а + с0, с0 х = ;

Квадратные уравнения с параметром

Пример 1. Решить уравнение

х = –

В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.

Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16

a =

a =

Если а -4/5 и а 1, то Д > 0,

х =

х = – = –

Пример 2. При каких значениях параметра а уравнение

х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?

В итоге

4(а – 1)(а – 6) > 0 — 2(а + 1) 0

а 6 а > — 1 а > 5/9

6

Пример 3. Найдите значения а, при которых данное уравнение имеет решение.

Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а

4а 2 – 16 0

4а(а – 4) 0

а(а – 4)) 0

Ответ: а 0 и а 4

Дидактический материал

1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?

2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?

3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?

4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?

5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?

Показательные уравнения с параметром

Пример 1.Найти все значения а, при которых уравнение

9 х – (а + 2)*3 х-1/х +2а*3 -2/х = 0 (1) имеет ровно два корня.

Решение. Умножив обе части уравнения (1) на 3 2/х , получим равносильное уравнение

3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)

Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или

Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log₃2 , или х 2 – хlog₃2 + 1 = 0.

Это уравнение не имеет действительных корней, так как его Д = log 2 ₃2 – 4 х+1/х = а то х + 1/х = log₃а, или х 2 – хlog₃а + 1 = 0. (3)

Уравнение (3) имеет ровно два корня тогда и только тогда, когда

Д = log 2 ₃2 – 4 > 0, или |log₃а| > 2.

Если log₃а > 2, то а > 9, а если log₃а 9.

Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?

Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х₁ = -3, х₂ = а = >

а – положительное число.

Дидактический материал

1. Найти все значения а, при которых уравнение

25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.

2. При каких значениях а уравнение

2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?

3. При каких значениях параметра а уравнение

4 х — (5а-3)2 х +4а 2 – 3а = 0 имеет единственное решение?

Ответ:

1. 0 25/2
2. при а = 1, а = -2,2
3. 0 0, х1/4 (3)

х = у

Если а = 0, то –

2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4

Не выполняется (2) условие из (3).

Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.

Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).

Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х

Выражая х из (1) и подставляя в (2), получаем неравенство

2 – а > 1 – а (3)

Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.

Решения неравенства (3) образуют промежуток (а₀; 2), где а₀ 2

а₀ =

Ответ: x + 9a 3 ) = x имеет ровно два корня.

Ответы:

при а 16.06.2009

Задачи с параметрами для 10-11 класса

Задачи с параметрами

(10 – 11 классы)

Параметры – это те же числа, просто заранее не известные.

1. Линейные уравнения и неравенства с параметрами

Линейная функция: — уравнение прямой с угловым коэффициентом . Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси .

Линейные уравнения с параметрами

Если , уравнение имеет единственное решение.

Если , то уравнение не имеет решений, когда , и уравнение имеет бесконечно много решений, когда .

Пример 1. При всех значениях параметра а решить уравнение: (a2 – 4)x = a + 2

Решение: Разложим коэффициент при на множители. .

Если , уравнение имеет единственное решение: .

Если , уравнение не имеет решений.

Если , то уравнение имеет бесконечно много решений .

Пример 2. При всех значениях параметра а решить уравнение: .

Решение: ОДЗ: . При этом условии уравнение равносильно следующему: . Проверим принадлежность к ОДЗ: , если . Если же , то уравнениене имеет решений.

Пример 3. При всех значениях параметра а решить уравнение:

Решение: Разобьем числовую прямую на 3 части точками, в которых выражения под знаком модуля обращаются в нуль и решим 3 системы:

1) , если . Найденный будет решением, если .

2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же

, то решением является любой .

3) , если . Найденный не удовлетворяет нужному неравенству, следовательно, не является решением при . Если же

, то решением является любой . Сформируем

Ответ: при ; при ;

при ; является также решением при всех .

Пример 4. Найти все а , при каждом из которых хотя бы одно из решений уравнения 15x – 7a = 2 – 3ax + 6a меньше 2 .

Решение: Найдем решения уравнения при каждом . , если . Решим неравенство:

При уравнение не имеет решений.

Ответ: а Î (-5, 4).

Линейные неравенства с параметрами

Пример 1. Решить неравенство:

Если , то . Если , то . Если , то при решением является любой , а при решений нет.

Аналогично решите остальные неравенства в рамочке.

Пример 2. Для всех значений параметра а решить неравенство

Решение. . Если скобка перед положительна, т.е. при , то . Если скобка перед отрицательна, т.е. при

, то . Если же или , то решений нет.

Пример 3. Для всех значений параметра а решить неравенство

Просмотр содержимого документа
«Задачи с параметрами для 10-11 класса »

Параметры – это те же числа, просто заранее не известные.

1. Линейные уравнения и неравенства с параметрами

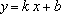
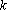
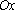
Линейная функция: — уравнение прямой с угловым коэффициентом . Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси .

Линейные уравнения с параметрами

Уравнение

Если 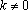, уравнение имеет единственное решение.

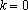
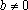
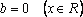
Если , то уравнение не имеет решений, когда , и уравнение имеет бесконечно много решений, когда .

Пример 1. При всех значениях параметра а решить уравнение: (a 2 – 4)x = a + 2

Решение: Разложим коэффициент при на множители. .

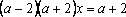
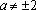
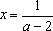
Если , уравнение имеет единственное решение: .

Если 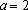, уравнение не имеет решений.

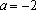
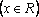
Если , то уравнение имеет бесконечно много решений .

Пример 2. При всех значениях параметра а решить уравнение: .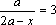

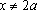
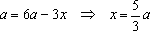
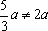
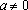
Решение: ОДЗ: . При этом условии уравнение равносильно следующему: . Проверим принадлежность к ОДЗ: , если . Если же , то уравнениене имеет решений.

Пример 3. При всех значениях параметра а решить уравнение:

Решение: Разобьем числовую прямую на 3 части точками, в которых выражения под знаком модуля обращаются в нуль и решим 3 системы:

1) , если . Найденный будет решением, если .

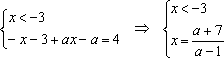
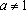
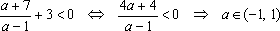
2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же

, то решением является любой .

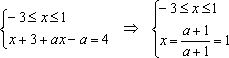
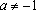
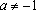
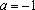
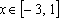
3) , если . Найденный не удовлетворяет нужному неравенству, следовательно, не является решением при . Если же

, то решением является любой . Сформируем

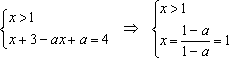
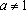
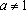
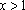
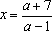
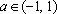
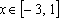
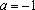
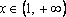
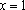
Ответ: при ; при ;

при ; является также решением при всех .

Пример 4. Найти все а , при каждом из которых хотя бы одно из решений уравнения 15x – 7a = 2 – 3ax + 6a меньше 2 .

Решение: Найдем решения уравнения при каждом . , если . Решим неравенство:

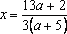
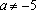
При уравнение не имеет решений.

Линейные неравенства с параметрами

Пример 1. Решить неравенство:

Если , то . Если , то . Если 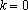, то при решением является любой , а при решений нет.

Аналогично решите остальные неравенства в рамочке.

Пример 2. Для всех значений параметра а решить неравенство

Решение. . Если скобка перед положительна, т.е. при , то . Если скобка перед отрицательна, т.е. при

, то . Если же или , то решений нет.

Пример 3. Для всех значений параметра а решить неравенство

Решение. При имеем неверное неравенство , т.е. решений нет. Пусть , тогда при оба модуля раскрываются с минусом и получаем неверное неравенство , т.е. решений нет. Если , то первый модуль раскрывается с минусом, а второй с плюсом и получаем неравенство , т.е. , т.е., решением является любой . Если оба модуля раскрываются с плюсом и получаем верное неравенство , т.е. , решением является любой . Объединяя оба ответа, получим, что при .

Пусть , тогда первое слагаемое больше, чем второе, поэтому разность в левой части неравенства положительна и, следовательно, не может быть меньше отрицательного числа . Т.о., при решений нет.

Ответ. При , при решений нет.

Замечание. Решении данной задачи получается быстрее и проще, если использовать геометрическую интерпретацию модуля разности двух чисел, как расстояние между точками. Тогда выражение в левой части можно интерпретировать, как разность расстояний от точки х до точек а и -а .

Пример 4. Найти все а , при каждом из которых все решения неравенства удовлетворяют неравенству .

Решение. Решением неравенства является множество , а решением неравенства является множество . Чтобы

удовлетворить условию задачи, нужно, чтобы множество А входило в множество В ( ). Это условие выполнится тогда и только тогда, когда

Пример 5. Найти все значения a , при которых неравенство выполняется для всех x из отрезка [1, 3] .

Решение. Дробь – меньше нуля между корнями, поэтому надо

выяснить, какой корень больше. и

. Т.о., при и чтобы неравенство выполнялось для всех x из отрезка [1, 3], нужно, чтобы

При и чтобы неравенство выполнялось для всех x из отрезка [1, 3], нужно, чтобы .

При (когда корни совпадают) решений нет, т.к. в этом случае неравенство приобретает вид : .

Пример 6. При каких значениях параметра а неравенство справедливо при всех отрицательных значениях х ?

Решение. Функция монотонно возрастает, если коэффициент при неотрицательный, и она монотонно убывает, если коэффициент при отрицательный.

Выясним знак коэффициента при . . .

Пусть . Тогда функция монотонно не убывает, и условие задачи будет выполнено, если

. Вместе с условиями получим : .

Пусть . Тогда функция монотонно убывает, и условие задачи никогда не может быть выполнено.

2. Векторы на плоскости

Пусть два вектора на плоскости заданы своими координатами:

Модуль (длина) вектора: .

где — угол между векторами.

Условие параллельности двух векторов: . Т.е.

у параллельных векторов координаты пропорциональны.

Условие перпендикулярности двух векторов: . Т.е. два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

Если вектор задан своими концами и , то вектор .

Задача 1. Через точку провести прямую, параллельную вектору .

Решение. Пусть точка — текущая точка искомой прямой. Тогда вектор параллелен вектору . Тогда выписывая условие параллельности, получим уравнение искомой прямой:

Переписав в виде , получим уравнение с угловым коэффициентом , проходящей через заданную точку .

Задача 2. Через точку провести прямую, перпендикулярную вектору . Вектор , перпендикулярный прямой, называется нормальным вектором к прямой илинормалью к прямой.

Решение. Пусть точка — текущая точка искомой прямой. Тогда вектор перпендикулярен вектору . Тогда выписывая условие перпендикулярности, получим уравнение искомой прямой:

Раскрыв скобки и обозначив число , получим так называемое общее уравнение прямой:

В этом уравнении коэффициенты при и являются координатами нормального вектора прямой.

Всякая прямая разбивает плоскость на две полуплоскости, где с одной стороны прямой и с другой стороны. При этом точки той

части плоскости, куда смотрит вектор , удовлетворяет неравенству . Поэтому:

В направлении вектора функция возрастает, а в направлении вектора она убывает.

Пример 5. Написать уравнение прямой, проходящей через точку параллельно прямой .

Решение. У параллельных прямых нормальные вектора тоже параллельны, т.е. . Согласно задаче 2 получим искомое уравнение: или .

3. Системы двух линейных уравнений с параметрами

Решениями системы двух линейных уравнений являются точки пересечения двух прямых: и .

Возможны 3 случая:

1. Прямые не параллельны . Тогда и их нормальные вектора не параллельны, т.е. . В этом случае система имеет единственное решение.

2. Прямые параллельны и не совпадают. Тогда и их нормальные вектора параллельны, но сдвиги различны, т.е. .

В этом случае система решений не имеет .

3. Прямые совпадают. Тогда их нормальные вектора параллельны и сдвиги совпадают, т.е. . В этом случае система имеет бесконечно много решений – все точки прямой.

Пример 1. При всех значениях а и b решить систему уравнений

Решение. Выразим из первого уравнения и подставим во второе уравнение. Получим: .

Если — единственное решение. Если , то если , то решений бесконечно много: . Если

же , то решений нет.

Пример 2. При каком значении параметра а система уравнений

Решение. Система не имеет решений, если .

Пример 3. При всех значениях а решить систему уравнений

Решение. Система равносильна совокупности двух систем:

Прямые параллельны , если . При этом прямые не совпадают, поэтому при 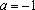решений нет.

Если 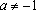, то выражая из второго уравнения и подставляя в первое, получим: .

Пример 4. Найти все такие значения а, что для любого значения b

найдётся хотя бы одно с такое, что система уравнений

имеет хотя бы одно решение.

Решение. Прямые не параллельны, если

В этом случае система имеет единственное решение при любом c.

По условию задачи система должна иметь решение при всех b.

Если то система принимает вид: . Чтобы при система также имела решения, нужно, чтобы уравнение относительно c имело хотя бы одно решение. Т.о., дискриминант этого уравнения должен быть неотрицательным, т.е.

Аналогично, если то система принимает вид: Чтобы при система также имела решения, нужно, чтобы уравнение

относительно c имело хотя бы одно решение. Т.о., дискриминант этого уравнения должен быть неотрицательным, т.е.

4. Системы двух линейных неравенств с параметрами

Пример 1. При каких значениях а система неравенств

не имеет решений?

Решение. Система имеет решения только если .

Ответ: при решением будет любой ;

при решений нет.

Пример 2. При каких значениях а система неравенств

имеет хотя бы одно решение?

Решение. При первое неравенство не имеет решений. А тогда и вся система не имеет решений.

Пусть , тогда и эта система не имеет решений, так как , а . Пусть , тогда т.е.

решения есть при , и , так как при выполнено неравенство , то решение запишется в виде .

Ответ: при решением будет любой ;

при решений нет.

Пример 3. При всех значениях а решить систему

Решение. Перепишем систему неравенств в виде . Рассмотрим все возможные случаи.

1) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем: при

2) . Тогда первое неравенство не верно. А значит, и вся система не имеет решений .

3) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем:

4) . Тогда второе неравенство не верно. А значит, и вся система не имеет решений .

5) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем: при

при и при решений нет.

Пример 4. При всех значениях а решить систему

При система не имеет решений.

Пусть , тогда и эта система не имеет решений.

Пусть , тогда и эта система будет иметь решения, если выполнено неравенство: .