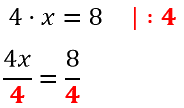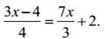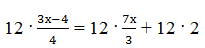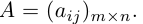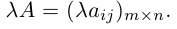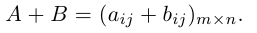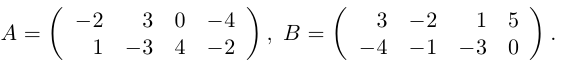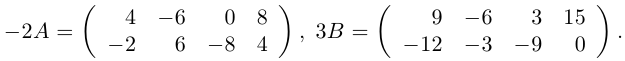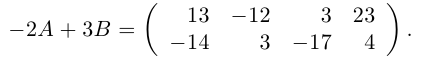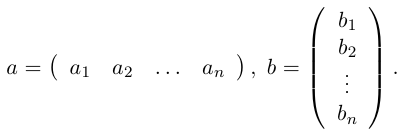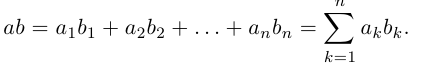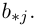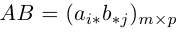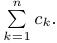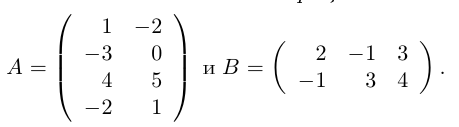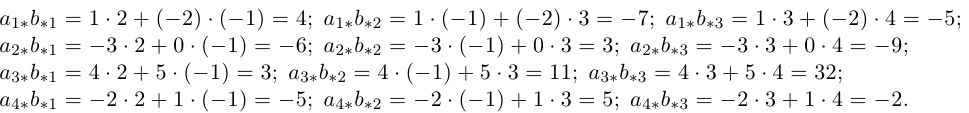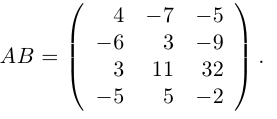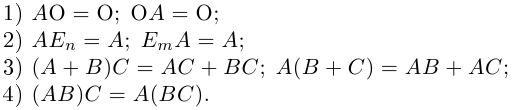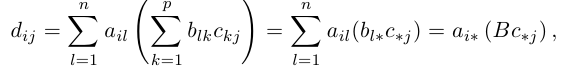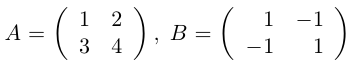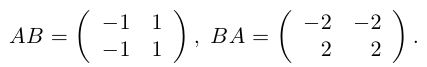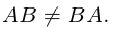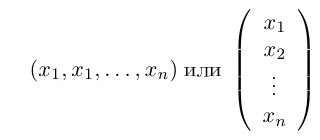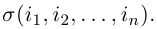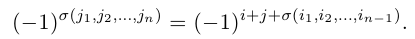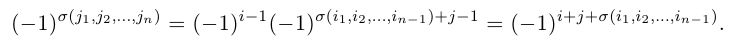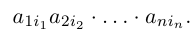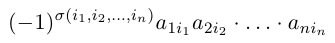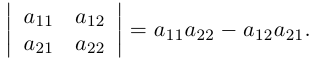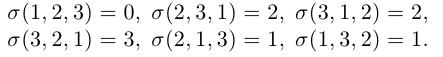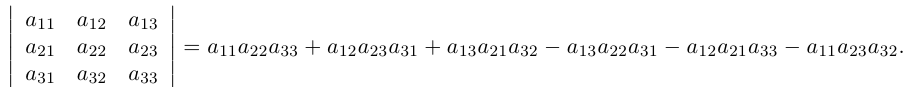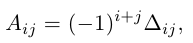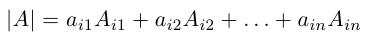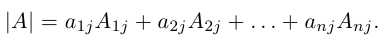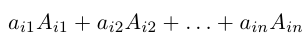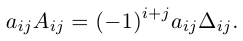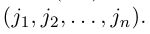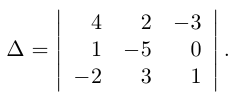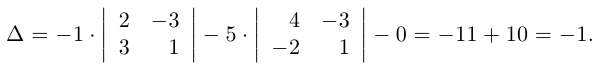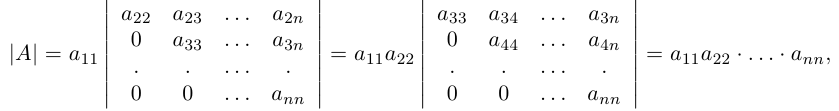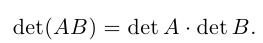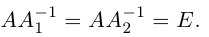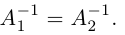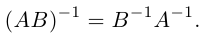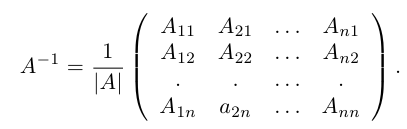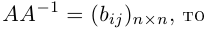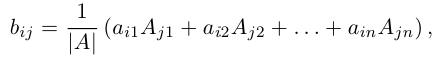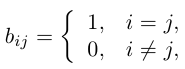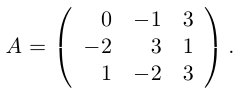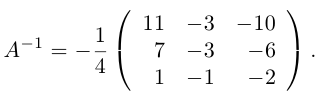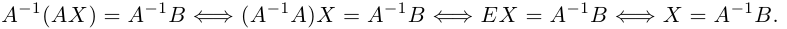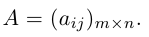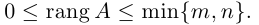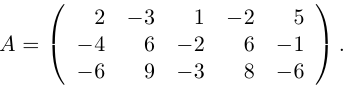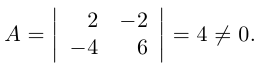Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Линейная алгебра — примеры с решением заданий и выполнением задач
Содержание:
Линейная алгебра
Линейная алгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения, системы линейных уравнений, среди основных инструментов, используемых в линейной алгебре — определители, матрицы, сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры.
Матрицы и операции над ними
В математике и ее приложениях наряду с числами часто бывает удобным использовать числовые таблицы, которые называются матрицами. Аппарат теории матриц эффективно применяется, например, при решении систем линейных уравнений, как мы скоро в этом убедимся. Перейдем к точным определениям.
Определение: Матрицей размерности m х n называется прямоугольная таблица действительных чисел, состоящая из m строк и n столбцов.
Числа, составляющие матрицу, называются ее элементами. Для доступа к элементам матрицы используются два индекса: первый указывает на номер строки, второй — на номер столбца, на пересечении которых расположен данный элемент.
Обозначаются матрицы, как правило, прописными латинскими буквами A, B, C,иногда указывается размерность, например, Amxn. В развернутой форме матрица записывается как таблица:
Более компактно с указанием элементов матрица записывается в виде:
Матрицы А и В одинаковой размерности считаются равными, если все элементы одной матрицы равны соответвующим элементам другой матрицы.
Рассмотрим некоторые специальные виды матриц.
Матрица, у которой все элементы равны нулю, называется нуль-матрицей и обозначается через O.
Матрица, у которой число строк равно числу столбцов, называется квадратной. Размерность квадратной матрицы часто называют ее порядком.
Числа 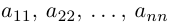
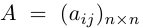
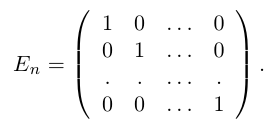
Квадратная матрица, диагональные элементы которой равны единице, а все остальные — нулю, называется единичной матрицей и обозначается через 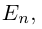
Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (выше) главной диагонали, равны нулю. Например, треугольной является матрица
Матрица называется трапециевидной, если она представляет собой следующую таблицу:
Операции над матрицами
Введем сначала линейные операции над матрицами.
Произведением действительного числа 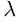
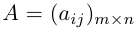
Суммой двух матриц 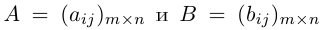
Таким образом, элементы суммы матриц равны суммам соответствующих элементов данных матриц.
Разность матриц А и B можно определить как А — В = А + (-1)В.
Свойства линейных операций над матрицами аналогичны соответствующим свойствам действительных чисел.
Пример №1
Найти матрицу -2А +3В.
Определим теперь операцию умножения матриц. Рассмотрим сначала матрицу-строку и матрицу-столбец с одинаковым числом элементов, т.е.
Произведением этих строки и столбца называется число1
Рассмотрим так называемые согласованные матрицы 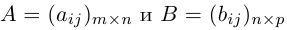
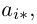
Произведением данных согласованных матриц А и B называется матрица
Часто для суммы n чисел 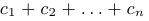
размерности m х p, элементы которой равны произведениям строк матрицы A на столбцы B.
Пример №2
Найти произведение согласованных матриц
Решение. Найдем произведение строк матрицы А на столбцы матрицы В.
Осталось записать искомое произведение матриц:
Отметим некоторые свойства произведения матриц1.
Первые три сразу следуют из определения произведения матриц. Докажем последнее свойство. Пусть заданы три матрицы 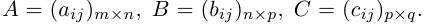
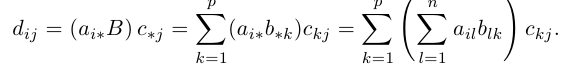
что представляет собой произведение Тем строки с номером i матрицы A на столбец с номером j матрицы ВС. Тем самым свойство 4 доказано.
Заметим, что в отличие от чисел матрицы, вообще говоря, не коммутируют (не перестановочны). Приведем соответствующий
Контрпример. Доказать, что матрицы
Таким образом, для этих матриц
Замечание. Пользуясь случаем, введем здесь определение n-мерного векторного пространства Rn, как множество упорядоченных совокупностей n действительных чисел. Каждую такую совокупность мы будем обозначать через и называть n-мерным вектором.
Мы предполагаем, что все матрицы в свойствах согласованы.
Очевидно, каждый вектор мы можем отождествить с соответствующей матрицей-строкой или матрицей-столбцом, поэтому на векторы автоматически переносятся линейные операции, которые мы определили выше для матриц.
Определитель матрицы и его свойства
Познакомимся теперь с такой важнейшей характеристикой матрицы, как определитель. Введем предварительно понятие перестановки и изучим некоторые ее свойства.
Перестановки
Перестановкой n натуральных чисел 1, 2, . n называется строка
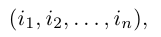
содержащая все эти числа.
Первым элементом перестановки может быть любое из чисел 1, 2, . n, вторым — любое из оставшихся n — 1 чисел и так далее, следовательно, число различных перестановок данных чисел равно 
Два числа в перестановке находятся в инверсии, если большее из них имеет меньший номер. Число всех инверсий в перестановке (1) мы обозначим через
В связи с этим перестановка (1) называется четной, если в ней число 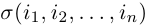
Отметим два свойства перестановок, которые мы будем использовать ниже.
Лемма 1. Характер четности перестановки изменится на противоположный, если в ней поменять местами какие-нибудь два элемента.
Доказательство. Предположим сначала, что меняются местами рядом стоящие элементы к и l перестановки. В этом случае число инверсий в новой перестановке изменится на единицу, а именно, увеличится на единицу, если к и l не находились в инверсии, или настолько же уменьшится, если они находились в инверсии. Таким образом, характер четности перестановки изменится на противоположный. Рассмотрим теперь случай, когда числа к и l разделяют s других элементов перестановки. Тогда поменять местами данные элементы мы можем последовательно переставляя число к с s промежуточными элементами, а затем переставляя число l в обратном порядке с элементом к и всеми s промежуточными. В результате мы выполним 2s + 1 обменов рядом стоящих элементов и, таким образом, характер четности исходной перестановки изменится нечетное число раз и, следовательно, он изменится на противоположный. Лемма доказана.
Из этой леммы сразу же следует, что количество четных перестановок равно количеству нечетных. В самом деле, поменяв местами любые два элемента в каждой из p четных перестановок, мы получим p нечетных и, следовательно, 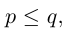
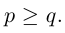
Лемма 2. Пусть
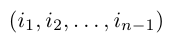
— перестановка чисел 1, 2, . n — 1. Зафиксируем число j из множества <1, 2, . , n>и оставим его перестановку (2) на место с номером i, сдвинув вправо на одну позицию все ее элементы с номерами i, i + 1, . , n — 1 и увеличив на единицу все не меньшие, чем j элементы этой перестановки. В результате получим перестановку
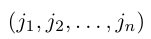
чисел 1, 2, . , n. Четности перестановок (2) и (3) связаны равенством
Действительно, предположим сначало, что элемент j в перестановке (3) стоит на первом месте. Тогда, очевидно, количество инверсий в этой перестановке равно 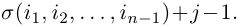
Определитель и его вычисление для матриц второго и третьего порядков
Рассмотрим квадратную матрицу порядка n :
Составим произведение элементов данной матрицы, взятых по одному из каждой строки и каждого столбца. Упорядочив элементы этого произведения по возрастанию номеров строк, мы можем записать его в виде:
Номера столбцов в записанном произведении образуют перестановку чисел 1, 2, . , n.
Определение: Число, равное сумме всех n! произведений
называется определителем данной квадратной матрицы А (определителем n-го порядка) и обозначается через |А| или det А. В развернутой форме определитель записывается как
Найдем пользуясь этим определением выражение для определителей второго и третьего порядков.
Так как 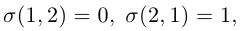
Аналогично, для вычисления определителя третьего порядка найдем число инверсий в каждой из перестановок чисел 1, 2, 3 :
Тогда
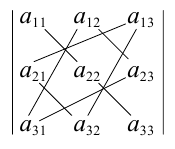
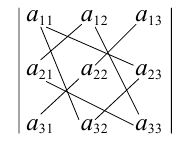
Для упрощения вычисления определителя третьего порядка можно использовать правило треугольников, согласно которому со знаком » + » следует брать произведения по схеме
а со знаком » — » — по схеме
Пример №3
Решение. Воспользуемся правилом треугольников: 
Свойства определителя
1) Если какая-либо строка (столбец) определителя состоит из нулей, то и определитель равен нулю.
2) Общий множитель элементов какой-либо строки (столбца) можно выносить за знак определителя.
3) Если все элементы какой-нибудь строки (столбца) определителя равны суммам двух слагаемых, то данный определитель равен сумме двух определителей, в которых в указанной строке (столбце) стоят, соответственно, первые и вторые слагаемые, а остальные элементы обоих определителей такие же, как и в исходном определителе.
Эти свойства напрямую следуют из определения определителя.
4) Если переставить две какие-нибудь строки (столбца) определителя, то он поменяет знак на противоположный.
Действительно, переставим, например, две строки определителя. В результате получим определитель, каждое слагаемое которого отличается знаком от соответствующего слагаемого исходного определителя, так как по доказанной в пункте 1 лемме 1 четность соответствующей перестановки вторых индексов изменится па противоположную.
5) Если в определителе совпадают (пропорциональны) две какие-нибудь строки (столбцы), то этот определитель равен нулю.
В самом деле, если в определителе совпадают две каие-нибудь строки (столбцы), то, с одной стороны, определитель при этом не изменится, а, с другой стороны, по предыдущему свойству его знак поменяется на противоположный. Таким образом |A| = — |A| и, стало быть, |A| = 0. Если же в определителе имеются две пропорциональные строки (столбца), то после вынесения за его знак по свойству 2) общего множителя элементов строки (столбца), мы получим определитель с двумя одинаковыми строками (столбцами), который равен нулю.
6) Определитель не изменится, если к элементам какой-нибудь строки (столбца) добавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.
Это следует из свойств 3) и 5), так как в этом случае полученный определитель можно представить в виде суммы двух определителей, один из которых равен исходному, а в другом имеются пропорциональные строки (столбцы), и поэтому он равен пулю.
Прежде чем сформулировать очередное свойство, введем понятие алгебраического дополнения к элементу матрицы.
Алгеброическим дополнением элемента aij квадратной матрицы A = (aij)nxn мы будем называть число
где 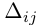
7) Разложение определителя по элементам строки (столбца).
Определитель матрицы равен сумме произведений элементов какой-нибудь строки (столбца) на соответствующие алгебраические дополнения. Таким образом,
Докажем, например, первую из этих формул. Убедимся в том, что правая часть данной формулы содержит все слагаемые определителя матрицы А. Выражение
содержит n(n — 1)! = n! различных произведений элементов определи теля матрицы A, взятых по одному из каждой строки и каждого столбца. Осталось проверить соответствие знаков.
Рассмотрим произвольное произведение
Каждое слагаемое определителя 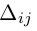
чисел 1, 2, . , n — 1. Умножив данное произведение на число 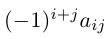
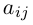
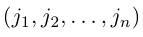
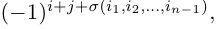
Таким образом, вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка.
Пример №4
Решение. Разложим этот определитель по элементам второй строки:
Пример №5
Вычислить определитель треугольной матрицы
Разлагая этот и следующие определители по первому столбцу, получим:
таким образом, определитель треугольной матрицы равен произведению диагональных элементов.
8) Сумма произведений n действительных чисел на алгебраические дополнения к элементам какой-нибудь строки (столбца) равна определителю, в котором в указанной строке (столбце) расположены данные числа, а все остальные элементы совпадают с соответствующими элементами исходного определителя.
Это свойство является прямым следствием предыдущего.
9) Сумма произведений элементов какой-нибудь строки (столбца) на алгебраические дополнения к элементам какой-нибудь другой строки (столбца) определителя равна нулю.
Действительно, по предыдущему свойству эта сумма произведений равна определителю с двумя совпадающими строками (столбцами), а такой определитель по свойству 5) равен нулю.
10) Определитель произведения матриц равен произведению определителей этих матриц, т. е.
Достаточно громоздкое доказательство этого свойства мы приводить не будем.
Обратная матрица
Определение: Обратной к квадратной матрице 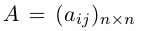
Из этого определения следует, что матрица А-1 также является квадратной той же размерности, что и матрица А.
Отметим некоторые свойства обратной матрицы, следующие из ее определения.
а) У матрицы не может существовать больше одной обратной.
Действительно, пусть для матрицы А имеются две обратные 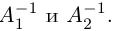
Умножив обе части первого равенства слева на матрицу 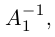
c) Если для квадратных матриц А и В одного порядка существуют обратные, то и у матрицы АВ также существует обратная , причем
Выясним условия, при которых обратная матрица существует.
Теорема (критерий существования обратной матрицы). Для того, чтобы существовала матрица, обратная данной, необходимо и достаточно, чтобы данная матрица была невырожденной, то есть чтобы ее определитель был не равен нулю.
Доказательство. Докажем сначала необходимость условия теоремы. Пусть для матрицы А существует обратная матрица. Тогда из равенства АА-1 = E, воспользовавшись свойством 10) определителя произведения матриц, получаем: det(AA-1) = det А 
Убедимся теперь в том, что условие теоремы является и достаточным. Предположим, что матрица А является невырожденной. Проверим, что обратной к данной является матрица со следующей структурой 1:
Действительно, если
откуда, воспользовавшись свойствами 7) и 9) определителя (§2, пункт 3), заключаем:
т. е. АА-1 = Е. Аналогично убеждаем, что А-1А = Е. Теорема доказана.
В строках указанной ниже матрицы записаны алгебраические дополнения к элементам соответствующих столбцов.
Пример №6
Найти обратную к матрице
Решение. Найдем сначала определитель матрицы: 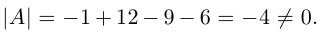
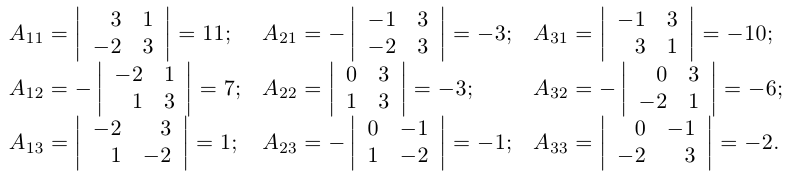
Обратную матрицу можно использовать при решении линейных матричных уравнений. Пусть, например, требуется решить матричное уравнение
с известными матрицами А и B, причем матрица A является невырожденной. Умножая обе части данного матричного уравнения слева на обратную матрицу A-1, получим:
Аналогично, решением матричного уравнения XA = B является матрица X = BA-1, а решением матричного уравнения AXB = С с невырожденными матрицами A и B является матрица X = A-1CB-1.
Ранг матрицы и его вычисление
Рассмотрим произвольную матрицу
Минором порядка k матрицы A называется определитель, стоящий на пересечении выбранных k строк и k столбцов данной матрицы.
Определение: Рангом матрицы А называется максимальный из порядков ненулевых миноров этой матрицы. Обозначается ранг через rang A.
Естественно считать, что rang O = 0. Очевидно также, что
Пример №7
Найти ранг матрицы
Решение. Вычислим минор, находящийся на пересечении первых двух строк и первого и четвертого столбцов:
Все же миноры третьего порядка этой матрицы равны нулю, так как третья строка равна разности второй и первой строк. Следовательно, rang A = 2.
Как видно из определения, вычисление ранга матрицы через миноры является весьма трудоемкой задачей, особенно для матриц большой размерности. Значительно сократить объем вычислений позволяет другой метод, основанный на элементарных преобразованиях матрицы.
Элементарными преобразованиями матрицы называются следующие операции над ее строками или столбцами:
- перестановка двух строк (столбцов) матрицы;
- умножение строки (столбца) на ненулевое действительное число;
- добавление к строке (столбцу) другой строки (столбца), умноженной на действительное число.
Тот факт, что матрица В получена из матрицы А с помощью одного или нескольких последовательно выполненных элементарных преобразований, мы будем обе тачать как
Теорема. Ранг матрицы не меняется при ее элементарных преобразованиях.
Доказательство этого утверждения для первого и второго элементарных преобразований следует из того, что по свойствам 2) и 4) определителя (§2, пункт 3) миноры исходной матрицы могут отличаться от миноров преобразованной разве лишь знаком или ненулевым множителем, что. естественно, не отражается на ранге матрицы. Пусть теперь матрица А’ получена из матрицы А с помощью третьего элементарного преобразования, для определенности будем считать, что к строке с номером i добавлена строка с номером j, умноженная на действительное число 
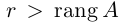
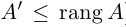
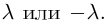
Следствие: Для того чтобы однородная система n уравнений с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы ее основной определитель был равен нулю.
Доказательство:
- Достаточность:
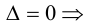 система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r
система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то rПри копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Линейная алгебра: пробный заезд
Аналит, линейка, линал — эти слова ассоциируются скорее с фразой «сдать и забыть», а не с тем, для чего на самом деле нужен замечательный раздел математики под названием линейная алгебра. Давайте попробуем посмотреть на него с разных сторон и разберемся, что же в нем хорошего и почему он так полезен в приложениях.
Часто первое знакомство с линейной алгеброй выглядит как-то так:
Не очень вдохновляет, правда? Сразу возникает два вопроса: откуда это все взялось и зачем оно нужно.
Начнем с практики
Когда я занимался вычислительной гидродинамикой (CFD), один из коллег говорил: «Мы не решаем уравнения Навье-Стокса. Мы обращаем матрицы.» И действительно, линейная алгебра — «рабочая лошадка» вычислительной математики:
Попробую проиллюстрировать эту связь на более простом примере, чем гидродинамика.
Пусть у нас есть тонкий металлический стержень с закрепленными концами, температура которых поддерживается равной нулю. Начнем греть стержень с помощью распределенного источника тепла, выделяющего q(x) Джоулей в секунду на единицу длины стержня в окрестности точки x. Какая температура t=t(x) установится? Сделаем очень грубый набросок модели. Когда установится равновесие, для каждого отрезка [x-h, x+h] нашего стержня приток тепла от источника должен быть равен сумме потоков тепла через границы отрезка. Если h достаточно мало, то с точностью до констант (в которые войдет h, да простят мне это читатели) это равенство можно записать так:
где Qx-h — поток тепла через левую границу, а Qx+h — через правую. Согласно закону Фурье тепловой поток пропорционален разности температур (ведь если нырнуть в бассейн, то в первые секунды будет холоднее всего). Поэтому (с точностью до констант, содержащих h)
Пусть h=1/N. Рассмотрим точки вида xi = i · h, где i=0, 1, 2, . N. Они называются сеткой. Тогда переменные ti=t(xi) будут удовлетворять уравнениям
где мы уже учли граничные условия, а qi=q(xi). Ну вот мы и получили систему линейных уравнений:
Конкретно эту систему можно решить «в лоб» так называемым методом прогонки, но в настоящих моделях системы становятся сложнее. Тут и приходит на помощь линейная алгебра, которая позволяет
- записать систему в короткой форме A · y = b (вот откуда взялось умножение матриц!);
- понять, имеет ли она решение и единственно ли оно;
- (в данном примере) найти его с помощью простой формулы y = A -1 b, как будто A — число;
- (перетекая в вычислительную математику) построить эффективные численные методы решения систем линейных уравнений.
И это — лишь взгляд на линейную алгебру с точки зрения математического моделирования. А еще есть квантовая механика, статистика и многое другое.
В качестве еще одного примера приведу известную задачу о ссылочном ранжировании страниц одного сайта (или интернета в целом).
Есть N страниц, каждая из которых может содержать ссылки на другие страницы. Требуется определить, какие страницы являются наиболее важными. Как именно измерять «важность» — часть задачи. Мы будем представлять ее количественно в виде неотрицательного числа (веса). Начнем с естественного предположения: чем больше ссылок на данную страницу, тем больше ее вес. В этом подходе есть следующий недостаток: мы не учитываем вес ссылающихся страниц. Логично, что ссылка со страницы, имеющий больший вес, должна иметь большее значение. Эти рассуждения приводят нас к такой модели:
где aij — количество ссылок на i-ую страницу с j-ой, разделенное на общее количество ссылок с j-й страницы. Эту формулу можно читать так: вес i-й страницы равен сумме произведений веса j-й страницы на долю ссылок с j-й страницы на i-ую. Таким образом, мы свели нашу задачу к системе линейных уравнений. Более того, вектор весов p оказывается собственным вектором матрицы A, отвечающим собственному значению 1:
Существование этого вектора (строго говоря, для немного модифицированной матрицы A) гарантируется теоремой Фробениуса-Перрона. А найти его можно методом простых итераций.
Итак, линейная алгебра — это очень универсальный набор идей и инструментов, которые можно применять в самых разных областях. Но бесплатен только сыр в мышеловке, и за универсальность приходится платить: некоторые определения и теоремы могут показаться излишне абстрактными и запутанными. Но это не так: на самом деле, многие абстракции призваны упрощать жизнь, а не усложнять ее. «Если это выглядит как утка, плавает как утка и крякает как утка, то, вероятно, это утка» — по сути абстракция, причем весьма удобная, если к ней привыкнуть. То же самое с линейной алгеброй. Чтобы проиллюстрировать этот момент немного конкретнее, давайте дополним наш «внешний осмотр» кратким обсуждением того, что внутри.
Теперь немного теории
Линейная алгебра изучает векторные пространства и функции, которые отображают одно векторное пространство в другое. В основном рассматриваются линейные функции (удовлетворяющие соотношению f(α · x + β · y) = α · f(x) + β · f(y) для любых чисел α и β и любых векторов x и y). Бывают и нелинейные (например, квадратичные формы). Но прежде всего нужно понимать что такое вектор (и векторное пространство). И это не так тривиально, как могло бы показаться.
В учебниках и курсах обычно приводится абстрактное определение из 8 пунктов. Еще иногда говорят, что векторное пространство — это аддитивно записанная абелева группа в которой определено умножение на скаляры, удовлетворяющее 4 аксиомам. Но тем, кто впервые изучает линейную алгебру, это вряд ли поможет разобраться. Гораздо проще рассмотреть несколько конкретных примеров, и увидеть в них аналогию. А определение из 8 пунктов — всего лишь формализация этой аналогии. Поэтому перейдем сразу к примерам.
Знакомые всем со школы направленные отрезки конечно же являются векторами. Множество направленных отрезков — пример векторного пространства. Теперь рассмотрим многочлены. Их можно складывать друг с другом и умножать на числа. Обратите внимание: с точки зрения алгебры эти операции сложения многочленов и умножения многочлена на число работают точно по тем же правилам, что и для направленных отрезков. Например, равенство x+y = y+x (коммутативность) выполняется как для направленных отрезков, так и для многочленов. Поэтому множество многочленов является векторным пространством, а многочлены — векторами.
Раз многочлены похожи на направленные отрезки, то у них тоже должны быть координаты. Но как их искать и сколько координат у многочлена? Всем хорошо известно что на плоскости каждый вектор имеет ровно две координаты, а в пространстве — три. Почему это так? И что такое размерность вообще? Линейная алгебра дает ответ на данный вопрос: размерность — это максимальное число линейно независимых векторов. Что значит линейно независимых? Векторы x1, x2, . xn называются линейно зависимыми если найдутся числа α1, α2, . αn, хотя бы одно из которых отлично от нуля, такие что
Если векторы не являются линейно зависимыми, то они называются линейно независимыми. (Понятие линейной зависимости обобщает понятия параллельных и компланарных векторов: два вектора линейно зависимы тогда и только тогда, когда они параллельны. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.)
Размерность пространства может быть как конечной (пространство многочленов степени не выше N), так и бесконечной (пространство всех многочленов). Оба случая встречаются на практике, но давайте ограничимся конечномерными. Пусть векторы x1, x2, . xn линейно независимы и n — размерность пространства. Тогда любой другой вектор x можно записать в виде линейной комбинации x1, x2, . xn, причем единственным образом. Коэффициенты соответствующей линейной комбинации и называются координатами.
Теперь у нас есть строгое определение координат. Но смысл не только в этом: по пути мы столкнулись с более фундаментальными (и менее заметными) понятиями линейной комбинации и линейной зависимости. А еще мы узнали что в n-мерном линейном пространстве не может быть больше, чем n линейно независимых векторов. Этот факт — один из краеугольных камней линейной алгебры.
Казалось бы, мы все еще знаем слишком мало, чтобы извлечь из этого хоть какую-то пользу. Однако уже сейчас мы можем решать задачи, на первый взгляд не имеющие отношения к линейной алгебре. Например, такую: даны многочлены p и q; существует ли многочлен от двух переменных R=R(x,y) такой, что R(p(t), q(t))=0 при всех t?
Тем временем наш «пробный заезд» подходит к концу. Но остается еще коротко обсудить различные способы изучения линейной алгебры. Ограничусь здесь небольшим обзором своего собственного опыта и попробую дать на основе него пару советов.
Википедия Книга — лучший источник знаний
Мое знакомство с линейной алгеброй началось с самостоятельного изучения книги О.В. Мантурова и Н.М. Матвеева «Курс высшей математики», когда я учился в школе. Эта книга — далеко не лучший (но и не худший) источник знаний в данной области. Просто она стала первым учебником по высшей математике, попавшим в мои руки, и ее содержание показалась мне более интересным, чем школьная программа. Хотя сейчас можно с уверенностью сказать: есть куча других книг, которые школьникам стоит (и будет не менее интересно) изучить в первую очередь. Например, «Как решают нестандартные задачи» (Канель-Белов А.Я., Ковальджи А.К.) или «Ленинградские математические кружки» (Генкин С.А., Итенберг И.В., Фомин Д.В.). Если же Вы возьметесь изучать линейную алгебру по книгам, то стоит запастись терпением: для достижения желаемого результата может потребоваться больше времени, чем кажется.
Своими основными знаниями линейной алгебры (и многих других разделов математики) я все же обязан Л.И. Коваленко — легендарному преподавателю МФТИ, семинары и консультации которой всегда собирали аншлаг. Сложно переоценить то внимание, которое она оказывала каждому студенту, до позднего вечера принимая задания и так называемые «карточки» — индивидуальные задачи. А еще во время этих сдач мы активно общались друг с другом. Все это позволяло не только быстрее освоить то, что написано в учебниках, но и то, чего там нет — интуицию, хитрые приемы и прочее.
Живое общение студентов с преподавателями (и друг с другом) ничто не заменит, и в этом преимущество традиционных курсов. Но когда я сам работал ассистентом и вел семинары, часто возникало желание некоторые вещи автоматизировать, чтобы на содержательное общение оставалось больше времени. Нужно ли студенту ждать встречи с преподавателем, чтобы получить стандартный ответ на стандартный вопрос? Или узнать правильно ли решена такая-то стандартная задача? Впрочем, не нужно недооценивать студентов: по большей части, они сами хорошо чувствуют когда делают «почти бессмысленную работу», и их это тоже демотивирует. Проверка доказательства или метода решения — это одно, но вот, скажем, проверку решения системы линейных уравнений можно практически полностью доверить компьютеру. Более того, во многих случаях можно автоматизировать не только проверку ответа, но и часть самого решения — например, элементарные преобразования матриц.
Итак,
- идеи и методы линейной алгебры проще всего понять решая интересные задачи (в том числе из других областей: это позволит лучше разобраться в абстрактных понятиях);
- лучше всего делать это не в одиночку, а вместе с друзьями и хорошим преподавателем (еще очень полезны различные форумы);
- если вас демотивируют рутинные действия — пользуйтесь онлайн-курсами и другими способами автоматизации (здесь нужно иметь чувство меры. Например, перед тем как обращать матрицы в Wolfram Alpha, стоит научиться это делать с помощью ручки и бумаги);
- книги позволяют двигаться вглубь, но не забывайте следить за временем;
- основные понятия и теоремы линейной алгебры не появились на пустом месте. Полезно стремиться понять мотивировки, внутреннюю логику и развивать свое интуитивное видение предмета. Ведь наверняка Крамеру, Гауссу, Пеано и многим другим было интересно открывать (прежде всего для себя) эти основы; почему же тем, кто изучает линейную алгебру сейчас, должно быть скучно это делать?
http://www.evkova.org/linejnaya-algebra
http://habr.com/ru/post/256275/