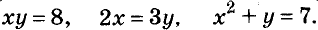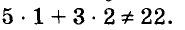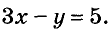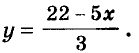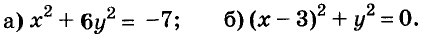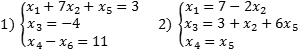Линейные дифференциальные уравнения в высшей математике
Содержание:
Линейные дифференциальные уравнения. Линейные дифференциальные уравнения первого порядка
В предыдущей лекции мы изучали дифференциальные уравнения с разделяющимися переменными. Другим часто встречающимся типом являются линейные дифференциальные уравнения.
Определение 1. Дифференциальное уравнение вида

называется линейным дифференциальным уравнением первого порядка. Если 

где 

называется линейным однородным уравнением, соответствующим уравнению (2).
Уравнение (2) — это уравнение с разделяющимися переменными. Действительно

Интегрируя это уравнение, получим
где 



где 
Одним из наиболее удобных методов решения уравнения (2) является метод подстановки 
Применим этот метод к уравнению (2). Получим
Приравняем выражение в квадратных скобках к нулю и найдем одно из решений этого дифференциального уравнения. Тогда линейное дифференциальное уравнение (2) будет сведено к системе двух дифференциальных уравнений с разделяющимися переменными
Найдя из системы (4) функции 


Пример №122

Решение:
Данное уравнение — это ЛДФУ первого порядка (2). Применим метод подстановки 
Составим систему (4):
Решим первое уравнение системы:
Так как нам нужно одно ЧР ДФУ, то возьмем 
Решаем второе уравнение:
Итак, OP Л ДФУ будет таким:

Убедимся проверкой в правильности решения:
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Рассмотрим линейное дифференциальное уравнение (ЛДФУ) второго порядка с постоянными коэффициентами

где 
Уравнению (5) соответствует однородное ЛДФУ:

Пусть 


Теорема 1. Общее решение неоднородного уравнения (5) есть сумма общего решения соответствующего ему однородного уравнения (6) и частного решения неоднородного уравнения (5):

Рассмотрим однородное ЛДФУ (6). Имеет место следующий результат.
Теорема 2. Пусть 


Ранее мы отмечали, что ОР ДФУ 2-го порядка зависит от двух произвольных констант. Из теоремы 2 следует, что функция

является решением уравнения (6). Возникает вопрос: может ли формула (8) определять ОР ДФУ (6). Если да, то при каких условиях? Чтобы разобраться в этом, введем несколько понятий, аналогичных сведениям из линейной алгебры.
Определение 2. Функции 

только лишь в случае 
Определение 3. Систему функций 
Имеет место следующий факт.
Теорема 3. Пусть 

Фундаментальный набор решений уравнения (6) находят методом Эйлера в виде функций 





Так как 

Определение 4. Алгебраическое уравнение (10) называется характеристическим уравнением однородного ЛДФУ (6).
При решении характеристического уравнения могут возникать три случая.
Случай 1. Дискриминант 





Пример №123

Решение:
Корнями характеристического уравнения
являются числа 


Проверкой можно убедиться в правильности решения.
Случай 2. Дискриминант 



Таким образом, ОР имеет вид

Пример №124

Решение:
имеет единственный действительный корень 

Проверкой можно убедиться в правильности решения.
Случай 3. Дискриминант
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
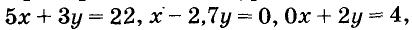
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 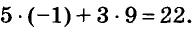
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 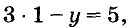
Уравнение 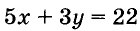
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 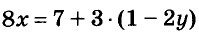
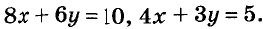
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 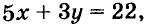
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения 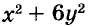
б) Значение выражения 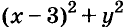
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 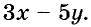
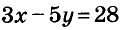
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 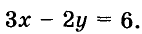
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Системы линейных уравнений: основные понятия
— это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.
— это последовательность чисел ( k 1, k 2, . kn ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x 1, x 2, . xn дает верное числовое равенство.
Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
- Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
- Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
- Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.
Переменная xi называется , если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной xi должен быть равен нулю.
Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:
Обе системы являются разрешенными относительно переменных x 1, x 3 и x 4. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x 1, x 3 и x 5. Достаточно переписать самое последнее уравнение в виде x 5 = x 4.
Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:
- Число разрешенных переменных r равно общему числу переменных k : r = k . Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x 1 = b 1, x 2 = b 2, . xk = bk ;
- Число разрешенных переменных r меньше общего числа переменных k : r k . Остальные ( k − r ) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Так, в приведенных выше системах переменные x 2, x 5, x 6 (для первой системы) и x 2, x 5 (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:
Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.
Теорема. Если в системе из n уравнений переменные x 1, x 2, . xr — разрешенные, а x r + 1, x r + 2, . x k — свободные, то:
- Если задать значения свободным переменным ( x r + 1 = t r + 1, x r + 2 = t r + 2, . xk = tk ), а затем найти значения x 1, x 2, . xr , получим одно из решений.
- Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.
В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.
Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.
И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.
http://www.evkova.org/sistemyi-linejnyih-uravnenij
http://www.berdov.com/works/algebra/system_of_linear_equations/