Линейно зависимые и линейно независимые функции. Примеры исследования функций на линейную зависимость по определению.
Функции $y_1(x),\;y_2(x),\;y_3(x),\ldots,y_n(x)$ называются линейно зависимыми на некотором множестве $T$, если существуют такие константы $\alpha_1,\;\alpha_2,\;\alpha_3,\ldots,\alpha_n$, что $\forall x\in T$ выполняется следующее равенство:
$$ \begin
Примечание к терминологии: показать\скрыть
В определении использован термин «равенство», хотя можно было бы воспользоваться термином «тождество». Фразы «для каждого значения переменной $x\in T$ выполняется равенство $a(x)=b(x)$» и «на множестве $T$ верно тождество $a(x)\equiv b(x)$» равносильны. Например, фраза «равенство $\sin^2x=1-\cos^2x$ выполнено для $\forall x\in R$», равносильна такой: «на множестве $R$ верно тождество $\sin^2x=1-\cos^2x$». Т.е. вместо слов о том, что «$\forall x\in T$ выполняется следующее равенство: $\alpha_1\cdot y_1+\alpha_2\cdot y_2+\ldots+\alpha_n\cdot y_n=0$» можно сказать так: «на множестве $T$ верно тождество $\alpha_1\cdot y_1+\alpha_2\cdot y_2+\ldots+\alpha_n\cdot y_n\equiv 0$». Некоторые авторы предпочитают использовать именно термин «тождество».
Условие (2) можно изложить и в такой формулировке: среди коэффициентов $\alpha_i$ есть хотя бы один, не равный нулю.
Несложно убедиться в равносильности формулировок. Равенство $\alpha_<1>^<2>+\alpha_<2>^<2>+\ldots+\alpha_
Если же равенство (1) возможно лишь при условии:
то функции $y_1(x),\;y_2(x),\;y_3(x),\ldots,y_n(x)$ именуют линейно независимыми на множестве $T$. По сути, условие (3) равносильно такому: все коэффициенты $\alpha_i$ равны нулю.
Для двух функций несложно вывести простое правило: если $\forall x\in T$ $\frac
Обоснование этого правила: показать\скрыть
Допустим, что $\frac
Если же $\frac
Все примеры, указанные в этой теме, будут опираться на определения и свойство, приведенные выше. Естественно, что в общем случае применение таких определений несколько затруднительно. Существует несколько критериев, которые позволяют упростить процесс проверки функций на линейную зависимость. На сайте рассмотрены два таких способа: с помощью определителя Вронского и определителя Грама.
Выяснить, являются ли функции $y_1(x)=x^2+2x-4$, $y_2(x)=-4x^2+7x-1$, $y_3(x)=-5x^2+20x-14$ линейно зависимыми или линейно независимыми на множестве $R$.
Рассмотрим линейную комбинацию этих функций: $\alpha_1\cdot y_1+\alpha_2\cdot y_2+\alpha_3\cdot y_3$. Если $\forall x\in R$ равенство $\alpha_1\cdot y_1+\alpha_2\cdot y_2+\alpha_3\cdot y_3=0$ выполняется только при $\alpha_1=\alpha_2=\alpha_3=0$, то рассматриваемые функции линейно независимы. Если же $\forall x\in R$ равенство $\alpha_1\cdot y_1+\alpha_2\cdot y_2+\alpha_3\cdot y_3=0$ возможно при условии, что хотя бы один из коэффициентов $\alpha_i$ не равен нулю, то функции линейно зависимы.
Подставим в выражение $\alpha_1\cdot y_1+\alpha_2\cdot y_2+\alpha_3\cdot y_3=0$ заданные функции:
Раскроем скобки и перегруппируем слагаемые:
$$ \alpha_1\cdot x^2+2\alpha_1\cdot x-4\alpha_1-4\alpha_2\cdot x^2+7\alpha_2\cdot x-\alpha_2-5\alpha_3\cdot x^2+20\alpha_3\cdot x-14\alpha_3=0; $$ $$(\alpha_1-4\alpha_2-5\alpha_3)\cdot x^2+(2\alpha_1+7\alpha_2+20\alpha_3)\cdot x+(-4\alpha_1-\alpha_2-14\alpha_3)=0.$$
Последнее равенство возможно лишь в том случае, когда коэффициенты при степенях переменной $x$ одновременно равны нулю, т.е.:
Мы получили однородную систему линейных уравнений. Нам нет необходимости в её решении, нужно лишь установить количество решений. Если решение лишь одно – нулевое (или, в иной терминологии, тривиальное), т.е. $\alpha_1=\alpha_2=\alpha_3=0$, то функции линейно независимы. Если же есть иные решения, кроме нулевого, то функции линейно зависимы. Найдем ранг матрицы системы $A= \left( \begin
Отсюда получаем решение: $\left\< \begin
$$ 3\cdot y_1+2\cdot y_2-y_3=3\cdot(x^2+2x-4)+2\cdot(-4x^2+7x-1)-(-5x^2+20x-14)=0. $$
Итак, существуют такие константы $\alpha_1;\;\alpha_2;\;\alpha_3$ (например, $\alpha_1=3;\;\alpha_2=2;\;\alpha_3=-1$), не все одновременно равные нулю, что на $R$ выполняется тождество $\alpha_1\cdot y_1+\alpha_2\cdot y_2+\alpha_3\cdot y_3\equiv 0$. Следовательно, рассматриваемые функции линейно зависимы.
Исследовать на линейную зависимость такие функции: $y_1(x)=x\ln(x+4);\;y_2(x)=\ln^2(x+4)$.
Исследование проведем в интервале $T=(-4;+\infty)$, который представляет собой область определения заданных функций. Применим правило для определения линейной зависимости двух функций, указанное в начале страницы. Так как при $x\in(-4;+\infty)$ имеем: $\frac
Исследовать на линейную зависимость функции: $y_1(x)=1$, $y_2(x)=x$, $y_3(x)=x^2$, $y_4(x)=x^3$, $y_5(x)=x^4$.
Область определения этих функций есть вся числовая прямая, т.е. $x \in R$. Рассмотрим равенство:
$$ \begin
Если равенство (4) для всех $x\in R$ возможно лишь при условии $\alpha_1=\alpha_2=\alpha_3=\alpha_4=\alpha_5=0$, то заданные функции линейно независимы. Если же равенство (4) $\forall x\in R$ выполняется на наборе констант $\alpha_1$, $\alpha_2$, $\alpha_3$, $\alpha_4$, $\alpha_5$, среди которых хотя бы одна отлична от нуля, то заданные функции линейно зависимы. Итак, нужно исследовать равенство (4).
В левой части равенства (4) расположен многочлен, порядок (или, в иной терминологии, степень) которого не превышает $4$. Например, если $\alpha_1=2; \;\alpha_2=0;\;\alpha_3=0;\;\alpha_4=7;\;\alpha_5=0$, то получим многочлен третьего порядка:
$$\alpha_1\cdot 1+\alpha_2\cdot x+\alpha_3\cdot x^2+\alpha_4\cdot x^3+\alpha_5\cdot x^4=7x^3+2.$$
Т.е. в левой части равенства (4) может быть многочлен четвертого, третьего, второго, первого и нулевого порядков.
Рассмотрим случай, когда в левой части равенства (4) расположен многочлен, порядок которого не равен нулю (среди констант $\alpha_2;\;\alpha_3;\;\alpha_4;\;\alpha_5$ хотя бы одна не равна нулю). Любой многочлен первого порядка может обратиться в ноль только в одной точке (т.е. существует только одно значение $x$, при котором многочлен первого порядка равен нулю). Многочлен второго порядка равен нулю не более, чем в двух точках; многочлен третьего порядка – не более, чем в трёх точках; многочлен четвертого порядка обращается в ноль не более, чем в четырёх точках. Т.е. если среди констант $\alpha_2;\;\alpha_3;\;\alpha_4;\;\alpha_5$ есть хотя бы одна, отличная от нуля, то равенство (4) может быть выполнено не более, чем при четырёх значениях $x$ (а не для всех $x\in R$).
Рассмотрим ситуацию, когда среди констант $\alpha_2;\;\alpha_3;\;\alpha_4;\;\alpha_5$ нет ни одной, отличной от нуля, т.е. $\alpha_2=\alpha_3=\alpha_4=\alpha_5=0$. В этом случае в левой части равенства (4) получим многочлен нулевого порядка:
$$\alpha_1\cdot 1+\alpha_2\cdot x+\alpha_3\cdot x^2+\alpha_4\cdot x^3+\alpha_5\cdot x^4=\alpha_1$$
А само равенство (4) станет таким: $\alpha_1=0$. Следовательно, для многочлена нулевого порядка выполнение равенства (4) возможно лишь при $\alpha_1=\alpha_2=\alpha_3=\alpha_4=\alpha_5=0$.
Подведём итоги: если в правой части равенства (4) стоит многочлен ненулевого порядка, то равенство (4) не может быть выполнено при всех $x\in R$. Равенство (4) может быть выполнено для всех $x\in R$ только когда в правой части стоит многочлен нулевого порядка, однако это означает $\alpha_1=\alpha_2=\alpha_3=\alpha_4=\alpha_5=0$. Так как равенство (4) выполняется для всех $x\in R$ только при условии $\alpha_1=\alpha_2=\alpha_3=\alpha_4=\alpha_5=0$, то заданные функции линейно независимы на $R$.
Исследовать на линейную зависимость функции: $y_1(x)=4$, $y_2(x)=\arcsin
Так как $\arcsin x+\arccos x=\frac<\pi> <2>\; \forall x \in [-1;1]$ то:
$$\arcsin x+\arccos x=\frac<\pi><8>\cdot4; \; \arcsin x+\arccos x-\frac<\pi><8>\cdot4=0; \; 1\cdot y_1+1\cdot y_2+\left(-\frac<\pi><8>\right)\cdot y_3=0$$
Итак, существует такой набор констант $\alpha_1; \; \alpha_2;\; \alpha_3$ (например, $\alpha_1=1;\; \alpha_2=1;\; \alpha_3=-\frac<\pi><8>$), среди которых есть хотя бы одна константа, отличная от нуля, что равенство $\alpha_1\cdot y_1+\alpha_2\cdot y_2+\alpha_3\cdot y_3=0$ будет выполнено для всех $x\in[-1;1]$. Это означает, что функции $y_1(x)=4$, $y_2(x)=\arcsin
Исследовать на линейную зависимость функции: $y_1(x)=x;\; y_2(x)=|x|$ в их области определения.
Областью определения заданных функций есть все множество действительных чисел, т.е. $x\in R$. Функции будут линейно зависимыми, если существует такой набор констант $\alpha_1$ и $\alpha_2$, что для всех значений $x\in R$ выполнено равенство $\alpha_1\cdot y_1+\alpha_2\cdot y_2=0$ (т.е. $\alpha_1\cdot x+\alpha_2\cdot |x|=0$), причем хотя бы один из коэффициентов ($\alpha_1$ или $\alpha_2$) не равен нулю. Если же выполнение равенства $\alpha_1\cdot y_1+\alpha_2\cdot y_2=0$ при $\forall x\in R$ возможно лишь при $\alpha_1=\alpha_2=0$, то заданные функции будут линейно независимыми. Рассмотрим равенство $\alpha_1\cdot x+\alpha_2\cdot |x|=0$ подробнее.
Если $x≥ 0$, то $|x|=x$, поэтому равенство $\alpha_1\cdot x+\alpha_2\cdot |x|=0$ станет таким: $\alpha_1\cdot x+\alpha_2\cdot x=0$, $x\cdot(\alpha_1+\alpha_2)=0$. Равенство $x\cdot(\alpha_1+\alpha_2)=0$ должно быть выполнено при всех $x≥ 0$, поэтому $\alpha_1+\alpha_2=0$.
Итак, чтобы равенство $\alpha_1\cdot x+\alpha_2\cdot |x|=0$ было верным для всех $x\in R$, требуется выполнение двух условий:
Полученная система имеет лишь тривиальное (нулевое) решение: $\alpha_1=\alpha_2=0$. Итак, выполнение равенства $\alpha_1\cdot x+\alpha_2\cdot |x|=0$ при $\forall x\in R$ возможно лишь в случае $\alpha_1=\alpha_2=0$, поэтому функции линейно независимы на R.
Исследование на линейную зависимость с помощью определителей Вронского и Грама указаны в дальнейших темах сайта.
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
График линейной функции, его свойства и формулы
О чем эта статья:
Понятие функции
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 0 | 2 | 4 |
| y | -2 | -1 | 0 |
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
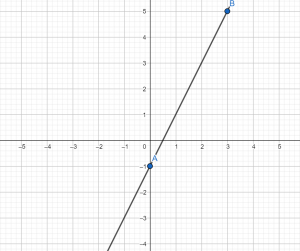
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Если k > 0 и b
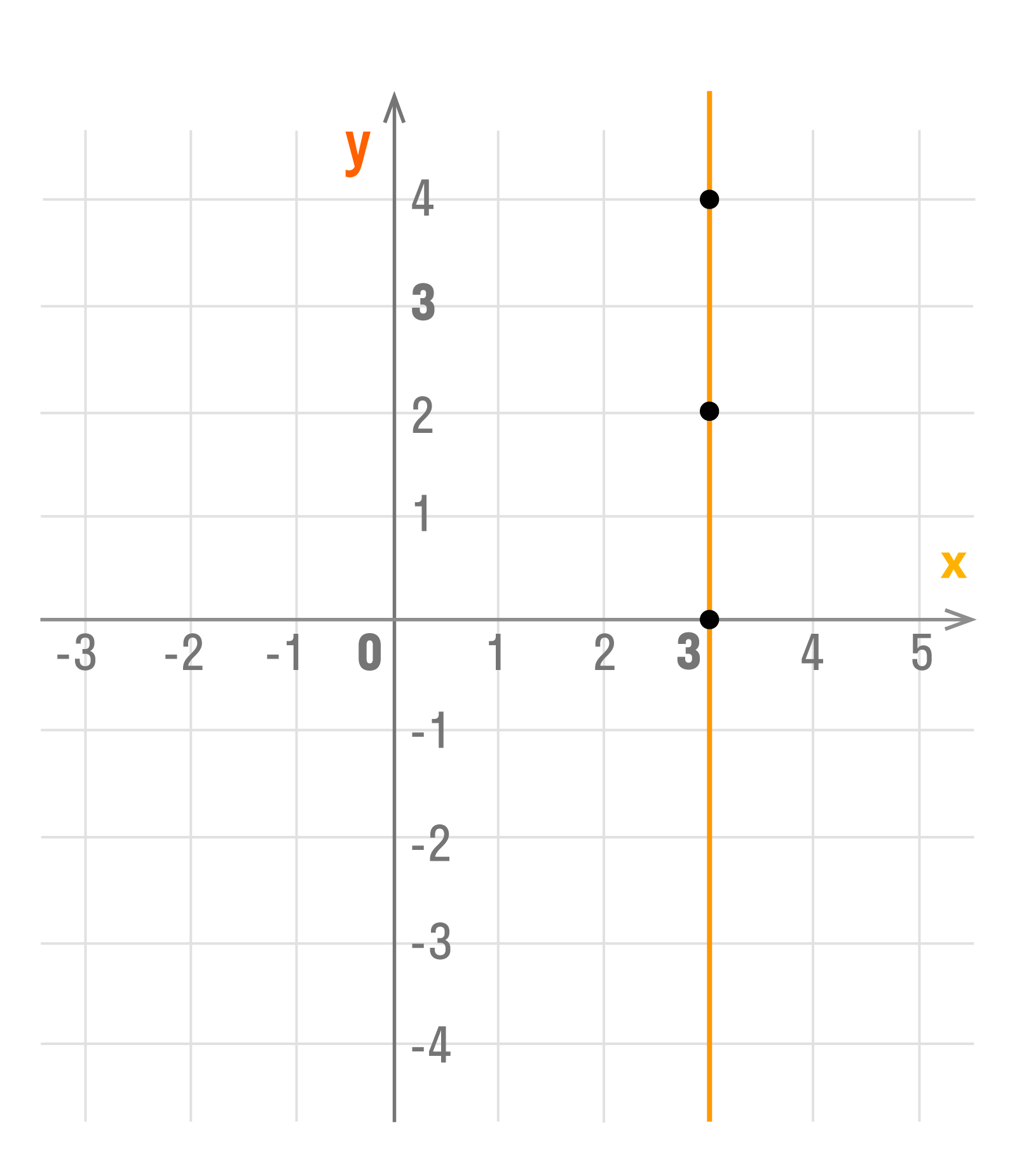
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
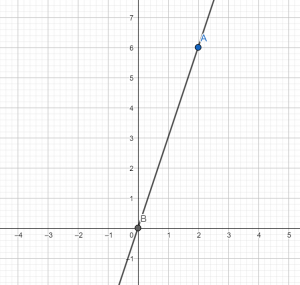
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
Линейная функция, ее свойства и график
теория по математике 📈 функции
Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
Свойства линейной функции
- Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
- Областью значений также является множество всех действительных чисел.
- Функция не имеет ни наибольших, ни наименьших значений.
- При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
- При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
- При k=0 прямая параллельна оси х.
- Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
| х |
| у |
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
| х | 0 | 3 |
| у |
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
у=2х – 1=2 × 0 – 1= –1;
у=2х – 1=2 × 3 – 1= 5.
Вписываем в таблицу значения у:
| х | 0 | 3 |
| у | –1 | 5 |
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5),
Проводимость — способность живой ткани проводить возбуждение.
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
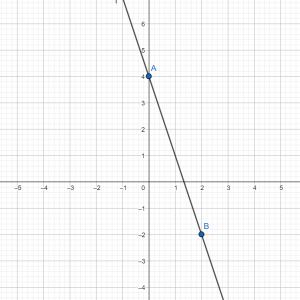
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
| х | 0 | 2 |
| у | 4 | –2 |
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
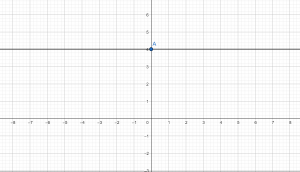
Пример №3
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ассмотрим коэффициенты под №3. Если k 90 0 ) угол с положит.направлением оси абсцисс (Ох). Если b 0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом ( 0 ). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b 0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
График данной функции зависит от k и b.
- если k 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k
pазбирался: Даниил Романович | обсудить разбор | оценить
http://skysmart.ru/articles/mathematic/grafik-linejnoj-funkcii
http://spadilo.ru/linejnaya-funkciya-ee-svojstva-i-grafik/