Линия задана уравнением в декартовой

Лекция Линии на плоскости и их уравнения

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Лекция № 7. Тема 1 : Линии на плоскости и их уравнения

1.1. Линии и их уравнения в декартовой системе координат

В аналитической геометрии линии на плоскости рассматриваются как геометрическое место точек (г. м.т.), обладающих одинаковым свойством, общим для всех точек линии.

О пределение. Уравнение линии – это уравнение с двумя переменными х и у , которому удовлетворяют координаты любой точки линии и не удовлетворяют координаты никакой другой точки, не лежащей на данной линии.

Верно и обратное, т.е. любое уравнение у

вида , вообще говоря, в декартовой

системе координат (ДСК) определяет линию

как г.м.т., координаты которых удовлетворяют

этому уравнению. О х

Замечание 1. Не всякое уравнение вида определяет линию. Например, для уравнения не существует точек, координаты, которых удовлетворяли бы этому уравнению. Такие случаи в дальнейшем рассматривать не будем. Это случай так называемых мнимых линий.

П ример 1. Составить уравнение окружности радиуса R с центром в точке .

Для любой точки , лежащей у М

на окружности, в силу определения R

окружности как г.м.т., равноудаленных

от точки , получаем уравнение х

1.2. Параметрические уравнения линий

Существует ещё один способ задавать линию на плоскости при помощи уравнений, которые называются параметрическими :

Пример 1. Линия задана параметрическими уравнениями

Требуется получить уравнение этой линии в ДСК.

Исключим параметр t . Для этого возведём обе части этих уравнений в квадрат и сложим

Пример 2. Линия задана параметрическими уравнениями

Требуется получить уравнение

этой линии в ДСК. — а а

Поступим аналогично, тогда получим

— а

Замечание 2. Следует отметить, что параметром t в механике явля-ется время.

1.3. Уравнение линии в полярной системе координат

ДСК является не единственным способом определять положение точки и, следовательно, задавать уравнение линии. На плоскости часто целесо-образно использовать так называемую полярную систему координат (ПСК).

П СК будет определена, если задать точку О – полюс и луч ОР , исхо-дящий из этой точки, который называется полярной осью. Тогда положение любой точки определяется двумя числами: полярным радиусом и полярным углом – угол между

полярной осью и полярным радиусом.

Положительное направление отсчета

полярного угла от полярной оси

считается против часовой стрелки.

Для всех точек плоскости , О Р

а для однозначности полярного угла считается .

Если начало ДСК совместить с

полюсом, а ось Ох направить по

полярной оси, то легко убедиться у

в связи между полярными и

декартовыми координатами:

О х Р

(1)

Если уравнение линии в ДСК имеет вид , то в ПСК — Тогда из этого уравнения можно получить урав-нение в виде

Пример 3. Составить уравнение окружности в ПСК, если центр окружности находится в полюсе.

Используя формулы перехода (1) от ДСК к ПСК, получим

Пример 4. Составить уравнение окружности,

если полюс на окружности, а полярная ось у

проходит через диаметр.

Поступим аналогично

О 2 R х

Данное уравнение можно получить и

из геометрических представлений (см. рис.).

П ример 5. Построить график линии

Перейдём к ПСК. Уравнение

примет вид О

График линии построим с а

учётом его симметрии и ОДЗ

функции:

Данная линия называется лемнискатой Бернулли .

1.4. Преобразование системы координат.

Уравнение линии в новой системе координат

1. Параллельный перенос ДСК. у

Рассмотрим две ДСК, имеющие М

одинаковое направление осей, но

различные начала координат.

В системе координат Оху точка

относительно системы О х

имеет координаты . Тогда имеем

В координатной форме полученное векторное равенство имеет вид

или . (2)

Формулы (2) представляют собой формулы перехода от «старой» системы координат Оху к «новой» системе координат и наоборот.

Пример 5. Получить уравнение окружности выполнив параллельный перенос системы координат в центр окружности.

И з формул (2) следует у

2. Поворот системы координат. М

Рассмотрим две системы координат

с общим началом, но с различными

направлениями осей. В системе коор-

динат Оху вектор , О х

а в системе координат вектор

Разложим векторы по базису :

Тогда имеем ,

откуда, переходя к координатной форме, получим формулы перехода

(3) (4)

Формулы (3) представляют собой переход от «старой» системы координат Оху к «новой» системе , а формулы (4) – наоборот.

Пример 6. Составить уравнение гиперболы при повороте системы координат на угол .

Используя формулы (3), получаем

или (каноническое уравнение гиперболы).

3. Общий случай: поворот вместе с параллельным переносом осущест-вляется согласно формулам (2) и (3):

(5)

Для того, чтобы получить уравнение линии в новой системе координат, необходимо в это уравнение подставить формулы (5).

Уравнение прямой, виды уравнения прямой на плоскости

В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.

Определение уравнения прямой на плоскости

Допустим, что есть прямая линия, которая задана в прямоугольной декартовой системе координат O х у .

Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе O x y , называется уравнением прямой на плоскости.

Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y . Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии.

Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.

Общее уравнение прямой линии

Познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости в декартовой системе координат O x y .

Уравнение вида A x + B y + C = 0 , где x и y – переменные, а А , В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат O x y . В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида A x + B y + C = 0 .

Таким образом, общее уравнение прямой на плоскости имеет вид A x + B y + C = 0 .

Поясним некоторые важные аспекты темы.

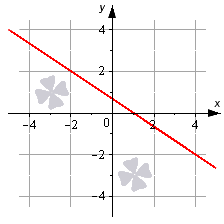
Посмотрите на рисунок.

Линия на чертеже определяется уравнением вида 2 x + 3 y — 2 = 0 , так как координаты любой точки, составляющей эту прямую, удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2 x + 3 y — 2 = 0 , дают нам прямую линию, которую мы видим на рисунке.

Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А , В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида A x + B y = 0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение A x + B y + C = 0 задает прямую, расположенную параллельно оси абсцисс O x . Если B равно нулю, то линия параллельна оси ординат O y .

Вывод: при некотором наборе значений чисел А , В и C с помощью общего уравнения прямой можно записать любую прямую линию на плоскости в прямоугольной системе координат O х у .

Прямая, заданная уравнением вида A x + B y + C = 0 , имеет нормальный вектор прямой с координатами A , B .

Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.

Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.

Уравнение прямой в отрезках

Уравнение прямой в отрезках имеет вид x a + y b = 1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.

Благодаря уравнению можно легко построить прямую линию на чертеже. Для этого необходимо отметить в прямоугольной системе координат точки a , 0 и 0 , b , а затем соединить их прямой линией.

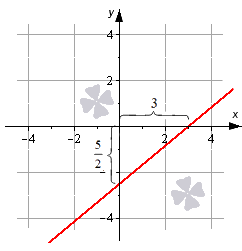
Построим прямую, которая задана формулой x 3 + y — 5 2 = 1 . Отмечаем на графике две точки 3 , 0 , 0 , — 5 2 , соединяем их между собой.

Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».

Уравнение прямой с угловым коэффициентом

Эти уравнения, имеющие вид y = k · x + b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x .

Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси O x .

Для обозначения угла наклона прямой к положительному направлению оси O x в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси O x или совпадает с ней.

Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывается это следующим образом k = t g α . Для прямой, которая располагается параллельно оси O y или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).

Прямая, которая задана уравнением y = k · x + b , проходит через точку 0 , b на оси ординат. Это значит, что уравнение прямой с угловым коэффициентом y = k · x + b , задает на плоскости прямую линию, которая проходит через точку 0 , b и образует угол α с положительным направлением оси O x , причем k = t g α .

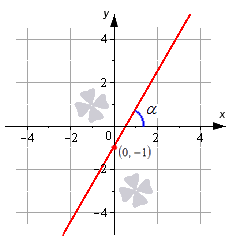
Изобразим прямую линию, которая определяется уравнением вида y = 3 · x — 1 .

Эта линия должна пройти через точку ( 0 , — 1 ) . Угол наклона α = a r c t g 3 = π 3 равен 60 градусов к положительному направлению оси O x . Угловой коэффициент равен 3

Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.

Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.

Каноническое уравнение прямой на плоскости

Данный вид уравнения имеет вид x — x 1 a x = y — y 1 a y , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не равны нулю.

Прямая линия, заданная каноническим уравнением прямой, проходит через точку M 1 ( x 1 , y 1 ) . Числа a x и a y в знаменателях дробей представляют собой координаты направляющего вектора прямой линии. Это значит, что каноническое уравнение прямой линии x — x 1 a x = y — y 1 a y в декартовой системе координат O x y соответствует линии, проходящей через точку M 1 ( x 1 , y 1 ) и имеющей направляющий вектор a → = ( a x , a y ) .

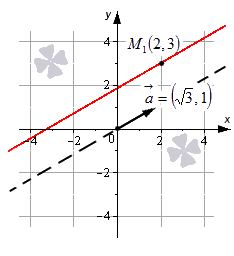
Изобразим в системе координат O x y прямую линию, которая задается уравнением x — 2 3 = y — 3 1 . Точка M 1 ( 2 , 3 ) принадлежит прямой, вектор a → ( 3 , 1 ) является направляющим вектором этой прямой линии.

Каноническое уравнение прямой линии вида x — x 1 a x = y — y 1 a y может быть использовано в случаях, когда a x или a y равно нулю. Наличие ноля в знаменателе делает запись x — x 1 a x = y — y 1 a y условной. Уравнение можно записать следующим образом a y ( x — x 1 ) = a x ( y — y 1 ) .

В том случае, когда a x = 0 , каноническое уравнение прямой принимает вид x — x 1 0 = y — y 1 a y и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.

Каноническое уравнение прямой при условии, что a y = 0 , принимает вид x — x 1 a x = y — y 1 0 . Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.

Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.

Параметрические уравнения прямой на плоскости

Данные уравнения имеют вид x = x 1 + a x · λ y = y 1 + a y · λ , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.

Назначение параметрического уравнения в том, чтобы установить неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .

Числа x , y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .

Предположим, что λ = 0 .

Тогда x = x 1 + a x · 0 y = y 1 + a y · 0 ⇔ x = x 1 y = y 1 , т. е. точка с координатами ( x 1 , y 1 ) принадлежит прямой.

Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.

Рассмотрим параметрические уравнения прямой линии вида x = 2 + 3 · λ y = 3 + λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку ( x 1 , y 1 ) и имеет направляющий вектор a → = ( 3 , 1 ) .

Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».

Нормальное уравнение прямой

Нормальное уравнение прямой имеет вид , A x + B y + C = 0 , где числа А , В , и C таковы, что длина вектора n → = ( A , B ) равна единице, а C ≤ 0 .

Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат O х у , является вектор n → = ( A , B ) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n → = ( A , B ) .

Еще одним вариантом записи нормального уравнения прямой линии является cos α · x + cos β · y — p = 0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n → = ( cos α , cos β ) , справедливо равенство n → = cos 2 α + cos 2 β = 1 , величина p ≥ 0 и равна расстоянию от начала координат до прямой.

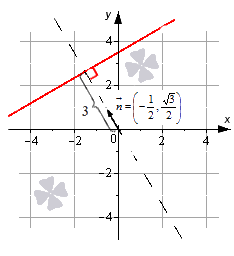
Рассмотрим общее уравнение прямой — 1 2 · x + 3 2 · y — 3 = 0 . Это общее уравнение прямой является нормальным уравнением прямой, так как n → = A 2 + B 2 = — 1 2 2 + 3 2 = 1 и C = — 3 ≤ 0 .

Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты — 1 2 , 3 2 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n → = — 1 2 , 3 2 .

Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.

Если в общем уравнении прямой A x + B y + C = 0 числа А , В и С таковы, что уравнение A x + B y + C = 0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».

Контрольная работа по мат. анализу 06

Элементы векторной алгебры и аналитической геометрии

Контрольная работа 1

1. Даны координаты вершин пирамиды. Найти: 1) длину рёбер А1А2 и А1А3; 2) Угол между рёбрами А1А2 и А1А3; 3) Площадь грани А1А2А3; 4) Объём пирамиды; 5) Уравнение прямой А1А2; 6) Уравнение плоскости А1А2А3; 7) Угол между ребром А1А4 и гранью А1А2А3; 8) Уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Координаты вершин: А1(5;1;0), А2 (0;1;2), А3(3;0;1), А4(2;2;2).

Координаты векторов находим по формуле: X = xj — xi; Y = yj — yi; Z = zj — zi

Здесь X, Y,Z координаты вектора; xi, yi, zi — координаты точки Аi; xj, yj, zj — координаты точки Аj; Для вектора A1A2 : X = x2 — x1; Y = y2 — y1; Z = z2 — z1

X = 0-5; Y = 1-1; Z = 2-0

1) Длина рёбер А1А2 и А1А3;

Длина вектора a(X;Y;Z) выражается через его координаты формулой:

2) Угол между рёбрами А1А2 и А1А3;

Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:

, где a1a2 = X1X2 + Y1Y2 + Z1Z2

Найдем угол между ребрами A1A2 и A1A3

, γ = arccos(0.91) = 24.50

3) Площадь грани А1А2А3;

Найдем площадь грани с учётом геометрического смысла векторного произведения:

4) Объём пирамиды;

Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:

Находим Определитель матрицы

∆ = (-5) • ((-1) • 2-1 • 1)-(-2) • (0 • 2-1 • 2)+(-3) • (0 • 1-(-1) • 2) = 5

5) Уравнение прямой А1А2;

Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:

Уравнение прямой A1A2

6) Уравнение плоскости А1А2А3;

Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

Уравнение плоскости A1A2A3

(x-5)(0 • 1-(-1) • 2) — (y-1)((-5) • 1-(-2) • 2) + (z-0)((-5) • (-1)-(-2) • 0) = 2x+y+5z-11=0

7) Угол между ребром А1А4 и гранью А1А2А3;

Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле

8) Уравнение высоты, опущенной из вершины А4 на грань А1А2А3.

Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:

2. Линия задана уравнением В полярной системе координат

1. построить линию по точкам, начиная от До И придавая значения через промежуток ;

2. найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью;

3. по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

1) Построим линию по точкам, начиная от До и придавая Значения через промежуток

2) Построим уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.

3) Найдём уравнение данной линии в декартовой системе координат:

Используем формулы перехода от полярной системы координат к декартовой:

Тогда

По уравнению в декартовой прямоугольной системе координат определяем, что это линия — гипербола.

Элементы линейной алгебры

Контрольная работа 2

I. Даны две матрицы А и В. Найти (2АТ-3В)*(А+2ВТ)

, ,

II. Определить собственные значения и собственные векторы матрицы третьего порядка.

Исходная матрица имеет вид:

Составляем систему для определения координат собственных векторов:

(5 — λ)x1-2×2 + 2×3 = 0

0x1 + (5 — λ)x2 + 0x3 = 0

0x1 + 2×2 + (3 — λ)x3 = 0

Составляем характеристическое уравнение и решаем его.

Для этого находим определитель матрицы и приравниваем полученное выражение к нулю.

(5 — λ) • ((5 — λ) • (3 — λ)-2 • 0)-0 • (-2 • (3 — λ)-2 • 2)+0 • (-2 • 0-(5 — λ) • 2) = 0

После преобразований, получаем: — λ3 + 13λ2 — 55λ + 75 = 0

Один из корней уравнения равен λ1 = 3

Тогда характеристическое уравнение можно записать как

(λ -3)( — λ2 + 10λ — 25)=0.

D = 102 — 4 • (-1) • (-25) = 0

Получили собственные числа: λ1 = 3,

Найдём собственный вектор для λ1.

Составляем систему для определения координат собственных векторов:

Подставляя λ = 3 в систему, имеем:

Пусть x1 — свободное неизвестное, тогда выразим через него все остальные x1.

Множество собственных векторов, отвечающих собственному числу λ1= 3 , имеет вид: , где x1 — любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x1 = 1: .

Рассуждая аналогично, находим собственный вектор, отвечающий собственным числам:

. Следовательно, — любое,

Множество собственных векторов, отвечающих собственным числам , имеет вид: . При x1 = 1 и x3 = 0: , при x1 = 0 и x3 = 1: .

Ответ: Собственные числа: λ1=3, , собственные векторы: , , .

III. Дано комплексное число z. Требуется: 1) записать число z в алгебраической и тригонометрической формах; 2) Найти все корни уравнения w3+z=0

1) — алгебраическая форма

— тригонометрическая форма

2) Найдем корни уравнения w3 =0,

Применим формулу извлечения корней из комплексного числа:

, к=0,1,…,n-1

Так как a=, то

Контрольная работа 3

I. Найти пределы функций, не пользуясь правилом Лопиталя.

Использовали эквивалентности бесконечно малых величин при :

II. Задана функция . Найти точки разрыва функции, если они существуют. Сделать чертёж

Построим график заданной функции:

Функция определена на всём множестве чисел и неэлементарная.

Каждая из составляющих функций непрерывна на своём промежутке; заданная функция может иметь точки разрыва только в точках смены аналитических выражений, то есть в точках и .