Логарифмические уравнения и неравенства
Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
Логарифмическая функция
Определение
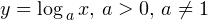
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:
| | a > 1 | 0 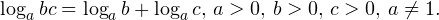 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/> 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:
• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):
Решение логарифмических уравнений и неравенствПример 1. Решите уравнение: Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:
С учетом того, что получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения: На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению: В область допустимых значений входит только первый корень. Ответ: x = 7. Пример 2. Решите уравнение: Решение. Область допустимых значений уравнения определяется системой неравенств:
Очевидно, что эти два условия противоречат друг другу. То есть нет ни одного такого значения x, при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет. Ответ: корней нет. Обратите внимание, что в этом задании нам вообще не пришлось искать корни уравнения. Достаточно оказалось определить, что его область допустимых значений не содержит ни одного действительно числа. Это одно из преимуществ такой последовательности решения логарифмических уравнений и неравенств (начинать с определения области допустимых значений уравнения, а затем решать его путем равносильных преобразований). Примет 3. Решите уравнение: Решение. Область допустимых значений уравнения определяется здесь легко: x > 0. Уравнение принимает вид: Оба ответа входят в область допустимых значений уравнения, поскольку являются положительными числами. Пример 4. Решите уравнение: Решение. Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению: Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению: Первый корень не входит в область допустимых значений уравнения, второй — входит. Ответ: x = -1. Пример 5. Решите уравнение: Решение. Будем искать решения в промежутке x > 0, x≠1. Преобразуем уравнение к равносильному: Оба ответа входят в область допустимых значений уравнения. Пример 6. Решите уравнение: Решение. Система неравенств, определяющая область допустимых значений уравнения, имеет на этот раз вид: Используя свойства логарифма, преобразуем уравнение к равносильному в области допустимых значений уравнению: Используя формулу перехода к новому основанию логарифма, получаем: В область допустимых значений входит только один ответ: x = 4. Перейдем теперь к логарифмическим неравенствам. Это как раз то, с чем вам придется иметь дело на ЕГЭ по математике. Для решения дальнейших примеров нам потребуется следующая теорема: Теорема 2. Если f(x) > 0 и g(x) > 0, то: Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству: Окончательно, с учетом области допустимых значений получаем ответ: Пример 8. Решите неравенство: Решение. Вновь начнем с определения области допустимых значений:
На множестве допустимых значений неравенства проводим равносильные преобразования: После сокращения и перехода к равносильному по теореме 2 неравенству получаем: С учетом области допустимых значений получаем окончательный ответ: Пример 9. Решите логарифмическое неравенство: Решение. Область допустимых значений неравенства определяется следующей системой:
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству: С учетом области допустимых значений получаем окончательный ответ: Пример 10. Решите неравенство: Решение. Область допустимых значений неравенства определяется системой неравенств:
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству: Неравенство будет равносильно двум системам. Первой: Итак, окончательный ответ: II способ. Решаем методом интервалов. Преобразуем неравенство к виду: Вычтем из знаменателя С учетом того, что выражения Множество решений данного неравенства Итак, Итак, что нужно для того, чтобы решать логарифмические уравнения и неравенства?
Главное же требование — это настойчивость в достижении своей цели. Учитесь, тренируйтесь, если нужно — ежедневно, изучайте и запоминайте на примерах основные способы решения неравенств и их систем, анализируйте возникающие ошибки и не допускайте их в будущем. За помощью в этом нелегком деле вы можете обратиться к своему школьному учителю по математике, репетитору, родителям, друзьям и знакомым, книгам, а также огромному количеству материалов, доступных на просторах Интернета. Желаю вам успехов в подготовке к Единому государственному экзамену по математике. АлгебраПлан урока: Задание. Укажите корень логарифмического уравнения Задание. Решите урав-ние В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид Задание. Найдите решение логарифмического уравнения Задание. Решите урав-ние Задание. Решите урав-ние Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания: Уравнения вида logaf(x) = logag(x)Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов. Задание. Решите урав-ние Задание. Найдите корень урав-ния Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями. Задание. Решите урав-ние Получили квадратное уравнение, которое решаем с помощью дискриминанта: Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем: Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4: Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log3 (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3). Уравнения, требующие предварительных преобразованийЕстественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду logaf(x) = logag(x). Задание. Решите урав-ние с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае: Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы: Задание. Решите урав-ние Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем Задание. Решите урав-ние Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log5 5. Тогда урав-ние можно преобразовать: Задание. Решите урав-ние Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что Задание. Решите урав-ние Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log25x 4 к основанию 5, используя известную нам формулу Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы: Логарифмические уравнения с заменой переменныхИногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид. Задание. Решите уравнение методом замены переменной Задание. Найдите решение уравнения методом замены переменной Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части: Логарифмирование уравненийЯсно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры. Задание. Укажите корни урав-ния Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5: Возвращаемся от переменной t к переменной х: Переход от логарифмических неравенств к нелогарифмическимРассмотрим график логарифмической функции у = logax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными. Задание. Найдите решение логарифмического неравенства Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 logas: Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 loga s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения: Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5). Урок по математике «Логарифмы и их свойства. Логарифмическая функция. Логарифмические уравнения и неравенства»Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. «Актуальность создания школьных служб примирения/медиации в образовательных организациях» Свидетельство и скидка на обучение каждому участнику Выберите документ из архива для просмотра:Выбранный для просмотра документ Открытый урок.ppt Описание презентации по отдельным слайдам:Есть в математике тема одна, Логарифмы называется она, Логарифм появился, чтобы легче считать, Логарифм – ПОКАЗАТЕЛЬ, Это надо знать! повторить и запомнить определения и свойства логарифма и логарифмической функции познакомиться с историей логарифмов и их использованием в деятельности человека и в природе применять полученные знания при выполнении практических заданий проверять правильность полученных решений Разминка 1. Дайте определение логарифма числа по заданному основанию Ответ: Разминка 2. Сформулируйте основное логарифмическое тождество Ответ: Разминка 3. Чему равен логарифм 1? Ответ: Разминка 4. Чему равен логарифм числа a по тому же основанию a? Ответ: Разминка 5. Чему равен логарифм произведения? Ответ: Разминка 6. Чему равен логарифм частного? Ответ: Разминка 7. Чему равен логарифм степени? Ответ: Разминка 8. Какова область определения логарифмической функции Ответ: Разминка 9. Какова область значений логарифмической функции Ответ: Разминка 10. При каком условии функция является монотонно-возрастающей? Ответ: при функция монотонно-возрастает Разминка 11. При каком условии функция является монотонно-убывающей? Ответ: при функция монотонно-убываетает. Диктант «Проверь себя» Найти х: Диктант «Проверь себя» Найти х: Диктант «Проверь себя» Вычислить: Диктант «Проверь себя» Вычислить: Диктант «Проверь себя» Вычислить: Диктант «Проверь себя» Вычислить: Диктант «Проверь себя» Вычислить: Диктант «Проверь себя» Вычислить: Диктант «Проверь себя» Вычислить: Ответы к диктанту Джон Непер Е – 100Ж – 2П – 1О – 3 Н – -1 Д – 1/3Р — 0К – -3А – 4 Л – -10 Шотландский математик – изобретатель логарифмов. В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый труд “Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году. Ему принадлежит определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии. Джон Непер (Шотландия, 16-17вв.) Русский математик Аничков Д. С. о логарифмах «Ежели под геометрическою прогрессиею, начинающуюся с единицы, подписана будет арифметическая прогрессия, начинающаяся с нуля, то числа, внизу подписанные, называются для верхних – логарифмы. Положим, что даны прогрессии: геометрическая 1, 2, 4, 8, 16, 32, 64, 128, 256, арифметическая 0, 1, 2, 3, 4, 5, 6, 7, 8. Тогда логарифм 1 будет 0; логарифм 4 будет 2; а логарифм 32 будет 5 и проч.» ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА Логарифмы очень упрощают деление и умножение. Например, для умножения двух чисел складывают их логарифмы, результат находят в таблице логарифмов. В дальнейшем Д. Непером была изобретена логарифмическая линейка, которой пользовались до 70-х годов нашего века. Логарифм в музыке в шумах и звуках Логарифмическая спираль Логарифмическую спираль можно увидеть на рис.1. Спираль в одну сторону развертывается до бесконечности, а вокруг полюса, напротив, закручивается, стремясь к нему, но не достигая. Так почему в качестве примера логарифмической зависимости в природе выбрали именно логарифмическую спираль? и в природе улитка клюв семечки подсолнуха паутина рога горного барана По логарифмической спирали формируется и тело циклона ЗАПОМНИ ! Сладкая парочка! Два в одном! Два берега у одной реки! Два сапога – пара! Близки и неразлучны! Нам не жить друг без друга! Логарифм и ОДЗ вместе трудятся везде! ОН — ЛОГАРИФМ! ОНА — ОДЗ! Кто быстрее Укажите ОДЗ данного логарифмического выражения Сверь ответ 1. 2. 3. «Смотри не ошибись» Решить логарифмические уравнения 1. 2. 3. 4. 5. Ответы 1. 2. ОДЗ: х = -10 ∉ ОДЗ ⇒ корней нет Ответы 3. замена обратная замена: 4. ОДЗ: Ответы 5. Критерий оценок: «3» — если решили верно три примера; «4» — если решили верно четыре примера; «5» — если решили верно пять примеров Докажем, что 2 > 3 Очевидно, что 1/4 > 1/8 ● После приведения к основанию ½: ( ½ )2 > ( ½ )3 ● После логарифмирования по основанию 10: lg ( ½ )2 > lg ( ½ )3 ● По свойству логарифмов: 2 lg ( ½ ) > 3 lg ( ½ ) ● После сокращения на lg ( ½ ): 2 > 3 В чём ошибка? 2 > 3 ?! «Свойства логарифмической функции» Логарифмическая функция определена при любом значении аргумента «Свойства логарифмической функции» Для логарифмической функции основание «Свойства логарифмической функции» Областью определения является множество всех действительных чисел «Свойства логарифмической функции» Областью значения является множество действительных чисел «Свойства логарифмической функции» Функция монотонно-возрастающая «Свойства логарифмической функции» Логарифмическая функция имеет экстремум в точке (1;0) «Свойства логарифмической функции» График логарифмической функции пересекает ось ОХ «Свойства логарифмической функции» График логарифмической функции расположен в верхней полуплоскости «Свойства логарифмической функции» График логарифмической функции симметричен относительно оси ОХ «Свойства логарифмической функции» График логарифмической функции проходит через начало координат Ответы -;+; -; +; +; -; +; -; -; — Выставь себе оценку: «3» – 6-7 правильных ответов; «4» – 8-9 правильных ответов; «5» – 10 правильных ответов СВОЙСТВА И ГРАФИК ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ Ответ: №4 НА ОДНОМ ИЗ РИСУНКОВ ИЗОБРАЖЕН ГРАФИК ФУНКЦИИ . УКАЖИТЕ НОМЕР ЭТОГО РИСУНКА y = log2x Совпадают ли графики функций Ответ: нет, т.к. D(y1)≠D(y2) Домашнее задание 1. Найти область определения функции Домашнее задание 2. Решите уравнения (графически) Домашнее задание 3. Решите неравенства Итог занятия: повторили определение и основные свойства логарифма; использовали их при решении заданий, встречающихся в зачетной работе по теме и на экзамене; познакомились с создателем логарифмов – Д. Непером; узнали, где можно встретиться с логарифмами. Значимость логарифмов «С точки зрения вычислительной практики, изобретение логарифмов по важности можно смело поставить рядом с другим, более древним великим изобретением индусов – нашей десятичной системой нумерации». Успенский Я. В., русский математик Выбранный для просмотра документ Открытыйурок.docx ТЕМА: «Логарифмы и их свойства. Логарифмическая функция. Логарифмические уравнения и неравенства». Цели: 1. Повторить теоретический материал, проверить, откорректировать и закрепить знания учащихся о свойствах логарифмов и логарифмической функции, в решении уравнений и неравенств. 2. Способствовать развитию мышления, речи, внимания, памяти. 3. Воспитывать настойчивость и упорство в достижении цели, содействовать воспитанию интереса к предмету. Тип занятия : Проверка, оценка, коррекция знаний, умений, навыков. Оргмомент. (3 мин.) I этап. Разминка: устная проверка знаний теоретического материала (7 мин) II этап. Математический диктант «Проверь себя» (8 мин). III этап Историческая справка. Логарифмы в жизни человека и в природе.(10 мин) IV этап. Кто быстрее: «Указать ОДЗ данного логарифмического выражения» (5-7 м) V этап Дифференцированная самостоятельная работа «Смотри не ошибись» (15 м) VI этап Софизм. Доказательство неравенства 2 > 3.(3 мин) VII этап Математический диктант «Свойства логарифмической функции», проверка, вопросы. (10 мин) Домашнее задание (3 мин) Итог занятия (3 мин) Игра Математический футбол «Логарифм в мешке» (10 мин) 1. (3 мин) Оргмомент. ( слайд) Есть в математике тема одна, логарифмической функцией называется она. Логарифм появился, чтобы легче считать, Логарифм — п о к а з а т е л ь , это надо знать! Сегодня на уроке мы повторим теоретический материал по теме «Логарифмы» и проведем подготовку к зачетной работе. (слайд ) Цели занятия: — повторить и запомнить определения и свойства логарифма и логарифмической функции; — применять полученные знания при выполнении практических заданий; — проверять правильность полученных решений; — познакомиться с историей логарифмов и их использованием в деятельности человека и в природе. Сегодняшнее наше занятие построено по этапам. 2. (7 мин) I этап Разминка ( устная проверка знаний теоретического материала) (слайды) 1. Дайте определение логарифма числа по заданному основанию. Ответ: 2. Сформулируйте основное логарифмическое тождество. Ответ: 3. Чему равен логарифм 1? Ответ: 4. Чему равен логарифм числа a по тому же основанию a ? Ответ: 5. Чему равен логарифм произведения? Ответ: 6. Чему равен логарифм частного? Ответ: 7. Чему равен логарифм степени? Ответ: 8. Какова область определения логарифмической функции Ответ: 9. Какова область значений логарифмической функции Ответ: 10. При каком условии функция Ответ: при 11. При каком условии функция Ответ: при 3. (8 мин) II этап Диктант «Проверь себя». (слайды) 1. 3. Вычислить: 4. Вычислить: 5. Вычислить: 6. Вычислить: 7. Вычислить: 8. Вычислить: 9. Вычислить: (ответы: 1/3; 2; 3; -1; -1; 100; 1; 100;0 ) ( слайд) Выпишите по порядку буквы, которые соответствуют вашим ответам и прочитайте, что у вас получилось: (слайды) Джону Неперу принадлежит сам термин «Логарифм», который он перевел как «Искусственное число». Этот термин был введен в 1594 году. Джон Непер-шотландец. В 16 лет отправился на континент, где в течении 5 лет в университете изучал математику, физику, астрономию. В своей дальнейшей жизни Непер серьезно не занимался математикой и астрономией. Имел свое имение, занимался земледелием и изобретением приборов. К идее логарифмических вычислений Непер пришел еще в 80-х годах XVI века, однако опубликовал свои таблицы только в 1614 году, после 25-летних вычислений. Они вышли под названием «Описание чудесных логарифмических таблиц». Логарифмы позволили перейти от сложных действий: возведение в степень, извлечение корня к умножению и делению, а затем к сложению и вычитанию. (слайды) Применение логарифмов на эстраде, в музыке, в технике, в природе. Логарифмическая спираль. 5. (5-7 мин) IV этап Кто быстрее. Выполнение различных примеров с логарифмическими выражениями неотъемлемо связано с нахождением Чего? (слайд) Укажите ОДЗ данного логарифмического выражения 1. 2. 3. ( c лайд 10 – ответы: 1. ОДЗ: 2. ОДЗ: 3. ОДЗ: 6. (15 мин) V этап «Смотри не ошибись». Дифференцированная самостоятельная работа. ( слайды) Решить логарифмические уравнения. Время 15 минут. 1. 2. 3. 4. 5. (уравнения решают в тетради, полученные ответы выписывают на листок и сдают на проверку; ответы сверяют и выставляют себе оценку) (слайд) ответы и критерий оценок) Ответы: 1. 2. ОДЗ: 3. замена обратная замена: 4 . ОДЗ: 5. Критерий оценок: «3» — если решили верно три примера; «4» — если решили верно четыре примера; «5» — если решили верно пять примеров. 7. (3 мин) VI этап Найди ошибку в доказательстве неравенства «2 8. (10 мин) VII этап. Диктант «Свойства логарифмической функции» Вспомните основные свойства логарифмической функции и ответьте на вопросы. На вопросы задания отвечаем только «да» (+) или «нет» (-) 1. Логарифмическая функция 2. Для логарифмической функции 3. Областью определения является множество всех действительных чисел. 4. Областью значения является множество действительных чисел. 5. Функция 6. Логарифмическая функция имеет экстремум в точке (1;0). 7. График логарифмической функции пересекает ось ОХ. 8.График логарифмической функции расположен в верхней полуплоскости. 9. График логарифмической функции симметричен относительно оси ОХ. 10. График логарифмической функции проходит через начало координат. Выпишите свои ответы на листочек и сдайте. Записи в тетради сверьте с ответами на доске. Выставьте себе оценку: «3» — 6-7 правильных ответов, «4» -8-9 правильных ответов, «5» — 10 правильных ответов. 9. ( 3 мин) Домашнее задание: подготовиться к зачетной работе; Выполнить задания: (слайд) 1 Найти область определения функции 2. Решить уравнения 3. Решить неравенства 10. (3 мин) Итог урока (слайд) Подведем итог занятия. Мы с вами сегодня Повторили определение и основные свойства логарифма; Использовали их при решении заданий, встречающихся в зачетной работе по теме и на экзамене; Познакомились с создателем логарифмов — Джоном Непером; Узнали, где встречаются логарифмы. Значимость логарифмов — высказывание Я.В.Успенского. 11. (10 мин) Игра Математический футбол «Логарифм в мешке» ( слайды) В оставшееся время мы с вами немного поиграем. Эта игра – математический футбол: вам предлагается выбрать, кто будет отвечать на вопрос. Слово логарифм состоит из двух частей логос – отношение и аритмос – число. Переводится на русский язык « число, измеряющее отношение» Выбор такого названия объясняется тем, что логарифмы возникли при сопоставлении двух чисел, одно из которых является членом геометрической прогрессии, а другое – членом арифметической прогрессии. В музыке играя по клавишам современного рояля, музыкант не знает, что он играет на логарифмах. Номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков. Номер октавы представляет собой целую часть (характеристику), а номер звука в данной октаве – дробную часть (мантиссу) этого логарифма. В звуках и шумах громкость звука и шума оценивается по логарифмической шкале. Вредное влияние промышленных шумов на здоровье рабочих и на производительность труда побудило выработать приемы точной оценки громкости шума. Единицей громкости служит « бел». Последовательные степени громкости – 1 бел, 2 бела и т.д. составляют для нашего слуха арифметическую прогрессию. Физическая же «сила» этих шумов составляет геометрическую последовательность со знаменателем 10. Поэтому громкость шума, выраженная в белах, равна десятичному логарифму его физической силы. К слову, шелест листьев оценивается в 1 бел, громкая разговорная речь – 6,5 бела. Шум, громкость которого больше 8 белов, признается вредной для человеческого организма. Удар молотка о стальную плиту оценивается в 11 бел. При измерении шума имеют дело с логарифмической зависимостью между величиной ощущения и порождающего его раздражения : величина ощущения пропорциональна логарифму величины раздражения. Логарифмическая спираль: впервые о логарифмической спирали упоминается в 1638 году Рене Декартом. Одно из замечательных свойств логарифмической спирали состоит в том, что произвольный луч, выходящий из ее полюса, пересекает любой виток спирали под одним и тем же углом. Это свойство применяется в режущих машинах, в частности – в мясорубке. Трубу, подводящую струю воды к лопастям турбинного колеса на гидроэлектростанции следует заворачивать по логарифмической спирали. Тогда потери энергии движущейся воды будут минимальными. Безобидная воронка, образованная вытекающей из ванны водой; свирепый смерч, опустошающий все на своем пути; величественный круговорот гигантского космического вихря туманностей и галактик – все они имеют форму спирали. Семена в корзине подсолнуха, паутина паука , раковина улитки, клюв некоторых птиц, рога горного барана располагаются по кривым, близким к дугам логарифмической спирали. Краткое описание документа:«Описание материала: Данный урок проводился на первом курсе в Соликамском » автомобильно-дорожном колледже после изучения темы: «Логарифмы. Логарифмическая функция, ее свойства. Логарифмические уравнения и неравества». Цель проведения данного занятия: обобщить, систематизировать изученный материал по данной теме; расширить представления об использовании логарифмов в других сферах; развивать вычислительные навыки. Каждый этап занятия отражается на слайдах презентации. Пустой слайд презентации — переход от одного этапа к другому. Разработку данного занятия можно применять в школе на уроках алгебры в 11 классе в конце изучения данной темы и при подготовке к ЕГЭ. источники: http://100urokov.ru/predmety/urok-9-uravneniya-logarifmicheskie http://infourok.ru/material.html?mid=31119 |
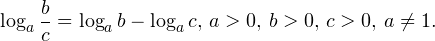 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>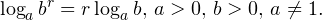 0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>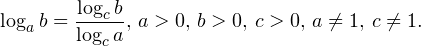 0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>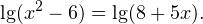
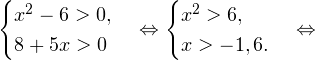 0, \\ 8+5x > 0 \end
0, \\ 8+5x > 0 \end 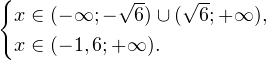
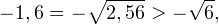 -\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>
-\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>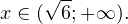
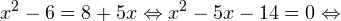
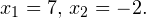
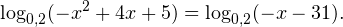
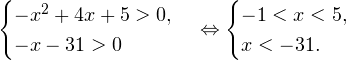 0, \\ -x-31>0 \end
0, \\ -x-31>0 \end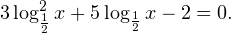
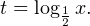
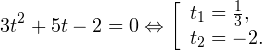
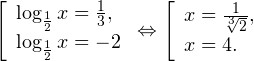
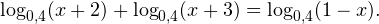
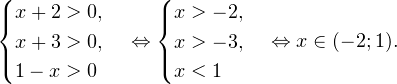 0, \\ x+3>0, \\ 1-x>0 \end
0, \\ x+3>0, \\ 1-x>0 \end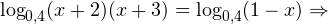
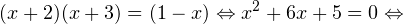
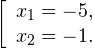
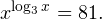
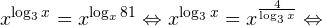
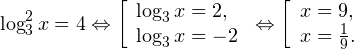
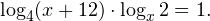
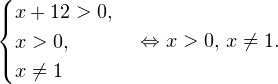 0, \\ x>0, \\ x\ne 1 \end
0, \\ x>0, \\ x\ne 1 \end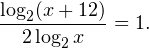
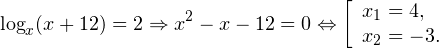
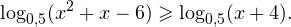
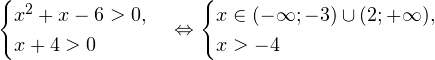 0, \\ x+4>0 \end
0, \\ x+4>0 \end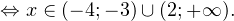
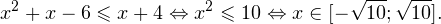
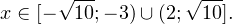
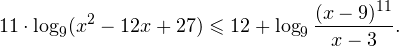
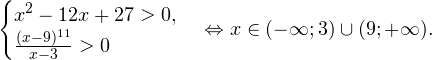 0, \\ \frac<(x-9)^<11>>
0, \\ \frac<(x-9)^<11>>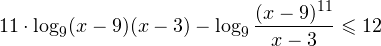
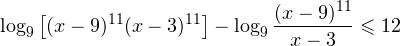
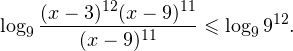
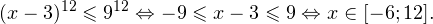
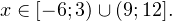
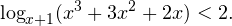
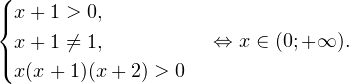 0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end
0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end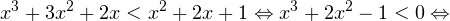
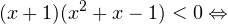
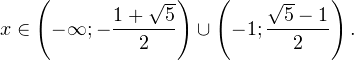
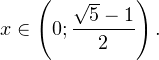
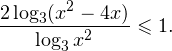
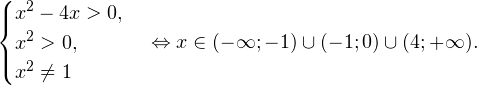 0, \\ x^2>0, \\ x^2\ne 1 \end
0, \\ x^2>0, \\ x^2\ne 1 \end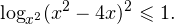
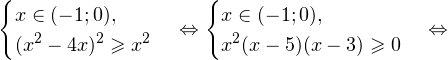
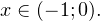
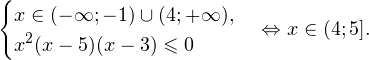
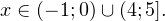
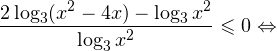
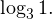 Это ничего не изменит, поскольку
Это ничего не изменит, поскольку 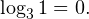
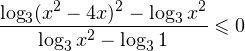
 и
и  — одного знака при
— одного знака при 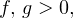 0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход:
0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход: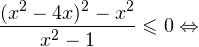
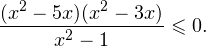
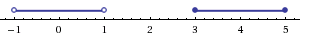
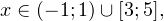 а с учетом области допустимых значений получаем тот же результат:
а с учетом области допустимых значений получаем тот же результат: 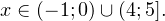









 ?
?

 функция монотонно-возрастает.
функция монотонно-возрастает. функция монотонно-убываетает.
функция монотонно-убываетает. . Найти
. Найти  .
. .
.  Найти
Найти  .
. .
. .
. .
. .
. .
.




















 .
. »
» .
. монотонно-возрастающая.
монотонно-возрастающая.




